Journal of Computer and Communications
Vol.06 No.11(2018), Article ID:88464,11 pages
10.4236/jcc.2018.611005
An Image Enhancement Method Based on Fractional Calculus and Retinex
Jingang Cao
School of Control and Computer Engineering, North China Electric Power University, Baoding, China
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 21, 2018; Accepted: November 11, 2018; Published: November 14, 2018
ABSTRACT
In order to resolve the problem of the image degradation, an image enhancement method based on fractional calculus and Retinex is proposed, which can preserve or enhance texture information and remove the noise of images. The fractional differential is used to preprocess the input image to enhance texture information, and using guided filter to estimate the illumination component, so it has less halo phenomena. The reflection component, obtained according to the Retinex theory, is denoised by fractional integral to remove the noises. The image is equalized by the contrast limited adaptive histogram equalization to improve the image contrast, and a final enhanced image is obtained. The experimental results show that the method can effectively achieve image enhancement, and the enhanced image has better visual effects.
Keywords:
Fractional Calculus, Retinex, Guided Filter, Image Enhancement

1. Introduction
With the acceleration of the digitalization process, digital images have gradually been applied to many fields, such as medical, transportation, monitoring and detection, et al. However, due to environmental and equipment conditions, the captured image will be degraded and distorted, and image enhancement can improve image quality and enrich image information, which is beneficial to further image processing. There are many methods for image enhancement, such as histogram equalization, Retinex, wavelet transform, dark channel prior, and so on.
Image enhancement methods based on Retinex theory are more common. The key is how to estimate the illumination component. Gaussian filtering is usually used to estimate the illumination component. Retinex-based image enhancement methods include single-scale Retinex (SSR) [1] , multi-scale Retinex (MSR) [2] , and color-recovery multi-scale Retinex (MSRCR) [3] . SSR is mainly used to enhance grayscale images. MSR and MSRCR are used for color image enhancement, but enhanced images have color distortion and halo artifacts. Researchers have done a lot of research on Retinex theory. In [4] , a method combines dark channel prior and Retinex theory to achieve fast defogging of a single image; In [5] , authors use improved fractional differential operators and depth of field measurements of Retinex to enhance images; In [6] , fractional differential, dark primary a priori and Retinex method is proposed to dehaze images; In [7] , authors use Retinex method based on iterative multi-scale guided filtering to enhance low-light images. Although these improvement methods have achieved certain effective, they are all for a specific scene.
The paper proposes an image enhancement method based on fractional calculus and Retinex. The method firstly uses the fractional differential to preprocess the image, and then based on the single-scale Retinex algorithm, uses the guided filter [8] to estimate the illumination component and remove it, thereby obtaining the reflection component, then using fractional integral to denoise and obtain the enhanced image.
2. Related Theory
2.1. Fractional Calculus
Fractional calculus is generalization of classical calculus, the order of fractional calculus can be an arbitrary order. According to the application of fractional calculus in digital images, fractional differential has the ability to detect blurred boundary and weak texture of images, and fractional integration can denoise the image [9] [10] .
For an arbitrary square integrable energy signal , the v-order fractional derivative is , , and its Fourier transform:
(1)
In the formula (1), is called v-order differential multiplier function, and its exponential form:
(2)
Thereby, the amplitude-frequency characteristic curve of the fractional calculus shown in Figure 1.
Figure 1(a) is the amplitude-frequency characteristic curve of fractional differential, and Figure 1(b) is the amplitude-frequency characteristic curve of fractional integral. 0 < w < 1 is a low-frequency portion, and w > 1 is a high-frequency portion. The texture detail of the two-dimensional image does not change significantly in the low frequency region, while the gray level in the high frequency region changes drastically or the high frequency region is the edge portion of the image. It can be seen from Figure 1 that when v > 0, the differential operation is realized, which is equivalent to a high-pass filter. The high frequency of the image is strengthened, and the low-frequency information is nonlinearly retained to a certain extent, which is advantageous for highlighting the local detail of the image. So fractional differential can enhance edges and texture of the image. When v < 0, the integral operation is realized, which is equivalent to low-pass filter, and can enhance the low frequency of the image and suppress high frequency information, that is, after the fractional integral, the noise can be removed and the details of the edge and texture of the image can be preserved to a certain extent. When v = 0, it is an all-pass filter.


Figure 1. Amplitude-frequency characteristic curve of the fractional calculus. (a) Fractional differential; (b) Fractional integral.
2.2. Retinex Theory
The Retinex theory, proposed by Edwin H. Land [11] , is based on the behavior of human visual system. The Retinex algorithm is an image enhancement method based on color constancy. In the Retinex algorithm, the input image I consists of the illumination component L and the reflection component R, i.e., I = L·R, as shown in Figure 2. To enhance the image with Retinex, it is necessary to first estimate the illumination component L from the input image I. And then discard the estimated illumination from the input image to obtain the reflection component, so the effect of nonuniform lighting can be removed and the visual effect of the image can be improved. In the specific implementation, the image is usually transformed to a logarithm domain, i.e.,
,
then the enhanced image can be obtained by inverse logarithm transform.
3. The Proposed Algorithm
3.1. Fractional Calculus Mask Structure
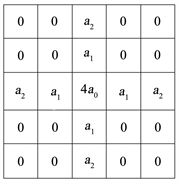
Using fractional calculus to process images, one of the key is the design of fractional calculus mask operator. Commonly, the size of fractional differential mask is (2n + 1) × (2n + 1), n is a positive integer, and Tiansi operator [9] is one of classical fractional differential masks, as shown in Figure 3. The non-zero elements of Tiansi operator are determined by the coefficients of fractional differential expression, which is defined as follow [10] :
(3)
so, , , . Tiansi operator has anti-rotation capability and fractional calculus have 8 directions of negative and positive x-coordinate,
negative and positive y-coordinate, left and right upward diagonal, left and right downward diagonal. When using Tiansi operator to improve an image, there will have white lines on the image edges. In order to eliminate the white edge, a fractional calculus mask operator is redesigned. According to the Laplacian operator, the fractional differential is introduced and extended to a 5 × 5 fractional differential mask operator, which structure is shown in Figure 4, , and is the same as Tiansi operator.
3.2. The Proposed Algorithm
Figure 5 is the flow of image enhancement processing, which combines fractional calculus and Retinex.
The processing steps of the proposed algorithm are as follows:
Figure 2. Retinex theory.
Figure 3. 5 × 5 Tiansi operator.
Figure 4. The proposed operator.
Figure 5. The flow of the proposed algorithm.
1) The original image is preprocessed by the fractional differential, which can enhance the edge of the image and also can enhance the weak texture nonlinearly.
2) Estimate illumination component of the image according to the guided filter.
3) According to the single-scale Retinex algorithm, the preprocessed image is divided by the illumination component to obtain the reflection component.
4) Denoise the image by a fractional integral on the reflected component.
5) Improve the contrast by contrast-limited adaptive histogram equalization and get the final enhanced image.
4. Experiment Simulation and Results Analysis
In order to verify the effectiveness of the proposed algorithm, Histogram equalization (HE), fractional differential (FD), single-scale Retinex algorithm (SSR), multi-scale Retinex algorithm (MSR), fractional differential combined with single-scale Retinex algorithm (FDSSR) and the proposed algorithms are used to enhance images. The experiment environment is as follows: the operating system is Windows 7, the simulation software is MATLAB R2014b, the processor is Intel (R) Core (TM) i5-6500, and the memory is 4 GB.
In the experiment, FD and FDSSR adopt Tiansi operator, and the order of fractional differential is 0.5. The order of fractional calculus in the proposed algorithm is 0.2 and −0.2, respectively. Figure 6 shows original images and enhanced images. 1) is the image of building, 2) is the image of people, 3) is the image of lena and 4) is the image of barche. The effect of image enhancement is evaluated subjectively and objectively. The subjective evaluation is based on the visual effect of images. The objective evaluation has no unified standard at present, and it is mainly based on some information of images.
According to the visual effect of images of each group in Figure 6, it can be seen that HE has the largest contrast, the black and white is more distinct, but the image details are not enough. FD and FDSSR have small contrast, the visual effect is dark, and the enhancement is not obvious. Distortion occurs in the enhanced images of MSR. Compared with SSR, the proposed algorithm has the best visual effect and the most abundant image details.
In order to evaluate the effect of enhanced images objectively, the average gradient, the information entropy, the gray mean and the standard deviation are used to make a comprehensive evaluation. Assuming the size of the image is .
1) Average gradient: The average gradient of the image reflects the sharpness and texture change of an image. Generally, the larger the average gradient is, the clearer the image details has. A high average gradient also means the better edge preservation effect of an image, but the increase of noise will increase the average gradient. The average gradient is defined as
(4)
where is the horizontal gradient, and is the vertical gradient.
2) Information entropy: Information entropy is an indicator to measure how much information there is in an image. The larger the information entropy is, the




























(a) (b) (c) (d)
Figure 6. Original images and enhanced images..
more details and information can be got from the original image. The information entropy E is defined as
(5)
where is the probability of gray value of i. Assuming the gray scale of a image is from 0 to L − 1, so i = 0, 1, , L − 1.
3) Gray mean: The gray mean reflects the brightness of an image. In a certain range, the larger the image gray mean is, the better the visual effect of the image has. Gray mean can be expressed as
(6)
where g (i, j) represents the pixel value of a image in the i th row and the j th column.
4) Standard deviation: the standard deviation of a image denotes the dispersion degree between the pixel value and the gray mean of the image. A high standard deviation means a high contrast and the better quality of a image. The standard deviation δ can be defined as follow:
(7)
where µ is the gray mean of image.
As can be seen from Tables 1-4, each algorithm can enhance images. HE has an average gray value of nearly 128 when the image is enhanced. This is the result of pixel equalization. The standard deviation of HE is close to 75, which is the largest of all algorithms. Therefore, the enhanced image by HE has the most obvious contrast, which is consistent to the visual effect of the processed image. But the information entropy and average gradient of HE are minimal or close to the minimum, and the information entropy is even smaller than the original image, which indicates that the more details and texture information of images are lost when used the HE algorithm. The average gradient of FDSSR is the largest, which is the result of the enhancement of the fractional differential before SSR, but the information entropy, the gray mean and the standard deviation are small, and the enhanced image is dark and the contrast is small. The proposed algorithm uses fractional integral to denoise the reflection component, so the average gradient is smaller than FDSSR, but it is larger than other algorithms. Also the standard deviation of the proposed method is smaller than HE, and it is larger than other algorithms, which indicates that the image contrast enhancement is obvious. The proposed algorithm has the largest information entropy, which means that the image information is the most abundant, and the detail and texture enhancement effects are the best. The gray mean of the proposed algorithm is the largest except for the image of people. For the image of people, it is obvious that FD has a poor enhancement effect, and a large amount of fog has not been removed, which lead to a higher gray value of the image. SSR, MSR, FDSSR and the proposed algorithm have better defogging effect. The gray mean of the proposed algorithm is the largest of the four methods, which indicates that the enhanced image is brighter and the visual effect is better.
Table 1. Comparison of results of algorithms about the image of building.
Table 2. Comparison of results of algorithms about the image of people.
Table 3. Comparison of results of algorithms about the image of lena.
Table 4. Comparison of results of algorithms about the image of barche.
5. Conclusions
The paper presents an image enhancement method based on fractional calculus and single-scale Retinex. The method uses fractional differential to preprocess the input image. While the image edge information is strengthened, it also can preserve the weak texture and other details of the image non-linearly. Fractional integral is used to denoise the reflection component to reduce and eliminate noise interference. Through experiments, the results show that images enhanced by the proposed method have good visual effects and significantly improve various evaluation indicators.
In future work, adaptive fractional calculus can be introduced into the algorithm to improve the adaptability of the method, but how to determine the correlation factor of the order is difficulty, and improving the versatility of the algorithm also needs further research.
Acknowledgements
This work is supported by the Fundamental Research Funds for the Central Universities (2018MS072).
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Cao, J.G. (2018) An Image Enhancement Method Based on Fractional Calculus and Retinex. Journal of Computer and Communications, 6, 55-65. https://doi.org/10.4236/jcc.2018.611005
References
- 1. Jobson, D.J., Rahman, Z. and Woodell, G.A. (1997) Properties and Performance of a Center/Surround Retinex. IEEE Transactions on Image Processing, 6, 451-462. https://doi.org/10.1109/83.557356
- 2. Rahman, Z., Jobson, D.J. and Woodell, G.A. (1996) Multi-Scale Retinex for Color Image Enhancement. Proceedings of 3rd IEEE International Conference on Image Processing, Lausanne, 19 September 1996, 1003-1006. https://doi.org/10.1109/ICIP.1996.560995
- 3. Jobson, D.J., Rahman, Z. and Woodell, G.A. (1997) A Multiscale Retinex for Bridging the Gap between Color Images and the Human Observation of Scenes. IEEE Transactions on Image Processing, 6, 965-976. https://doi.org/10.1109/83.597272
- 4. Liu, H.B., Yang, J., Wu, Z.P., et al. (2015) A Fast Single Image Dehazing Method Based on Dark Channel Prior and Retinex Theory. Acta Automatica Sinica, 41, 1264-1273.
- 5. Zhang, X., Wang, W.X., Zhang, Y.F., et al. (2015) Vague Aerial Image Enhancement on Fractional Differential and Improved Retinex. Application Research of Computers, 9, 2844-2848.
- 6. Ma, R.G., Wang, W.X., Liu, W., et al. (2016) A Haze Removal Algorithm Combining Fractional Differential, Dark Channel Prior and Retinex. Journal of South China University of Technology (Natural Science Edition), 44, 16-23.
- 7. Zhang, J., Zhou, P.C. and Zhang, Q. (2018) Low-Light Image Enhancement Based on Iterative Multi-Scale Guided Filter Retinex. Journal of Graphics, 39, 1-11.
- 8. He, K.M., Sun, J., and Tang, X.O. (2013) Guided Image Filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35, 1397-1409. https://doi.org/10.1109/TPAMI.2012.213
- 9. Yang, Z.Z., Zhou, J.L., Yan, X.Y., et al. (2008) Image Enhancement Based on Fractional Differentials. Journal of Computer-Aided Design and Computer Graphics, 20, 343-348.
- 10. Yang, Z.Z., Zhou, J.L. and Lang, F.N. (2014) Noise Detection and Image De-Noising Based on fractional Calculus. Journal of Image and Graphics, 19, 1418-1429.
- 11. Land, E.H. (1977) The Retinex Theory of Color Vision. Scientific American, 237, 108-128. https://doi.org/10.1038/scientificamerican1277-108