ABSTRACT

The optimal solution of the multi-constrained QoS multicast routing problem is a tree-like hierarchical structure in the topology graph. This multicast route contains a feasible path from the source node to each of the destinations with respect to a set of QoS constraints while minimizing a cost function. Often, it is a tree. In other cases, the hierarchies can return several times to nodes and links of the topology graph. Similarly to Steiner problem, finding such a structure is an NP-hard problem. The usual tree and topology enumeration algorithms applied for the Steiner problem cannot be used to solve the addressed problem. In this paper, we propose an exact algorithm based on the Branch and Bound principle and improved by the Lookahead technique. We show relevant properties of the optimum hierarchy permitting efficient pruning of the search space. To our knowledge, our paper is the first to propose an exact algorithm for this non-trivial multi-constrained optimal multicast route computation. Simulations illustrate the efficiency of the proposed pruning operations. The analysis of the execution time shows that in simple topologies and with tight QoS constraints the exact algorithm requires relatively little execution time. With loose constraints the computation time cannot be tolerated even for off-line route computation. In these cases, the solution is close to a Steiner tree and heuristics can be applied. These results can serve as basis for the design of efficient, polynomial-time routing algorithms.

Keywords:

Multicast Routing, Quality of Service, Multi-Constrained Steiner Problem, Hierarchy, Partial Minimum Spanning Hierarchy, Branch and Bound

1. Introduction

Quality of Service (QoS) multicasting needs the computation of a multi-constrained multicast route connecting a source node to a set of destinations. The objective of network operators (and transitively of users) is to minimize the network resource consumption. To find an appropriate solution within the feasible solutions, a cost function can be used. The minimum cost solution can minimize for instance the hop count or an additive cost on the links. As it is discussed in [1] , guaranteeing QoS and optimizing resource utilization may be two conflicting interests. We are interested in finding the best cost solution with respect to a set of QoS constraints.

Without QoS constraints, the minimum cost multicast route computation corres- ponds to the well known NP-hard Steiner problem. In our study, we consider the constrained multicast routing with multiple QoS constraints. As it is shown in [2] , the multi-constrained routing problems are NP-hard even if there is only one destination.

Often, in works talking about QoS aware multicast routing, authors suppose that the optimal solution is a partial spanning tree. Section 2.2 gives an overview of the most important related works. In some cases, the optimal multicast route is neither a tree, nor a set of trees, nor a set of optimal QoS paths.

In [3] , it has been mentioned that a feasible/optimal solution of the problem may be different from a tree. Indeed, the authors suggest that it corresponds to a sub-graph containing feasible paths and eventually minimizing a length/cost function. Unfortu- nately, the sub-graph concept is not sufficient to define the optimal solution. Paper [4] shows that a generalization of the tree concept called hierarchy defines accurately the optimum. Furthermore, hierarchies can also describe feasible solutions approaching the optimal one.

To our knowledge, there is no algorithmic solution proposed in the literature to compute the optimal route, which is a hierarchy. In this work, we investigate on finding the optimal solution (the partial minimum spanning hierarchy) of the corresponding multi-constrained partial spanning problem. The problem is NP-hard. Since hierarchies are different from trees and do not obligatory correspond to any sub-graph, the known tree computation algorithms cannot be applied to find the optimal hierarchy. Indeed, hierarchies can contain the same graph node/edge multiple times, and the algorithms based on tree and node enumeration are not suitable for hierarchy computation. Therefore, we propose a particular Branch and Bound algorithm permitting returns to the nodes several times.

Our paper is organized as follows. Section 2 presents the multi-constrained partial spanning problem for multicast QoS routing and provides an overview of the previ- ously proposed approaches to solve the routing problem. Section 3 briefly presents the hierarchy concept generalizing spanning trees as well as the relevant properties of the multi-constrained minimum cost hierarchies. These properties as well as the Look- ahead concept (cf. [2] ) are useful to design the exact algorithm described in Section 4. The computation results can be found in Section 5.

2. The Multi-Constrained QoS Multicast Routing Problem

Often, multimedia applications require multi-constrained multicast routes. For each destination of a given multicast group, the route should meet a set of QoS requirements such as limited delay, jitter, bandwidth, loss rate etc. Indeed, generally the source based QoS multicast routing aims to compute routes by satisfying the given QoS constraints at the destinations and minimizing the network resource consumption or cost.

2.1. Problem Formulation

The network topology is represented by an undirected graph, with the set of nodes V (routers) and the set of edges E (links). The source corresponds to a node 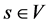and the destination node set is given by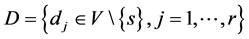. Each edge 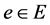is associated with a positive cost 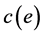and with m QoS weights given by a weight vector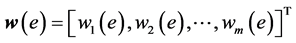. We suppose that the metrics are additive. The weight of a path 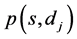is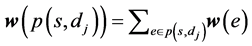. The end-to- end QoS requirements, expressed as constraints from the source to the destinations, are fixed by an m-dimensional constraint vector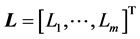. A path 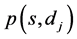is feasible if:

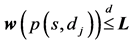(1)

where 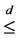is the Pareto dominance.

The multicast QoS routing aims at finding a multicast route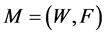, where W is a multi-set of node occurrences (the visited nodes) and F is a multi-set of edge occurrences (the used edge occurrences) in the route¹. If W and F are simple sets, the route is a sub-graph. In our constrained routing problem, M is not always a sub-graph and due to the constraints, the route can visit nodes and edges multiple times [3] [4] . Consequently, a node or an edge may be present multiple times in the multi-sets W and F respectively. We propose to refer to occurrences of nodes and edges/arcs in spite of referring to nodes and edges themselves. This multicast route 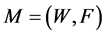must contain at least one feasible path 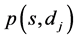from the source node s to each destination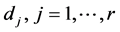. The network resource usage can be expressed by an adequate cost function. The cost may be dependent or independent from the m QoS metrics. Without loss of generality, in the following we suppose an arbitrary additive cost. Therefore, we consider the cost of the multicast communication as the total cost of the forwarded data by using the edges of the multicast structure:

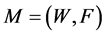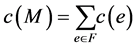(2)

Since the structure M may be different from a sub-graph (the sets W and F are multi-sets with possible repetitions of graph elements), if an edge of G is present twice in F (because it is used twice to forward the multicast messages), its cost must be added twice to.

The following formulation of the optimal QoS multicast routing has been proposed in [4] .

Multi-Constrained Minimum Cost Multicast problem (MCMCM). This problem deals with finding the structure with a minimum cost, containing at least one path from the source node s to each destination that satisfies the given constraint vector:

(3)

As it has been demonstrated, the solution is a directed minimum cost partial span- ning hierarchy [4] . Section 3 recalls the definitions. Finding the optimum is NP-hard.

2.2. Related Works

For solving the QoS multicast routing problem, several propositions aim to compute spanning trees. The reason for basing multicast structures on multicast trees is that the tree structure avoids redundancies (thus minimizes the cost for instance).

Without constraint, the basic problem is known as the Steiner problem. Two large overviews on this well known NP-hard problem are presented in [5] and [6] . The most known exact algorithms are based on the enumeration of the Steiner nodes² and Steiner trees. The solution of the Steiner problem is always a sub-graph (a tree).

If only one constraint (usually on the end-to-end delay) is given, the addressed pro- blem is the Constrained Steiner Tree (CST) problem that is also NP-hard [7] . To solve it, the authors propose a Branch and Bound algorithm by using the Lagrangian Re- laxation and heuristics to get lower and upper bounds in the Branch and Bound tree. A compact Mixed-Integer Program formulation with efficient reduction techniques can be found in [8] . In [9] the diameter-constrained minimum spanning tree variant (DM- STP) is defined. In this problem a natural number D is given, and the goal is to find a spanning tree of the graph with minimum total cost such that the unique path from any node i to any node j has no more than D edges. A Branch and Cut algorithm is pro- posed using heuristics to cutting plane generation. Several heuristics have also been proposed to solve approximately the problem. In [10] , a heuristic that constructs a low cost spanning tree, with respect to a bounded delay on each multicast destination is described. In [11] , an algorithm that approaches the minimum cost spanning tree solution with respect to the delay constraint has been presented. The authors in [12] proposed a heuristic algorithm called The Bounded Shortest Multicast Algorithm (BSMA). The BSMA algorithm always finds a delay constrained tree, if such a tree exists, since it begins with the least-delay spanning tree.

When more than one QoS constraint are considered, the problem becomes more complex, and different tree based solutions are proposed [12] [13] [14] [15] . A rendez- vous point based tree computation has been presented recently in [16] . Three different formulations can be found in [3] . The Multiple Constrained Multicast (MCM) problem aims to compute a sub-graph that contains a feasible path from the source to each destination. Since the sub-graph can be arbitrarily large and the paths are not explicitly identified in this sub-graph, this formulation is not interesting. The Multiple Parameter Steiner Tree (MPST) problem searches for a partial spanning tree minimizing an arbitrary length function. Since the solution of this problem is a tree, it can be configured and used for multicasting. The drawback of this formulation is that in some cases this kind of solution does not exist. The authors say that the MPST, although optimal in terms of resource utilization, does not always satisfy the con- straints. A third formulation is given by the combination of the two cited ones above; the Multiple Constrained Minimum Weight Multicast (MCMWC) problem searching for a sub-graph with minimum cost. Meta-heuristics have also been applied for solving QoS multicast routing. The papers in [17] and [18] propose genetic algorithm based solutions even for networks with uncertain parameters and for energy minimization respectively. The thesis work in [19] presents several metaheuristics (e.g., swarm opti- mization). An original computation of multicast trees based on a Chemical Reaction Optimization Algorithm for QoS Multicast Routing can be found in [20] . Let us notice that these algorithms compute trees and not the optimal solution presented in our pa- per.

In the literature, few proposed algorithms allow solutions that are different from spanning trees. The Multicast Adaptive Multiple Constraints Routing Algorithm (MA- MCRA) [3] is one of the most relevant algorithms that looks for multicast routes that are different from spanning trees. MAMCRA solves the multi-constrained mul- ticast routing problem by computing a special routing structure in two steps:

1) In the first step, the algorithm computes a set of optimal (multi-constrained) paths

2) In the second step, it tries to eliminate the useless redundancies that are produced in the first step.

The result may be a hierarchy (cf. its definition in the next section).

Instead of multiple constraints, different QoS objectives can be established on the QoS values: minimizing the delay, the jitter, the packet losses, etc. A survey on multi- objective minimum spanning tree problem is available in [21] . Our approach is based on multiple constrained formulation.

3. Hierarchies to Solve the Optimal QoS Multicast Routing

Usually, spanning trees are considered as the minimum cost solutions for partial spanning in graphs. However, they have some limitations. Trees can not always satisfy the end-to-end constraints and in some cases there is no tree solution for the problem. As it has been demonstrated in [4] the solution is a connected, graph related structure called hierarchy.

3.1. Hierarchies

Trees are connected (sub-) graphs without cycles. To solve our problem, a structure permitting the graph nodes to be visited several times has been proposed. A hierarchy is a graph-related structure defined as follows [22] .

Definition 1 (Hierarchy) Let be an arbitrary graph and let be a connected graph without cycle (a tree). Let be a homomorphism which associates a node to each node³. The application de- fines a hierarchy in G.

Figure 1 illustrates a hierarchy. In our case, the graph G is the topology graph of the network and the tree represents the routing information (the succession of nodes in the route).

For multicast routing, the route is rooted at the source and we consider rooted hierarchies (the tree T is rooted). A non-empty rooted hierarchy can be considered as a connected route containing occurrences of the graph elements, where each node occurrence has at most one parent node.

Trivially, a hierarchy is not a sub-graph, but (similarly to walks) a graph-related stru- cture. In the example of Figure 1, the nodes c and d are present twice in the hierarchy. Since the different occurrences of the same element can play different roles, the distin- ction and the identification of the occurrences is substantial.

Even though a hierarchy is not a sub-graph, it generates a sub-graph in the graph G. This sub-graph is the image of the hierarchy and may contain cycles. To facilitate the use of the hierarchies, we propose to retain some tree related terms.

A sub-hierarchy of a (rooted) hierarchy H is a hierarchy only containing elements of H.

A branching node occurrence is a node occurrence having at least a degree three in the hierarchy.

A leaf is a node occurrence with a degree one in the hierarchy. In Figure 1, there are three leaves (one occurrence of c, e and f), the second occurrence of d is a branching node occurrence and the reader can easily detect the sub-hierarchy rooted at b.

Hierarchies can be directed or undirected. A directed hierarchy can be related to an undirected graph G. In this case, an arc relies two node occurrences in the hierarchy iff there is an edge between the corresponding nodes in the graph G. If the graph G is not directed, we suppose that each edge can be replaced by a pair of arcs. Moreover, we suppose that the weights of the edge correspond to the weights of the arcs in both directions. The directed rooted partial spanning hierarchy concept allows an accurate and exact definition of the solution of the multi-constrained partial minimum spanning problem. These rooted hierarchies are directed from the source to the destinations. As it has been proved in [4] , the optimal multicast route M, with respect to multiple constraints on positive additive metrics, is always a directed partial spanning hierarchy.

In the following, we refer to this solution as the Multi-Constrained Minimum Partial Directed Spanning Hierarchy, abbreviated by MC-MPDSH. Using the hierarchy con- cept, the MCMCM problem can easily be re-formulated as follows.

The MCMCM problem consists in finding the multi-constrained minimum partial directed spanning hierarchy containing at most one directed path from the source to each destination, with respect to the constraints:.

Figure 2 presents the optimal directed hierarchy solution for two destinations (nodes h and i) when two weights are associated with edges and the QoS requirements correspond to. The cost of all edges is equal to 1 in this example. The cost minimal hierarchy respecting the QoS constraints is drawn with bold arrows. Another feasible tree also exists (drawn with dotted arrows) but this tree is more expensive.

Trees are special hierarchies obtained by injective homomorphism. Thus, a tree is a hierarchy. Some properties of trees are true for hierarchies but not all of them, whereas all properties characterizing hierarchies are true for trees. In [4] , relevant properties of the MC-MPDSH have been enumerated. These properties enable to design efficient exact and heuristic algorithms. Thus, we investigate on the properties of the MC- MPDSH.

3.2. Properties of the MC-MPDSH

We summarize properties that permit the design of our Branch and Bound algorithm by detecting infeasible “solutions” ASAP. The proofs of these properties are generally trivial and omitted in this paper.

1) The leaves in the optimal spanning hierarchy are destinations. Consequen- tly, in an MC-MPDSH there are at most leaves.

2) The directed path from the source s to any arbitrary node occurrence v is a feasible path.

3) The edges of the topology graph G can be used multiple times and in both direction.

4) In a directed path from the source s to an arbitrary destination in the MC- MPDSH, any node has at most one occurrence (a node can not be repeated in a path, paths are elementary). This property is also true regarding the source node itself: no directed path in an MC-MPDSH can return to the source node. Consequently, the source is present only once in an MC-MPDSH.

5) Due to Properties 1 and 4, in an MC-MPDSH, the number of the occurrences of a node is upper bounded by.

6) If a destination corresponds to a leaf node in the optimal solution, then it has only one occurrence (the leaf occurrence).

7) A node can have at most branching node occurrences.

8) Let be a sub-hierarchy of an MC-MPDSH with leaves. Let be the occurrence of the node in the sub-hierarchy and its out-degree. For the occurrences of the node v, the following inequality always holds:

(4)

Remember that the metrics in the graph are positive and additive. The following property enables to establish an important relation between the QoS constraints and gives a sub-optimality property.

9) Let be an MC-MPDSH rooted at s. It satisfies the constraints in the lea- ves. Let be a sub-hierarchy of rooted at. Let be the wei- ght vector of the path in. The sub-hierarchy is an MC-MPDSH from v to the destination occurrences that it contains, with respect to the constraints ⁴.

10) Several paths from the source to different destinations can use an edge. We say that two paths share an edge in a hierarchy if the same occurrence of the edge belongs to both paths.

Let and be two paths from the source to two distinct destinations both con- taining an edge a. The edge a is shared by and in the MC-MPDSH, iff the pre- fix of and from the source to the edge a is the same:.

Figure 3 illustrates a graph, that contains only one feasible path and another from the source s to the destinations and respectively. In the minimum cost spanning hierarchy, the two paths can share the edge (the prefixes are the same, i.e. this prefix is empty), but they cannot share the edge. (The edge is present twice in the hierarchy, as it is illustrated by the associated T in the figure).

This study of the properties of the optimal solution is very useful to design exact al- gorithms and heuristics. Our proposal for an exact Branch and Bound algorithm fo- llows.

4. MC-MPDSH Computation by Branch and Bound Algorithm

The multi-constrained multicast routing problem is NP-hard. Unfortunately, the algo- rithms proposed to solve the Constrained Steiner Problem such as the Steiner Tree Enumeration Algorithms and the Topology Enumeration Algorithms cannot be applied here, because of the allowed multiple occurrences of the graph elements in the solution. In the following, we present a Branch and Bound algorithm that exactly solves the MCMCM problem. The efficiency of this kind of algorithms depends strongly on the applied pruning operations. In our algorithm, two ways are proposed to reduce the search space and accelerate the computation:

・ pruning based on properties of the possible optimum as presented in the previous section.

・ pruning based on the Lookahead concept.

We will demonstrate that the proposed pruning operations accelerate significantly the computation.

4.1. Main Algorithm

Despite the fact that there are repeated nodes and edges in a hierarchy, the Branch and Bound algorithm can easily be adapted for the spanning hierarchy computation. The proposed framework (cf. Algorithm 1) is a frontier search type Branch and Bound algorithm. It allows the enumeration of the partial spanning hierarchies, which are candidates to lead to the solution. Each node in the virtual search tree corresponds to a hierarchy rooted at the source node. Generally, these hierarchies are sub-hierarchies, potential feasible germs of the solution spanning the destinations. The frontier is the set of leaves in the search tree. It is initialized with a hierarchy that contains only the source node s. At each step of the algorithm a simple greedy strategy is applied: the hierarchy H with the best cost is selected from the frontier. The first hierarchy in the course of the enumeration, which covers all destinations and satisfies the end-to-end constraints corresponds to the optimal solution and is returned. If the destinations are not yet covered by the selected hierarchy, possible continuations of this selected hierarchy H are computed to create larger hierarchies. These successors are then added to the frontier. The particularity of the problem is that repeated elements may occur in the continuations. If there is no hierarchy in the frontier satisfying the end-to-end constraints, the problem has no solution. The first steps of the search tree exploration is illustrated in Figure 4.

Let K be the frontier (the set of leaves in the search tree). The meta-code of the main algorithm for computing the MC-MPDSH is given by Algorithm 1.

The brute enumeration of all possible hierarchies is very expensive. However, the properties of the optimal solution and the Lookahead technique permit to realize pruning operations. We analyze the efficiency of these accelerations in the following section. The crucial question is how the valid successors of a selected hierarchy H are computed to continue the enumeration of hierarchies in the search tree. Duplication of spanning hierarchies should be avoided and all possible candidates should be enume- rated.

4.2. Computation of the Successors

To enumerate the candidate hierarchies, we propose the following construction. Like trees, hierarchies can always be decomposed into layers. In our case, we consider that the source corresponds to layer 0. When new edges are added to a selected hierarchy in

Algorithm 1. Branch and Bound algorithm to compute the MC-MPDSH.

Requier: the weighted graph, the weight vector and the cost for each edge, the source node s, the destination set D and the constraint vector

Ensure: H the MC-MPDSH if it exists

{the start point containing only the source}

{ is the set of the leaves in the search tree}

whiledo

select from with minimal cost

if then

return {it is the optimal solution}

successor_hierarchies_of() {cf. Algorithm 2}

for all do

{add to }

end for

{delete from }

end while

STOP without solution

the algorithm, these edges are added always at the highest layer of the hierarchy. This layer contains only leaves. If the selected minimum cost hierarchy have n layers, the new successor hierarchies will have layers. Following the example in Figure 4, the successors of the root hierarchy (containing only the source) are hierarchies having two layers (and never three). The successors of the hierarchy selected in the example are hierarchies having three layers and the new edges are added only to the leaves of layer 1.

Let H be the selected hierarchy and let be the set of the leaves in the last layer of H. The successors of H in the search tree are the hierarchies enlarged by adjacent edges from. We call this kind of edges fringe edges, expression borrowed from [24] . Since a node can not be repeated in any path (Property 4), edges returning to the parent node of a leaf are not in the fringe edges. The fringe edges of a hierarchy are illustrated by Figure 5.

The computation of the set of successors of a given hierarchy H is described by Algorithm 2. Only the hierarchies, which correspond to the end-to-end constraints and to the properties of the optimal solution and which are not excluded by the Look- ahead (cf. Subsection 4.3) can be sub-hierarchies of any solution. To simplify, we call them valid candidate hierarchies. The algorithm proceeds in two steps.

In the first step, it selects the set of fringe edges (indicated by A) of the hierarchy H. (Non empty combinations of these edges can be added to H to create successors in the second step.) Trivially, if a fringe edge f leads to a new leaf that violates the QoS con- straints, f is not added to the set A (the QoS constraints must be respected in the new leaves of the successor hierarchies, cf. Properties 2 and 9). Moreover, a node can not be repeated twice in a path from the source in the optimal solution (Property 4). Con- sequently, a fringe edge from a given leaf a is not added to the candidate set A if its other extremity already belongs to the set of parents of a.

Algorithm 2. Computation of successor hierarchies.

Require: the weighted graph, the hierarchy H corresponding to the current node in the search tree

Ensure: the set of successor hierarchies of H with respect to the end-to-end QoS requirement and Properties

set of possible adjacent edges

Step 1: Selection of all possible fringe edges for

for all leaf of do

adjacent_edges_of {adjacent edges of }

parents_of {set of parent nodes of in }

for all edge do

{computation of possible adjacent edges of }

opposite_node_of

{accumulated weight at }

if then

end if

end for

end for

Step 2: Combination of the fringe edges computed in Step 1

for all combination of the edges in do

{add the edges of to }

{set of reachable destinations}

if (number_of_leaves and max-degree_of_nodes and) then

{add as new successor to S}

end if

end for

In the second step, the algorithm combines the selected fringe edges (enumerated in the first step) for construction of valid successors. Since the optimal hierarchy can have at most leaves, only successors corresponding to this limitation are enumerated (Property 1). Following Property 7, the branching node occurrences of a given node

cannot exceed. Property 8 permits to verify the sum of the degrees of the

occurrences of the nodes present in a new configuration. Moreover, if a new com- bination does not permit to reach all the destinations (see also in the next sub section), the combination is deleted and not added to the successor set.

In the worst case, the algorithm constructs at most valid candi- date hierarchies, where k is the number of fringe edges that are added to A in step one.

Many other not valid hierarchies (which do not match any solution) can be detected using the Lookahead technique. In the following we summarize the adaptation of the Lookahead technique in our case.

4.3. Application of the Lookahead

The Lookahead is originally used in Artificial Intelligence [25] [26] to accelerate the computation by applying upper bounds and reducing the search space. The concept was successfully applied in the computation of optimal paths under multiple constraints [2] . In our case, in a node reached on a path from the source, one can con- sider the remaining information of any path toward the destinations and decide if this node can be usefull and considered for the computation or not. More precisely, the Lo- okahead concept can be applied in the computation of the optimal hierarchy as follows.

At first, we compute the m shortest path trees from each destination to all other nodes by considering the m metrics. shortest path trees (computed in poly- nomial time) are obtained. To store the different computed values at each node, two propositions can be considered:

1) All values from this node to the destinations are saved in Lookahead vectors (initially values at each node). In the following, we denote by the Lookahead vector computed for the node v regarding the destination. In this construct, trivially, where is the shortest path from v to regarding the metric i. When a destination is reached, the vectors are updated (one can remove the corresponding Lookahead vectors).

2) Only one m-dimensional vector is considered in each node v with the smallest values from this node to the closest destination concerning each metric. For this vector,. This vector is constant and cannot be reconsi- dered.

Trivially, the first method consumes more memory but it is more precise and effi- cient for pruning. In this study, we implemented the simpler second solution: only one Lookahead vector per node was used.

It is important to state that the computation of the Lookahead vectors is held off-line, before the construction of the candidate hierarchies. Then these vectors can be used at the computation of valid successors. For each fringe link selection (first step of Algo- rithm 2), the following additional test can be performed.

・ Let f be a fringe edge from node a in the hierarchy to a newly examined node b. Trivially, if, there is no further destination which can be reached from b respecting the constraints. The fringe arc can not be used to create successors (there is no feasible path to any destination).

In Step 2, the algorithm combines these edges and generates new candidates. The usefulness of each combination can be tested by using the Lookahead information, if the Lookahead vector is available for each destination.

・ Let be the set of leaves of the candidate hierarchy. (B contains the extremities of the newly added fringe edges and also leaves, which are not concerned by the new fringe edges.) Let be the set of “reachable” destinations from. For a “reachable” destination, ⁵. For each com- bination, the set of destination which can be achieved by the combination can be computed. If the set does not cover all the destinations, this new hierarchy combination is not added to the candidate set.

Figure 6 illustrates the fist Lookahead test. The source is the node s and two destinations are concerned (nodes k and m). Two metrics are used and the link values are indicated. The computed Lookahead vectors are also indicated with bold characters near the nodes. During the first iteration, there are three candidates to create eventual successors of the source, and. However, if we consider the remaining information stored at node g, two candidates can be removed and only the second one can be considered for the continuation.

4.4. Exactness of the Proposed Branch and Bound Algorithm

It is important to state that Algorithm 2 computes all valid hierarchies without skipping any of these hierarchies, even if it considers the proposed pruning operations.

Lemma 1. Algorithm 2 does not create duplication.

Proof. Remember, the successors are created following the layers of the hierarchies. Starting from a hierarchy selected by Algorithm 1, non-empty combinations of fringe edges are added to create successors. A given combination is added only once to. Two identical successors can not be produced from the hierarchy.

Let us suppose that there are two identical hierarchies and produced from two different hierarchies and. The last layer of (and also in) contains the fringe edges. By deleting these fringe edges, the previous hierarchies can be obtained. These previous hierarchies are the same by deleting the same fringe edges both from and from. The contradiction is trivial.

Lemma 2. Algorithm 2 enumerates all valid candidate hierarchies without skipping any of them.

Proof. Let us suppose that there is a hierarchy with less cost than the optimum and this hierarchy is skipped. By deleting the fringe edges from, the hierarchy is obtained, which is also valid and of less cost. Since is not enumerated, can not be enumerated because there is no filter from to. In this way, recursively we can arrive in the route hierarchy, which can not be enumerated by the algorithm. It is absurd.

Theorem 1. The proposed Branch and Bound algorithm returns the MC-MPDSH if it exists.

Proof. The algorithm enumerates all the valid candidate hierarchies before arriving at the solution (Lemma 2). The valid candidates are selected by Algorithm 1 in an increasing order of costs. If a hierarchy H is selected, then there is no solution with less cost than the cost of H (otherwise is selected to examine). The first selected hierarchy spanning all the destinations is the MC-MPDSH.

5. Performance Evaluation of the Branch and Bound Algorithm

To analyze its performance, the algorithm have been executed in two benchmark networks. The first is the DARPA CORONET CONUS topology with 75 nodes and 99 links (illustrated by the first topology in Figure 7). The second is the NTT (Nippon Telephone Telegraph of Japan) network topology. This network contains 55 nodes and 144 links (the second topology in the figure).

In the presented simulations, three or four metrics were associated with each link and the link values were randomly generated from the same integer set (for example from) for each metric. We also considered the cost as a random value (corresponding to the first metric).

Different constraint vectors are generated from tight to loose ones. For a given destination d, we can consider the tightness of constraints as follows. For each metric i, a shortest path with length can be computed. This length is a lower bound for the feasible solutions from the source to this destination regarding this metric. A vector of constraints can be considered as tight, when the constraints are close to the upper bounds but there is at least a feasible solution. Contrarily, when the constraints are far from the upper bounds, feasible solutions are easier to find, we consider the con- straint vector as loose.

The execution time of the algorithm is quasi proportional to the number of computed hierarchies in the search tree. In this study, we use this number as a funda- mental performance metric. A second metric can be the number of iterations before ob- taining the solution.

5.1. Relevance of the Pruning and Lookahead

Due to the possible repetitions of nodes and edges in the spanning hierarchies, their enumeration by the Branch and Bound exact algorithm is more expensive than the enumeration of the more restricted spanning trees. However, the presented properties of the optimal hierarchy allow to implement efficient pruning. In addition to the pruning operations, we expect that the application of the Lookahead concept will also reduce considerably the search space.

To measure the impact of both the pruning operations and the Lookahead technique, three variants of the algorithm have been executed: 1) BBB: the basic Branch and Bound algorithm without pruning and Lookahead 2) BBwP: the algorithm improved by pruning based on the properties of the solution 3) BBwPLA: the algorithm with both the pruning and Lookahead operations.

At first, we executed the three algorithms in CORONET network for a multicast group of five arbitrarily chosen members. With randomly generated link values and moderately tight constraints⁶ ten executions were launched, and only the first 20000 iterations of the algorithms were registered. Significant differences between the performances were observed. Figure 8 illustrates the progression of the algorithms sh- owing the average number of computed hierarchies in the ten executions and the corresponding table indicates the average number of the computed hierarchies at the end of the 20,000 iterations.

The results show the efficiency of the propositions. In the example, the proposed pruning operations and the Lookahead technique divide the number of enumerated hierarchies in the search tree by more than ten.

5.2. The Impact of the Tightness

The value of the constraint vector influences strongly the computation time. The tight- ness of the constraints is relative to metrics and destinations. With a given constraint vector and for some destinations, one can find several QoS routes satisfying the constraints whereas it is not possible for some other destinations. Since the solution (the spanning hierarchy) should cover all the destinations, we consider that the tightness always concerns the most critical destination.

Intuitively, when the constraints are loose (for all destinations), the optimal solution is a route of minimum cost but practically without constraint. It converges to the mini- mum Steiner tree. We will see that our Branch and Bound algorithm (which permits largely node repetitions) is not efficient to compute usual spanning trees (which are without node repetitions).

The enumeration of the possible hierarchies with potential node repetitions becomes essential, when the constraints are tight. In these cases both the Lookahead mechanism and the pruning operations are more efficient. The following experiences illustrate this effect. Let us notice that the computation of the exact solution is expensive. We developed only a few examples but the results are qualitatively similar in these examples.

In the DARPA CORONET CONUS topology, we tested the algorithm (the proposed BBPwLA version) for an arbitrarily configured multicast session with different con- straint vectors. The (randomly selected) source was in Austin and five destinations were (also randomly) selected at nodes Abilene, Buffalo, Los Angeles, Billings and El Paso. In this computation, three metrics were associated with each link and the values were generated randomly from the integer set. The cost corresponded to the first metric.

We computed the optimal solution for several QoS requirements. Since the link values were generated from the same range, we used the same end-to-end constraint for the three metrics. Table 1 resumes the results on the number of iterations and com-

puted hierarchies to obtain the optimal solution. In the observed case, there is no solution with the constraints. In this way, we can consider that the vector corresponds to a tight constraint vector and the higher values are looser. For instance, the solution with minimum cost for the constraint vector (with cost 38) was obtained after 72,615 iterations and computing 267,228 hierarchies. The solution with the same quality (with cost 38) was also obtained with the tighter constraints after 6452 steps in the Branch and Bound algorithm compu- ting only 14,334 hierarchies.

The progression of the computation is illustrated by Figure 9. This experience shows that the computation becomes longer with loose constraints (curves are stopped quickly in tight environment).

Why not compute the optimal solution with tighter constraints, if the computation is faster? Unfortunately, the response is negative. Tight constraints do not always implicate the same quality and cost that can be obtained with loose constraints. Intui- tively, loose constraints permit to compute a solution near the cost minimal Steiner tree but at the expense of the QoS. With tighter constraints (satisfying tighter quality requi- rement) the optimal solution can have higher cost. This phenomenon is illustrated by the following example. In the CORONET CONUS topology for the same multicast group but using differently generated random link values, the following results were obtained. In this case, there is no solution for the constraint vector and the vector can be considered as tight constraint vector. We computed the exact solution with four constraint vectors as it is shown in Table 2. Figure 10 shows the progression of the algorithm in the different cases. For tight constraints, the optimal solution is obtained rapidly (computing 14,334 hierarchies) but he cost is higher (49) than the cost (37) obtained in the case of loose constraints. The solutions are different. To obtain the optimal solution for the constraint vector, the computation of 128,927 hierarchies was needed.

A third computation case study was performed in the NTT network topology. The link values were generated randomly between 1 and 5 and for four QoS metrics. A mul- ticast group of four destinations (nodes 8, 17, 25 and 28) and a source (node 14) were also randomly selected. For the constraint vector there is no solution in the generated case, and the tight constraints permitting a feasible solution correspond to. With different feasible constraint vectors, the following solutions were obtained (cf. Table 3).

With looser constraints the cost diminishes as it is expected. The particularity of this case is that with the constraints the number of iterations (the number of the selected hierarchies from the front of the search tree) is less (17,527) than with the constraints (24,039), but the number of computed successor hierarchies is higher. The loose constraints implicate less pruning operation and in this way, the number of computed successors increases rapidly. But, as it illustrated in this example, the computation can be terminated using less iterations. The progression is shown by Figure 11. Our summary concerning the results is as follows.

The investigated simulations corroborate our intuitions. In the case of loose constraints, the exact algorithm is very expensive, even if the pruning operations limit the search space. In this case, the solution is close to the Steiner tree. The enumeration of the candidate hierarchies can not be tolerated in real route computations. Steiner heuristics can offer solutions. Contrarily, in the case of tight constraints, due to the pruning, the number of computed candidate hierarchies is lower and the proposed al- gorithm or a somewhat modified variant of this algorithm can be used.

6. Conclusions and Perspectives

The exact solution of the multi-constrained QoS multicast routing problem corres- ponds to a directed rooted hierarchy. However, finding feasible and/or minimum cost

hierarchies are NP-hard problems. Exact algorithms to compute the optimum have not yet been proposed. The algorithms computing heuristic solutions manipulate trees and sets of paths rooted at the source. We argue that it is essential to identify the optimal solution of the addressed problem. It is clear that this solution does not obviously belong neither to the set of minimum cost paths nor to the set of shortest paths computed by using the earlier proposed and known non-linear length. Since hierarchies may contain multiple occurrences of a node or an edge/arc, most of the enumeration algorithms are not appropriate to compute the optimal solution. The main result of our investigations in this paper is an exact Branch and Bound algorithm to compute the optimal hierarchy. We proved that the proposed algorithm finds the optimum if it exists. To accelerate it, the design of the algorithm is based on some important pro- perties of the hierarchy-type solutions. Moreover, the Lookahead concept is applied successfully. The simulation’s results highlight the gain on the computation time, when the algorithm considers the proposed pruning operations. Due to the complexity of the problem, the exact algorithm cannot be applied for routing in large networks. Your results illustrate that in the case of loose QoS constraints, the solution can be a tree and in this manner modified Steiner heuristics can be applied. In the case of tight con- straints, the number of computed candidate hierarchies is limited and we can hop the design of efficient quasi-exact algorithms. These first results on the optimum are good start points for the future design of routing algorithms.

Acknowledgements

I thank Dr. Samer Lahoud, associate professor at the University of Rennes 1, who has worked with me on an earlier version of the proposition. I thank also Dr. Fernando Kuipers, associate professor at Delft University of Technology, who proposed the app- lication of the Lookahead concept. Finally, the algorithm has been implemented by Dimitri Morere, master student at the University of Montpellier.

Cite this paper

Molnar, M. (2016) Exact Algorithm to Solve the Minimum Cost Multi-Constrained Multicast Routing Problem. Journal of Computer and Communications, 4, 57-79. http://dx.doi.org/10.4236/jcc.2016.414005

References

NOTES

¹To facilitate the analysis, we use undirected graph models despite the fact the route is directed. We consider the links can be used in both directions and the weights and cost values are the same in both directions.

²A Steiner node is a node that has a degree greater than two in the spanning tree.

³A homomorphism preserves the adjacencies of nodes; and can be adjacent if the corresponding nodes and are also adjacent.

⁴This property corresponds to the well known Bellman’s principle of optimality [23] and permits to search the optimal solution with dynamic programming. Unfortunately, the computation of all the smallest and possible sub-hierarchies is expensive. Remember that the problem is NP-hard.

⁵It is not sure that a “reachable” destination can be reached using the proposed test. What is sure is that it cannot be reached if the condition is not satisfied.

⁶The selected constraints were neither tight nor loose.