Journal of Computer and Communications
Vol.02 No.14(2014), Article ID:52339,6 pages
10.4236/jcc.2014.214005
Research on Location-Inventory Model in Grain Emergency Network
Lin Wang, Wenzhuo Liang, Yunxian Hou
College of Economics and Management, China Agriculture University, Beijing, China
Email: wanglincau2013@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 October 2014; revised 6 November 2014; accepted 26 November 2014
ABSTRACT
Once the disaster occurred, a huge amount of grain supply is needed from disaster area. Because of the short shelf life, grain is very strict with reserve environment and needed to rotate on a regular basis in the process of reserves. Considering the limitations of existing related research, this paper presented a facility location model for grain emergency network that incorporates inventory factors and rotation mechanism, and then designed genetic algorithm based on Matlab to solve the model. Finally we verified the feasibility and effectiveness of the algorithm by computational examples and presented the directions for future work.
Keywords:
Location-Inventory, Grain Emergency Network, Genetic Algorithm

1. Introduction
Disasters often cause significant loss of life and property, which can be both natural (earthquakes, hurricanes) and man-made (terrorist attacks, chemical leakages). Statistics show that more than 500 disasters are estimated to strike our planet every year, around 75,000 people are killed and more than 200 million others are impacted [1] [2] . Especially in the 21st century, disasters occur more frequently, so most countries have established several series of emergency plan to deal with such disasters. However, only relying on emergency plans, the emergency relief supplies (especially grain) cannot be delivered to the stricken area in time, because the disasters generally occurs rapidly and they are difficult to predict, the rapid response times and huge demand is required, and even more emergency facilities may be damaged.
The Chinese Government has established a set of central and local grain reserve system, in response to unexpected public emergency events. However, the current China’s grain reserves are mostly unprocessed, so it needs time and conditions to transform the raw grain into processed grain. The 2008 Wenchuan earthquake provides an excellent example that directly revealed the shortage of processed grain reserves. Therefore, China has been making the planning and construction of processed grain reserve system. Many national policies such as “National Food Security and Long-Term Planning Framework (2008-2020)” and “Food Industry Development Plan during the 12th Five-Year Period”, indicate that the number of provincial designated emergency food processing enterprise increases from 1700 to 2000, the number of food supply industry increases from 4000 to 5000, and the processed grain emergency reserves (EPI) of city should meet the consumption needs of more than 15 days.
At present, although the theorists pay more attention to emergency rescue, concerning to the study about the emergency supply of grain is very insufficient. Through analyzing the operation of emergency supply of grain, it is not difficult to find that the emergency supply system of grain can be viewed as a three-stage supply chain formed by the raw grain suppliers, core enterprise and supply outlets. Due to the short shelf life of processed grain, high storage conditions, requirement of quick rotation, there will lead to a substantial increase in the cost of processed grain reserves, if reserved by local government. Therefore some enterprises which have some production and reserve capacity are assigned and commissioned to stock up on processed grain and also receive subsidies from local government. In the absence of disaster, core enterprise may carry out normal production, marketing and other routine operations on the premise of a certain quality and quantity of processed grain reserves. Once disaster occurs, core enterprise need to distribute the processed grain reserved in advance to the supply outlets of stricken area for the first time, to gives priority to the demands from stricken area.
The current researches on emergency network optimization are mainly concentrated in emergency facility location. The traditional facility location problem can be divided into: p-median problem, p-center problem and covering problem [3] -[7] . And covering problem is the most widely used model in facility location problem, especially in the location of emergency facilities. With the further research, scholars have gradually realized that the basic hypothesis of traditional covering problem is not reasonable in many cases. When the distance between the disaster area and facilities is less than certain distance (time), that was thought to be completely covered; otherwise, the disaster area will not be covered, this assumption is called 0 - 1 covering problem. Therefore scholars put forward a series of improvement ideas, such as the maximal covering location with coverage gradually [8] , the set covering model with multi-coverage [9] [10] , multiple quantity and quality of coverage model [11] , multistage covering location model [12] -[14] , the maximal covering location with backup facilities [15] , and other facility location models with different constraints [16] -[24] .
Through the summary of many facility location models, we found that the current related research only limits the conventional emergency facilities or general emergency materials reserve site selection problem, and ignores the study of the emergency supplies of grain, a special emergency material, which has obviously different characteristics from the general emergency materials in the process of emergency stockpile. Once the disaster occurred, a huge amount of grain supply is needed from disaster area. Because of the short shelf life, grain is very strict with reserve environment and needed to rotate on a regular basis in the process of reserves. So, it is of great importance to research on grain emergency network, especially to determine the scope of reserve enterprise, location, service scope and inventory strategy.
2. Method
2.1. Problem Description
We consider a three-tiered system consisting of one or more suppliers, reserve enterprises and supply outlets. We assume that the locations of the reserve enterprises and supply outlets are known and that the reserve enterprises have infinite capacity at least from the perspective of the system being modeled. The problem is to determine the optimal number of reserve enterprises, their locations, the supply outlets assigned to each reserve enterprise, and the optimal ordering policy at the reserve enterprises.
We do not explicitly model the inventory maintained by the supply outlets themselves. A key problem is that the demand that is seen by each reserve enterprise is a function of the demands at the supply outlets assigned to the reserve enterprise. Thus, the inventory policy―the reorder interval, reorder size, and safety stock―at the reserve enterprise is a function of the assignment of supply outlets to the reserve enterprise. Since these assignments are not known a priori, the inventory policy must also be endogenously determined. Moreover, we assume that the storage capacity of reserve enterprise is unlimited, and the cost of transportation from reserve enterprise to supply outlets only depends on the fixed cost of transportation and the distance.
2.2. Model Formulation
2.2.1. The Safety Stock Cost
We let 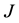 be the set of reserve enterprises indexed by
be the set of reserve enterprises indexed by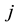 , and
, and 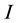 be the set of supply outlets indexed by
be the set of supply outlets indexed by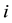 . Assume that the demand at each supply outlet is normally distributed with a daily mean
. Assume that the demand at each supply outlet is normally distributed with a daily mean 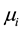 and a daily variance
and a daily variance 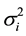 and let
and let 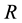 be the set of supply outlets assigned to the reserve enterprise. Let
be the set of supply outlets assigned to the reserve enterprise. Let 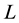 be the lead time in days for deliveries from the supplier to the reserve enterprise. So the lead time demand at the distribution center is
be the lead time in days for deliveries from the supplier to the reserve enterprise. So the lead time demand at the distribution center is
normally distributed with a mean of 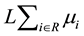 and a variance of
and a variance of . The safety stock required to ensure that stockouts occur with a probability of
. The safety stock required to ensure that stockouts occur with a probability of 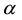 or less is
or less is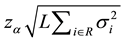 , where
, where  is a standard Normal deviate such that
is a standard Normal deviate such that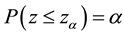 .
.
2.2.2. The Annual Working Inventory Cost
Let 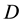 be the expected annual demand, so
be the expected annual demand, so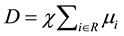 , where
, where 



where 





Taking the derivative of expression (1) with respect to
rivative to zero, we obtain
nual working inventory cost of

2.2.3. The Emergency Reserve Cost
Because of the short shelf life, grain is very strict with reserve environment and needed to rotate on a regular basis in the process of reserves. During the period of emergency reserve, the rotation cost plus the storage cost make the emergency reserve cost. Let 




2.2.4. Location-Inventory Model Formulation
Let 




With this notation, we can formulate the problem as follows:

Subject to:




The first term of the objective function (4) is the fixed cost of locating facilities. The second term represents the local delivery cost. The third term represents the total working inventory cost. The fourth term represents the safety stock cost. The fifth term represents the emergency reserve cost. Constraint (5) states that each demand node must be assigned to a reserve enterprise. Constraint (6) stipulates that the assignments can only be made to open reserve enterprises. Finally, constraints (7) and (8) are standard integrality constraints, with (8) represent- ing single-sourcing constraints, meaning that all of the demand at a supply outlet must be assigned to the same reserve enterprise.
3. Model Algorithm Design
For the number of reserve enterprise is uncertain, the established location-inventory model of grain emergency network is a NP-Hard problem. Classic algorithms for solving location-inventory problems is the Lagrangian relaxation algorithm [25] , but with more complicated constraints and planning scope expands, the algorithm need a longer computation time. So in this paper, we use the genetic algorithm to solve the location-inventory model.
1) Coding work
Choose 

2) Initialization
Set evolution algebra counter



3) Calculation the fitness of each individual
Step 1: Assign each supply outlet to its nearest reserve enterprise, until all retailers are assigned;
Step 2: Test on each supply outlet in turn. Delete the supply outlet from the enterprise which it was originally assigned to, and then assign this supply outlet to the other reserve enterprise. If the new scheme can reduce the total cost, update this scheme; if not, assign this supply outlet to another reserve enterprise until the total cost cannot be reduced by assigning this supply outlet to any reserve enterprise.
Step 3: If all the supply outlets get through the examination of step 2 and the original scheme has not changed, then in step 4; if not, return to step 2 to examine each supply outlet in turn.
Step 4: According to the above steps to get the optimal scheme 

4) Choose operation, crossover operation and variation operation
The roulette wheel selection method is adopted for the choice of individuals. First calculate the fitness of each
individual
heredity to the next generation of most likely. Using discrete restructuring to make crossover operation can produce new individual more effectively from two similar structures in the parent. Generation replacement method is used for population iteration, to keep only one when appear some same individual and avoid the GA convergence too fast, can also prevent the solution into a local optimal solution at the same time.
5) Conditions for the termination judgment
If
4. Computational Results
In this section, we present computational results from an experiment. We assume that there are 10 candidate reserve enterprises and 50 supply outlets, and their positions are random uniform distribution on the [0, 100] of the plane. In addition 







Table 1 shows the parameters for computational operation that we assumed.
The computational results are shown in Table 2 and Figure 1.
Table 1. Parameters for computational operation.
Table 2. Computational results for location-inventory model.
Figure 1. Computational results of reserve enterprises and supply outlets.
Table 2 shows that there are 10 candidate reserve enterprises and 50 supply outlets in the computational experiment. The optimal objective function value is 475,000 and 5 candidate reserve enterprises have been selected finally. The calculation process has elapsed for 16.5 seconds after 76 evolutions. Shorter elapsed time and less number of iterations show the effectiveness of the algorithm.
In Figure 1, there are three kinds of symbol depict the reserve enterprises and supply outlets. Among them, “o” was on behalf of the supply outlets, “+” was on behalf of the selected reserve enterprises and “△” was on behalf of the unselected reserve enterprises. We can find that 5 candidate reserve enterprises have been selected finally, in order to minimize the total cost.
In this computational examination, we have designed genetic algorithm to solve the model, which does not mean that only genetic algorithm is appropriate. We choose genetic algorithm is just because of its advantage, which has good global search ability and can quickly search out all the solution in the solution space, and won’t get into local optimal solution of the rapid decline in trap.
5. Conclusions and Directions for Future Work
We have presented a facility location model for grain emergency network that incorporates inventory factors and rotation mechanism, and then designed genetic algorithm based on Matlab to solve the model. Finally we verified the feasibility and effectiveness of the algorithm by computational examples.
We assume that the storage and service capacity of reserve enterprise are unlimited in this paper, but in reality, they are key points which should be considered and cannot be ignored. The storage limit of reserve enterprise will affect the final number and location assigned to the supply outlets, as well as their own inventory control strategy. And also, the construction cost will increase with the ascension of the capacity, which is no longer a fixed value but a function about the capacity. So the grain emergency network optimization with capacity limits will be a further development direction.
Acknowledgements
This article could not have been completed without the help and support of many people. We express our deepest gratitude to the reviewers and editors, whose able guidance helped in the publication of this article. This work is supported by National Social Science Fund (Grant No. 14BGL062), the National Science & Technology Pillar Program during the 12th Five-Year Plan Period (Grant No. 2014BAL07B04, 2014BAL07B05) and the Beijing Modern Logistics Research Base Open Project (Grant No. JD2013003).
References
- Wassenhove, L.N.V. (2006) Humanitarian Aid Logistics: Supply Chain Management in High Gear. The Journal of the Operational Research Society, 57, 475-489. http://dx.doi.org/10.1057/palgrave.jors.2602125
- Caunhye, A.M., Nie, X.-F. and Pokharel, S. (2012) Optimization Models in Emergency Logistics: A Literature Review. Socio-Economic Planning Sciences, 46, 4-13.
- Schilling, D.A., Jayaraman, V. and Barkhi, R. (1993) A Review of Covering Problem in Facility Location. Location Science, 1, 25-55.
- Farahani, R.Z. (2012) Covering Problems in Facility Location: A Review. Computers and Industrial Engineering, 62, 368-407. http://dx.doi.org/10.1016/j.cie.2011.08.020
- Church, R. and ReVelle, C. (1974) Maximal Covering Location Problem. Papers of the Regional Science Association, 32, 101-118.
- Toregas, C., Swaim, R., ReVelle, C. and Bergman, L. (1971) The Location of Emergency Service Facilities. Operation Research, 19, 1363-1373.
- Roth, R. (1969) Computer Solutions to Minimum Cover Problems. Operation Research, 455-465.
- Berman, O., Dreznerb, Z. and Krass, D. (2010) Generalized Coverage: New Developments in Covering Location Models. Computers and Operations Research, 37, 1675-1687. http://dx.doi.org/10.1016/j.cor.2009.11.003
- Daskin, M.S. and Stern, E.H. (1981) A Hierarchical Objective Set Covering Model for Emergency Medical Service Vehicle Deployment. Transportation Science, 15, 137-152. http://dx.doi.org/10.1287/trsc.15.2.137
- Liu, T.-H., Xu, W.-S. and Wu, Q.-D. (2010) Modeling and Algorithm Forlocation of Medical Resources Underlarge- Scale Emergency. Computer Engineering and Applications, 46, 13-17.
- Ge, C.-J., Wang, X. and Guan, X.-J. (2011) A Multi-Covering Model and Its Algorithm for Facility Location Response for Large-Scale Emergencies. Operations Research and Management Science, 20, 50-56.
- Wang, W.-F., Guo, B. and Liu, X.-L. (2007) Model and Solution Approach for Multiple-Quality-of-Coverage Facility Location Problem. Chinese Journal of Management Science, 15, 144-148.
- Xiao, J.-H. and Hou, Y.-X. (2012) A Multistage Covering Location Model for Emergency Supplies Reserve. Statistics and Decision, 23, 45-48.
- Xiao, J.-H. and Hou, Y.-X. (2012) Bi-Objective Emergency Facility Location Model and Algorithm Considering Multi-Level Gradual Coverage. Soft Science, 26, 127-131.
- Hogan, K. and Re Velle, C. (1986) Concepts and Applications of Backup Coverage. Management Science, 32, 1434- 1444.
- Ma, Y.-F., Yang, C. and Zhang, M. (2006) Time-Satisfaction-Based Maximal Covering Location Problem. Chinese Journal of Management Science, 14, 45-51.
- Narasimhan, S., Pirkul, H. and Schilling, D.A. (1992) Capacitated Emergency Facility Siting with Multiple Levels of Backup. Annals of Operations Research, 40, 323-337. http://dx.doi.org/10.1007/BF02060485
- Lu, X.-L. and Hou, Y.-X. (2010) Allocation of Chinese National Emergency Material Depository Based on Facility Location Theory. Economic Geography, 30, 1091-1095.
- Lu, X.-L., Hou, Y.-X. and Lin, W. (2011) Functional Optimization of Emergency Medical Service Centre of Small Town Based on Facility Location Theory: A Case Study of Teng Zhou City in Shan Dong Province. Economic Geography, 31, 1119-1123.
- Lu, X.-L., Hou, Y.-X. and Lin, W. (2011) Allocation of Small-Town Emergency Material Depository Based on Location Theory: A Case Study of Fangshan District in Beijing. Geographical Research, 30, 1000-1008.
- Chen, Z.-H. and You, J.-X. (2006) A Multi-Objective Decision Model of Emergency Rescue Facility Location for Large-Scale Emergency Incidents. Management Science, 19, 10-14.
- Li, G.-Q., Zhang, J. and Liu, S.-J. (2011) Multi-Object Planning Model of Urban Emergency Logistics Facilities Location. Computer Engineering and Applications, 47, 238-241.
- Zhang, Y.-Y. (2011) Research on Location and Distribution of Multi-Objective Emergency Resources. China Safety Science Journal, 21, 153-158.
- Murali, P., Ordóñez, F. and Dessouky, M.M. (2012) Facility Location under Demand Uncertainty: Response to a Large-Scale Bio-Terror Attack. Socio-Economic Planning Sciences, 46, 78-87. http://dx.doi.org/10.1016/j.seps.2011.09.001
- Daskin, M.S. and Coullard, C.R. (2002) An Inventory-Location Model: Formulation, Solution Algorithm and Computational Results. Annals of Operations Research, 110, 83-106. http://dx.doi.org/10.1023/A:1020763400324
- Tang, K., Yang, C. and Yang, J. (2009) An Integrated Inventory-Location Model under Inflation. Chinese Journal of Management, 1, 24-30.
- Tang, K. (2008) Study on Inventory-Location for Distribution Network Design. Huazhong University of Science and Technology, Wuhan.





