ABSTRACT

In this paper, we discuss the dynamics of a stochastic SIRC epidemic model with infection rate affected by white noise. We prove that this stochastic model has a unique nonnegative solution globally. A threshold is identified. When the noise is small, the solution of the stochastic model converges to the disease-free equilibrium point of the deterministic model if $R_0^s<1$ , which means the basic reproductive number of the stochastic model. And if $R_0^s>1$ , the solution of the stochastic model fluctuates around the epidemic equilibrium of the deterministic model. When the noise is large, the disease tends to extinction. The results are illustrated by computer simulations.

Keywords:

Stochastic SIRC Model, Stability, Threshold, Persistence in Mean, The Endemic Equilibrium

1. Introduction

Mathematical models have become important instruments in the analysis and control of infectious diseases. Several models corresponding to epidemic with different characteristics have been proposed and discussed in literature [1] [2] [3] [4] [5] . The fundamental assumption in epidemic models is that the population can be divided into distinct groups; the most common are: the susceptible (S) that are the subjects that may catch the disease; the infected (I) that are the subjects that are already infected and can spread the disease to susceptible individuals; the removed (R) that are the subjects that are immune for life. Therefore, these models are referred to as SIR models.

SI, SIS, SIR models are the basic epidemic models. The differences of these models are that the population is divided into different distinct groups and the relationships between groups in these models are different. The SI model is suitable for the disease without recurrent seizures. The SIS model can describe the patient getting sick repeatedly. The SIR model is used when the patient are immunized after infection. Other descriptions may include the presence of subjects in the quarantine state (Q) and in this situation SIRQ models are analyzed [6] . The models are more and more complex with the development of epidemiology.

Recently the class of cross-immune individuals (C) in the population has been introduced [7] : it is an intermediate state between the fully susceptible state (S) and the fully protected one (R). The obtained SIRC model takes temporary partial immunity into account. The author gave a brief description of the deterministic SIRC model and calculated the basic regeneration number [8] . In 2013, Iacoviello and Stasio studied the SIRC model more closely [9] , and discussed the optimal control method in the case of the outbreak of the SIRC model based on the mathematical results.

In the study of stochastic epidemiological model, the authors give the proof of asymptotic stability of stochastic epidemic models and the theoretical results are verified by simulation experiments. The global uniqueness and asymptotic stability of the solution of the stochastic SIR model [10] were deduced in 2011. Zhao studied the stochastic SIS model in 2013 [11] , and the global uniqueness and asymptotic stability of the solution of the stochastic SIS model were deduced based on the basic regeneration number. Liu published a study of the stochastic SIRS model in 2017 [12] ; the global uniqueness and asymptotic stability of the solution of a stochastic SIRS model are deduced under the condition that the basic regeneration number is greater than 1 or less than 1.

In the existing research, there is no literature to give the basic regeneration number of stochastic SIRC model and other related characteristics. Therefore, this paper mainly studies the stochastic SIRC model, and gives the basic regeneration number of the model. It is proved that when the basic regeneration number is less than 1, the disease-free equilibrium point is randomly asymptotically stable, and when the basic regeneration number is more than 1, the solution of the stochastic model revolves around the endemic equilibrium point of the corresponding deterministic model, and computer simulation is used to verify the correctness of the conclusions.

This paper is organized as follows. We give the model description in Section 2. In Section 3, we show that there is a unique positive solution of system (2.2). In Section 4, we investigate system (2.2) is exponential stability when the noise is large. In this case, the infective decays exponentially to zero. When the noise is small, we deduce the condition $R_0^s<1$ which will enable the disease to die out exponentially in Section 4 and the condition $R_0^s>1$ for the disease being persistent is given in Section 5. In Section 6, we show that $R_0^s\ge 1$ , the result of stochastic model is asymptotically stable and is oscillating around the endemic equilibrium of the deterministic model when $t\to \infty$ . Simulations in Section 7 are reported to support the analytical results.

2. The SIRC Model

The SIRC model and its correlations between the variables are shown in Figure 1. The population can be divided into four parts.

The natural death rates of different compartments can be different for a long period. But in a short time, we can consider that the rates are the same. In this paper, we assumed that the natural death rate of S, I, R, C compartments are the same.

Here, $S\left(t\right)$ denotes the number of members who are susceptible to an infection at time t. $I\left(t\right)$ denotes the number of members who are infective to an infection at time t. $R\left(t\right)$ denotes the number of members who are immune to an infection at time t. $C\left(t\right)$ denotes the number of members who are cross-immune to an infection at time t. The parameters in the model are summarized in the following list:

A: a consistent input of new members into the population per unit time;

μ: natural death rate of S, I, R, C compartments;

β: transmission coefficient between compartments S and I;

α: transmission coefficient between compartments I and R;

ε: transmission coefficient between compartments R and C;

γ: transmission coefficient between compartments C and S.

All parameter values are assumed to be nonnegative and $0<d<1$ .

Consider the following SIRC model:

$\{\begin{array}{l}\stackrel{\dot{}}{S}=A-\mu S-\beta SI+\gamma C\\ \stackrel{\dot{}}{I}=\beta SI+d\beta CI-\left(\mu +\alpha \right)I\\ \stackrel{\dot{}}{R}=\left(1-d\right)\beta CI+\alpha I-\left(\mu +\epsilon \right)R\\ \stackrel{\dot{}}{C}=\epsilon R-\beta CI-\left(\mu +\gamma \right)C\end{array}$ (2.1)

The threshold of system (2.1) is

$R_0=\frac{\beta }{\mu +\alpha }\ast \frac{A}{\mu }$

System (2.1) always has the disease-free equilibrium:

$P_0=\left(\frac{A}{\mu },0,0,0\right)$

If $R_0>1$ , then $P_0$ is unstable and there is an epidemic equilibrium. If $R_0\le 1$ , then $P_0$ is the unique equilibrium and is globally stable in intΓ, where

$\Gamma =\left\{\left(S,I,R,C\right):S\ge 0,I\ge 0,R\ge 0,C\ge 0,S+I+R+C\le \frac{A}{\mu }\right\}$ .

In fact, epidemic models are inevitably affected by environmental white noise which is an important component in realism, because it can provide an additional degree of realism in comparison to their deterministic counterparts. Many stochastic models for epidemic population have been developed in [13] - [21] . For example, stochastic models are able to take care of randomness of infectious contacts occurring in the latent and infectious periods [22] . Dalal, Greenhalgh and Mao [20] have previously used the technique of parameter perturbation to examine the effect of environmental stochasticity in a model of AIDS and condom use. They found that the introduction of stochastic noise changes the basic reproduction number of the disease and can stabilize an otherwise unstable system. Nasell [23] formulated stochastic models to show that some stochastic models are a better approach to describe epidemics for a large range of realistic parameter values in comparison with their deterministic counterparts.

In this paper, we mainly discuss while β is affected by noise,

$\beta \to \beta +\sigma B(t)$

where $B\left(t\right)$ is standard Brownian motions with $B\left(0\right)=0$ , and with the intensity of white noise ${\sigma }^2>0$ . The stochastic version corresponding to the deterministic model (2.1) takes the following form:

$\{\begin{array}{l}\text{d}S=\left(A-\mu S-\beta SI+\gamma C\right)\text{d}t-\sigma SI\text{d}B\left(t\right)\\ \text{d}I=\left(\beta SI+d\beta CI-\left(\mu +\alpha \right)I\right)\text{d}t+\left(\sigma SI+d\sigma CI\right)\text{d}B\left(t\right)\\ \text{d}R=\left(\left(1-d\right)\beta CI+\alpha I-\left(\mu +\epsilon \right)R\right)\text{d}t+\left(1-d\right)\sigma CI\text{d}B\left(t\right)\\ \text{d}C=\left(\epsilon R-\beta CI-\left(\mu +\gamma \right)C\right)\text{d}t-\sigma CI\text{d}B\left(t\right)\end{array}$ (2.2)

3. Existence and Uniqueness of Positive Solution

In the biological dynamical system, the researcher is concerned about whether the positive solution of the system exists globally. Therefore, in this section, we show that the solution of system (2.2) is global and positive.

Theorem 3.1. There is a unique solution $\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)$ of system (2.2) on $t\ge 0$ for any initial value $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)\in {\Re }_{+}^4$ , and the solution will remain in ${\Re }_{+}^4$ with probability 1, namely $\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\in {\Re }_{+}^4$ for all $t\ge 0$ almost surely.

Proof. Since the coefficients of the equation are locally Lipschitz continuous for all given initial value $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)\in {\Re }_{+}^4$ , there is a unique local solution $\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)$ on $t\in \left(0,{\tau }_e\right)$ , where ${\tau }_e$ is the explosion time (see [24] ). To show that this solution is global, we need to show that ${\tau }_e=\infty$ , a.s. Let $k_0\ge 0$ be sufficiently large so that $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)$ lie within the interval $\left[\frac{1}{k_0},k_0\right]$ . For each integer $k\ge k_0$ , define the stopping time

$\begin{array}{l}{\tau }_k=\text{inf}\{t\in \left[0,{\tau }_e\right):\min \left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\le \frac{1}{k}\text{or}\\ \begin{array}{c}\\ \end{array}\max \left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\ge k\}\end{array}$

where throughout this paper, we set $\inf \varnothing =\infty$ (as usual $\varnothing$ donates the empty set). According to the definition, ${\tau }_k$ is increasing as $k\to \infty$ . Set ${\tau }_{\infty }={\lim }_{k\to \infty }{\tau }_k$ , whence ${\tau }_{\infty }\le {\tau }_e$ , a.s. If we can show that ${\tau }_{\infty }=\infty$ , a.s., then ${\tau }_e=\infty$ and $\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\in {\Re }_{+}^4$ , a.s. for all $t\ge 0$ . In other words, to complete the proof all we need to show is that ${\tau }_e=\infty$ , a.s. If statement is false, then there exist a pair of constants $T>0$ and $\nu \in \left(0,1\right)$ such that

$P\left({\tau }_{\infty }\le T\right)>\nu$

Hence there is an integer 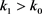such that

$P\left({\tau }_k\le T\right)\ge \nu ,k\ge k_1$ (3.1)

For $t\le {\tau }_k$ , we can see for each k

$\text{d}\left(S+I+R+C\right)=\left[A-\mu \left(S+I+R+C\right)\right]\text{d}t$

and so

$S\left(t\right)+I\left(t\right)+R\left(t\right)+C\left(t\right)=\frac{A}{\mu }+{\text{e}}^{-\mu t}\left(S\left(0\right)+I\left(0\right)+R\left(0\right)+C\left(0\right)-\frac{A}{\mu }\right)$

If $S\left(0\right)+I\left(0\right)+R\left(0\right)+C\left(0\right)\le \frac{A}{\mu }$ , then $S\left(t\right)+I\left(t\right)+R\left(t\right)+C\left(t\right)\le \frac{A}{\mu }$ , a.s. So the region

${\Gamma }^{*}=\left\{\left(S,I,R,C\right):S\ge 0,I\ge 0,R\ge 0,C\ge 0,S+I+R+C\le \frac{A}{\mu ,a.s.}\right\}$

is a positively invariant set of system (2.2) on ${\Gamma }^{*}$ , which is similar to $\Gamma$ of system (2.1). From now on, we always assume that $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)\in {\Gamma }^{*}$ .

Define a C²-function W: ${\Re }_{+}^4\to {\bar{\Re }}_{+}$ by

$W\left(S,I,R,C\right)=\left(S-1-\log S\right)+\left(I-1-\log I\right)+\left(R-1-\log R\right)+\left(C-1-\log C\right)$

The nonnegativity of this function can be seen form $u-1-\log u\ge 0,\forall u>0$ . Let $k>k_0$ and $T>0$ be arbitrary. Applying the Itô formula, we obtain

$\text{d}W=LW\text{d}t+K\text{d}B(t)$

where

$\begin{array}{c}LW=0+\left(1-\frac{1}{S}\right)\left(A-\mu SI-\beta SI+\gamma C\right)+\left(1-\frac{1}{I}\right)\left(\beta SI+d\beta CI-\left(\mu +\alpha \right)I\right)\\ +\left(1-\frac{1}{R}\right)\left(\left(1-d\right)\beta CI+\alpha I-\left(\mu +\epsilon \right)R\right)+\left(1-\frac{1}{C}\right)\left(\epsilon R-\beta CI-\left(\mu +\gamma \right)C\right)\\ +\frac{1}{2}\left\{\frac{1}{S^2}{\sigma }^2{S}^2{I}^2+\frac{1}{I^2}{\left(\sigma SI+dCI\right)}^2+\frac{1}{R^2}\left(1-d\right){\sigma }^2{C}^2{I}^2+\frac{1}{C^2}{\sigma }^2{C}^2{I}^2\right\}\\ \le A+2\beta M+\left(4\mu +\alpha +\epsilon +\gamma \right)+M^2+2{\sigma }^2{M}^2\end{array}$

$:=N$

$\begin{array}{c}K=\left(1-\frac{1}{S}\right)\sigma SI+\left(1-\frac{1}{I}\right)\left(\sigma SI+d\sigma CI\right)+\left(1-\frac{1}{R}\right)\left(1-d\right)\sigma CI+\left(1-\frac{1}{R}\right)\left(-\sigma CI\right)\\ =\left(S-1\right)\sigma I+\left(I-1\right)\sigma S+\left(I-1\right)d\sigma C+\left(1-\frac{1}{R}\right)\left(1-d\right)\sigma CI-\left(C-1\right)\sigma I\\ =\sigma I\left(S-C\right)+\left(I-1\right)\left(\sigma S+d\sigma C\right)+\left(1-\frac{1}{R}\right)\left(1-d\right)\sigma CI\end{array}$

Therefore, we get Formula (3.2)

$\begin{array}{l}E\left[W\left(S\left({\tau }_k\wedge T\right),I\left({\tau }_k\wedge T\right),R\left({\tau }_k\wedge T\right),C\left({\tau }_k\wedge T\right)\right)\right]\\ \le W\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)+E\left[{\displaystyle {\int }_0^{{\tau }_k\wedge T}N\text{d}t}\right]\\ \le W\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)+NT\end{array}$ (3.2)

Set ${\Omega }_k=\left\{{\tau }_k\le T\right\},k\ge k_1$ , and by (3.1), $P\left({\Omega }_k\right)\ge \nu$ . Note that for every $\omega \in {\Omega }_k$ , there is at least one of $S\left({\tau }_k,\omega \right)$ , $I\left({\tau }_k,\omega \right)$ , $R\left({\tau }_k,\omega \right)$ , and $C\left({\tau }_k,\omega \right)$ that equals either k or $\frac{1}{k}$ , and hence

$W\left(S\left({\tau }_k\right),I\left({\tau }_k\right),R\left({\tau }_k\right),C\left({\tau }_k\right)\right)\ge \left(k-1-\log k\right)\wedge \left(\frac{1}{k}-1+\log k\right)$

It then follows from (3.1) and (3.2) that

$\begin{array}{l}W\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)+NT\\ \ge E\left[1_{{\Omega }_k\left(\omega \right)}\ast V\left(S\left({\tau }_k\right),I\left({\tau }_k\right),R\left({\tau }_k\right),C\left({\tau }_k\right)\right)\right]\\ \ge v\left[\left(k-1-\log k\right)\wedge \left(\frac{1}{k}-1+\log k\right)\right]\end{array}$

Let $k\to \infty$ , we have

$\begin{array}{c}\infty >W\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)+NT\\ \ge E\left[1_{{\Omega }_k\left(\omega \right)}\ast V\left(S\left({\tau }_k\right),I\left({\tau }_k\right),R\left({\tau }_k\right),C\left({\tau }_k\right)\right)\right]\to \infty \end{array}$

The former formula is contradictory and we must therefore have ${\tau }_{\infty }=\infty$ , a.s.

For convenience we introduce the notation:

$\langle x\left(t\right)\rangle =\frac{1}{t}{\displaystyle {\int }_0^{t}x\left(r\right)\text{d}r}$

and

$R_0^s=\frac{\beta \frac{A}{\mu }-\frac{1}{2}{\sigma }^2{\left(\frac{A}{\mu }\right)}^2}{\mu +\gamma }$

4. Extinction

In this section, we investigate the conditions for the extinction of disease.

Theorem 4.1. Let $S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)$ be the solution of system (2) with initial value $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)\in \Gamma$ . If

(a): ${\sigma }^2\ge \frac{{\beta }^2}{2\left(\mu +\gamma \right)}$ or

(b): $R_0^s\ge 1$ and ${\sigma }^2<\frac{{\beta }^2}{2\left(\mu +\gamma \right)}$

Then $\underset{t\to \infty }{\lim }\sup \frac{\log I\left(t\right)}{t}\le 0$ , a.s.

Proof. An integration of system (2.2) yields, the Formula (4.1) is as follows

$\{\begin{array}{l}\frac{S\left(t\right)-S\left(0\right)}{t}=A-\mu \langle S\left(t\right)\rangle -\beta \langle S\left(t\right)I\left(t\right)\rangle +\gamma \langle C\left(t\right)\rangle -\frac{\sigma }{t}{\displaystyle {\int }_0^{t}S\left(r\right)I\left(r\right)\text{d}B\left(r\right)}\\ \frac{I\left(t\right)-I\left(0\right)}{t}=\beta \langle S\left(t\right)I\left(t\right)\rangle +d\beta \langle C\left(t\right)I\left(t\right)\rangle -\left(\mu +\alpha \right)\langle I\left(t\right)\rangle \\ +\frac{\sigma }{t}{\displaystyle {\int }_0^{t}S\left(r\right)I\left(r\right)\text{d}B\left(r\right)}+d\frac{\sigma }{t}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}\\ \frac{R\left(t\right)-R\left(0\right)}{t}=\left(1-d\right)\beta \langle C\left(t\right)I\left(t\right)\rangle +\alpha \langle I\left(t\right)\rangle -\left(\mu +\epsilon \right)\langle R\left(t\right)\rangle \\ -\left(1-d\right)\frac{\sigma }{t}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}\\ \frac{C\left(t\right)-C\left(0\right)}{t}=\epsilon \langle R\left(t\right)\rangle -\beta \langle C\left(t\right)I\left(t\right)\rangle +\left(\mu +\gamma \right)\langle C\left(t\right)\rangle -\frac{\sigma }{t}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B(r)}\end{array}$

Applying the Itô formula, we obtain

$\begin{array}{l}\text{d}\ln \left(I\left(t\right)\right)\\ =\left\{0+\beta S\left(t\right)+d\beta C\left(t\right)-\left(\mu +\alpha \right)+\frac{1}{2}\left(-\frac{1}{I{\left(t\right)}^2}\right){\left(\sigma S\left(t\right)I\left(t\right)+dC\left(t\right)I\left(t\right)\right)}^2\right\}\text{d}t\\ +\frac{1}{I\left(t\right)}\left(\sigma S\left(t\right)I\left(t\right)+d\sigma C\left(t\right)I\left(t\right)\right)\text{d}B(t)\end{array}$

Then Formula (4.2) is as follows

$\begin{array}{c}\frac{\ln \left(I\left(t\right)\right)-\ln \left(I\left(0\right)\right)}{t}=\beta \langle S+dC\rangle -\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2\langle {\left(S+dC\right)}^2\rangle \\ +\frac{\sigma }{t}{\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B(r)}\end{array}$

Let

$M\left(t\right):=\sigma {\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B\left(r\right)}$ ,

which is a local continuous martingale and $M\left(0\right)=0$ . Moreover

$\underset{t\to \infty }{\lim }\sup \frac{{\langle M,M\rangle }_t}{t}\le \frac{{\sigma }^2{A}^2}{{\mu }^2}<\infty$ , a.s.

According to Strong Law of Large Numbers, we obtain

$\underset{t\to \infty }{\lim }\frac{M\left(t\right)}{t}=0$ , a.s. (4.3)

Since $S\left(t\right)+I\left(t\right)+R\left(t\right)+C\left(t\right)\le \frac{A}{\mu }$ , we obtain

$\langle S+dC\rangle \le \frac{A}{\mu }$ (4.4)

Substituting (4.3) (4.4) into (4.2) yields

$\begin{array}{l}\underset{t\to \infty }{\lim }\sup \frac{\ln \left(I\left(t\right)\right)}{t}\\ =\underset{t\to \infty }{\lim }\sup (\beta \langle S+dC\rangle -\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2{\langle S+dC\rangle }^2\\ +\frac{\ln \left(I\left(0\right)\right)}{t}+\frac{\sigma }{t}{\displaystyle {\int }_0^{t}S\left(r\right)+dC\left(r\right)\text{d}B\left(r\right)})\\ \le \underset{t\to \infty }{\lim }\sup \left(\beta \langle S+dC\rangle -\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2{\langle S+dC\rangle }^2\right)\\ +\underset{t\to \infty }{\lim }\sup (\frac{\ln \left(I\left(0\right)\right)}{t}+\frac{\sigma }{t}{\displaystyle {\int }_0^{t}S\left(r\right)+dC\left(r\right)\text{d}B(r))}\end{array}$

If the condition (a) is satisfied, the following statement is tenable.

$\frac{1}{2}{\sigma }^2{\left(\frac{\beta }{{\sigma }^2}\right)}^2-\left(\mu +\gamma \right)<0$

then

$\begin{array}{l}\underset{t\to \infty }{\lim }\sup \frac{\ln \left(I\left(t\right)\right)}{t}\\ \le \underset{t\to \infty }{\lim }\sup \left(\frac{1}{2}{\sigma }^2{\left(\frac{\beta }{{\sigma }^2}\right)}^2-\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2{\langle \left(S+dC-\frac{\beta }{{\sigma }^2}\right)\rangle }^2\right)\\ \le \underset{t\to \infty }{\lim }\sup \left(\frac{1}{2}{\sigma }^2{\left(\frac{\beta }{{\sigma }^2}\right)}^2-\left(\mu +\gamma \right)\right)\le 0\end{array}$

If the conditions (b) are satisfied, Formula (4.5) can be rewritten in another way as follows

$\begin{array}{l}\underset{t\to \infty }{\lim }\sup \frac{\ln \left(I\left(t\right)\right)}{t}\\ \le \underset{t\to \infty }{\lim }\sup \left(\frac{1}{2}{\sigma }^2{\left(\frac{\beta }{{\sigma }^2}\right)}^2-\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2{\left(S+dC-\frac{\beta }{{\sigma }^2}\right)}^2\right)\\ =\left(\beta \frac{A}{\mu }-\frac{1}{2}{\sigma }^2{\left(\frac{A}{\mu }\right)}^2\right)-\left(\mu +\gamma \right)=\left(\mu +\gamma \right)\left(R_0^S-1\right)<0\end{array}$

Lemma 4.1. Let $A\left(t\right)$ and $U\left(t\right)$ be two continuous adapted increasing process on $t\ge 0$ with $A\left(0\right)=U\left(0\right)=0$ , a.s. Let $M\left(t\right)$ be a real-valued continuous local martingale with $M\left(0\right)=0$ , a.s. Let $X_0$ be a nonnegative ${\mathcal{F}}_0$ -measurable random valuable such that $E\left(X_0\right)<\infty$ . Define

$X\left(t\right)=X\left(0\right)+A\left(t\right)-U\left(t\right)+M(t)$

for all $t\ge 0$ . If $X\left(t\right)$ is nonnegative, then $\underset{t\to \infty }{\lim }A\left(t\right)<\infty$ implies that $\underset{t\to \infty }{\lim }U\left(t\right)<\infty$ , $\underset{t\to \infty }{\lim }X\left(t\right)<\infty$ , and $-\infty <\underset{t\to \infty }{\lim }M\left(t\right)<\infty$ , a.s.

Consider the equation

$x\left(t\right)=x\left(t_0\right)+{\displaystyle {\int }_{t_0}^{t}h\left(s,x\left(s\right)\right)\text{d}s}+{\displaystyle {\int }_{t_0}^{t}g\left(s,x\left(s\right)\right)\text{d}B\left(s\right)},x\in R^n,t_0\in R$

Here, $B\left(s\right)$ is an m-dimensional Brownian motion.

Lemma 4.2. Suppose that:

1) The function h and g satisfy the local Lipschitz and line growth conditions;

2) ${\sup }_{t\ge 0}\left\{E{\left|x\left(t\right)\right|}^p\right\}<\infty$ , where $\left|\cdot \right|$ is the Euclidean norm in $R^n$ .

Then almost every sample path of ${\displaystyle {\int }_{t_0}^{t}g\left(s,x\left(s\right)\right)\text{d}B\left(s\right)}$ is uniformly continuous on $t\ge 0$ .

Lemma 4.3. Let j be a nonnegative function defined on $\left[0,\infty \right)$ that is integrable on $\left[0,\infty \right)$ and uniformly continuous on $\left[0,\infty \right)$ . Then $\underset{t\to \infty }{\lim }j\left(t\right)=0$ .

Theorem 4.2. Under the condition of Theorem 4.1, the disease is extinct. And

$\underset{t\to \infty }{\lim }S\left(t\right)=\frac{A}{\mu }=S_0$ , a.s.

$\underset{t\to \infty }{\lim }I\left(t\right)=0=I_0$ , a.s.

$\underset{t\to \infty }{\lim }R\left(t\right)=0=R_0$ , a.s.

$\underset{t\to \infty }{\lim }C\left(t\right)=0=C_0$ , a.s.

Proof. By applying Itô formula to system (2.2), Formula (4.5) is established,

$\begin{array}{l}\text{d}\left[\frac{A}{\mu }-S+R+C\right]\\ =(-\mu \left(\frac{A}{\mu }-S\right)+\beta SI-\gamma C+\left(1-d\right)\beta CI+\alpha I-\left(\mu +\epsilon \right)R\\ \begin{array}{c}\\ \end{array}+\epsilon R-\beta CI-\left(\mu +\gamma \right)C)\text{d}t+\left(\sigma SI+\left(1-d\right)\sigma CI-\sigma CI\right)\text{d}B\left(t\right)\\ =\left(-\mu \left(\frac{A}{\mu }-S+R+C\right)-2\gamma C-d\beta CI+\beta SI+\alpha I\right)\text{d}t+\left(\sigma S-dC\right)I\text{d}B\left(t\right)\\ \le \left(-\mu \left(\frac{A}{\mu }-S+R+C\right)+\left(\beta S+\alpha \right)I\right)\text{d}t+\left(\sigma S-dC\right)I\text{d}B(t)\end{array}$

Then,

$\begin{array}{l}{\displaystyle {\int }_0^t\left(\frac{A}{\mu }-S\left(s\right)+R\left(s\right)+C\left(s\right)\right)\text{d}s}\\ \le \frac{A}{\mu }-S\left(0\right)+R\left(0\right)+C\left(0\right)-\mu {\displaystyle {\int }_0^{t}P\left(s\right)\text{d}s}+{\displaystyle {\int }_0^t\left(\beta S\left(s\right)+\alpha \right)I\left(s\right)\text{d}s}+Z\left(t\right)\\ \le 3\frac{A}{\mu }-\mu {\displaystyle {\int }_0^{t}P\left(s\right)\text{d}s}+{\displaystyle {\int }_0^t\left(\beta \frac{A}{\mu }+\alpha \right)I\left(s\right)\text{d}s}+Z(t)\end{array}$

where,

$Z\left(t\right)={\displaystyle {\int }_0^t\left(\sigma S\left(s\right)-dC\left(s\right)\right)I\left(s\right)\text{d}B\left(s\right)}$ and $P\left(t\right)=\frac{A}{\mu }-S\left(s\right)+R\left(s\right)+C(s)$

Obviously, we have

$0\le P\left(t\right)\le 3\frac{A}{\mu }-\mu {\displaystyle {\int }_0^{t}P\left(s\right)\text{d}s}+{\displaystyle {\int }_0^t\left(\beta \frac{A}{\mu }+\alpha \right)I\left(s\right)\text{d}s}+Z(t)$

Clearly, $\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\in {\Gamma }^{*}$ , $0<P\left(s\right)\le 2\frac{A}{\mu }$ and

$0\le \left(\beta \frac{A}{\mu }+\alpha \right)I\left(s\right)\le \left(\beta \frac{A}{\mu }+\alpha \right)\frac{A}{\mu }$ ,

so $\mu {\displaystyle {\int }_0^{t}P\left(s\right)\text{d}s}$ and ${\displaystyle {\int }_0^t\left(\beta \frac{A}{\mu }+\alpha \right)I\left(s\right)\text{d}s}$ are uniformly continuous on $\left[0,\infty \right)$ . Next, we prove that $Z\left(t\right)$ is uniformly continuous. Noting that

$\left(S\left(t\right),I\left(t\right),R\left(t\right),C\left(t\right)\right)\in {\Gamma }^{*}$ ,

we can easily check that the coefficients of system (2.2) satisfy the local Lipschitz and liner growth conditions. In addition,

$\underset{t\ge 0}{\sup }\left\{E\sqrt[p]{S^2\left(t\right)+I^2\left(t\right)+R^2\left(t\right)+C^2\left(t\right)}\right\}\le 2\frac{A}{\mu }$

Then, by lemma 4.2, $Z\left(t\right)$ is uniformly continuous. $\mu {\displaystyle {\int }_0^{t}P\left(s\right)\text{d}s}$ ,

${\displaystyle {\int }_0^t\left(\beta \frac{A}{\mu }+\alpha \right)I\left(s\right)\text{d}s}$

and $Z\left(t\right)$ are uniformly continuous, so $P\left(t\right)$ is uniformly continuous. By lemma 4.1,

$\underset{t\to \infty }{\lim }\left({\displaystyle {\int }_0^t\left(\frac{A}{\mu }-S\left(t\right)+R\left(t\right)+C\left(t\right)\right)\text{d}s}\right)<\infty$

By lemma 4.3, we obtain

$\underset{t\to \infty }{\lim }\left(\frac{A}{\mu }-S\left(t\right)+R\left(t\right)+C\left(t\right)\right)=0$

Then,

$\underset{t\to \infty }{\lim }S\left(t\right)=\frac{A}{\mu }$ a.s.

$\underset{t\to \infty }{\lim }R\left(t\right)=0$ a.s.

$\underset{t\to \infty }{\lim }C\left(t\right)=0$ a.s.

5. Persistence

Theorem 5.1. If $R_0^s>1$ and ${\sigma }^2<\frac{{\beta }^2}{2\left(\mu +\gamma \right)}$ , then for any initial value $\left(S\left(0\right),I\left(0\right),R\left(0\right),C\left(0\right)\right)\in {\Gamma }^{*}$ , the solution of system (2.2) has the following property:

$\underset{t\to \infty }{\lim }\inf \langle I\left(t\right)\rangle >0$ a.s.

Proof. From Formula (4.2), we obtain

$\begin{array}{l}\frac{\ln \left(I\left(t\right)\right)-\ln \left(I\left(0\right)\right)}{t}\\ =\beta \langle S+dC\rangle -\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2\langle {\left(S+dC\right)}^2\rangle +\frac{\sigma }{\mu }{\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B\left(r\right)}\\ =\beta \frac{A}{\mu }-\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2\langle \frac{A}{\mu }-{\left(I+R+\left(1-d\right)C\right)}^2\rangle \\ +\frac{\sigma }{t}{\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B\left(r\right)}-\beta \langle I+R+\left(1-d\right)C\rangle \end{array}$

$\begin{array}{l}=\beta \frac{A}{\mu }-\left(\mu +\gamma \right)-[\frac{1}{2}{\sigma }^2\langle {\left(\frac{A}{\mu }\right)}^2\rangle +\frac{1}{2}{\sigma }^2\langle {\left(I+R+\left(1-d\right)C\right)}^2\rangle \\ -{\sigma }^2\frac{A}{\mu }\langle I+R+\left(1-d\right)C\rangle ]+\frac{\sigma }{t}{\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B\left(r\right)}\\ -\beta \langle I+R+\left(1-d\right)C\rangle \end{array}$

From Formula (3.1), we have

$\langle I\rangle \le \frac{A}{\mu }$

$\langle R\rangle \le \frac{\left(1-d\right)\beta \frac{A}{\mu }+\alpha }{\mu +\epsilon }\langle I\rangle -\left(1-d\right)\frac{\sigma }{t\mu +\epsilon }{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}-\frac{R\left(t\right)-R\left(0\right)}{t\mu +\epsilon }$

$\langle C\rangle \le \frac{\beta \frac{A}{\mu }}{\mu +\gamma }I-\frac{C\left(t\right)-C\left(0\right)}{t\left(\mu +\gamma \right)}+\frac{\sigma }{t\left(\mu +\gamma \right)}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B(r)}$

So Formula (5.1) can be rewritten as

$\begin{array}{l}\frac{1}{2}{\sigma }^2\langle {\left(I+R+\left(1-d\right)C\right)}^2\rangle -{\sigma }^2\frac{A}{\mu }\langle I+R+\left(1-d\right)C\rangle +\beta \langle I+R+\left(1-d\right)C\rangle \\ =\beta \frac{A}{\mu }-\left(\mu +\gamma \right)-\frac{1}{2}{\sigma }^2{\left(\frac{A}{\mu }\right)}^2+\frac{\sigma }{t}{\displaystyle {\int }_0^t\left(S\left(r\right)+dC\left(r\right)\right)\text{d}B\left(r\right)}\\ -\frac{\ln \left(I\left(t\right)\right)-\ln \left(I\left(0\right)\right)}{t}\end{array}$ (5.2)

for $S\left(t\right)+I\left(t\right)+R\left(t\right)+C\left(t\right)\le \frac{A}{\mu }$ , when $t\to \infty$ , Formula (5.2) can be rewritten as

$\underset{t\to \infty }{\lim }\inf \langle I+R+\left(1-d\right)C\rangle \left[\frac{1}{2}{\sigma }^2\frac{A}{\mu }+\beta -{\sigma }^2\frac{A}{\mu }\right]>\left(R_0^S-1\right)\left(\mu +\gamma \right)>0$

$\langle I+R+\left(1-d\right)C\rangle$ can be rewritten as (5.4)

$\begin{array}{l}\langle I+R+\left(1-d\right)C\rangle =\langle I\rangle +\langle R\rangle +\left(1-d\right)\langle C\rangle \\ \le \frac{\left(1-d\right)\beta \frac{A}{\mu }+\alpha }{\mu +\epsilon }\langle I\rangle -\left(1-d\right)\frac{\sigma }{t\mu +\epsilon }{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}-\frac{R\left(t\right)-R\left(0\right)}{t\mu +\epsilon }\end{array}$

$+\frac{\beta \frac{A}{\mu }}{\mu +\gamma }\langle I\rangle -\frac{C\left(t\right)-C\left(0\right)}{t\left(\mu +\gamma \right)}+\frac{\sigma }{t\left(\mu +\gamma \right)}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}+\langle I\rangle$

Taking inferior limit of Formula (5.4), we have Formula (5.5)

$\begin{array}{l}\underset{t\to \infty }{\lim }\inf \langle I+R+\left(1-d\right)C\rangle \\ \le \left(\frac{\left(1-d\right)\beta \frac{A}{\mu }+\alpha }{\mu +\epsilon }+\frac{\beta \frac{A}{\mu }}{\mu +\gamma }+1\right)\underset{t\to \infty }{\lim }\inf \langle I\rangle \\ +\underset{t\to \infty }{\lim }\inf \left(-\left(1-d\right)\frac{\sigma }{t\mu +\epsilon }{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}-\frac{R\left(t\right)-R\left(0\right)}{t\mu +\epsilon }\right)\\ +\underset{t\to \infty }{\lim }\inf \left(-\frac{C\left(t\right)-C\left(0\right)}{t\left(\mu +\gamma \right)}+\frac{\sigma }{t\left(\mu +\gamma \right)}{\displaystyle {\int }_0^{t}C\left(r\right)I\left(r\right)\text{d}B\left(r\right)}\right)\\ \le \left(\frac{\left(1-d\right)\beta \frac{A}{\mu }+\alpha }{\mu +\epsilon }+\frac{\beta \frac{A}{\mu }}{\mu +\gamma }+1\right)\underset{t\to \infty }{\lim }\inf \langle I\rangle \end{array}$

$k\underset{t\to \infty }{\lim }\inf \langle I\rangle$

where $k\doteq \left(\frac{\left(1-d\right)\beta \frac{A}{\mu }+\alpha }{\mu +\epsilon }+\frac{\beta \frac{A}{\mu }}{\mu +\gamma }+1\right)$ , if $R_0^s>1$ , $\beta -\frac{1}{2}{\sigma }^2\frac{A}{\mu }>0$ . By substituting (5.5) into (5.3),

$\underset{t\to \infty }{\lim }\inf \langle I\left(t\right)\rangle >\frac{\left(R_0^s-1\right)\left(\mu +\gamma \right)}{k\left(\beta -\frac{1}{2}{\sigma }^2\frac{A}{\mu }\right)}$

therefore, when $R_0^s>1$ , $\underset{t\to \infty }{\lim }\inf \langle I\left(t\right)\rangle >0$ .

6. Asymptotic Property around the Epidemic Equilibrium

Consider the basic reproductive number of stochastic model $R_0^s$ , if $R_0^s<1$ , the disease becomes extinct and the solution of stochastic model converges to the disease-free equilibrium point of the deterministic model when $t\to \infty$ . Therefore, the following part is to introduce the characteristic of stochastic model when the disease survives.

Theorem 6.1. When $R_0^s\ge 1$ , the result of stochastic model is asymptotically stable and is oscillating around the endemic equilibrium of the deterministic model when $t\to \infty$ . That is

$\begin{array}{l}\underset{t\to \infty }{\lim }\sup \frac{1}{t}{\displaystyle {\int }_0^t{\left(S-S^{*}\right)}^2+{\left(I-I^{*}\right)}^2+{\left(R-R^{*}\right)}^2+{\left(C-C^{*}\right)}^2\text{d}s}\\ \le \frac{b}{\min \left(\left|a_1\right|,\left|a_2\right|,\left|a_3\right|,\left|a_4\right|\right)}\end{array}$

where

$a_1=\frac{-2\mu -\beta S^{\text{*}}+\gamma }{S^{\text{*}}}+\beta I^{\text{*}}<0$

$a_2=-\beta +\beta I^{\text{*}}-2\mu -\alpha +3\beta \frac{A}{\mu }+d\beta \frac{A}{\mu }<0$

$a_3=\left(1-d\right)\beta \frac{A}{\mu }+\left(1-d\right)\beta I^{\text{*}}+\alpha -2\left(\mu +\epsilon \right)+d\epsilon <0$

$a_4=\frac{\gamma }{S^{\text{*}}}+d\beta +\left(1-d\right)\beta I^{\text{*}}+d\epsilon -2\left(\mu +\gamma \right)<0$

$b={\sigma }^2\left(2{\left(\frac{A}{\mu }\right)}^2{I}^{\text{*}}+{\left(\frac{A}{\mu }\right)}^4\left(\frac{1}{S^{\text{*}}}+6\right)\right)$

Proof. When $R_0^s\ge 1$ , $R_0\ge 1$ . And the disease-free equilibrium $\left(S^{*},I^{*},R^{*},C^{*}\right)$ of the deterministic model satisfies following equality:

$\{\begin{array}{l}0=A-\mu S^{*}-\beta S^{*}{I}^{*}+\gamma C^{*}\\ 0=\beta S^{*}{I}^{*}+d\beta C^{*}{I}^{*}-\left(\mu +\alpha \right)I^{*}\\ 0=\left(1-d\right)\beta C^{*}{I}^{*}+\alpha I^{*}-\left(\mu +\epsilon \right)R^{*}\\ 0=\epsilon R^{*}-\beta C^{*}{I}^{*}-\left(\mu +\gamma \right)C^{*}\end{array}$

that is

$A-\mu \left(S^{*}+I^{*}+R^{*}+C^{*}\right)=0$

Define a C²-function W: ${\Re }_{+}^4\to {\bar{\Re }}_{+}$ by

$\begin{array}{c}V\left(S,I,R,C\right)=\frac{1}{S^{\text{*}}}{\left(S-S^{\text{*}}\right)}^2+{\left(I-I^{\text{*}}\right)}^2+{\left(R-R^{\text{*}}\right)}^2\\ +d{\left(C-C^{\text{*}}\right)}^2+\left(I-I^{\text{*}}-I^{\text{*}}\ln \frac{I}{I^{\text{*}}}\right)\end{array}$

by Itô formula,

$\text{d}V=LV\text{d}t+H\text{d}B\left(t\right)=\left(L{V}_1+L{V}_2+L{V}_3+L{V}_4+L{V}_5\right)\text{d}t+H\text{d}B(t)$

where

$L{V}_1=\left(I-I^{\text{*}}\right)\left(\beta S+d\beta C-\left(\mu +\alpha \right)\right)+\frac{1}{2}{\left(I^{\text{*}}\right)}^2{\left(\sigma S+d\sigma C\right)}^2$

$L{V}_2=\frac{1}{S^{\text{*}}}\left(2\left(S-S^{\text{*}}\right)\left(A-\mu S-\beta SI+\gamma C\right)+{\sigma }^2{S}^2{I}^2\right)$

$L{V}_3=2\left(I-I^{\text{*}}\right)\left(\beta SI+d\beta CI-\left(\mu +\alpha \right)I\right)+{\left(\sigma SI+d\sigma CI\right)}^2$