ABSTRACT

In this paper, we use a white noise approach to Malliavin calculus to prove the generalization of the Clark-Ocone formula

$F\left(\omega \right)=E\left[F\right]+{\displaystyle {\int }_0^T}E\left[D_{t}F\mathrm{<mo>\; |\; </mo>}{\mathcal{F}}_t\right]\diamond W\left(t\right)\text{d}t\mathrm{,}$

where $E\left[F\right]$ denotes the generalized expectation, $D_{t}F\left(\omega \right)=\frac{\text{d}F}{\text{d}\omega }$ is the (generalized) Malliavin derivative, $\diamond$ is the Wick product and $W\left(t\right)$ is the 1-dimensional Gaussian white noise.

Keywords:

White Noise, Malliavin Calculus, Wick Product, Brownian Motion

1. Introduction

In 1975, Hida introduced the theory of white noise with his lecture note on Brownian functionals [1] . After that H. Holden et al. [2] emphasized this theory with stochastic partial differential equations (SPDEs) driven by Brownian motion.

In 1984, Ocone proved the Clark-Ocone formula [3] , to give an explicit representation to integral in Itô integral representation theorem in the context of analysis on the Wiener space $\Omega =C_0\left(\left[0,T\right]\right)$ , the space of all real continuous functions on $\left[0,T\right]$ starting at 0. He proved that

$F\left(\omega \right)=E\left[F\right]+{\displaystyle {\int }_0^T}E\left[D_{t}F\mathrm{<mo>\; |\; </mo>}{\mathcal{F}}_t\right]\text{d}B\left(t\right)\mathrm{,}$ (1.1)

where $D_t$ is the Malliavin derivative and $B\left(t\right)$ is the one dimensional Brownian motion on the Winer space. In [4] the authors proved the generalization of Clark-Ocone formula (see, e.g., [5] [6] ). This theorem has many interesting application, for example, computing the replicating portfolio of call option in Black & Scholes type market. They proved that

$F\left(\omega \right)=E\left[F\right]+{\displaystyle {\int }_0^T}E\left[D_{t}F\mathrm{<mo>\; |\; </mo>}{\mathcal{F}}_t\right]\diamond W\left(t\right)\text{d}t\mathrm{,}$ (1.2)

where $E\left[F\right]$ denotes the generalized expectation, $D_{t}F\left(\omega \right)=\frac{\text{d}F}{\text{d}\omega }$ is the

(generalized) Malliavin derivative, $\diamond$ is the Wick product and $W\left(t\right)$ is the one dimensional Gaussian white noise. This formula holds for all $F\in {\mathcal{G}}^{\mathrm{<mo>\; *\; </mo>}}$ , where ${\mathcal{G}}^{\mathrm{<mo>\; *\; </mo>}}$ is a space of stochastic distribution. In particular, if $F\in L^2\left(\mu \right)$ then equation (1.2) turns out to be

$F\left(\omega \right)=E\left[F\right]+{\displaystyle {\int }_0^T}E\left[D_{t}F\mathrm{<mo>\; |\; </mo>}{\mathcal{F}}_t\right]\text{d}B\left(t\right).$

The purpose of this papper is to generalize the well known Clark-Ocone formula to generalized functions of white noise, i.e., to the space ${\mathcal{G}}^{-\beta }$ . The generalization has the following form

$F\left(\omega \right)=E\left[F\right]+{\displaystyle {\int }_0^T}E\left[D_{t}F\mathrm{<mo>\; |\; </mo>}{\mathcal{F}}_t\right]\diamond W\left(t\right)\text{d}t\mathrm{,}$

where $E\left[F\right]$ denotes the generalized expectation, $D_{t}F\left(\omega \right)=\frac{\text{d}F}{\text{d}\omega }$ is the

(generalized) Malliavin derivative, $\diamond$ is the Wick product, and $W\left(t\right)$ is the 1-dimensional Gaussian white noise.

The paper is organized as follows. In Section 2 and 3, we recall necessary definitions and results from white noise and prove a new results that we will need. Finally in Section 4, we generalize the Clark-Ocone formula, i.e., to the space ${\mathcal{G}}^{-\beta }$ .

2. White Noise

In this section we recall necessary definitions and results from white noise. For more information about white noise analysis (see e.g, [7] - [14] ).

Given $\Omega =S\left(ℝ\right)$ be the space of tempered distribution on the set $ℝ$ of real number and let $\mu$ be the Gaussian white noise probability measure on $\Omega$ such that

${\displaystyle {\int }_{\Omega }}{\text{e}}^{i\langle \omega \mathrm{,}\varphi \rangle }\text{d}\mu \left(\omega \right)={\text{e}}^{-\frac{1}{2}{\Vert \varphi \Vert }^2}\mathrm{.}$ (2.1)

where $\langle \omega \mathrm{,}\varphi \rangle$ denotes the action of $\omega \in S^{\prime }\left(ℝ\right)$ on $\varphi$ . It follows from (2.1) that

$E\left[\langle \mathrm{.,}\varphi \rangle \right]=\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}E{\left[\langle \mathrm{.,}\varphi \rangle \right]}^2={\Vert \varphi \Vert }^2\mathrm{,}\varphi \in S(ℝ)$

where $E=E_{\mu }$ denotes the expectation with respect to $\mu$ . This isometry allows us to define a Brownian motion $B\left(t\right)=B\left(t,\omega \right)$ as the continuous version of $\tilde{B}=\tilde{B}\left(t,\omega \right)=\langle \omega ,{\chi }_{\left(0,t\right)}(.)\rangle$ where

${\chi }_{\left[\mathrm{0,}t\right]}\left(s\right)=\{\begin{array}{l}\mathrm{1\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>}\text{if}\mathrm{<mi>\; </mi>\; 1}\le s\le t\mathrm{,}\\ -\mathrm{1\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>}\text{if}-t\le s\le \mathrm{0,}\\ \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{otherwise}\mathrm{.}\end{array}$

Then, $\langle \omega \mathrm{,}\phi \rangle ={\displaystyle {\int }_{ℝ}}\phi \left(t\right)\text{d}B\left(t\right)$ for all $\phi \in L^2\left(ℝ\right)$ . Let ${\mathcal{F}}_t$ be the $\sigma$ algebra generated by ${\left\{B\left(s\mathrm{,.}\right)\right\}}_{0\le s\le t}$ . If $f\left(t_1\mathrm{,}{t}_2\mathrm{,}\cdots \mathrm{,}{t}_n\right)\in {\widehat{L}}^2\left({ℝ}^n\right)$ , i.e., $f_n$ is symmetric and

${\Vert f_n\Vert }_{L^2\left({ℝ}^n\right)}={\displaystyle {\int }_{{ℝ}^n}}{f}_n^2\left(t_1\mathrm{,}\cdots \mathrm{,}{t}_n\right)\text{d}{t}_1\cdots \text{d}{t}_n<\infty \mathrm{,}$

then the iterated Itô integral is given by

${\displaystyle {\int }_{{ℝ}^n}}{f}_n\text{d}{B}^{\otimes n}\mathrm{<mo>\; :\; </mo>}=n\mathrm{<mo>\; !\; </mo>}{\displaystyle {\int }_{-\infty }^{\infty }}\left({\displaystyle {\int }_{-\infty }^{t_n}}\cdots \left({\displaystyle {\int }_{-\infty }^{t_2}}f\left(t_1\mathrm{,}\cdots ,t_n\right)\text{d}B\left(t_1\right)\right)\cdots \right)\text{d}B\left(t_n\right)\mathrm{.}$ (2.2)

In the following we let

$h_n\left(x\right)={\left(-1\right)}^n{\text{e}}^{\frac{x^2}{2}}\frac{{\text{d}}^n}{\text{d}{x}^n}\left({\text{e}}^{-\frac{x^2}{2}}\right);n=0,1,2,\cdots$ (2.3)

be the Hermite polynomials and let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be the basis of $L^2\left(ℝ\right)$ consiting

${\xi }_n\left(x\right)={\pi }^{-\frac{1}{4}}{\left(\left(n-1\right)!\right)}^{-\frac{1}{2}}{\text{e}}^{-\frac{x^2}{2}}{h}_{n-1}\left(\sqrt{2}x\right),n=1,2,\cdots$ (2.4)

The set of multi-indices $\alpha =\left({\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_n\right)$ of nonnegative integers is denoted by $T={\left({\mathbb{N}}_0^{\mathbb{N}}\right)}_{ℂ}$ . Where $\mathbb{N}=\left\{\mathrm{1,2,}\cdots \right\}$ is the set of all natural number and ${\mathbb{N}}_0=\mathbb{N}\cup \left\{0\right\}$ . If $z=\left(z_1\mathrm{,}{z}_2\mathrm{,}\cdots \right)$ is a sequence of number or function, we use the multi-induces notation

$z^{\alpha }=z_1^{{\alpha }_1}{z}_2^{{\alpha }_2}\cdots z_n^{{\alpha }_n}\text{if}\alpha =\left({\alpha }_1,\cdots ,{\alpha }_n\right)\in T$

Theorem 2.1. ( [15] ) Let ${\phi }_1\mathrm{,}{\phi }_2\mathrm{,}\cdots \mathrm{,}{\phi }_n$ be are an orthonormal function in $L^2\left(\Omega \right)$ . Then for all multi-indices $\alpha =\left({\alpha }_1\mathrm{,}\cdots \mathrm{,}{\alpha }_n\right)\in T$ , we have

${\displaystyle {\int }_{{ℝ}^{\left|\alpha \right|}}}{\phi }^{\widehat{\otimes }\alpha }\text{d}{B}^{\otimes \left|\alpha \right|}\left(x\right)=h_{{\alpha }_1}\left(\langle \omega ,{\phi }_1\rangle \right)\cdots h_{{\alpha }_n}\left(\langle \omega ,{\phi }_n\rangle \right).$

Corollary 2.2.

$\left(H_{\alpha }\diamond H_{\beta }\right)=H_{\alpha +\beta }\left(\omega \right)\mathrm{<mo>\; ;\; </mo>}\alpha \mathrm{,}\beta \in T\mathrm{.}$

where $\diamond$ denote the Wick product, and extend linearly. Then if $f_n\in {\widehat{L}}^2\left({ℝ}^n\right)\mathrm{,}{g}_n\in {\widehat{L}}^2\left({ℝ}^m\right)$ , we have

$\left({\displaystyle \sum _n}{\displaystyle {\int }_{{ℝ}^n}}{f}_n\text{d}{B}^{\otimes n}\right)\diamond \left({\displaystyle \sum _m}{\displaystyle {\int }_{{ℝ}^m}}{g}_m\text{d}{B}^{\otimes m}\right)={\displaystyle \sum _{m,n}}{\displaystyle {\int }_{{ℝ}^{m+n}}}{f}_n\widehat{\otimes }{g}_m\text{d}{B}^{\otimes \left(m+n\right)}$

Proof.

$\begin{array}{l}{\displaystyle {\int }_{{ℝ}^{\left|\alpha \right|}}}{\xi }^{\widehat{\otimes }\alpha }\text{d}{B}^{\otimes \left|\alpha \right|}\diamond {\displaystyle {\int }_{{ℝ}^{\left|\beta \right|}}}{\xi }^{\widehat{\otimes }\beta }\text{d}{B}^{\otimes \left|\beta \right|}\\ =H_{\alpha }\diamond H_{\beta }=H_{\alpha +\beta }={\displaystyle {\int }_{{ℝ}^{\left|\alpha +\beta \right|}}}{\xi }^{\widehat{\otimes }\left(\alpha +\beta \right)}\text{d}{B}^{\otimes \left|\alpha +\beta \right|}\\ ={\displaystyle {\int }_{{ℝ}^{\left|\alpha +\beta \right|}}}{\xi }^{\widehat{\otimes }\alpha }\widehat{\otimes }{\xi }^{\widehat{\otimes }\beta }\text{d}{B}^{\otimes \left|\alpha +\beta \right|}.\end{array}$

3. Stochastic Test Function and Stochastic Distribution (Konddratiev Spaces)

1) Stochastic test function spaces

Suppose $k\in \mathbb{N}$ , for $0\le \beta <1$ , let ${\left(S\right)}_{\beta }$ consist of those

$f={\displaystyle \sum _{\alpha }}{c}_{\alpha }{H}_{\alpha },$

such that

${\Vert f\Vert }_{k,\beta }={\displaystyle \sum _{\alpha }}{c}_{\alpha }^2{\left(\alpha \right)}^{1+\beta }{\left(2\mathbb{N}\right)}^{k\alpha },\forall k\in \mathbb{N},$

where

${\left(2\mathbb{N}\right)}^{k\alpha }={\displaystyle \prod _{i=1}^m}{\left(2i\right)}^{k{\alpha }_i}\mathrm{,}\text{for}\alpha =\left({\alpha }_1\mathrm{,}\cdots \mathrm{,}{\alpha }_m\right)\mathrm{.}$ (3.1)

2) Stochastic distribution

For $0\le \beta <1$ , let ${\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ be the space of Kondratiev space of stochastic distribution, consist of all formal expansions

$F={\displaystyle \sum _{\alpha }}{b}_{\alpha }{H}_{\alpha },$

such that

${\Vert F\Vert }_{-q\mathrm{,}-\beta }={\displaystyle \sum _{\alpha }}{b}_{\alpha }^2{\left(\alpha \right)}^{1-\beta }{\left(2\mathbb{N}\right)}^{-q\alpha }\mathrm{,}\text{forsome}q\in \mathbb{N}\mathrm{,}$

where ${\left(2\mathbb{N}\right)}^{\alpha }$ is defined in (3.1).

Note that ${\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ is the dual of ${\left(S\right)}_{\beta }$ and we can define the action of $F={\displaystyle {\sum }_{\alpha }}{b}_{\alpha }{H}_{\alpha }\in {\left(S\right)}_{\beta }^{*}$ on $f={\displaystyle {\sum }_{\alpha }}{c}_{\alpha }{H}_{\alpha }\in {\left(S\right)}_{\beta }$ by

$\langle F,f\rangle ={\displaystyle \sum _{\alpha }}\alpha !\left(b_{\alpha },c_{\alpha }\right),$

where $\left(b_{\alpha }\mathrm{,}{c}_{\alpha }\right)$ is the usual inner product in $ℝ$ .

Definition 3.1. Let $F\in {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ be the random variable and let $\gamma \in L^2\left(ℝ\right)$ . Then we say that F has directional derivative in the direction $\gamma$ if

$D_{\gamma }F\left(\omega \right)\mathrm{<mo>\; :\; </mo>}=\underset{ϵ\to 0}{lim}\frac{1}{ϵ}\left(F\left(\omega +ϵ\gamma \right)-F\left(\omega \right)\right)$ (3.2)

if the limit exist in $F\in {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ .

Definition 3.2. A function $\Phi \mathrm{<mo>\; :\; </mo>}ℝ\to {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ -integrable if

$\langle \Phi \left(\mathrm{.}\right)\mathrm{,}\varphi \rangle \in L^1\left(ℝ\right)\mathrm{,}\text{forall}\varphi \in {\left(S\right)}_{\beta }\mathrm{.}$

Then the ${\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ -integrable of $\Phi \left(t\right)$ , denoted by ${\displaystyle {\int }_{ℝ}}\Phi \left(t\right)\text{d}t$ , is the unique ${\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ element such that

$\langle {\displaystyle {\int }_{ℝ}}\Phi \left(t\right)\text{d}t\mathrm{,}\varphi \rangle ={\displaystyle {\int }_{ℝ}}\langle \Phi \mathrm{,}\varphi \rangle \left(t\right)\text{d}t\mathrm{,}\varphi \in {\left(S\right)}_{\beta }\mathrm{.}$

Definition 3.3. Consider $\phi \left(t\mathrm{,}\omega \right)\mathrm{<mo>\; :\; </mo>}ℝ\to {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ such that

$\phi \left(t\mathrm{,}\omega \right)\gamma \left(t\right)\text{is}\phi \left(t\mathrm{,}\omega \right)\text{-integrable}$

and

$D_{\gamma }F\left(\omega \right)\mathrm{<mo>\; =\; </mo>}{\displaystyle {\int }_{ℝ}}\phi \left(t\mathrm{,}\omega \right)\gamma \left(t\right)\text{d}t\mathrm{,\; <mi>\; </mi>}\text{forall}\mathrm{<mi>\; </mi>}\gamma \in L^2\left(ℝ\right)\mathrm{,}$

then we say that F is (Hida) Malliavin differentiable and we put

$D_{t}F\left(\omega \right):=\frac{\text{d}F}{\text{d}\omega }\left(t,\omega \right)=\phi \left(t,\omega \right),t\in ℝ.$

$D_t$ is called the Hida-Malliavin derivative or stochastic gradient of F at t.

The set of all differentiable is denoted by $\mathbb{D}$ .

Definition 3.4. Consider $F\left(\omega \right)={\displaystyle {\sum }_{\alpha }}{c}_{\alpha }{H}_{\alpha }\left(\omega \right)\in {\left(S\right)}_{\beta }^{*}$ . Then we define the stochastic derivative of F at t by

$\begin{array}{c}{D}_{t}F\left(\omega \right):=\frac{\text{d}F}{\text{d}\omega }\left(t,\omega \right):={\displaystyle \sum _{\alpha }}{c}_{\alpha }{\displaystyle \sum _i}{\alpha }_i{H}_{\alpha -{ϵ}^{\left(i\right)}}\left(\omega \right)\cdot {\xi }_i\left(t\right)\\ ={\displaystyle \sum _{\gamma }}\left({\displaystyle \sum _i}{c}_{\gamma +{ϵ}^{\left(i\right)}}\left({\gamma }_i+1\right){\xi }_i\left(t\right)\right)H_{\gamma }(\omega )\end{array}$

Lemma 3.5.

1) Let $F\in {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ . Then $D_{t}F\in {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ for a.a. $t\in ℝ$ .

2) Suppose $F\mathrm{,}{F}_m\in {\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}$ for all $m\in \mathbb{N}$ and

$F_m\to F\mathrm{<mi>\; </mi>}\text{in}\mathrm{<mi>\; </mi>}{\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{.}$

Then there exist a subsequence ${\left\{F_{m_k}\right\}}_{k=1}^{\infty }$ such that

$D_t{F}_{m_k}\to D_{t}F\mathrm{<mi>\; </mi>}\text{in}\mathrm{<mi>\; </mi>}{\left(S\right)}_{\beta }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,\; <mi>\; </mi>}\text{for}\mathrm{<mi>\; </mi>}a\mathrm{.}at>0$

Proof. 1) Suppose $F\left(\omega \right)={\displaystyle {\sum }_{\alpha }}{c}_{\alpha }{H}_{\alpha }\left(\omega \right)\in {\left(S\right)}_{\beta }^{*}$ . Then

$\begin{array}{c}{D}_{t}F\left(\omega \right)={\displaystyle \sum _{\alpha }}{c}_{\alpha }{\displaystyle \sum _i}{\alpha }_i{H}_{\alpha -{ϵ}^{\left(i\right)}}\left(\omega \right)\cdot {\xi }_i\left(t\right)\\ ={\displaystyle \sum _{\gamma }}\left({\displaystyle \sum _i}{c}_{\gamma +{ϵ}^{\left(i\right)}}\left({\gamma }_i+1\right){\xi }_i\left(t\right)\right)H_{\gamma }\left(\omega \right)\\ ={\displaystyle \sum _{\gamma }}{g}_{\gamma }\left(t\right)H_{\gamma }\left(\omega \right).\end{array}$

where $g_{\gamma }\left(t\right)={\displaystyle \sum _i}{c}_{\gamma +{ϵ}^{\left(i\right)}}\left({\gamma }_i+1\right){\xi }_i\left(t\right)\mathrm{.}$

We want to prove that for some $q\in \mathbb{N}$ ,

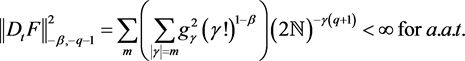
Note that

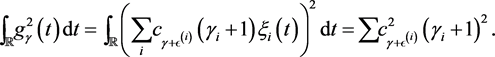
Moreover,

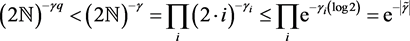
where 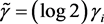for all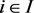. Hence,

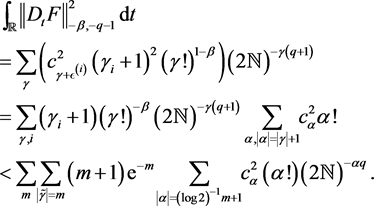
Using the fact that 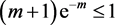for all m, we get

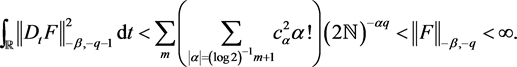(3.3)

Therefore,

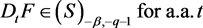
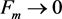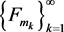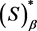2) To prove this part, it suffices to prove that if in, then there exist a subsequence such that in as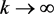, for a.a. t. We have prove that

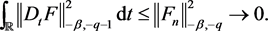
Therefore,

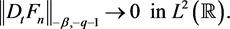
So, there exists a subsequence 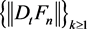such that for a.a. t as. This complete the proof.

Suppose is the Hermite functions, and put

(3.4)

and

(3.5)

and

With this notation we have, for all multi indices where.

Definition 3.6. 1) Let. We say that

belong to the space if

we define

and equip with the projective topology.

2) We say that

belong to the space if

we define

and equip with the inductive topology. Then is the dual of, with action

4. The Generalized Clark-Ocone Formula

Now we are prepared to present the main result of this paper. It generalizes the well know Clark-Ocone formula to generalized functions, i.e., to the space.

Definition 3.1. Suppose. Then the conditional expectation of F with respect to is given by

(4.1)

Note that this coincides with usual conditional expectation if, and

(4.2)

In particular

(4.3)

Lemma 4.2. Suppose. Then

Proof. Assume that, without loss of generality,

and similarly G. By Corollary 2.2 and Definition 4.1, we have

Lemma 4.3.

Let. Then for a.a..

Consider for all and

Then there exists a subsequence such that

Proof. 1) Suppose. Then

where

Choose such that. We will prove that

Note that

So

Hence, using the fact that for all n, we get

(4.4)

Therefore,

and

2) It suffices to prove that if in, then there exists a

subsequence such that in as, for a.a. t. By (4.4) we can see that in. So there exists a subsequence

such that

(4.5)

Therefore,

The last assertion follows from (4.2).

Theorem 4.4. Suppose denote Lebesque measure on. Let be -measurable. Then

and

Proof. Let be the chaos expansion of F and put

where. Then by Lemma 3.8 (see [4] ), we have

By Itô representation theorem there is a unique which is adapted and such that

and such that

since in, we conclude that

Therefore,

on the other hand, by Lemma 4.1, we have

By taking another subsequence, we obtain that

We conclude that

This completes the proof.

Lemma 4.5. Suppose and. Then

where

Proof. Let. Then

Lemma 4.6. Suppose. Then

Proof. By Lemma 4.3 and (4.4), we have

Lemma 4.7. Let and in. Then

(4.6)

Proof. In case of a complete proof is given in [4] . The proof for general is a simple modification. Note that both integral in (4.6) exist by Lemma 4.7. Hence, by Lemma 4.6 and (4.4), we have

This completes the proof.

Theorem 4.8. Let be -measurable. Then is integrable in and

where, denotes the generalized exsection of F.

Proof. Let. Then, by Lemma 3.8 (see [4] ), we have

therefore,

the limit exist in and hence in. The result follows from Lemma 4.7.

Cite this paper

Salih, M. and Jomah, S. (2018) A Generalization of the Clark-Ocone Formula. Journal of Applied Mathematics and Physics, 6, 1443-1453. https://doi.org/10.4236/jamp.2018.67121

References