Journal of Applied Mathematics and Physics
Vol.06 No.06(2018), Article ID:85267,16 pages
10.4236/jamp.2018.66101
Least Squares Hermitian Problem of Matrix Equation (AXB, CXD) = (E, F) Associated with Indeterminate Admittance Matrices
Yanfang Liang1,2, Shifang Yuan1*, Yong Tian1, Mingzhao Li1
1School of Mathematics and Computational Science, Wuyi University, Jiangmen, China
2KaiQiao Middle School in KaiPing City, Jiangmen, China
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 28, 2018; Accepted: June 11, 2018; Published: June 14, 2018
ABSTRACT
For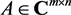 , if the sum of the elements in each row and the sum of the elements in each column are both equal to 0, then A is called an indeterminate admittance matrix. If A is an indeterminate admittance matrix and a Hermitian matrix, then A is called a Hermitian indeterminate admittance matrix. In this paper, we provide two methods to study the least squares Hermitian indeterminate admittance problem of complex matrix equation
, if the sum of the elements in each row and the sum of the elements in each column are both equal to 0, then A is called an indeterminate admittance matrix. If A is an indeterminate admittance matrix and a Hermitian matrix, then A is called a Hermitian indeterminate admittance matrix. In this paper, we provide two methods to study the least squares Hermitian indeterminate admittance problem of complex matrix equation , and give the explicit expressions of least squares Hermitian indeterminate admittance solution with the least norm in each method. We mainly adopt the Moore-Penrose generalized inverse and Kronecker product in Method I and a matrix-vector product in Method II, respectively.
, and give the explicit expressions of least squares Hermitian indeterminate admittance solution with the least norm in each method. We mainly adopt the Moore-Penrose generalized inverse and Kronecker product in Method I and a matrix-vector product in Method II, respectively.
Keywords:
Matrix Equation, Least Squares Solution, Least Norm Solution, Hermitian Indeterminate Admittance Matrices

1. Introduction
Firstly, we state some symbols that are used in this paper. The set of all real column vectors with n coordinates by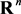 , and the set of all
, and the set of all  real matrices by
real matrices by  are denoted. Let
are denoted. Let 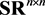 and
and 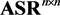 stand for the set of all
stand for the set of all 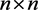 real symmetric matrices and the set of all
real symmetric matrices and the set of all 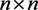 real anti-symmetric matrices, respectively. The set of all
real anti-symmetric matrices, respectively. The set of all  complex matrices is denoted by
complex matrices is denoted by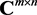 , and
, and 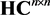 stands for the set of all
stands for the set of all 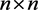 Hermitian matrices. For
Hermitian matrices. For , if the sum of the elements in each row and the sum of the elements in each column are both equal to 0, then A is called an indeterminate admittance matrix.
, if the sum of the elements in each row and the sum of the elements in each column are both equal to 0, then A is called an indeterminate admittance matrix. 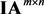 is denoted to be the set of all indeterminate admittance matrices. For
is denoted to be the set of all indeterminate admittance matrices. For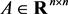 , if A is not only an indeterminate admittance matrix, but also a symmetry matrix, then A is called a symmetry indeterminate admittance matrix. Similarly, for
, if A is not only an indeterminate admittance matrix, but also a symmetry matrix, then A is called a symmetry indeterminate admittance matrix. Similarly, for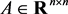 , A stands for an anti-symmetric indeterminate admittance matrix if A is an indeterminate admittance matrix and an anti-symmetric matrix.
, A stands for an anti-symmetric indeterminate admittance matrix if A is an indeterminate admittance matrix and an anti-symmetric matrix.  and
and 







where 






Definition 1 ( [1] ). For matrix



Definition 2 ( [1] ). For matrix







Definition 3 ( [1] ). For matrix






It is well known that indeterminate admittance matrices play important roles in circuit modeling and lattices network and so on [2] [3] . In this paper, we mainly discuss the least squares problem associated with indeterminate admittance matrices, and derive it as follows.
Problem I. Given





Find 

The solution 

with the least norm.
For studying Problem I mentioned above, we first state some Lemmas.
Lemma 1. ( [4] ) The matrix equation




in this case it has the general solution

where 
Lemma 2. ( [4] ) The least squares solutions of the matrix equation



where 

Direct and iterative methods on solving the matrix equations associated with the constrained matrix (such as Hermitian matrix, anti-Hermitian matrix, bisymmetric matrix, reflexive matrix) sets have been widely investigated. See [5] - [25] and references cited therein. Yuan, Liao and Lei [1] derived the least squares symmetric solution with the least norm of real matrix equation 

We now briefly introduce the contents of our paper. In Section 2, by using the Moore-Penrose generalized inverse and the Kronecker product, we derive the least squares Hermitian indeterminate admittance solution with the least norm for the complex matrix Equation (5). In Section 3, we firstly discuss a class of linear least squares problem in Hilbert inner product

2. Method I for the Solution of Problem I
In this section, we present the expression of the least square Hermitian indeterminate admittance solution of complex matrix Equation (5) with the least norm by using the Moore-Penrose generalized inverse and the Kronecker product of matrices.
Definition 4. For


Theorem 3. Suppose 


1)
where 


2)
where 


Proof. 1) For
It then follows that
Thus we have
Conversely, if the matrix 


2) For
It then follows that
Thus we have
Conversely, if the matrix 


Theorem 4. Suppose

where 


Proof. For

Thus we can get


Conversely, if the matrix 


We now consider Problem I by using the Moore-Penrose generalized inverse and Kronecker product of matrices.
Theorem 5. Given









where
where y is an arbitrary vector.
Furthermore, the unique least squares Hermitian indeterminate admittance solution with the least norm 

Proof. By Theorem 4, we can get
Thus, by Lemma 2,
By Theorem 2, it follows that
Thus we have
The proof is completed.
We now discuss the consistency of the complex matrix Equation (5). By Lemma 1 and Theorem 3, we can get the following conclusions.
Corollary 6. The matrix Equation (5) has a solution 

In this case, denote by 

Furthermore, if (16) holds, then the matrix Equation (5) has a unique solution 

In this case,

The least norm problem
has a unique solution 

3. Method II for the Solution of Problem I
The method for solving Problem I used in this section is from [26] . We concisely recall it as follows.
Definition 5. Let



1)
2)
Let


1)
2)
3)
4)
5)
6) 
Suppose






7)
8)
9)
10)
Suppose




11)
Suppose




12)
13)
Lemma 7. ( [26] ) Given matrices 


Let 

If the matrix Equation (21) is consistent, then the solution set of the matrix Equation (21) is exactly the solution set of the following consistent system

Lemma 8. ( [26] ) Given 

such that

Then the solution set of (23) is the solution set of the system (22).
We now analyze the structure of the complex matrix equation 

Let

where
Let

Note that
Let

Note that
Lemma 9. Suppose

where 

Lemma 10. Suppose

where 

Lemma 11. Suppose

where 


Theorem 12. Suppose









where 

1)
2) Let
Thus


3) Let
Thus


Proof. 1)
2) By (1), Definition 5 and Lemma 7, we can get
3) The proof is similar to that of (2), so we omit it.
The proof is completed.
We now use Lemmas 7 - 11, and Theorem 12 to consider the least squares Hermitian indeterminate admittance solution for the matrix Equation (5). The following notations and lemmas are necessary for deriving the solutions.
For






where
Theorem 13. Let










where y is an arbitrary vector.
Furthermore, the unique least squares Hermitian indeterminate admittance solution with the least norm 

Proof. By Theorem 4, we can get
Then by Lemma 11, the least squares problem
with respect to the Hermitian indeterminate admittance matrix X is equivalent to the following consistent matrix equation
Thus, by Lemma 2, 
From Lemma 11, it follows that
where y is an arbitrary vector. it yields that
The proof is completed.
We now discuss the consistency of the complex matrix Equation (5). By Lemma 1 and Theorem 13, we can get the following conclusions.
Corollary 14. The matrix Equation (5) has a solution 

In this case, denote by 

where y is an arbitrary vector.
Furthermore, if (39) holds, then the matrix Equation (5) has a unique solution 

In this case,

The least norm problem
has a unique solution 

4. Conclusion
In this paper, we mainly consider the least squares Hermitian indeterminate admittance problem of the complex matrix equation


Funding
The research is supported by Natural Science Foundation of China (No. 11571220), Guangdong Natural Science Fund of China (No. 2015A030313646), and the Characteristic Innovation Project (Natural Science) of the Education Department of Guangdong Province (No. 2015KTSCX148).
Cite this paper
Liang, Y.F., Yuan, S.F., Tian, Y. and Li, M.Z. (2018) Least Squares Hermitian Problem of Matrix Equation (AXB, CXD) = (E, F) Associated with Indeterminate Admittance Matrices. Journal of Applied Mathematics and Physics, 6, 1199-1214. https://doi.org/10.4236/jamp.2018.66101
References
- 1. Yuan, S.-F., Liao, A.-P. and Lei, Y. (2007) Least Squares Symmetric Solution of the Matrix Equation with the Least Norm. Mathematica Numerica Sinica, 29, 203-216. (In Chinese)
- 2. Elena, A.S., Carlos, C.P. and Teresa, M.M. (2017) Equivalent Circuits for Nonsymmetric Reciprocal Two Ports Based on Eigenstate Formulation. IEEE Transactions on Microwave Theory and Techniques, 65, 4812-4822. https://doi.org/10.1109/TMTT.2017.2708103
- 3. Haigh, D.G., Clarke, T.J.W. and Radmore, P.M. (2006) Symbolic Framework for Linear Active Circuits Based on Port Equivalence Using Limit Variables. IEEE Transactions on Circuits and Systems I, 53, 2011-2024. https://doi.org/10.1109/TCSI.2006.882815
- 4. Ben-Israel, A. and Greville, T.N.E. (1974) Generalized Inverses: Theory and Applications. John Wiley and Sons, New York.
- 5. Chen, J.-L. and Chen, X.-H. (2001) Special Matrices. Qinghua University Press, Beijing. (In Chinese)
- 6. Dehghan, M. and Hajarian, M. (2014) Finite Iterative Methods for Solving Systems of Linear Matrix Equations over Reflexive and Anti-Reflexive Matrices. Bulletin of the Iranian Mathematical Society, 40, 295-323.
- 7. Dehghan, M. and Hajarian, M. (2013) Construction of an Efficient Iterative Method for Solving Generalized Coupled Sylvester Matrix Equations. Transactions of the Institute of Measurement and Control, 35, 961-970. https://doi.org/10.1177/0142331212465105
- 8. Dehghan, M. and Hajarian, M. (2012) Iterative Algorithms for the Generalized Centro-Symmetric and Central Anti-Symmetric Solutions of General Coupled Matrix Equation. Engineering Computations, 29, 528-560. https://doi.org/10.1108/02644401211235870
- 9. Dehghan, M. and Hajarian, M. (2012) Solving Coupled Matrix Equations over Generalized Bisymmetric Matrices. International Journal of Control, Automation and Systems, 10, 9005-9012. https://doi.org/10.1007/s12555-012-0506-2
- 10. Dehghan, M. and Hajarian, M. (2012) On the Generalized Reflexive and Anti-Reflexive Solutions to a System of Matrix Equations. Linear Algebra and Its Applications, 437, 2793-2812. https://doi.org/10.1016/j.laa.2012.07.004
- 11. Dehghan, M. and Hajarian, M. (2011) The (R, S)-Symmetric and (R, S)-Skew Symmetric Solutions of the Pair of Matrix Equations and . Bulletin of the Iranian Mathematical Society, 37, 273-283.
- 12. Hajarian, M. and Dehghan, M. (2011) The Generalized Centro-Symmetric and Least Squares Generalized Centro-Symmetric Solutions of the Matrix Equation AYB + CYTD = E. Mathematical Methods in the Applied Sciences, 34, 1562-1579. https://doi.org/10.1002/mma.1459
- 13. Hernández, V. and Gassó, M. (1989) Explicit Solution of the Matrix Equation AXB-CXD = E. Linear Algebra and Its Applications, 121, 333-344. https://doi.org/10.1016/0024-3795(89)90708-8
- 14. Liao, A.-P., Bai, Z.-Z. and Lei, Y. (2006) Best Approximate Solution of Matrix Equation AXB + CYD = E. SIAM Journal on Matrix Analysis and Applications, 27, 675-688. https://doi.org/10.1137/040615791
- 15. Liao, A.-P. and Lei, Y. (2005) Least Squares Solution with the Mininum-Norm for the Matrix Equation . Computers & Mathematics with Applications, 50, 539-549. https://doi.org/10.1016/j.camwa.2005.02.011
- 16. Magnus, J.R. (1983) L-Structured Matrices and Linear Matrix Equations. Linear and Multilinear Algebra, 14, 67-88. https://doi.org/10.1080/03081088308817543
- 17. Mansour, A. (2010) Solvability of in the Operators Algebra B(H). Lobachevskii Journal of Mathematics, 31, 257-261. https://doi.org/10.1134/S1995080210030091
- 18. Hajarian, M. (2014) Matrix form of the CGS Method for Solving General Coupled Matrix Equations. Applied Mathematics Letters, 34, 37-42. https://doi.org/10.1016/j.aml.2014.03.013
- 19. Mitra, S.K. (1977) The Matrix Equation . SIAM Journal on Applied Mathematics, 32, 823-825. https://doi.org/10.1137/0132070
- 20. Peng, Z.-Y. and Peng, Y.-X. (2006) An Efficient Iterative Method for Solving the Matrix Equation . Numerical Linear Algebra with Applications, 13, 473-485. https://doi.org/10.1002/nla.470
- 21. Sheng, X.-P. and Chen, G.-L. (2010) An Iterative Method for the Symmetric and Skew Symmetric Solutions of a Linear Matrix Equation . Journal of Computational and Applied Mathematics, 233, 3030-3040. https://doi.org/10.1016/j.cam.2009.11.052
- 22. Shi, S.Y. and Chen, Y. (2003) Least Squares Solution of Matrix Equation AXB + CXD = E. SIAM Journal on Matrix Analysis and Applications, 24, 802-808. https://doi.org/10.1137/S0895479802401059
- 23. Tian, Y.-G. (2000) The Solvability of Two Linear Matrix Equations. Linear and Multilinear Algebra, 48, 123-147. https://doi.org/10.1080/03081080008818664
- 24. Wang, Q.-W. and He, Z.-H. (2013) Solvability Conditions and General Solution for Mixed Sylvester Equations. Automatica, 49, 2713-2719. https://doi.org/10.1016/j.automatica.2013.06.009
- 25. Xu, G.-P., Wei, M.-S. and Zheng, D.-S. (1998) On Solutions of Matrix Equation AXB + CXD = F. Linear Algebra and Its Applications, 279, 93-109. https://doi.org/10.1016/S0024-3795(97)10099-4
- 26. Yuan, S.-F. and Liao, A.-P. (2014) Least Squares Hermitian Solution of the Complex Matrix Equation AXB + CXD = E with the Least Norm. Journal of the Franklin Institute, 351, 4978-4997. https://doi.org/10.1016/j.jfranklin.2014.08.003
















































