Received 9 May 2016; accepted 10 June 2016; published 13 June 2016

ABSTRACT

Although many studies have found a kind of a relationship between an Epstein-Barr Virus (EBV) and the development of Multiple Sclerosis (MS), a fundamental aspect of this relationship remains uncertain. What is the cause of Multiple Sclerosis (MS)? In this study, we re-analysed the data as published by Wandinger et al. and were able to establish a new insight: without an Epstein-Barr Virus (EBV) infection no development of Multiple Sclerosis (MS). Furthermore, we determined a highly significant causal relationship between Epstein-Barr Virus (EBV) and multiple sclerosis. Altogether, Epstein-Barr Virus (EBV) is the cause of multiple sclerosis (p-value 0.0004251570).

Keywords:

Epstein Barr Virus, Multiple Sclerosis

1. Introduction

Multiple Sclerosis (MS) is an unpredictable disease of the central nervous system which disrupts the communication between the brain and other parts of the body. Multiple Sclerosis (MS) can range from relatively benign to somewhat disabling and devastating symptoms. Some of today approved drugs to treat multiple sclerosis include Novantrone (mitoxantrone), teriflunomide, dimethyl fumarate, copolymer I (Copaxone) and forms of beta interferon. Steroids are used to reduce the duration and severity of attacks in some patients suffering from multiple sclerosis. Exercise and physical therapy can help to preserve remaining function. Various aids such as foot braces, canes, and walkers are of use to help patients to remain independent and mobile. Thus far, there is as yet no cure for multiple sclerosis while millions of people are suffering from this many times deadly disease.

Epstein-Barr Virus (EBV), a herpes virus, is a primary cause of Infectious Mononucleosis (IM) and associated with several malignancies including such as Hodgkin lymphoma, non-Hodgkin lymphoma, Burkitt lymphoma and other. Epidemiological, molecular virology and other [1] - [6] studies have been able to establish EBV as a risk factor for the development of Multiple Sclerosis (MS) and provided some evidence that the pathogenesis of multiple sclerosis might involve a response to an EBV infection. Still, the cause of Multiple sclerosis is not identified.

2. Material and Methods

2.1. Definitions

Definition. Bernoulli random variable

Let 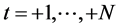denote an individual Bernoulli trial each with constant success probability p. Let N denote the number of independent Bernoulli trials (the size of a random sample or of the population).

Definition. The 2 × 2 table

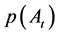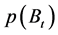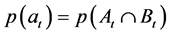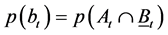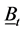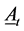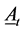Let A_t denote a Bernoulli/Binomial distributed random variable. Let denote the probability of A_t. Let B_t denote a Bernoulli/Binomial distributed random variable. Let denote the probability of B_t. Let denote joint distribution of A_t and B_t. Let denote joint distribution of A_t and. Let denote joint distribution of and B_t. Let denote joint distribution of and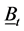. In general, it is. Thus far, the relationships before are expressed in the 2 × 2 table (Table 1).

Thus far, let 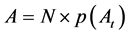denote the expectation value. Let 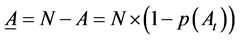denote the expectation value. Let 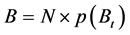denote the expectation value. Let denote the expectation value. Let denote the expectation value. Let denote the expectation value. Let denote the expectation value. Let denote the expectation value. Let denote the size of the sample or the size of the population. Let denote the expectation value of the condition (i.e. a risk factor, the verum population, the exposed group). Let denote the expectation value of the non-condition (i.e. the non-exposed group, the control population). Let denote the expectation value of the conditioned. Let denote the expectation value of the not conditioned. Thus far, the relationships before are expressed in the 2 × 2 table (Table 2).

Definition. Risk ratio or relative risk

Various quantitative techniques are used in Biostatistics to the describe and evaluate relationships among biologic and medical phenomena. Relative risk, defined by Fischer [7] as ψ, is an important [8] [9] statistical method used in epidemiologic studies and clinical trials. Let RR(A, B) denote the relative risk. Based on the 2 by 2 table above, the relative risk RR(A, B) is defined as

(1)

In epidemiology and statistics, Relative Risk (RR) is the ratio of the probability of an event a occurring under conditions of being exposed to (a + b), the non-exposed to the probability of c occurring under conditions of being exposed to (c + d), the non-exposed group. The Relative Risk (RR) is a widely used measure of association in epidemiology. A risk ratio RR(A, B) < 1 suggest that an exposure can be considered as being associated with a reduction in risk. A risk ratio RR(A, B) > 1 suggest that an exposure can be considered as being associated with an increase in risk.

Conditions

The following relationships are taken with friendly permission by Ilija Barukčić [10] .

Definition. Conditio sine qua non relationship

Let denote [10] the extent to which a condition A is a conditio sine qua non of the conditioned B. The conditio sine qua non relationship is calculated as

(2)

The relationship before is expressed in the following 2 × 2 (Table 3).

Definition. Anti conditio sine qua non relationship

Let denote [10] the extent to which a condition A is not a conditio sine qua non of the conditioned B. The anti conditio sine qua non relationship is calculated as

(3)

The relationship before is expressed in the following 2 × 2 table (Table 4).

Definition. Conditio per quam relationship

Let denote [10] the extent to which a condition A is a conditio per quam of the conditioned B. The conditio per quam is calculated as

(4)

The relationship before is expressed in the following 2 × 2 table (Table 5).

Definition. Anti conditio per quam relationship

Let denote [10] the extent to which a condition A is not a condition per quam of the conditioned B. The anti conditio per quam relationship is calculated as

(5)

The relationship before is expressed in the following 2 × 2 table (Table 6).

Definition. Conjunction. A and B relationship

Let denote [10] the extent to which a condition A is conjugated with the conditioned B. The conjunction is calculated as conjunction of the two events

(6)

The relationship before is expressed in the following 2 × 2 table (Table 7).

Definition. Exclusion relationship

Let denote [10] the extent to which a condition A excludes the conditioned B and vice versa. The exculsion relationship (the Sheffer stroke) named after Henry M. Sheffer is written as a vertical bar or an upwards arrow and calculated as

(7)

or

(8)

The relationship before is expressed in the following 2 × 2 table (Table 8).

Definition. Disjunction. A or B relationship

Let denote [10] the extent to which the condition A or the conditioned B are given. The inclusive disjunction also known as alternation is calculated as

(9)

or

(10)

The relationship before is expressed in the following 2 × 2 table (Table 9).

Definition. Neither A nor B relationship

Let denote [10] the extent to which neither a condition A nor the conditioned B is given. The neither A nor B relationship was introduced by Charles Sanders Peirce and is known also as Peirce’s arrow too and can be calculated as

(11)

The relationship before is expressed in the following 2 × 2 table (Table 10).

Definition. Equivalence of A and B relationship

Let denote [10] the extent to which a condition A and the conditioned B are equivalent. The equivalence of A and B is calculated as

(12)

The relationship before is expressed in the following 2 × 2 table (Table 11).

Definition. Either A or B relationship

Let denote [10] the extent to which either the condition A or the conditioned B is given. The either A or B relationship can be calculated as

(13)

The relationship before is expressed in the following 2 × 2 table (Table 12).

2.2. Material

Patients and Samples

Data and material for this re-analysis were published by Wandinger [11] et al., a study specifically designed to investigate the relation between Multiple Sclerosis (MS) and viral infections. Wandinger et al. examined sera from a large cohort of 163 healthy control subjects (control group) and 108 patients with a diagnosis of clinically definite multiple sclerosis for the presence of human herpes viruses type 1 (HSV-1), HSV-2, cytomegalovirus (CMV) and EBV by the presence of IgG antibodies. In addition, other investigations (i.e. the detection of EBV DNA in all serum samples) were performed. Some of the data of Wandinger et al. data about the prevalence of IgG antibodies in serum samples from Multiple Sclerosis (MS) patients and healthy control subjects are summarized in the table shown below (Table 13).

The data of the prevalence of IgG antibodies in serum samples from multiple sclerosis (MS) patients and healthy control subjects are viewed in the following 2 × 2 table (Table 14).

2.3. Methods

2.3.1. The Chi-Squared Distribution

The properties of the chi-squared distribution were first investigated by Karl Pearson [12] in 1900. The chi- squared distribution is a widely used probability distributions in hypothesis testing [14] , inferential statistics (Table 15) or in construction of confidence intervals.

In last consequence, the Chi Square with one degree of freedom is nothing but the distribution of a single normal deviate squared.

2.3.2. The Binomial Proportion Confidence Interval

The statistical significance of deviations from a theoretically expected distribution of observations can be tested

by a binomial test. For large samples, the binomial distribution is well approximated by convenient Pearson’s chi-squared test. The above relationships are grounded on the assumption, that the number of successes X out of a sample of n observations is equal to X = N. In general, let denote the degrees of freedom 1 of the f-distribution for the lower confidence bound. Thus far, it is. Under conditions where N = X the proportion of success is, the is then. Let denote the degrees of freedom 2 of the f-distribution for the lower confidence bound. In particular, we obtain. Under conditions where N = X the proportion of success is and. The exact one-sided lower confidence interval with confidence level 1 − alpha for the proportion of successes can be calculated [13] as

(14)

Example.

Given a sample proportion p and sample size N we can test claims about the population proportion p₀. Different hypothesis tests and test methods (binomial test, one-sample z-test, the t statistic et cetera) can be used to determine whether a hypothesized population proportion p₀ differs significantly from an observed sample proportionp. A hypothesis test requires that a null hypothesis and an alternative hypothesis are mutually exclusive. That is, if a null hypothesis is true, the alternative hypothesis must be false and vice versa. How can we conduct a hypothesis test of a proportion. Especially under conditions, where an observed sample proportion p is equal to 1, the F distribution [13] is of use for these purposes. Thus far, the proportion of successes of our sample above is equal to. Assuming an alpha = 0.05 level of significance the F-value should be calculated as provided above. The F-value for X = N = 271 (Alpha = 0.05) is . The exact one-sided lower confidence bound for the proportion of successes follows as

(15)

In other words, we assume that the p in the population is greater or equal to 0.989006512. Furthermore, the one- sided lower confidence interval with confidence level 1 − alpha for the proportion of successes, reflects a significance level of i.e. alpha = 0.05, and can be calculated for N > 50 approximately [13] as

(16)

A 100 ´ (1 − alpha)% confidence interval consists of all those values for which a test of the hypothesis is not rejected at a significance level of 100 ´ (alpha)%.

2.3.3. Causal Relationship k

The mathematical formula of the causal relationship k was used to determine the cause-effect relationship between Epstein-Barr Virus (EBV) infections and Multiple Sclerosis (MS). According to Barukčić [14] , the causal relationship k is calculated as

(17)

The relationship before is expressed in the following 2 × 2 table (Table 16).

Pearson’s chi-squared test X²

(18)

is used to evaluate how likely it is that the observed causal relationship k arose by chance. The 2 × 2 contingency table is dichotomous while the statistical X² distribution is continuous. Thus far, Pearson’s chi-square test tends to make results larger than they should be and is biased upwards on this account. This upwards bias of Pearson’s chi-square test can be corrected by using Yates correction.

Scholium.

As a response to Yules association of two attributes Karl Pearson introduced the mean square contingency [15] into statistics as

(19)

Still, Pearson failed to derive a mathematical formula of the causal relationship k and much more than this. Pearson himself exterminated any kind causation from statistics ultimately. Following Pearson, “We are now in a position, I think, to appreciate the scientific value of the word cause. Scientifically, cause… is meaningless…” [14] . According to Pearson, the words cause and effect belong strictly to the sphere of sense-impressions. Thus far, “there is… no true cause and effect” [14] . The reader can hardly fail to have been impressed that Pearson himself denies any kind of causality. In the first place, there is no causation at all. “No phenomena are causal” [14] . Finally, “The wider view of the universe sees all phenomena as correlated, but not causally related” [14] . Consequently, Pearson demands that “… there is association but not causation” [14] . We have now reached some very important conclusions about Pearson’s account for causality. Due to Pearson, there is no causation at all. Thus far, neither Pearson’s correlation coefficient nor his mean square contingency can be regarded as the mathematical formula of the causal relationship k. In particular, Pearson failed to derive and to provide a self-consistent mathematical proof of a mathematical formula of the causal relationship.

2.3.4. Statistical Analysis

Data were analyzed using Microsoft Excel version 14.0.7166.5000 (32-Bit) software (Microsoft GmbH, Munich, Germany). The mathematical formula of the causal relationship k [14] and the chi-square distribution [12] were applied to determine the significance of causal relationship between EBV and multiple sclerosis (MS). A p value of <0.05 was considered significant.

3. Results

3.1. Clinical Characteristics

Wandinger [11] et al. examined 108 MS patients from the Department of Neurology (University of Lübeck School of Medicine). All patients were examined independently by two neurologists and had a diagnosis of clinically definite MS. Kurtzke’s functional systems and Expanded Disability Status Scale (EDSS) were used to grade the physical disability.

3.2. EBV Seropositivity

The viral status was classified by following serologic definitions. Wandinger [11] et al. defined primary EBV infection by positivity of anti-EA-IgG and/or anti-EA-IgM in the absence of anti-EBNA-1 antibodies. A latent or past EBV infection was defined by positivity of anti-EBNA-1 antibodies. A reactivation of a latent EBV infection was defined by EBNA-1-IgG-positive individuals by additional positive anti-EA-IgG and anti-EA-IgM or additional high anti-EA-IgM. The marker for latent EBV infection was defined by an anti-EBV nuclear antigen type 1 (anti-EBNA-1) immunoglobulin (Ig)G antibodies.

3.3. Epstein Barr Virus (EBV) Is a Conditio Sine Qua Non of Multiple Sclerosis (MS)

A hypothesis test is used to distinguish between the null hypothesis and the alternative hypothesis.

Theorem 1.

Null hypothesis: EBV is a conditio sine qua non of multiple sclerosis (MS) (p₀ ≥ p).

Alternative hypothesis: EBV is not a conditio sine qua non of multiple sclerosis (MS) (p₀ < p).

Significance level (Alpha) below which the null hypothesis will be rejected: 0.05.

Proof by a statistical hypothesis test.

The data of the prevalence of IgG antibodies in serum samples from Multiple Sclerosis (MS) patients and healthy control subjects are viewed in the following 2 × 2 table (Table 17).

The proportion of successes of the condition sine qua non relationship in the sample or the test statistic can be calculated defined before as

(20)

The critical value p_lower is calculated approximately as

(21)

The critical value p_lower = 0.989006512 and is less than the proportion of successes as obtained from the observations (significance level alpha = 0.05).

Conclusio.

We cannot reject the null hypothesis in favor of the alternative hypotheses. The sample data do support the Null hypothesis that Epstein Barr Virus (EBV) is a conditio sine qua non of Multiple Sclerosis (MS).

In other words, without an infection with Epstein Barr Virus (EBV) no development of multiple sclerosis (MS).

Quod erat demonstrandum.

3.4. Epstein Barr Virus (EBV) Is the Cause of Multiple Sclerosis (MS)

Theorem 2.

Conditions.

Alpha level = 5%.

The two tailed critical Chi square value (degrees of freedom = 1) for alpha level 5% is 3.841458821.

Claims.

Null hypothesis (H₀): k = 0 (No causal relationship).

There is no causal relationship between Epstein Barr virus (EBV) and multiple sclerosis (MS).

Alternative hypothesis (H_A): k ¹ 0 (Causal relationship).

There is a significant causal relationship between Epstein Barr virus (EBV) and multiple sclerosis (MS).

Proof by two sided hypothesis test.

Based on the data (Table 18) of Wandinger et al., we compute the causal relationship k(EBV, MS)_Obtained (our test statistic) as

(22)

Following Barukčić, the test statistics obtained is equivalent with a X² value of

(23)

A two tailed Chi square of 11.2664020209 is equivalent to a p-value of 0.0004251570.

Conclusio.

The value of the test statistic (k obtained or Chi square calculated) is 11.2664020209 and exceeds the critical Chi square value of 3.841458821. Consequently, we reject the null hypothesis (H₀) and accept the alternative hypothesis (H_A).

There is a highly significant causal relationship between Epstein Barr virus (EBV) and multiple sclerosis (k = +0.2038956576, p-value 0.0004251570).

Quod erat demonstrandum.

4. Discussion

Today, the etiology of Multiple Sclerosis (MS) is largely unknown but Multiple Sclerosis (MS) is rare among individuals without serum EBV antibodies. Thus far, there is an accumulating literature for a role of Epstein- Barr Virus (EBV) infections in the pathogenesis of Multiple Sclerosis (MS). Especially, several epidemiological studies suggested an association between infection with Epstein-Barr Virus (EBV) and the occurrence of Multiple Sclerosis (MS) disease. In particular, a recent large prospective epidemiological study showed a relationship between an increase of serum antibody titres against EBV before onset of MS. Acherio et al. [16] conducted a prospective, nested case-control study of 62,439 women participating in the Nurses’ Health Study to determine whether elevation in serum antibody titers to EBV precede the occurrence of Multiple Sclerosis (MS). Acherio et al. concluded that EBV is associated with the etiology of multiple sclerosis. Recently, Levin et al. [17] conducted a study among more than 3 million US military personnel and found a relationship between EBV infection and development of MS. Apart from these and other studies aiming at the aetiology of multiple sclerosis (MS), the cause of Multiple Sclerosis (MS) has still not been identified.

We conducted a re-analysis of the study of Wandinger [11] et al. to re-investigate the role between EBV infection and MS disease. Using some of the data obtained by the study of Wandinger et al., we questioned whether Epstein-Barr Virus (EBV) is the cause or a cause of multiple sclerosis (MS). The study of Wandinger et al. was properly constructed. In accordance with previous studies, Wandinger et al. found an unexpectedly high seropositivity rate in MS patients for EBV compared with control subjects. Wandinger et al. observed an association of the EBV with MS but failed to detect the true meaning of Epstein-Barr virusin the pathogenesis of multiple sclerosis (MS).

In addition, our study confirms a conditio sine qua non relationship between EBV infection and Multiple Sclerosis (MS). In other words, without an infection with Epstein-Barr Virus (EBV) no development of Multiple Sclerosis (MS) (significance level alpha = 0.05). We observed a highly significant causal relationship between Epstein-Barr Virus (EBV) and multiple sclerosis (k = +0.203895658, p value = 0.000425157). A particular aspect of our study is the identification of Epstein-Barr Virus (EBV) as the cause of multiple sclerosis. Since without an infection by Epstein-Barr Virus (EBV) no multiple sclerosis develops and due to the fact that there is a highly significant causal relationship between Epstein-Barr Virus (EBV) and multiple sclerosis, we are allowed to deduce that Epstein-Barr Virus (EBV) is not only a cause but the cause of Multiple Sclerosis (MS).

5. Conclusion

A particular aspect of our study is the identification of Epstein-Barr Virus (EBV) as the cause of Multiple Sclerosis (MS). Finally, the cause of multiple sclerosis is identified. Consequently, it is more than necessary to develop a low-cost and highly effective vaccine against Epstein-Barr Virus (EBV).

Cite this paper

Katarina Barukčić,Ilija Barukčić, (2016) Epstein Barr Virus—The Cause of Multiple Sclerosis. Journal of Applied Mathematics and Physics,04,1042-1053. doi: 10.4236/jamp.2016.46109

References