Journal of Applied Mathematics and Physics
Vol.04 No.05(2016), Article ID:66665,6 pages
10.4236/jamp.2016.45098
Nature of the Quantum Potential
Anton Lipovka
Centro de Investigacion en Fisica, Universidad de Sonora, Sonora, Mexico

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2016; accepted 20 May 2016; published 23 May 2016
ABSTRACT
In this paper we suggested a natural interpretation of the de Broglie-Bohm quantum potential, as the energy due to the oscillating electromagnetic field (virtual photon) coupled with moving charged particle. Generalization of the Schrödinger equation is obtained. The wave function is shown to be the eigenfunction of the Sturm-Liouville problem in which we expand virtual photon to include it implicitly into consideration. It is shown that the non-locality of quantum mechanics is related only with virtual photon. As an example, the zero-energy of harmonic oscillator is obtained from classical equations.
Keywords:
Quantum Potential, de Broglie-Bohm Interpretation, Beables, Hidden Variables, the Meaning of the Wave Functions

1. Introduction
Interpretation of quantum theory (both classical and relativistic) since its birth to the present day is the subject of much debate on the fundaments of quantum physics. At first glance, the situation is reassuring, because now we have dozen different formulations of quantum theory [1] and can apply these powerful techniques for computing. However, there are a number of unresolved fundamental issues showing us that we do misunderstand something in the meaning of these formulations and we still do not have a final interpretation of quantum theory.
It is well known, the Bohmian formulation based on Louis de Broglie’s pilot-wave theory suggests particularly a great conceptual advantage in possible interpretation because it is causal and not local. Finally it leads to the complete Hamilton function that contains the quantum potential, which reflects fundamental properties of nature (see [2] - [5] and references therein).
The quantum potential plays a central role in the formalism of Bohm and is used in modern physics and theoretical chemistry. It is of great importance because on the one hand the Bohmian formulation and quantum potential allows us to better understand the foundations, and fundamentals of theory. On the other hand quantum potential has multiples practical applications in different fields of knowledge (for example in the solid state physics, in theoretical chemistry etc.) because it gives us an opportunity to simulate different quantum effects without the involvement of the wave functions of system, and without solving the Schrödinger equation. In this case, the Monte Carlo method is applied to the hydrodynamic calculations, which are sometimes the only possibility to get the result, when the Schrödinger equation cannot be solved exactly.
Unfortunately up to now we did not understand clearly the nature of quantum potential and wave functions. This problem on the one hand provokes many speculations and strange hypothesis, but on the other hand this misunderstanding makes it difficult to progress in important areas such as quantum computers, solid state and many others. These fundamental questions were debated by many authors from the beginning of quantum theory. As an example we quote here the paper [1] : “Schrödinger invented this formulation in hope of casting quantum mechanics into a “congenial” and “intuitive” form―he was ultimately distressed when he found that his wavefunctions were functions in configuration space and did not actually exist out in ordinary three-dimensional space.” and also: “The wavefunction should be regarded as a mathematical tool for calculating the outcomes of observations, not as a physically present entity existing in space…”
As it was mentioned above, this misunderstanding provokes many strange and exotic ideas and papers, where quantum potential is used for speculations, particularly in cosmology to construct the most intrigue entity- cosmological constant. For this reasons it is of great importance to reveal physical sense and nature of quantum potential, and to determine the specific role of the wave function in the formalism of quantum mechanics.
Recently the paper [6] was published, in which a new foundation had been proposed to unify the quantum theory and relativity. In this paper it was shown that quantization naturally appeared as consequence of geometrical properties of our Universe, and Planck’s constant was just adiabatic invariant of the electromagnetic field, determined by the Riemann-Cartan geometry (i.e. by the Hubble’s and the cosmological constants). It was constructed self-consistent non-local quantum theory based on Einstein’s generalized theory of gravity in the Riemann-Cartan manifold. It should be stressed that this theory does not requires any initial assumptions, external to the theory and alien by nature. So, we need not any axioms, wave functions or hidden variables.
Another paper in which a natural origin of quantization was suggested was published by Garcia-Morales [7] . In this work the quantization of the action S was obtained as a consequence of thermodynamic theory (i.e. also without artificial axiomatic constructions).
These results also suggest that the orthodox formulations of quantum theory [1] based on the axiom of the wave function existence are not complete and should be reconsidered.
In present paper the quantum potential is shown to be formed by bounded electromagnetic field-virtual photon (see section 3 for details), which is a principle part and main participant for any bounded quantum system.
2. Enigma of Quantum Potential
Usually quantum potential in the Bohmian formulation of quantum theory is defined this way (we consider here one-particle case because that for many particles is treated the same manner). Schrödinger equation is
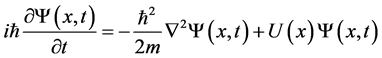 . (1)
. (1)
Writing the wave function in form 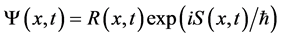 we immediately obtain two equations:
we immediately obtain two equations:
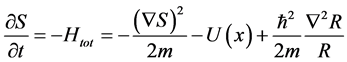 (2)
(2)
and
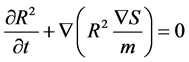 . (3)
. (3)
The first one is a Hamilton-Jacobi equation written for a modified Hamiltonian:
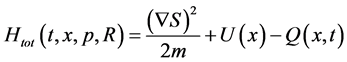 (4)
(4)
where 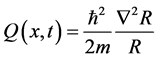 is so-called quantum potential, and second one is a continuity equation written for
is so-called quantum potential, and second one is a continuity equation written for
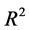 . This modified Hamiltonian usually named as
. This modified Hamiltonian usually named as ―dependent one, and additional term (the quantum potential) usually interpreted as “an internal energy associated with a certain region of phase space, absent in classical mechanics, but arising in quantum mechanics from the uncertainty principle” [2] . It is difficult to agree with this point of view for many reasons. First of all note that the discussed system, described by Equation (1) is supposed to be isolated one, but it does not contains any variable electromagnetic field. Instead, it contains an artificial quantum potential.
―dependent one, and additional term (the quantum potential) usually interpreted as “an internal energy associated with a certain region of phase space, absent in classical mechanics, but arising in quantum mechanics from the uncertainty principle” [2] . It is difficult to agree with this point of view for many reasons. First of all note that the discussed system, described by Equation (1) is supposed to be isolated one, but it does not contains any variable electromagnetic field. Instead, it contains an artificial quantum potential.
It is clear, our system should contain an oscillating electromagnetic field produced by electron, but we do not see it in Equation (1). At the same time the Bohmian formulation has the following features:
・ there is presence of hidden variables (it should be treated as a hint for presence of bounded electromagnetic field);
・ it is causal (so, it should be a classical field theory);
・ not local (presence of an electromagnetic field in theory).
Taking into account the fact that the only real substance we have in our arsenal to capture experimental events is electromagnetic field (this is an experimental fact), we can conclude that this field we lost in the beginning. This “lost” field was found in [6] and now we are able to identify quantum potential with that bounded non-local classical electromagnetic field mentioned above.
3. Nature Does Not Have Hidden Variables
Recently [8] the idea was suggested that quantum potential appears due to a “concealed” motion. Namely author show that in the case when our system consist of two parts, one of which is characterized by observable coordinates 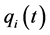 and other one has “concealed” coordinates
and other one has “concealed” coordinates 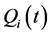 (here we use notations of author), the Hamilton function of such a system can be shown to contain quantum potential, which “may be regarded as the kinetic energy of additional concealed freedoms” [8] . But the Lagrangian used by author is incomplete (see Equation (1.1) in [8] ), so to begin with we need to write correct action for our system.
(here we use notations of author), the Hamilton function of such a system can be shown to contain quantum potential, which “may be regarded as the kinetic energy of additional concealed freedoms” [8] . But the Lagrangian used by author is incomplete (see Equation (1.1) in [8] ), so to begin with we need to write correct action for our system.
Action of the system under consideration one can write as:
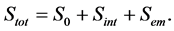 (5)
(5)
Here 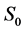 is action for particle(s) without electromagnetic field,
is action for particle(s) without electromagnetic field,
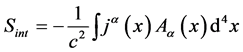 (6)
(6)
is the interaction between electromagnetic field and charge(s), and
 (7)
(7)
is action for electromagnetic field. It can be seen that both 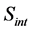 and
and 
It should be stressed here, the Bohmian formulation is non-relativistic one by origin, so we may restrict our speculation by non-relativistic case. Let us consider the hydrogen atom as an example, where to simplicity sake we believe
The classical energy equation for our reduced classical system 




Here integration is carried out over 4-volume, and Hamiltonian 




Here we sum only over n, and index 



These expressions actually are complete “quantum” non-local (integrated over the photon volume) equations to describe our system in Minkowsky space, with clearly written non-local hidden variables (beables) of the virtual photon (which are the coefficients


From this relation we immediately obtain the Hamilton-Jacobi Equation (2) written for a complete Hamiltonian of our system (4), where “quantum potential” now has clear sense and must be attributed to presence of the virtual photon (electromagnetic “pilot-wave”). As to the continuity Equation (3) written for


where


To conclude this part it should be useful to make some comments on the Hamilton-Jacobi Equation (2)

Now, when the physical sense of “quantum potential” (as classical potential that corresponds to the oscillating electromagnetic field with energy

is zero). In this case we obtain a classical system with classical Hamilton function 
4. Discussion
Very fundamental and at the same time useful example suggests harmonic oscillator. We have discussed it from this point of view before in [6] , but it would be interesting to discuss it briefly in the context of the proposed interpretation of the quantum potential. It should be done the same way as it was made in previous part (see eq. (5)-(15)). The Hamiltonian written for harmonic oscillator is:

Substituting coherent state wave function 

which should be recognized as energy of virtual photon in zero-state of harmonic oscillator (remember here the frequency of electron oscillations is the same that has the virtual photon). So, the total Hamilton function for “quantum” (in reality classical) harmonic oscillator in ground state is

with the oscillation frequency of electron (and virtual photon)
One can see again―the total Hamilton function corresponds to the complete mechanical system classical by nature which does not contain the hidden variables. And so called “quantum potential” appears due to the presence of virtual photon with frequency

In light of these results it becomes immediately obvious meaning of Bell’s theorem, as a classical statement about the impossibility of motions with a speed faster than light in the framework of the relativistic theory.
5. Conclusions
Conclusions of our work can be formulated as follows:
1) The quantum potential is shown to be an additional energy, electromagnetic by origin, which appears due to the presence of coupled harmonic electromagnetic field (virtual photon).
2) The wave functions are shown to be just a complete basis of the Sturm-Liouville problem (written for reduced system with action
3) It is stressed that the non-locality of quantum mechanics is related only with this virtual photon, namely with distribution of harmonic electromagnetic field in the system under consideration.
Cite this paper
Anton Lipovka, (2016) Nature of the Quantum Potential. Journal of Applied Mathematics and Physics,04,897-902. doi: 10.4236/jamp.2016.45098
References
- 1. Styer, D.F., Balkin, M.S., Becker, K.M., Burns, M.R., Dudley, C.E., Forth, S.T., Gaumer, J.S., Kramer, M.A., Oertel, D.C., Park, L.H., Rinkoski, M.T., Smith, C.T. and Wotherspoon, T.D. (2002) Nine Formulations of Quantum Mechanics. American Journal of Physics, 70, 288-297.
- 2. Dennis, G., de Gosson, M.A. and Hiley, B.J. (2015) Bohm’s Quantum Potential as an Internal Energy. Physics Letters A, 379, 1224-1227.
- 3. Riggs, P.J. (2008) Reflections on the deBroglie-Bohm Quantum Potential. Erkenntnis, 68, 21-39.
- 4. Esposito, S. (1999) Photon Wave Mechanics: A De Broglie-Bohm Approach. Foundations of Physics Letters, 12, 533-545.
http://dx.doi.org/10.1023/A:1021643108407 - 5. Grössing, G. (2009) On the Thermodynamic Origin of the Quantum Potential. Physica A, 388, 811-823.
http://dx.doi.org/10.1016/j.physa.2008.11.033 - 6. Lipovka, A. (2014) Planck Constant as Adiabatic Invariant Characterized by Hubble’s and Cosmological Constants. Journal of Applied Mathematics and Physics, 2, 61-71.
http://lanl.arxiv.org/abs/1401.2404
http://dx.doi.org/10.4236/jamp.2014.25009 - 7. Garcia-Morales, V. (2015) Quantum Mechanics and the Principle of Least Radix Economy. Foundations of Physics, 45, 295-332. http://dx.doi.org/10.1007/s10701-015-9865-x
- 8. Holland, P. (2015) Quantum Potential Energy as Concealed Motion. Foundations of Physics, 45, 134-141.
http://dx.doi.org/10.1007/s10701-014-9852-7 - 9. Ginzburg, V. (1987) Theoretical Physics and Astrophysics. Pergamon Press, Oxford.


