Journal of Applied Mathematics and Physics
Vol.04 No.03(2016), Article ID:65106,22 pages
10.4236/jamp.2016.43059
High-Order Finite Difference Schemes for the First Derivative in Von Mises Coordinates
S. O. Alharbi*, M. H. Hamdan
Department of Mathematical Sciences, University of New Brunswick, Saint John, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 January 2016; accepted 26 March 2016; published 29 March 2016
ABSTRACT
Third- and fourth-order accurate finite difference schemes for the first derivative of the square of the speed are developed, for both uniform and non-uniform grids, and applied in the study of a two-dimensional viscous fluid flow through an irregular domain. The von Mises transformation is used to transform the governing equations, and map the irregular domain onto a rectangular computational domain. Vorticity on the solid boundary is expressed in terms of the first partial derivative of the square of the speed of the flow in the computational domain, and the schemes are used to calculate the vorticity at the computational boundary grid points using up to five computational domain grid points. In all schemes developed, we study the effect of coordinate clustering on the computed results.
Keywords:
Von Mises Transformation, Non-Uniform Grid, Coordinate Clustering

1. Introduction
Fluid flow through irregular geometries (that is, geometries that do not conform to known coordinate lines) is encountered in many natural and industrial phenomena. Natural occurrences include flow in channels and in rivers over the curvilinear channel bottom, flow into a dam with a curvilinear free-surface, and groundwater and oil flow through the curvilinear earth layers and reservoirs. Industrial applications of flow through irregular domains include flow of air over wings and streamlined bodies, flow in curvilinear ducts, pipes and conduits, flow through turbines and propeller systems, and flow through artificial human and animal tissues, [1] . Solutions to, and analysis of initial and boundary value problems are important in the above-mentioned processes, and many involve solving the Navier-Stokes equations.
The inherent difficulty in solving the Navier-Stokes equations analytically encouraged the use of the more flexible numerical techniques to obtain approximate, yet accurate, solutions to initial and boundary value problems. The method of finite differences proved to be a flexible approach to a large number of flow problems, and has extensively been used due to its simplicity. This method has become an indispensable tool in the numerical treatment of initial and boundary value problems in Mathematical Physics, and its use in the simulation of two- and three-dimensional fluid flow problems is well-documented and frequently reported in the fluid dynamics literature, (cf. [1] - [4] and the references therein). Promotion of the status of finite differences as a means of producing accurate numerical solutions to fluid flow problems in general domains has been advanced by the introduction of grid-generation and the multi-grid method (cf. [1] and the references therein), while its utility in simulating flow in complex and curvilinear geometries has been advanced by the introduction of domain decomposition and coordinate transformation techniques (cf. [1] [2] [4] - [7] and the references therein).
In solving boundary value problems that involve viscous fluid flow in two space dimensions, the Navier- Stokes equations are usually cast in vorticity-streamfunction form. The streamfunction possesses Dirichlet conditions if the solid boundary is assumed to be a streamline of the flow. However, no explicit expression exists for the vorticity on a solid boundary. This forces one to impose a Neumann (derivative) boundary condition on the vorticity. Neumann boundary condition is derived using the definition of the vorticity as the Curl of the velocity vector, [2] [8] [9] . Vorticity at the solid boundary therefore remains a quantity to be solved for. Accurate computation of boundary vorticity has a great influence on the local and global accuracies of the numerical solution of quantities in the flow domain. Furthermore, local accuracy of the computation of boundary vorticity affects the overall global accuracy of the numerical schemed used. This emphasizes the urgent need of accurately computing the vorticity at the boundary [8] .
In order to capture the boundary effects more accurately, the use of non-uniform grid with grid clustering at the boundary proved to be a viable tool. Grid refinement has been extensively studied and widely used, and a fairly large number of algebraic and mapping methods have been proposed to produce grid clustering for any given boundary shape, [4] [5] [7] [10] [11] . However, grid clustering also produces unfavourable effects on the convergence and the global accuracy of numerical solution obtained. These effects are due in part to the altering of the coefficient matrix that represents the finite difference form of the governing equations, and the potential loss of diagonal dominance of the coefficient matrix, [8] [11] . Additionally, non-smoothness characteristics of non-uniform grid have been shown to adversely affect the performance of the numerical scheme employed [7] .
In order to overcome the above shortcomings, forward and backward finite difference schemes of various orders of local accuracy continue to be developed to better capture the boundary effects (including better approximation to the vorticiy on a solid boundary), [12] . A large number of research articles has dealt with the testing of high order (although mainly second- and third-order) schemes when a non-uniform grid is employed (cf. [4] , [6] [7] [11] [13] [14] and the references therein). However, there does not seem to exist a consensus as to which scheme or what order is best. The governing Navier-Stokes equations are usually approximated using second- order central differencing schemes. It has been argued (cf. [8] and the references therein) that a higher-order scheme for the vorticity on the solid wall may better approximate the vorticity there, however at the expense of a deteriorating and unstable solution to the governing equations.
The above conclusion has been reached for the case of uniform grid. However, many authors have reached a similar conclusion when a non-uniform grid is used, and some, [14] , emphasized that the accuracy of the solution to the governing equations depends on the order of the scheme and on other factors such, as the stretching parameters employed, the error tolerance used in the solution methodology, and the iterative procedure employed. In addition, oscillations in the solutions have been pointed out by Pandit, Kalita and Dalal, [14] , who stated that “For fourth-order approximation of the vorticity at boundary points, some spurious oscillations were observed. When third-order approximation was used for the same, initially slight oscillations were seen.”
Various authors emphasized that discarding schemes due to their low order of accuracy are “premature” when a non-uniform grid is used, (cf. [6] [12] and the references therein), and they argue that low order schemes may “have a lesser impact on the loss of diagonal dominance”. Agarwal, [8] , expressed a similar point of view for the case of uniform grid, where a “first-order scheme for the vorticity at a solid wall may have lesser impact on deteriorating the accuracy of the numerical solution to the governing Navier-Stokes equations”.
In summary, computation of boundary vorticity accurately is tantamount to finding a most suitable finite difference expression for the first derivative of the tangential velocity component; one that minimizes the unfavourable effects on the coefficient matrix and one that produces the best approximation to the boundary vorticity, whether one employs a uniform or a non-uniform grid.
In the case of fluid flow in curvilinear domains, the domain is first mapped onto a rectangular domain (or a regular domain) where finite differences can be applied. Numerical solution is then sought for transformed governing equations and boundary conditions, [1] [5] - [7] [9] [12] [15] [16] . In particular, the vorticity Neumann boundary condition is transformed into the new coordinate system and a suitable differencing scheme is employed to accurately approximate the boundary vorticity. Numerical approximation to the boundary vorticity is influenced by a number of factors, including:
- The type of grid and spacing used.
- Entry condition (say to a channel).
- The use of flow-field grid points.
In order to shed some light on the above factors, Awartani, Ford and Hamdan, [16] , and Siyyam,Ford and Hamdan, [14] , considered the flow of a viscous fluid in a two-dimensional curvilinear channel. The curvilinear physical domain is mapped onto a rectangular computational domain using the von Mises coordinates, [1] [5] [15] [16] , and the governing equations and boundary conditions are cast in von Mises variables. Vorticity condition on the physical boundary is expressed in terms of the first derivative of the square of the speed of the flow on the boundary of the transformed plane. Their use of the von Mises coordinates reduces the effects of non-smoothness in coordinate clustering. This is due to the fact that when a uniform grid is chosen in the physical domain, use of the von Mises transformation produces a naturally smooth clustered grid in the computational domain. In the above previous work, [12] [16] , schemes of first-, second- and third-order local accuracy were developed for the first derivative and used in the calculation of vorticity on the flow domain boundary. In those schemes, stencils involving up to five computational grid points were used, and a comparison was offered between uniform and non-uniform grids. Evaluation of vorticity at a single corner point in the flow domain (where the exact solution is known) demonstrated the superiority of non-uniform grid when the von Mises transformation is used.
The above reported previous work, [5] [16] , however, remained silent about the use of schemes of higher- order local accuracy, and the impact of using clustering in the physical domain on the computed vorticity on the boundary. This motivates the current work in which we develop and validate finite difference expressions, for the first derivative, that can be used in the accurate evaluation of vorticity on the flow domain boundary. Ultimately, finite difference expressions that yield the best approximation for the vorticity on the boundary are recommended for implementation in the full numerical solution of the channel flow problem described in this work. The intention is to develop a fourth-order scheme of local accuracy to approximate the vorticity on the boundary for both uniform and non-uniform grids using five grid-point stencils, and to address the following points when transforming a curvilinear physical domain into a rectangular computational domain:
- The type of grid spacing used: Typically, clustered grid near the boundary is expected to produce more accurate results. However, in some coordinate transformation procedures there are factors limiting how “compacted” the grid points can be. An important question to ask is whether a uniform grid in the computational domain can produce a clustered grid in the physical domain.
- Entry conditions to a channel: In case of a uniform entry condition to a channel, there is a correspondence between a grid in the computational domain and a grid in the physical domain, in the sense that clustering in the physical plane produces the same clustering in the computational domain. However, when a more realistic parabolic entry profile is used, the correspondence is lost and the use of clustered grid becomes necessary in the computational domain. We will consider the effects of a parabolic entry profile when the von Mises transformation is used with both uniform and non-uniform grids.
- Use of interior grid points in the approximation: A question that needs to be answered is how many internal grid points should be used in approximating the vorticity on the boundary, and how far from the boundary can grid points be taken for uniform and clustered grids. This work will demonstrate that a natural order of grid points that are closest to the boundary result in more accurate approximations to boundary vorticity.
In order to present our procedures and report the findings of this study, this work is organized as follows. In the following sections, we present a formulation of the problem of viscous fluid flow in a two-dimensional curvilinear configuration and transform the governing equations into von Mises variables. We present a discretization of the computational domain and derive third and fourth order accurate standard finite difference schemes for the first derivative and we test these schemes on a uniform grid and four clustered grids.
2. Problem Formulation
2.1. The Physical Domain
We consider a physical problem that gives rise to the need for finite difference expressions for the first derivative. Non-uniform grid arises in a number of ways, including clustering of coordinates and where coordinate transformation is involved. In the current work we consider the von Mises transformation which gives rise to the need for non-uniform grid.
Consider the flow in a two-dimensional, symmetric, dimensionless channel bounded below and above by solid, curvilinear boundaries. The channel is shown in Figure 1, and is described by: 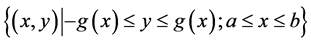 where
where 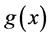 is a known smooth function.
is a known smooth function.
The flow of a viscous, incompressible fluid through the channel is governed by the equations of continuity and linear momentum, which take the following dimensionless forms, respectively, (cf. [9] [16] ):
 (1)
(1)
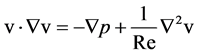 (2)
(2)
wherein, for two-dimensional flow, 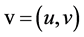 is the velocity vector field, p is the pressure, Re is the Reynolds number,
is the velocity vector field, p is the pressure, Re is the Reynolds number, 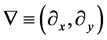 ,
, 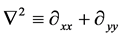 , and subscript notation denotes partial differentiation. Equations (1) and (2) represent a system of three scalar equations that are to be solved for the primitive variables u(x,y), v(x,y), and p(x,y), subject to the no-slip velocity condition on the solid lower and upper boundaries. At the inlet and exit of the channel, the normal velocity component vanishes, that is
, and subscript notation denotes partial differentiation. Equations (1) and (2) represent a system of three scalar equations that are to be solved for the primitive variables u(x,y), v(x,y), and p(x,y), subject to the no-slip velocity condition on the solid lower and upper boundaries. At the inlet and exit of the channel, the normal velocity component vanishes, that is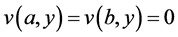 , while the tangential velocity component, u, can be taken as a function of y (assuming the channel is long enough to allow for this condition to be imposed at the exit).
, while the tangential velocity component, u, can be taken as a function of y (assuming the channel is long enough to allow for this condition to be imposed at the exit).
The dimensionless continuity Equation (1) implies the existence of a dimensionless streamfunction, 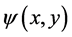 , such that:
, such that:
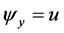 (3)
(3)
and
 . (4)
. (4)
Elimination of the pressure term from Equation (2) and the introduction of the dimensionless vorticity 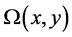 that is defined in terms of the velocity components as
that is defined in terms of the velocity components as
Figure 1. Representative sketch: physical domain.
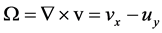 (5)
(5)
facilitate casting the flow equations in the following vorticity-streamfunction form:
Streamfunction equation:
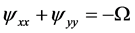 (6)
(6)
Vorticity equation:

In vorticity-streamfunction, the problem has been reduced from that of solving three equations in three primitive variables to that of solving two equations in the two unknowns 

Appropriate boundary and inlet conditions are the no-slip on the upper and lower walls of the channel, and a parallel, parabolic inlet profile at x = a. We assume that the channel is of sufficient length so that inlet and exit conditions are the same, namely:



The absence of explicit vorticity boundary conditions necessitates imposing appropriate inlet, exit and solid boundary conditions. Assuming that Equation (5) is valid on all boundaries then, with





Along the lower and upper boundaries, respectively, we have:



In order to solve Equations (6) and (7), subject to conditions (9a)-(9d), numerically using finite differences, the flow domain is first transformed into a rectangular domain using the von Mises coordinates, and the governing equations and boundary conditions are cast in von Mises variables. The von Mises transformation and the transformed governing equations and boundary conditions are discussed in what follows.
2.2. The Computational Domain and Von Mises Transformation
Consider the curvilinear net 



The Jacobian of transformation is given by

If


Second partial derivative operators can be obtained by applying operators (12) and (13) onto themselves.
Applying the above transformation to the vorticity-streamfunction Equations (6) and (7), respectively, yields, [9] [10] [16] :


where

The problem has thus been transformed from that of solving Equations (6) and (7) for 





on the lower boundary 
on the upper boundary 
at both inlet and exit 

at inlet and exit, and on the lower and upper boundaries
The square of the speed of the flow is given by:

and the velocity components are expressed as


Clearly, vorticity condition on the solid upper and lower channel boundary is given by (17d) in terms of the first derivative of the square of the speed of the flow. In the process of solving Equations (14) and (15) numerically, subject to conditions (17), we need to develop finite difference formulas for the first derivative in (17d).
Figure 2. The transformed computational domain.
3. Finite Difference Expressions for the First Derivative
3.1. Discretizing the Flow Domain
The rectangular computational domain of Figure 2 is discretized using either a uniform grid or a clustered grid, with vertical grid lines ranging from I = 1 at x = a to I = Imax at x = b, and horizontal grid lines ranging from j = 1
at the lower computational boundary 

It has been shown, [16] , that if a uniform grid is fitted over the computational domain, the corresponding gridlines in the physical domain would be clustered away from the boundary and closer to the center of the channel. However, in order to capture the effects of boundary conditions more accurately, it is required to have the clustering near the boundary.
Clustering of grid lines near the computational boundary when the von Mises variables are used can be accomplished in two ways:
1) Selecting a uniform grid in the physical domain and calculating the grid spacing in the computational domain results in a “natural” clustering near the computational boundary. For the given parabolic inlet velocity profile, and the indicated range of streamlines, we can choose y to vary over the interval [−1,1], and calculate the step size 



three variable grid spacings in the computational domain, corresponding to a uniform grid in the physical domain with




2) Selecting a grid in the physical domain that is non-uniform and clustered near the physical boundary produces a computational grid that is also clustered near the computational boundary.
Physical grid clustering can be accomplished in various ways, including the use of elementary functions. For the current work, we employ the square root, the cubic root and the square functions to define the clustering in the physical y-direction. These are illustrated in Tables 1-5, wherein we provide a comparison with the case of uniform grid in the physical domain (Table 1) and the case of uniform grid in the computational domain (Table 5) with
3.2. Calculating Square of the Speed at Inlet
At the inlet to the channel, the computational velocity conditions are:



Table 1. Grid 1. Uniform grid in the physical domain 

Table 2. Grid 2. Non-uniform grid in the physical domain. 

Table 3. Grid 3. Non-uniform grid in the physical domain. 

Table 4. Grid 4. Non-uniform grid in the physical domain. 

Table 5. Grid 5. Uniform grid in the computational domain with
Using (20), we compute 
Table 6. Square of the speed at inlet to computational domain for the five grids used.
3.3. Derivation of Finite Difference Schemes
The definition of vorticity is expressed at the lower boundary of the computational domain, in von Mises coordinates as the following derivative of the square of the speed of the flow:

In order to obtain finite difference expressions for
In order to derive forward differencing schemes of local accuracy n for the first derivative along the grid line (i,1) using 

where E is the local truncation error. The weights, 



where

The coefficients, 

where


For uniform grid, 

Using (23) in (22), and equating to zero the coefficients of the first n partial derivatives (including the zero’th derivative) of 




The order of the leading error term, E, will be the coefficient of 

Based on the above description, Siyyam, Ford and Hamdan, [12] , observed the following:
1) The relationship between the order of the scheme, n, and the minimum number, k, of grid points used is that


2) The number of standard schemes that use k = n + 1 grid points when 
given by the combination:
3) If
4) If
The above observations are used to construct Table 7, below, that gives the number of possible schemes when 
3.4. Derivation of Standard Fourth-Order Accurate Scheme
We employ the procedure above to derive a standard fourth-order accurate scheme (that is, n = 4) using five grid points. We thus take
Table 7. Number of possible standard schemes corresponding to

or equivalently

coefficients 

The leading local truncation error has the following leading term that is the coefficient of

Equations (32) translate into the following five equations in the five coefficients:

Solution to this system of 5 equations in 5 unknowns is given by





where




For the four types of non-uniform grids given in Tables 1-4, the values of 
Using (40)-(43) in (35)-(39), coefficients 






For uniform grid with step size h, coefficients 

and the fourth-order expression for the first derivative takes the form:
Table 8. Values of 

Values of the coefficients 
3.5. Standard Third-Order Accurate Schemes
In order to arrive at a third-order (n = 3) locally accurate forward differencing scheme for the first derivative, Awartani, Ford and Hamdan, [16] , used the above procedure and employed four grid points (
Letting

then the coefficients satisfy the following conditions:

Equations (52) represent a determinate system consisting of 4 equations in 4 unknowns that has the following unique solution:

where
Table 9. Values of coefficients 

and

The leading error term, 

The four standard, third-order accurate schemes that use the four grid points j = 1, 2, 3 and 4, are as follows:
(1,2,3,4) Scheme:
Solution (53), above, provides the following expression that was initially derived by Awartani, Ford and Hamdan, [3] :

where

For uniform grid, (57) yields the following scheme:

Values of the coefficients 
Other standard third-order accurate schemes obtained in this work employ grid points 
Table 10. Values of coefficients of the (1,2,3,4) scheme.
the form given by (52), with coefficients
(1,2,3,5) Scheme:

where

For uniform grid, (59) yields the following scheme:

Values of the coefficients 
(1,2,4,5) Scheme:

where
Table 11. Values of coefficients of the (1,2,3,5) scheme.

For uniform grid, (62) yields the following scheme:

Values of the coefficients 
(1,3,4,5) Scheme:

where

For uniform grid, (65) yields the following scheme:

Table 12. Values of coefficients of the (1,2,4,5) scheme.
Values of the coefficients 
3.6. Standard First- and Second-Order Accurate Schemes
Six standard, second-order accurate schemes have been developed by Awartani, Ford and Hamdan, [16] , using combinations of grid points on the boundary and the four grid points closest to the boundary. Henceforth, the notation 

(1,2,3) Scheme:

where

For uniform grid, (3.49) reduces to the following second-order accurate formula:

Combinations of standard first-order schemes that use the two grid points 



For the sake of comparison of results, we list below the natural order (1,2)-scheme that produced the most accurate results in [12] :
(1,2)-Scheme:

For uniform grid, (72) reduces to:

Table 13. Values of coefficients of the (1,3,4,5) scheme.
4. Results and Discussion
An expression for the vorticity on the lower computational channel boundary is given by



In order to approximate

the schemes developed in this work. These values are computed on the uniform and non-uniform grids given in Tables 1-5, using the square of the speed values of Table 6.
In the following Tables, we list the computed values of 

Comparison of the schemes that use the natural order of grid points in conjunction with the five grids used, is given in Table 14. This table demonstrates that the fourth order accurate scheme produces a corner vorticity that is closest to the exact value, with a Percentage Relative Error of 0.125% when Grid 3 is used. The fourth order accurate scheme consistently produces lower Percentage Relative Error for all of the grids employed.
Standard, first-order accurate scheme of Equation (72) produces the results in Table 14, below, which shows that using Grid 3 produces the most accurate computed values of vorticity and least Percentage Relative Errors. This may be ascribed to the fact that Grid 3 uses grid points that are closest to the boundary, hence better able to capture boundary effects. Grid 5 (uniform grid) produces the least accurate computed values of vorticity and largest Percentage Relative Error. Contrasted with clustered grid, the uniform Grid 5 has its largest step-size (grid spacing) closest to the boundary, which explains the large Percentage Relative Error associated with it.
Standard, second-order accurate scheme that uses the natural order of grid points produces results illustrated in Table 14 which, consistently, emphasizes the superiority of the (1,2,3) scheme when using Grid 3. The Percentage Relative Error associated with this combination is 0.146%. The four, third-order accurate schemes produce results reported in Table 15, and echo similar conclusions to the superiority of the natural-order scheme and the use of Grid 3.
Table 14 and Table 15 support the following conclusions:
1) The Percentage Relative Error decreases with increasing accuracy of the scheme employed, for both variable and uniform grids.
2) Grids with lowest Percentage Relative Errors for all standard schemes are, respectively: Grid 3, Grid 2, Grid 1, Gird 4, Grid 5.
3) Schemes that employ the natural order of grid points produce smaller Percentage Relative Errors, for all grids employed.
Table 14. Comparison of values of 
4) Using clustered Grid 3 produces the lowest Percentage Relative Error, for all standard schemes used.
5. Generalization of the Schemes to Computational Flow Field Grid Points
Forward-difference schemes that approximate the derivative at a typical grid point (i,j) in the computational flow domain, using up-to 5 grid points, employ the gridlines j, j + 1, j + 2, j + 3, j + 4, shown in Figure 3.
The standard forward-difference uniform and non-uniform schemes that are based on the natural order of grid lines are listed below for the sake of completeness and ease of reference.
(j, j + 1)-Scheme: first order
For non-uniform grid:

For uniform grid:

(j, j + 1, j + 2) Scheme: second order
For non-uniform grid:

For uniform grid:

(j, j + 1, j + 2, j + 3) Scheme: third order
Table 15. Values of 
Figure 3. Grid lines j, j + 1, j + 2, j + 3, j + 4, used in forward-difference schemes.
For non-uniform grid:

For uniform grid:

(j, j + 1, j + 2, j + 3, j + 4) Scheme: fourth order
For non-uniform grid:

where





For uniform grid:
For uniform grid with step size h, coefficients 

and the fourth-order expression for the first derivative takes the form:

6. Conclusions
The main theme of this work has been the development and testing of numerical schemes for the first derivative using uniform and non-uniform grids. The schemes have been applied to the computation of corner vorticity in the case of viscous fluid flow through a two-dimensional curvilinear channel that has been mapped onto a rectangular computational domain using the von Mises transformation.
The following has been accomplished in this work.
1) A fourth-order accurate scheme that uses 5 grid points has been developed and tested.
2) Third-order accurate schemes not previously reported have been developed and tested in this work.
Results have clearly demonstrated that:
1) Non-uniform grids produce more accurate values of corner vorticity than uniform grids.
2) The clustered grid that consistently produced the best approximation to corner vorticity is Grid 3, which is based on a stretching of physical coordinates using the cubic root function. This produced the smallest grid- spacing closest to the boundary in both the physical and computational domains.
3) The schemes that produced the best approximation to corner vorticity are the standard schemes which employ the natural order of grid points.
Acknowledgements
S. O. Alharbi, gratefully acknowledges support for this work through his PhD scholarship from Majmaah University, Kingdom of Saudi Arabia.
Cite this paper
S. O. Alharbi,M. H. Hamdan, (2016) High-Order Finite Difference Schemes for the First Derivative in Von Mises Coordinates. Journal of Applied Mathematics and Physics,04,524-545. doi: 10.4236/jamp.2016.43059
References
- 1. Hamdan, M.H. (1997) Natural Coordinate System Approach to Coupled n-Phase Fluid Flow in Curved Domains. Applied Mathematics and Computation, 85, 297-304.
http://dx.doi.org/10.1016/S0096-3003(96)00144-0 - 2. Fletcher, C.A.J. (1988) Computational Techniques for Fluid Dynamics. Vol. II, Chapter 17, Springer-Verlag.
http://dx.doi.org/10.1007/978-3-642-97071-9 - 3. Gupta, M.M. (1983) A Survey of Some Second-Order Difference Schemes for the Steady State Convection-Diffusion Equation. International Journal for Numerical Methods in Fluids, 3, 319-331.
http://dx.doi.org/10.1002/fld.1650030403 - 4. Kalnay de Rivas, E. (1972) On the Use of Non-Uniform Grids in Finite-Difference Equations. Journal of Computational Physics, 10, 202-210.
http://dx.doi.org/10.1016/0021-9991(72)90060-5 - 5. Barron, R.M. (1989) Computation of Incompressible Potential Flow Using von Mises Coordinates. Mathematics and Computers in Simulation, 31, 177-188.
http://dx.doi.org/10.1016/0378-4754(89)90157-2 - 6. Spotz, W.F. and Carey, G.F. (1998) Formulation and Experiments with High-Order Compact Schemes for Non-Uniform Grids. International Journal of Numerical Methods for Heat & Fluid Flow, 8, 288-303.
http://dx.doi.org/10.1108/09615539810206357 - 7. Veldman, A.E.P. and Rinzema, K. (1992) Playing with Non-Uniform Grids. Journal of Engineering Mathematics, 26, 119-130.
http://dx.doi.org/10.1007/BF00043231 - 8. Agarwal, R.K. (1981) A Third-Order-Accurate Upwind Scheme for Navier-Stokes Solutions in Three Dimensions. In: Computers in Flow Predictions and Fluid Dynamics Experiments, Proceedings of the Winter Annual Meeting, Washington DC, 15-20 November 1981, 73-82.
- 9. Alderson, T.L., Allan, F.M. and Hamdan, M.H. (2007) On the Universality of the von Mises Transformation. International Journal of Applied Mathematics, 20, 109-121.
- 10. Hamdan, M.H. (2009) Recent Developments in the von Mises Transformation and Its Applications in the Computational Sciences: Plenary Lecture. In: Perlovsky, L., et al., Eds., Mathematical Methods, System Theory and Control, MAMECTIS09, 180-189.
- 11. Shukla, R.K., Shukla and Zhong, X. (2005) Derivation of High-Order Compact Finite Difference Schemes for Non-Uniform Grid Using Polynomial Interpolation. Journal of Computational Physics, 204, 404-429.
http://dx.doi.org/10.1016/j.jcp.2004.10.014 - 12. Siyyam, H.I., Ford, R.A. and Hamdan, M.H. (2009) First-Order Accurate Finite Difference Schemes for Boundary Vorticity Approximations in Curvilinear Geometries. Applied Mathematics and Computation, 215, 2378-2387.
http://dx.doi.org/10.1016/j.amc.2009.08.028 - 13. Castillo, J.E., Hyman, J.M., Shashkov, J.M. and Steinberg, S. (1995) The Sensitivity and Accuracy of Fourth Order Finite-Difference Schemes on Non-Uniform Grids in One Dimension. Computers and Mathematics with Applications, 30, 41-55.
http://dx.doi.org/10.1016/0898-1221(95)00136-M - 14. Pandit, S.K., Kalita, J.C. and Dalal, D.C. (2008) A Fourth Order Accurate Compact Scheme for the Solution of Steady Navier-Stokes Equations on Non-Uniform Grids. Computers and Fluids, 37, 121-134.
http://dx.doi.org/10.1016/j.compfluid.2007.04.002 - 15. Visbal, M.R. and Gaitonde, D.V. (2002) On the Use of Higher-Order Finite Difference Schemes on Curvilinear and Deforming Meshes. Journal of Computational Physics, 181, 155-185.
http://dx.doi.org/10.1006/jcph.2002.7117 - 16. Awartani, M.M., Ford, R.A. and Hamdan, M.H. (2005) Computational Complexities and Streamfunction Coordinates. Applied Mathematics and Computation, 169, 758-777.
http://dx.doi.org/10.1016/j.amc.2004.09.088
NOTES
*Corresponding author. On leave from Majmaah University, Kingdom of Saudi Arabia.






