Received 3 November 2015; accepted 14 December 2015; published 17 December 2015

ABSTRACT

A Cauchy problem for the semi-linear elliptic equation is investigated. We use a filtering function method to define a regularization solution for this ill-posed problem. The existence, uniqueness and stability of the regularization solution are proven; a convergence estimate of Hölder type for the regularization method is obtained under the a-priori bound assumption for the exact solution. An iterative scheme is proposed to calculate the regularization solution; some numerical results show that this method works well.

Keywords:

Ill-Posed Problem, Cauchy Problem, Semi-Linear Elliptic Equation, Filtering Function Method, Convergence Estimate

1. Introduction

Let 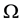be a bounded, connected domain in 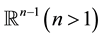with a smooth boundary 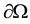and assume that H is a real Hilbert space. We consider the following Cauchy problem of a semi-linear elliptic partial differential equation

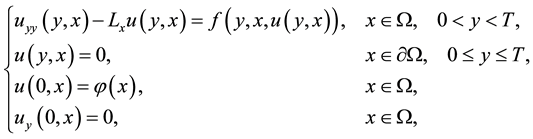(1.1)

where 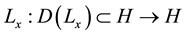denotes a linear densely defined self-adjoint and positive-definite operator with respect to x. The function 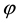is known, and 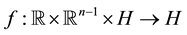is an uniform Lipschitz continuous function, i.e., existing 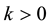independent of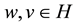, , 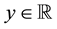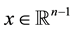such that

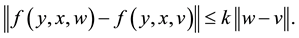(1.2)

Further, we suppose 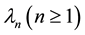be the eigenvalues of the operator, i.e., for the boundary value problem

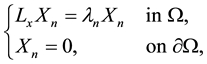(1.3)

there exists a nontrivial solution. And satisfy

(1.4)

Our problem is to determine from problem (1.1).

Problem (1.1) is severely ill-posed, i.e., a small perturbation in the given Cauchy data may result in a dramatic error on the solution [1] . Thus regularization techniques are required to stabilize numerical computations, (see [1] [2] ). We know that, as the right term, it is the Cauchy problem of the homogeneous elliptic equations. For the homogeneous problem, there have many regularization methods to deal with it, (see [3] -[8] ). We note that, these references mainly consider the Cauchy problem of linear homogeneous elliptic operator equation, but the literature which involves the semi-linear cases is quite scarce. In 2014, [9] considered the problem (1.1), where the authors used Fourier truncated method to solve it and derived the convergence estimate of logarithmic type. Recently, there are some similar works about the Cauchy problem for nonlinear elliptic equation, and they have been published, such as [10] [11] .

In the present paper, we adopt a filtering function method to deal with this problem. The idea of this method is similar to the ones in [4] [5] [12] [13] , etc. However, note that our method here is new and different from them in the above references (see Section 2). Meanwhile we will derive the convergence estimate of Hölder type for this method, which is an improvement for the result in [9] .

This paper is organized as follows. In Section 2, we use the filtering function method to treat problem (1.1) and prove some well-posed results (the existence, uniqueness and stability for the regularization solution). In Section 3, a Hölder type convergence estimate for the regularized method is derived under an a-priori bound assumption for the exact solution. Numerical results are shown in Section 4. Some conclusions are given in Section 5.

2. Filtering Function Method and Some Well-Posed Results

2.1. Filtering Function Method

We assume there exists a solution to problem (1.1), then it satisfies the following nonlinear integral equation (see [9] )

(2.1)

here, are the orthonormal eigenfunctions for the operator, and

(2.2)

is the inner product in H.

From (2.1), we can see that the functions, tend to infinity (as),

so in order to guarantee the convergence of solution, the high frequencies() of two functions need to be eliminated. Therefore, a natural way is to use a filter function to filter out the high

frequencies of, and obtain a stable approximate solution, this is so-

called filtering function method.

Let be the noisy data, and satisfying

(2.3)

where is the error level, is the H-norm. According to the above description, for, we choose the

filter function, and define the following regularization solution

(2.4)

where, ,.

In fact, it can be verified that (2.4) satisfies the following mixed boundary value problem formally

(2.5)

Our idea is to approximate the exact solution (2.1) by the regularization solution (2.4), i.e., using the solution of (2.5) to approximate the one of (1.1).

2.2. Some Well-Posed Results

Let, , for the fixed, we define the function

(2.6)

then attain unique maximum at the point, and from, , we have

(2.7)

note that, when, it can be obtained that

(2.8)

Now, we prove that the problem (2.4) is well-posed (existence, uniqueness and stability for the regularization solution), the proof mentality of Theorem 2.1 mainly comes from the references [14] , which describes the ex- istence and uniqueness for the solution of (2.4).

Theorem 2.1. Let, f satisfies (1.2), then the problem (2.4) exists a unique solution .

Proof. For, we consider the operator defined by

(2.9)

then for, , we can prove the following estimate is valid

(2.10)

where, denotes the sup norm in.

For, we firstly use the induction principle to prove

(2.11)

Note that, for, from (2.7),. Meanwhile, use the basic inequalities

, , and. When, from

(2.9), (1.2), we have

When, we suppose

(2.12)

then for, by (2.12), it similarly can be proven that

By the induction principle, we can obtain that

(2.13)

hence, it is clear that

(2.14)

We consider, and from real analysis, we know

(2.15)

There must exist a positive integer number, such that, therefore is a contraction,

it shows that the equation has a unique solution. Noting that

, thus,. By the uniqueness of the fixed point of, we have, so the equation has a unique solution. □

In the following, we give and prove the stability of the regularization solution.

Theorem 2.2 Suppose f satisfies (1.2), and be the solutions of problem (2.4) corresponding to the

measured datum and, respectively, then for, we have

(2.16)

where.

Proof. From (2.4), we have

(2.17)

(2.18)

where,.

By (2.17), (2.18), (2.7), (2.8) and (1.2), we have

Subsequently,

using Gronwall’s inequality [15] , we have

(2.19)

then from the above inequality (2.19), the stability result (2.16) can be obtained. □

3. Convergence Estimate

In this section, under an a-priori bound assumption for the exact solution a convergence estimate of Hölder type for the regularization method is derived. The corresponding result is shown in Theorem 3.1.

Theorem 3.1. Suppose that f satisfies the uniform Lipschitz condition (1.2), and u given by (2.1) is the exact solution of problem (1.1), defined by (2.4) is the regularization solution, the measured data satisfies (2.3). If the exact solution u satisfies

(3.1)

and the regularization parameter is chosen as

(3.2)

then for fixed, we have the following convergence estimate

(3.3)

here, , is given in Theorem 2.2.

Proof. Denote be the solution of problem (2.4) with exact data. We know that

(3.4)

From Theorem 2.2, for, we have

(3.5)

By (2.1), (2.4), (2.7), (2.8), we have

For, we get

(3.6)

use Gronwall’s inequality [15] , it can be obtained that

thus

(3.7)

From (3.2), (3.4), (3.5), (3.7) and (2.3), we can obtain the convergence result (3.3). □

4. Numerical Experiments

In this section, we verify the accuracy and efficiency of our given regularization method by the following numerical example

(4.1)

here we take, , , then and.

It is clear that is an exact solution of problem (4.1), thus

,. We choose the measured

data as, where is an error level, and

(4.2)

Let for, the regularization solution with

can be computed by the following iteration scheme

(4.3)

here, and

(4.4)

(4.5)

For a fixed, in order to make the sensitivity analysis for numerical results, we define the relative root mean square error between the exact and approximate solutions as

(4.6)

We adopt the above given algorithms to compute the regularization solution at with,

for Taking for the numerical results for and at, are shown in Figure 1 and Figure 2, respectively. For, the relative root mean square errors for the various error levels and regularization parameters at are shown in Table 1. In the computational procedure, the regulari- zation parameter is chosen by (3.2), and is computed by (4.2).

From Figure 1 and Figure 2 and Table 1, it can be observed that our regularization method is effective and stable. Meanwhile we note that the smaller is, the better the calculation effect is. Table 1 shows that the numerical results become worse when y approaches to 1, which is a common phenomenon in the computation of ill-posed Cauchy problems for the elliptic equation.

5. Conclusion

We use a filtering function method to solve a Cauchy problem for semi-linear elliptic equation. The results of the well-posedness for the approximation problem are given. Under the a-priori bound assumption, the conver- gence estimate of Hölder type has been derived. Finally, we compute the regularization solution by constructing an iterative scheme. Some numerical results show that this method is stable and feasible.

Acknowledgements

The authors would like to thank the reviewers for their constructive comments and valuable suggestions that improve the quality of our paper. The work described in this paper was supported by the SRF (2014XYZ08, 2015JBK423), NFPBP (2014QZP02) of Beifang University of Nationalities, the SRP of Ningxia Higher School (NGY20140149) and SRP of State Ethnic Affairs Commission of China (14BFZ004).

Cite this paper

HongwuZhang,XiaojuZhang, (2015) Filtering Function Method for the Cauchy Problem of a Semi-Linear Elliptic Equation. Journal of Applied Mathematics and Physics,03,1599-1609. doi: 10.4236/jamp.2015.312184

References

NOTES

^*Corresponding author.