Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60679,5 pages
10.4236/jamp.2015.310154
A New Newton-Type Method with Third-Order for Solving Systems of Nonlinear Equations
Zhongli Liu*, Quanyou Fang
College of Biochemical Engineering, Beijing Union University, Beijing, China
Email: *liuzhongli2@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2015; accepted 25 October 2015; published 28 October 2015
ABSTRACT
In this paper, a new two-step Newton-type method with third-order convergence for solving systems of nonlinear equations is proposed. We construct the new method based on the integral interpolation of Newton’s method. Its cubic convergence and error equation are proved theoretically, and demonstrated numerically. Its application to systems of nonlinear equations and boundary-value problems of nonlinear ODEs are shown as well in the numerical examples.
Keywords:
Newton-Type Method, Systems of Nonlinear Equations, Third-Order Convergence, Integral Interpolation

1. Introduction
We consider a system of nonlinear equations as follows:
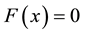 (1)
(1)
where, 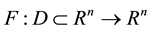 is a given nonlinear function with the following properties:
is a given nonlinear function with the following properties:
1) There exists an 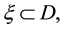 such that
such that ;
;
2)  is continuously differentiable in a neighborhood of
is continuously differentiable in a neighborhood of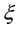 ;
;
3)  is a nonsingular matrix.
is a nonsingular matrix.
How to efficiently solve the system of nonlinear Equation (1) is a typical issue in scientific computation and engineering field. The most famous method is probably Newton’s method as follows (see [1] [2] ):
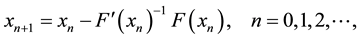 (2)
(2)
where x0 is an initial guess of the root. This is one-step method, and it uses two evaluations of the function and derivative to achieve second-order convergence by iteration.
Besides, third-order iterative equations, such as the Halley iterative method and Chebyshev iterative method, are often used. In recent years, a few similar methods [3] -[9] with high-order have emerged for solving systems of nonlinear equations.
Especially, M. T. Darvish & A. Barati [3] used Adomian decomposition method to construct a third-order Newton-type scheme:
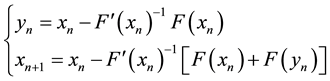 (3)
(3)
Frontini & Sormani [4] presented a third-order method in using numerical quadrature formulae to solve systems of nonlinear equations as follows:
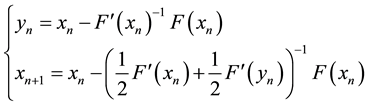 (4)
(4)
These are classic two-step Newton-type methods to achieve cubic convergence to approximate the root of a system of nonlinear equations.
In this paper, we propose a new variant of two-step Newton’s method with the third-order convergence by quadrature formulae in Section 2, some numerical examples using this new method for solving systems of nonlinear equations and boundary-value problems of nonlinear ODEs in Section 3, and finally make conclusions in Section 4.
2. The New Method and Its Third-Order Convergence
Based on the multivariable mean-value theorem
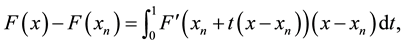 (5)
(5)
we use the left rectangular integral rule

and use 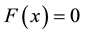 to get Newton Method (1). By using the trapezoidal integral rule
to get Newton Method (1). By using the trapezoidal integral rule
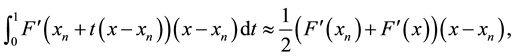
substituting  with
with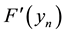 , and using
, and using

Now, we applied the quadrature formula
to construct the following new scheme:

We state and prove the convergence theorem as follows:
Theorem Let 



Proof. As


By Taylor’s expansion, we have
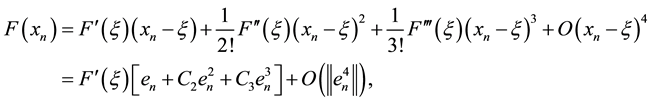

From

where 
We have
By (6), therefore

And
where
By Toylor’s expansion

Furthermore, by (8) and (10), we have

Finally, using (7), (11) and (6), we obtain the error equation as
That is

Using (9), so,

This shows that the method is the third-order convergence.
The new scheme of two-step Newton-type method (6) uses three evaluations of the function and derivative per iteration to achieve third-order convergence for solving a simple root of systems of nonlinear equations. As the efficiency index is


3. Numerical Examples
The iterative method (6) is demonstrated by solving some systems of nonlinear equations and boundary-value problems of nonlinear ODE.
Example 1. Consider the system of nonlinear equation:

where

According to results of the numerical experiments, the new iterative method (6) can achieve super third-order convergence for some systems of nonlinear equations.
Example 2. We have numerical results in Table 2 for the following a system of nonlinear equations:
Table 1. The solutions and errors of the system of Equations (13) using method (6).
Table 2. The solutions of the system of Equations (14) using method (6).
Table 3. The errors of the system of Equations (16) using method (6).
*Corresponding author.
where

The above numerical results agree with the theoretical analysis on the convergence, and the iterative efficiency is comparative high.
Example 3. Consider solving the following boundary-value problem of nonlinear ODE:

Discretize the nonlinear ODE (15) with the finite difference method. Taking nodes



where

The results for the system of nonlinear equations of ODE (15) are shown in Table 3.
4. Conclusion
In this paper, we presented a new two-step iterative method of cubic convergence to solve systems of nonlinear equations. Through theoretical analysis and numerical experiments, we believe that the new variant of Newton- type method is so efficient and fast convergent as to be able to find solutions with required accuracy. To sum up, this method is suitable for solving systems of nonlinear equations, and can be used to resolve boundary-value problems of nonlinear ordinary differential equations as well.
Acknowledgements
The work is funded by the Science & Technology Program of Beijing Municipal Commission of Education (No. KM201511417012).
Cite this paper
ZhongliLiu,QuanyouFang, (2015) A New Newton-Type Method with Third-Order for Solving Systems of Nonlinear Equations. Journal of Applied Mathematics and Physics,03,1256-1261. doi: 10.4236/jamp.2015.310154
References
- 1. Ortega, J.M. and Rheinboldt, W.G. (1970) Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York.
- 2. Traub, J.F. (1964) Iterative Methods for the Solution of Equations. Prentice-Hall, Englewood Cliffs, New Jer-sey.
- 3. Darvish, M.T. and Barati, A. (2007) A Third-Order Newton-Type Method to Solve Systems of Nonlinear Equations. Applied Mathematics and Computation, 187, 630-635.
http://dx.doi.org/10.1016/j.amc.2006.08.080 - 4. Frontini, M. and Sormani, E. (2004) Third-Order Methods from Quadrature Formulae for Solving Systems of Nonlinear Equations. Applied Mathematics and Computation, 149, 771-782.
http://dx.doi.org/10.1016/S0096-3003(03)00178-4 - 5. Weerakoon, S. and Fernando, T.G.I. (2000) A Variant of Newton’s Method with Accelerated Third-Order Convergence. Applied Mathematics Letters, 13, 87-93.
http://dx.doi.org/10.1016/S0893-9659(00)00100-2 - 6. Hafiz, M.A. and Bahgat, M.S.M. (2012) An Efficient Two-Step Iterative Method for Solving System of Nonlinear Equations. Journal of Mathematics Research, 4, 28-34.
- 7. Darvish, M.T. and Barati, A. (2007) A Fourth-Order Method from Quadrature Formulae to Solve Systems of Nonlinear Equations. Applied Mathematics and Computation, 188, 1678-1685.
http://dx.doi.org/10.1016/j.amc.2006.11.022 - 8. Noor, M.A. and Wasteem, M. (2009) Some Iterative Methods for Solving a System of Nonlinear Equations. Computers and Mathematics with Applications, 57, 101-106.
http://dx.doi.org/10.1016/j.camwa.2008.10.067 - 9. Zhang, X. and Tan, J.Q. (2013) The Fifth-Order of Three-Step Iterative Methods for Solving Systems of Nonlinear Equations. Mathematica Numerica Sinica, 35, 297-304.
NOTES
*Corresponding author.








