Received 10 September 2015; accepted 17 January 2016; published 20 January 2016

ABSTRACT

In this paper, we consider a parameterized singularly perturbed second order quasilinear boundary value problem. Asymptotic estimates for the solution and its first and second derivatives have been established. The theoretical estimates have been justified by concrete example.

Keywords:

Parameterized Problem, Asymptotic Bounds, Singular Perturbation, Boundary Layer

1. Introduction

In this paper, we are going to obtain the asymptotic bounds for the following parameterized singularly perturbed boundary value problem (BVP):

(1.1)

(1.2)

where 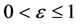is the perturbation parameter, are given constants and 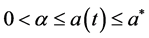is a sufficiently smooth function in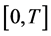. Further, the function is assumed to be sufficiently continuously differentiable for our purpose function in 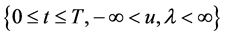and

(1.3)

By a solution of (1.1), (1.2), we mean pair 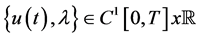for which problem (1.1), (1.2) is satisfied.

An overview of some existence and uniqueness results and applications of parameterized equations may be obtained, for example, in [1] - [10] . In [11] - [14] have also been considered some approxi-mating aspects of this kind of problems. The qualitative analysis of singular perturbation situations has always been far from trivial because of the boundary layer behavior of the solution. In singular perturbation cases, problems depend on a small parameter 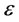in such a way that the solution exhibits a multiscale character, i.e., there are thin transition layers where the solution varies rapidly while away from layers it behaves regularly and varies slowly [15] -[18] . In this note, we establish the boundary layer behaviour for 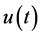of the solution of (1.1)-(1.2) and its first and second derivatives. Example that agrees with the analytical results is given.

2. The Continuous Problem

Lemma 2.1. Let 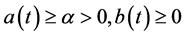and 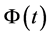be the continuous functions on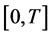. Then, the solution of the boundary-value problem

(2.1)

(2.2)

satisfies the inequality

(2.3)

where

Proof. Under the above conditions, the operatör admits the folloving maximum principle:

Suppose be any function satisfiying , and. Then, for all.

Now, for the barrier fonction

taking also into consideration that, is a solution of the problem

it follows that,

therefore, which immediayely leads to (2.3).

Remark 1. The inequality (2.3) yields.

(2.4)

Theorem 2.1. For and under conditions (1.3), the solution of the problem (1.1), (1.2), satisfies,

(2.5)

(2.6)

where

and

(2.7)

provided and for and.

Proof. We rewrite Equation (1.1) in form

(2.8)

where, intermediate values.

From (2.8) for the first derivate, we have

(2.9)

from which, after using the initial condition, it follows that,

(2.10)

Applying the mean value theorem for integrals, we deduce that,

(2.11)

and

(2.12)

Also, for first and second terms in right side of (2.10) for values, we have

(2.13)

It then follows from (2.11)-(2.13),

(2.14)

Further from (2.4) by taking we get

(2.15)

The inequlities (2.14), (2.15) immediately leads to (2.5), (2.6). After taking into consideration the uniformly boundnees in of and, it then follows from (2.9) that,

which proves (2.7) for. To obtain (2.7) for, first from (1.1) we have

from which after taking into consideration here and (2.5) we obtain

(2.16)

Next, differentiation (1.1) gives

(2.17)

(2.18)

with

and due to our assumptions clearly,

Consequently, from (2.17), (2.18) we have

which proves (2.7) for. □

Example. Consider the following parameterized singular perturbation problem:

with

and selected so that the solution is

where,

First and second derivatives have the form

Therefore, we observe here the accordance in our theoretical results described above.

Cite this paper

MustafaKudu,IlhameAmirali, (2016) A Priori Estimates of Solution of Parametrized Singularly Perturbed Problem. Journal of Applied Mathematics and Physics,04,73-78. doi: 10.4236/jamp.2016.41011

References