Received 29 June 2015; accepted 24 July 2015; published 27 July 2015

ABSTRACT

This paper is concerned with dynamics of the solution to the system of two second-order nonlinear difference equations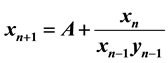, , 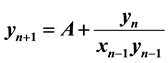, where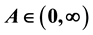, , 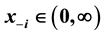, 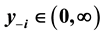i = 0, 1. Moreover, the rate of convergence of a solution that converges to the equilibrium of the system is discussed. Finally, some numerical examples are considered to show the results obtained.

Keywords:

Difference Equation, Boundedness, Stability, Rate of Convergence

1. Introduction

Difference equations or discrete dynamical systems are diverse field which impacts almost every branch of pure and applied mathematics. Every dynamical system 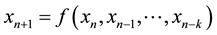determines a difference equation and vise versa. Recently, there has been great interest in studying the system of difference equations. One of the reasons for this is a necessity for some techniques which can be used in investigating equations arising in mathematical models describing real life situations in population biology, economic, probability theory, genetics psychology, etc. The theory of difference equations occupies a central position in applicable analysis. There is no doubt that the theory of difference equations will continue to play an important role in mathematics as a whole. Nonlinear difference equations of order greater than one are of paramount importance in applications. Such equations also appear naturally as discrete analogues and as numerical solutions of differential and delay differential equations. It is very interesting to investigate the behavior of solutions of a system of nonlinear difference equations and to discuss the local asymptotic stability of their equilibrium points. Recently there has been published quite a lot of works concerning the behavior of positive solutions of systems of difference equations [1] -[8] . These results are not only valuable in their own right, but they can provide insight into their differential counterparts.

Papaschinopoulos et al. [1] investigated the global behavior for a system of the following two nonlinear difference equations.

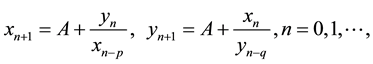
where A is a positive real number; p and q are positive integers, and 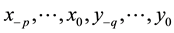are positive real numbers.

Clark and Kulenovic [2] [3] investigated the system of rational difference equations.

where 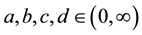and the initial conditions and 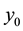are arbitrary nonnegative numbers.

Yang [4] studied the system of high-order difference equations.

where 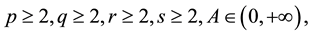and initial values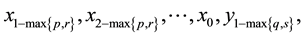 are positive real numbers.

Zhang, Yang and Liu [5] investigated the global behavior for a system of the following third order nonlinear difference equations.

where and initial values

Zhang, Liu and Luo [6] studied dynamical behavior for third-order system of difference equations

where and initial values are positive real numbers.

Ibrahim [7] has obtained the positive solution of the difference equation system in the modeling competitive populations.

Din et al. [8] studied the global behavior of positive solution to the fourth-order rational difference equations

where the parameters and the initial conditions are positive real numbers.

Although difference equations are sometimes very simple in their forms, they are extremely difficult to understand thoroughly the behavior of their solutions. In book [9] , Kocic and Ladas have studied global behavior of nonlinear difference equations of higher order. Similar nonlinear systems of difference equations were investigated (see [10] -[19] ).

Our aim in this paper is to investigate the solutions, stability character and asymptotic behavior of the system of difference equations

(1)

where and initial conditions.

Clearly, if, system (1) has always a positive equilibrium point

2. Boundedness

Theorem 1. Let be a positive solution of (1), then the following statements holds:

1) for each

2) If, then for, we have

(2)

Proof. Assertion 1) is obviously true. Now it only need to prove assertion 2). From (1) and in view of 1), we have, for, that

(3)

Let be the solution of following system, respectively

(4)

such that.

We prove by induction that

(5)

Suppose that (5) is true for From (3) that it follows that

(6)

Therefore (5) is true. From (4) we have

(7)

Then from (3), (5) and (6) the proof of the relation (2) follows immediately.

3. Stability

Theorem 2. Assume that, then the unique positive equilibrium point

is locally asymptotically stable.

Proof. We can obtain easily the linearized system of (1) about the positive equilibrium is

(8)

where

(9)

Let denote the eigenvalues of matrix B, let be a diagonal matrix, where and

Clearly, D is invertible. Computing matrix, we obtain that

From and, it implies that

Furthermore

It is well known that B has the same eigenvalues as, we have that

This implies that the equilibrium of (1) is locally asymptotically stable.

Theorem 3. Assume that. Then every positive solution of (1) converges to.

Proof. Let be an arbitrary positive solution of (1). Let

From Theorem 2, we have This and (1) imply that

which can derive that

(10)

If and, this implies that, which contradict to (10). Therefore we have and, then the and exist. From the uniqueness of the positive equilibrium of (1), we conclude that,.

Combining Theorem 2 and Theorem 3, we obtain the following theorem.

Theorem 4. Assume that. Then the positive equilibrium of (1) is globally asymptotically stable for all positive solutions.

4. Rate of Convergence

In this section we will determine the rate of convergence of a solution that converges to the equilibrium point of the system (1). The following result gives the rate of convergence of solution of a system of difference equations

(11)

where is a four dimensional vector, is a constant matrix, is a matrix function satisfying

(12)

where denotes any matrix norm which is associated with the vector norm.

Theorem 5. [20] Assume that condition (12) hold, if X_n is a solution of (11), then either for all large n or

(13)

or

(14)

exists and is equal to the moduls of one the eigenvalues of the matrix A.

Assume that, we will find a system of limiting equations for the system (1). The error terms are given as

Set, therefore it follows that

where

Now it is clear that

Hence, the limiting system of error terms at can be written as

(15)

where, and

Using Theorem 5, we have the following result.

Theorem 6. Assume that, and be a positive solution of the system (1). Then, the error vector of every solution of (1) satisfies both of the following asymptotic relations

where is equal to the moduls of one the eigenvalues of the Jacobian matrix evaluted at the equilibrium.

5. Numerical Examples

In order to illustrate the results of the previous sections and to support our theoretical discussions, we consider an interesting numerical example in this section.

Example 5.1. Consider the system (1) with initial conditions, Moreover, choosing the parameters. Then system (1) can be written as

(16)

The plot of system (16) is shown in Figure 1.

Example 5.2. Consider the system (1) with initial conditions, Moreover, choosing the parameters. Then system (1) can be written as

(17)

The plot of system (17) is shown in Figure 2.

6. Conclusions and Future Work

In this paper, the dynamical behavior of second-order discrete system is studied. It can be concluded that:

1) The positive equilibrium point is globally asymptotically stable if.

2) The equilibrium rate of convergence is discussed. Some numerical examples are provided to support theoretical results. It is our future work to study the oscillation behavior of system (1).

Acknowledgements

The author would like to thank the Editor and the anonymous referees for their careful reading and constructive suggestions.

Cite this paper

HongmeiBao, (2015) On a System of Second-Order Nonlinear Difference Equations. Journal of Applied Mathematics and Physics,03,903-910. doi: 10.4236/jamp.2015.37110

References