Received 7 April 2015; accepted 11 May 2015; published 14 May 2015

ABSTRACT

This paper considers the asymptotic dynamics of steady states to the Lotka-Volterra competition diffusion systems with random perturbations by two-parameter white noise on the whole real line. By the fundamental solution of heat equation, we get the asymptotic fluctuating behaviors near the stable states respectively. That is, near the steady state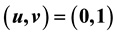, the mean value 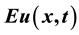is shifted above the equilibrium 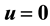and is shifted below the equilibrium. 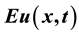How- ever, near the steady state, the mean value is shifted below the equili- brium and.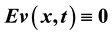

Keywords:

Lotka-Volterra Competition Diffusion System, Random Perturbation, Two-Parameter White Noise

1. Introduction

Nonlinear reaction diffusion systems arise in several fields and have been studied by many authors (see [1] and the references therein). The theory of reaction diffusion waves began in the 1930s with the works by Fisher [2] [3] , Kolmogorov, Petrovsky and Piskunov [4] on propagation of dominant gene and by Zeldovich et al. [5] in population dynamics, mathematical theory of combustion and chemical kinetics [6] . For example, H. C. Tuck- well [7] considered the general nonlinear reaction diffusion equation driven by two-parameter white noise

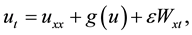(1)

where 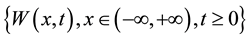was a standard two-parameter Wiener process, i.e., a Gaussian process

with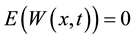, , 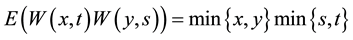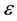was a small real constant, and g was a

function at least twice differentiable at equilibrium.

At present time, it is a well developed area of research which includes qualitative properties of traveling wavefronts for many complex systems. Traveling waves are natural phenomena ubiquitously for reaction diff- usion systems in many scientific areas, such as in biophysics, population genetics, mathematical ecology, chemistry, chemical physics and so on [8] -[14] . It is pretty well understood for a diffusing Lotka-Volterra (LV) system that there exist traveling wavefronts which propagate from an equilibrium to another one [15] .

Consider the LV competition-diffusion system

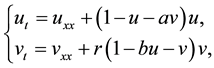(2)

where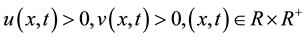, and are positive constants. We look for a monotone travel- ing wave solution of (2), , with wave speed c under the boundary value conditions

(3)

where and are equilibria of (2):

(4)

For or, is a positive equilibrium. By the phase plane technique of

ordinary differential equations in the first quadrant, we have the following cases for the system (see [3] ).

1) Monostable case:

is stable; is unstable,;

is unstable; is stable,.

2) Coexistence case:

is stable,.

3) Bistable case:

and are stable,.

Traveling wavefronts of the system (2) have been studied very extensively. We refer readers to the references for traveling wave solutions connecting two equilibria.

1) Conley and Gardner [16] [17] :

2) Tang and Fife [18] :

3) Kanel and Zhou [19] :

4) Fei and Carr [15] :

For instance, we give some results on the traveling wave solutions of system (2).

Theorem 1. [15] 1) If, for the boundary value problem (2)-(3) with

(5)

there exist positive increasing traveling wavefronts with speed c satisfying .

2) There do not exist traveling wavefront with speed c satisfying

where

Theorem 2. [17] Let and be the velocities of the waves from to and from to, respectively. Then if, there is also a wave from to.

In fact, under the conditions

(6)

X. X. Bao and Z. C. Wang [20] gave explicit traveling wavefronts of the system (2) which connected the equilibria and:

(7)

where.

We know that in a linear system the noise does not affect the mean value at equilibrium; however, in a nonlinear system, the mean is displaced from an equilibrium. How can one describe this displaced mean value? H. C. Tuckwell [7] [21] gave a good idea. Using Green’s functions, he described the nonlinear effects in white noise driven spatial diffusions. Following this idea, E. Z. Wu and Y. B. Tang [22] obtained the asymptotic fluctuating behaviors of the traveling wavefront to the Nagumo equation near two stable steady states.

In this paper, we are interested in calculating the statistical properties of the steady states of the LV competi- tion-diffusion system (2) under the influence of random perturbations by two-parameter white noise on the whole real line

(8)

where is a two-parameter Wiener process such that, formally,

(9)

where stands for a generalized Gaussian random field with zero mean and correlation function

(10)

The initial condition to (8) is with probability one, and is one of the

equilibria (0,1) and (1,0), and the boundary conditions of the traveling wavefront are,

, are positive constants.

We present asymptotic representations of steady states of the LV competition diffusion system that it is randomly perturbed by two-parameter white noise on the whole real line. For a traveling wavefront connecting two stable equilibria and of LV competition diffusion system, we first derive asymptotic representations of solutions near the steady states as. Then by the fundamental solution of heat equation on the whole real line, we get the asymptotic fluctuating behaviors of steady states near the stable states respectively. That is, near the steady state, the mean value is shifted above the equilibrium and is shifted below the equilibrium. However, near the steady state, the mean value is shifted below the equilibrium and is not affected by the noise perturbation.

2. Random Perturbations on a Stationary State

For, under the conditions (6), the system (2) has a monotone traveling wave solution connecting the two stable states and. Let be an equilibrium of (2), i.e., or.

We write the solution of the system (2) as

(11)

and rewrite the system (8) in the following form

(12)

where

(13)

(14)

We put (11) into (12). Equating coefficients of powers of, we get the first two terms of a sequence of linear stochastic partial differential equations (SPDEs)

(15)

(16)

As we know, the fundamental solution of the deterministic linear system

(17)

is

(18)

where is the Green’s function of the heat equation. It is easy to check that

(19)

From the sequence of linear SPDEs we have the solutions of initial value problems (15) and (16), respectively

(20)

(21)

According to the zero-mean property of Itô integral we have

(22)

(23)

These give the expectation of stochastic process to order near the equilibrium

(24)

3. Asymptotic Random Perturbations on the Left Stable State

The equilibrium is the left stable state of the traveling wavefront of (2), i.e.,. Now we consider the equilibrium. Under the condition (6), the linearized matrix of (2) at is

(25)

it has two negative eigenvalues, and there is an invertible matrix

such that

(26)

thus

(27)

Therefore, the solution of (15) is

(28)

(29)

In order to compute the expectations and, we first calculate the following quantities.

(30)

(31)

Since, and

(32)

so we have

(33)

Since, and

(34)

so we have

(35)

Therefore, we get

(36)

that is,

(37)

As complexity of the formula of expectation and, it is very difficult to determine

the signs of and respectively, we just consider the asymptotic behavior of

and as.

By the formula

(38)

and l’Hôpital’s rule, we have

(39)

Denote since

and, then, , therefore

(40)

Similarly, we have

calculating the limits we have

(41)

as in (6), we have

that is,

(42)

where

(43)

since for, hence, then and (42) imply that

(44)

Therefore, we get the random perturbation of the traveling wave solution of (8) near the equilibrium point:

(45)

(46)

(47)

since

these imply that the effect of zero-mean white noise on the system near the lower equilibrium is to increase the expected value of for all x, that is, the mean value is shifted above the equili- brium. Similarly, near the upper equilibrium the white noise is to decrease the expected value of for all x, that is, the mean value is shifted below the equilibrium.

4. Asymptotic Random Perturbations on the Right Stable State

We now consider another equilibrium that is the right stead state of traveling wavefront of (2), i.e.. Now we consider the equilibrium. According to the condition (6), the linearized matrix of (2) at is

(48)

it has two negative eigenvalues, and there is an invertible matrix

such that

(49)

thus

(50)

Therefore, the solution of (15) is

(51)

so we have

(52)

(53)

The solution of (16) is

(54)

hence we have, and

(55)

Let, we have

(56)

Then, we get the random perturbation of the traveling wavefront of (8) near the equilibrium point:

(57)

(58)

(59)

From (56),

implies that the effect of zero-mean white noise on the system near the lower equilibrium is to decrease the expected value of for all x, that is, the mean value is shifted below the equilibrium. On the other hand, and imply that the random perturbations do not alter the mean value near the lower equilibrium for all x, in fact.

Remark 1. In the future paper, we will consider simulation of solutions on bounded domains and compare with the present analytical results. Also, we want to consider the system that the white noise is included in the 2nd component of (8), but according to the complicated calculations in Sections 3 and 4, we must look for a new idea to deal with this coupled problem.

Acknowledgements

This work was supported by National Natural Sciences Foundation of China (Grant No. 11471129). Corresponding author: Yanbin Tang.

References