Journal of Applied Mathematics and Physics
Vol.03 No.03(2015), Article ID:55165,15 pages
10.4236/jamp.2015.33045
Tensor-Product Representation for Switched Linear Systems
Dengyin Jiang, Lisheng Hu
Department of Automation, Shanghai Jiao Tong University, Shanghai, China
Email: lshu@sjtu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 February 2015; accepted 25 March 2015; published 30 March 2015
ABSTRACT
This paper presents the method for the construction of tensor-product representation for multivariate switched linear systems, based on a suitable tensor-product representation of vectors and matrices. We obtain a representation theorem for multivariate switched linear systems. The stability properties of the tensor-product representation are investigated in depth, achieving the important result that any stable switched systems can be constructed into a stable tensor-product representation of finite dimension. It is shown that the tensor-product representation provides a high level framework for describing the dynamic behavior. The interpretation of expressions with- in the tensor-product representation framework leads to enhanced conceptual and physical un- derstanding of switched linear systems dynamic behavior.
Keywords:
Switched Linear Systems, Tensor-Product Representation, Stability

1. Introduction
Switched systems as an important class of hybrid systems [1] have drawn considerable attention in recent years. This is mainly due to the switched and hybrid nature of many physical processes and the growing use of computers in the control of physical plants [2] [3] . And, many dynamical systems encountered in engineering practice exhibit switching between several subsystems that is dependent on various environmental factors, for example, sampled-data control systems [4] -[9] , Markov jump systems [10] -[12] , and references therein. The extensive engineering applications of switched systems are also motivated by the better performance that can be achieved using a controller switching strategy [13] [14] . Currently, there is enormous growth in the literature in the study of switched systems [15] -[17] . These dynamical systems combine behaviors that are typical of continuous-time dynamical systems with behaviors that are typical of discrete-time dynamical systems. Hybrid systems [1] , in which continuous dynamics and discrete events coexist, are considered to be a natural modeling framework for switched systems. Thus, a switched system is a dynamical system that consists of a finite number of subsystems described by differential or difference equations and a logical rule that orchestrates switching between these subsystems [2] [15] [16] [18] -[20] .
On the other hand, switched systems cannot be represented in the framework of linear operators due to the logical switching space. For multivariate systems, the relationship between the rows vectors of the matrix space and that between the column vectors might be important for finding a projection to represent the systems operator. Motivated by this idea, switched systems may be represented in the framework of multi-linear algebra. Multi- linear algebra, the algebra of higher-order tensors, may be applied for analyzing the multi-factor structure of switched systems, including input space and logical switching space. Based on the considerations of multi-linear algebra, tensor-product representation is used to investigate the switched systems expression. From the theoretical point of view, this approach extended the subspace method using matrix technique to the multivariate switch- ed systems. The multilinear algebra, the algebra of higher-order tensors (also being a multidimensional or N- way array), which are the higher-order equivalents of vectors (first order) and matrices (second order), i.e., quan- tities of which the elements are addressed by more than two indices, may be applied for analyzing the multifac- tor structure of multivariate switched systems or such class of nonlinear systems.
In this paper, we investigated the more general problem of tensor-product representations for multivariate switched linear systems. We obtain the tensor-product representation theorem for globally table or globally asymptotically stable multivariate switched linear systems which are only defined on subspaces of algebras. This generalization allows us to obtain a Hahn-Banach extension theorem for such maps, which leads to further results on the Haagerup tensor-product norm applied into more general class of nonlinear systems. The stability properties of the tensor-product representation are investigated in depth, which any stable switched system admits a stable tensor-product representation of finite dimension. It is shown that the tensor-product representation provides a high level framework for describing the dynamic behavior of switched systems. The interpretation of expressions within the tensor-product representation framework leads to enhanced conceptual and physical understanding of switched linear systems dynamic behavior.
The main contribution of this paper is to obtain a general expression of tensor-product representation for multivariate switched systems, and the tensor-product representation is conceptually simple and relatively easy to express on the Haagerup tensor-product norm for multivariate switched systems. We focus on the correspondence between completely bounded multilinear maps and completely bounded linear maps on tensor products endowed with the Haagerup norm [21] -[23] . An abstract characterization of operator systems allows us to embed these tensor product spaces into C*-algebras, after which the techniques developed in [24] lead to the extension and representation theorem. The idea of matrix multiplication spread from the definition of a completely bounded multilinear operator to the Haagerup tensor product and matricial operator spaces has implemented, see [25] [26] for a detailed discussion of completely bounded linear operators, and [22] [27] for the multilinear case. And more details can be founded in related review paper [28] .
The rest of this work is organized as follows. Section 2 contains the preliminaries on the tensor-product of vectors and matrices and the basic algebraic tools are provided. Section 3 gives the problem formulation for multivariate switched linear systems expression and its relation with bilinear algebra expression. In Section 4, the tensor-product representation for multivariate switched linear systems are investigated, and the stability pro- perties of the tensor-product representation based on the proposed methods are also investigated, which is followed by concluding conclusion in Section 5.
Notations: The notations throughout this paper are standard. Rn denotes the n dimensional Euclidean space. Rn×m is the set of all n × m real matrices. G denotes the systems function. I is the identity matrix with appropriate dimensions,
 is the inner product, and
is the inner product, and
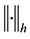 is the Haagerup norm. The symbol
is the Haagerup norm. The symbol
 denotes the direct sum of vectors or spaces, as well as
denotes the direct sum of vectors or spaces, as well as
 and
and
 denote the matching elementwise Kronecker product and Kronecker product, respectively. And, tensors are written as calligraphic letters
denote the matching elementwise Kronecker product and Kronecker product, respectively. And, tensors are written as calligraphic letters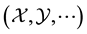 .
.
2. Preliminaries
In this section, we give some necessary preliminaries on the tensor-product of vectors and matrices, mainly concerning with basic algebraic tools on definitions and the correspondence between completely bounded bilinear maps and completely bounded linear maps on Haagerup tensor products norm, which will be used in this paper. And, the C*-algebraic technique is used to investigate the tensor-product representation of multivariate switched linear systems.
Let A and B denote unital C* algebras and E and F will denote subspaces. E* and F* will denote the subspaces consisting of the adjoints of elements in E and F, respectively. The Haagerup norm on the algebraic tensor pro- duct
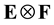 is defined as follows,
is defined as follows,
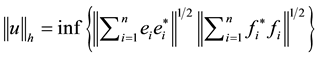 (1)
(1)
where the infimum is taken over all possible representations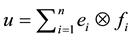 . The resulting normed space is written
. The resulting normed space is written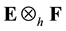 . It is clear from the definitions that
. It is clear from the definitions that
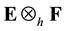 is a matrix normed space in the sense of the re- ference [29] .
is a matrix normed space in the sense of the re- ference [29] .
Let
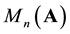 denote the C*-algebra of n × n matrices over the field of complex numbers. If V is a vector space then the space
denote the C*-algebra of n × n matrices over the field of complex numbers. If V is a vector space then the space
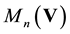 of n × n matrices over V is naturally a vector space; indeed
of n × n matrices over V is naturally a vector space; indeed
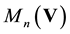 is a bimodule over the ring
is a bimodule over the ring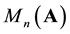 . If
. If
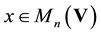 and
and



Definition 1 [30] Let







It is valuable to note that if L is a matrix of scalars, then
If





where the infimum is taken over all such expressions for







Definition 2 [28] Let A and B be C*-algebras, and let









and the completely bounded norm


Proposition 1 [28] Let





Let











It is easiest to visualize this as formal matrix multiplication of




Lemma 1 [22] The Haagerup norm on


Proposition 2 [22] Let




3. Problem Formulation
We consider a collection of discrete-time linear systems described by the equations with parametric uncertainties of process transfer functions and disturbance transfer functions with a class of piecewise constant functions,


where











where

It is assumed that the multivariate switched linear systems is globally table or globally asymptotically stable. This assumption essentially is to guarantee the entire switched systems are completely bounded, which is the very key condition for our study here. For this assumption, an interesting question is: under what conditions it is possible to transform the switched linear system in (6) into descriptive multilinear systems framework and further develop the tensor-product representation theorem. It is also desirable that the tensor-product representation property should promote efficiently numerical computation with respect to the multidimensional time series data analysis for estimating the controller performance of multivariate switched linear systems. The main goal of this paper is to obtain a necessary and sufficient condition for the existence of tensor-product representation for (6) based on such multilinear algebra framework. The problem can be formulated as follows.
Problem 1 Given the switched linear system described in (6), derive necessary and sufficient conditions for tensor-product representation of systems operators, which show that the algebraic structure of switched linear systems can abstractly represented in tensor space.
In order to let the developed results focus on the tensor-product representation framework of multivariate switched linear systems in this paper, we consider the simplified systems description form with neglecting the effects of disturbances at in the following,

Then, we can obtain the switched linear systems operator

where U and Y represent the inputs space and outputs space of subsystems, respectively and the L represents the logical switching space. And the logic switching signals function


where T denotes the logical operators with the same meaning in (7). From the expression (10), we can see that there exists a map from the switched linear systems outputs to the switching signals. Obviously, the expression (9) exactly describes the map of multivariate switched linear systems from bilinear algebra framework. The systems operator description in (8) can be interpreted as dynamical systems behavior in the physical processes, and the equivalent bilinear form in (9) is expressed from the point of view of algebra structure, which is suitable for the technical development of tensor-product representation approach for controller performance measure of multivariate switched linear systems or such more complex class of multivariate nonlinear systems.
4. Tensor-Product Representations
In this section, we discuss the tensor-product representation of multivariate switched linear systems from the point of view of systems operator by employing the theory of multilinear algebra. We first give a representation theorem for complete bounded linear operator on
Theorem 3 [22] If






where
Corollary 1 If






Proof. Combine Proposition 2 with Theorem 3, the result is followed.
Now, we focus on studying the tensor-product representation of completely bounded bilinear operators from A × B into




for all










For a linear operator







Let





in
Lemma 2 Let




Proof. First of all, we define completely bounded maps


For completely bounded operators, from Theorem 3 we can obtain

And more details can be found in Theorem 4. If F and G are completely bounded, we have

where




Lemma 3 If







Proof. By Proposition 2,



If




This map need not be bounded unless both


Consider the simplified form of multivariate switched linear systems described in (9), we give the result of the representation theorem as in the following.
Theorem 4 Consider the multivariate switched systems described in (9), the associated linear map




The linear operators



The proof can be found in the Appendix.
Remark 1 There can be no extension theorem for general bilinear maps. If P

is another completely bounded linear operator from






Suppose that









If we let




Proposition 5 Consider multivariate switched linear systems described in (9) and (10) with the associated linear map:






where
Proof. Applying Theorem 3, the result is followed.
From the expressions (11) in Theorem 3 and (23) in Proposition 5, it is shown that the bilinear systems and switched linear systems are the same with the linear systems representation form. However, from (7) of the switched linear systems description in previous section, it can be found that systems outputs determine the logical switching signals described in (10), which shows the contraction T in Proposition 5 is determined in the operator itself (or switched linear systems itself). Furthermore, the logical functions outputs values are the logical values 0 or 1, so the logical functions outputs values are determined for the entire dynamical systems, of course, for the active subsystem, the logical value is 1. More details will be shown in the proof of Theorem 7.
Theorem 6 [22] Let H be a fixed infinite dimensional separable Hilbert space. The norm in


where the supremum is taken over all complete contractions

Lemma 4 Consider multivariate switched linear systems described in (9) and (10). Let




completely bounded. In this case, we have
Proof. Applying Theorem 6, the result is followed.
A necessary and sufficient conditions for tensor-product representation of multivariate switched linear systems can now be presented, under the assumption that the open or closed-loop switched linear systems is globally stable or globally asymptotically stable.
Theorem 7 Consider multivariate switched linear systems described in (9) and (10), the tensor-product representation







the linear function


the logical function


The proof can be found in the Appendix.
It is noted that the F in Theorem 4 is defined to be taken over all representations for the linear operators, but the F in Theorem 7 is defined to be taken over all representations of the subsystems operators for multivariate switched linear systems. This difference naturally lead to the different tensor-product representations for the general bilinear systems and the multivariate switched linear systems, and the n in Mn can be interpreted as the integer of the all finite switched subsystems of multivariate switched linear systems. More details can be found in the Examples 1 and 2.
Remark 2 Theorem 7 mainly considers the logic switching space, which exactly describes the tensor-product algebra representation for multivariate switched linear systems, which can extend into the scenario of the time- varying disturbance dynamics. And Theorem 4 just considers the tensor-product algebra representation structure for general bilinear systems operators, which can also extend into more general class of multivariate nonlinear systems in Theorem 10 in this paper. In addition, Theorem 4 shows the tensor-product representation structure for general bilinear operator and Theorem 7 shows the tensor-product representation structure for multi- variate switched linear systems in the framework of bilinear algebra. Furthermore, multivariate switched linear systems essentially can be interpreted as the special class of general bilinear operator with logical linear operator substituting the general linear operators.
Next, we give an example (including operator description and unfolding form) of tensor-product representa- tion for multivariate switched linear systems from the perspective of the structured systems models subject to the explicitly bounded disturbance which guarantees the entire systems are completely bounded.
Example 1 Let the k-th subsystem transfer function


For the dynamical systems, the tensor-product representation for the operator systems can be obtained as

where






where










Intuitively, the systems description can be interpreted as considering a linear combination of the linear operators of the original switched linear system that evolves in an asymptotically stable manner in a subspace. The tensor-product representation algebra system evolves in a higher dimensional space to which the original system can be projected under the stability condition of the entire multivariate switched linear systems. From Example 1, we can see that the multivariate switched dynamical systems can be expressed in the form of tensor-product extending the matrix description of multivariate linear systems.
Remark 3 For the entire switched linear systems, the tensor-product representation


Proposition 8 Let



Proof. The proof follows that of Proposition 2.
Theorem 9 [22] Let











The construction of efficient representations to multivariate functions and related operators plays a crucial role in the numerical analysis of higher dimensional problems arising in a wide range of modern applications. We generalize our results in Theorem 4 to the k-linear operators.
Theorem 10 Let





The i-th linear operator Fi is completely bounded with
The proof can be found in the Appendix.
Remark 4 It is difficult to describe the multivariate nonlinear systems in practical industrial applications. The analytic methods developed in [31] [32] for tensor-product approximations to multidimensional integral operators play an important role in the nonlinear control systems performance assessment. For the case of collocation schemes it focuses on the construction of tensor decompositions which are exponentially convergent in the separation rank. Separable approximation of functions and tensors can be derived by using a corresponding separable expansion of the generating function, including a separable approximation of multivariate functions, and the tensor-product approximation of some analytic matrix-valued functions. In practical applications, the general error estimation should mainly consider in the tensor-product approximations for multivariate switched linear systems. In the near future, we will apply analytically-based representation methods, which are efficient for a special class of function-related operators/tensors. The key observation is that there is a natural duality between separable approximation of the multivariate generating function and the tensor-product decomposition of the related multidimensional array which is suitable for geometric quantization for control systems performance assessment.
Corollary 2 A k-linear operator from Ak into




Proof. From the Theorem 9 and Theorem 10, the results is followed.
Next, we extend the multivariate switched linear systems to the case of time varying disturbance scenario. We also assume that disturbance dynamics are piecewise linear time varying. This type of time varying disturbances are reflected as different output trajectories in different subprocess, each subprocess having the same linear time invariant disturbance models. In other words, it is assumed that the disturbance models are the same within each subprocess, and it is required that the switching sequence of disturbance models is also the same within each subprocess. We will give the tensor-product algebraic representation from the point of view of operator theory in the following.
Theorem 11 Consider multivariate switched linear systems described in (9) and (10) with time varying disturbance dynamics, the tensor-product representation














From the Lemma 4 and Theorem 9, the results is followed.
Now, we will give an example of tensor-product representation for multivariate switched linear systems with time-varying disturbance dynamics. The representation results is constructive for practical industrial process systems modeling framework.
Example 2 A possible tensor expression of system (6) can be described for all the K MIMO subsystems in the tensor-product representation form. And, the j-th disturbance transfer function


For the dynamical systems, the tensor-product representation for the operator systems can be obtained as

where















For the entire switched systems, the tensor-product representation for the operator systems is given as

where





















where



5. Conclusion
A new tensor-product representation for describing the dynamic behavior of switched linear systems has been presented. The tensor-product representation makes it easy to see the relationship between abstractly algebraic expressions that propagate spatial quantities from subsystem-to-subsystem. Abstract dynamic equations arising from a hybrid systems analysis, can be reinterpreted as equivalent operator-formulated equations. This algebra expression can model the behavior of the switched linear systems by the use of a tensor-product representation, which shows that the algebraic structure can simplify switched linear systems expression. The proposed technique is well suited for real and complex systems, and is capable of providing the tensor-product representation of the class of stable nonlinear system. Furthermore, the interpretation of expressions within the tensor-product representation framework can be enhanced conceptual and physical understanding of switched linear systems, or more general of multivariate nonlinear systems, dynamic behavior expression.
Cite this paper
Dengyin Jiang, Lisheng Hu,, (2015) Tensor-Product Representation for Switched Linear Systems. Journal of Applied Mathematics and Physics, 03, 322-337. doi: 10.4236/jamp.2015.33045
References
- Goebel, R., Sanfelice, R.G. and Teel, A.R. (2009) Hybrid Dynamical Systems. IEEE Control Systems Magazine, 29, 28-93.
http://dx.doi.org/10.1109/MCS.2008.931718 - Liberzon, D. and Morse, A.S. (1999) Basic Problems in Stability and Design of Switched Systems. IEEE Control Systems Magazine, 19, 59-70.
http://dx.doi.org/10.1109/37.793443 - Decarlo, R.A., Branicky, M.S., Pettersson, S. and Lennartson, B. (2000) Perspectives and Results on the Stability and Stabilization of Hybrid Systems. Proceedings of the IEEE, 88, 1069-1082.
http://dx.doi.org/10.1109/5.871309 - Hu, L.S., Cao, Y.Y. and Shao, H.H. (2002) Constrained Robust Sampled-Data Control for Nonlinear Uncertain Systems. International Journal of Robust and Nonlinear Control, 12, 447-464.
http://dx.doi.org/10.1002/rnc.632 - Hu, L.S., Lam, J., Cao, Y.Y. and Shao, H.H. (2003) LMI Approach to Robust H2 Sampled-Data Control for Linear Uncertain Systems. IEEE Transactions on Systems Man and Cybernetics Part B, 33, 149-155.
http://dx.doi.org/10.1109/TSMCB.2003.808181 - Hu, L.S., Shi, P. and Huang, B. (2005) H∞ Control for Sampled-Data Linear Systems with Two Markovian Processes. Optimal Control Applications & Methods, 26, 291-306.
http://dx.doi.org/10.1002/oca.761 - Hu, L.S., Shi, P. and Frank, P.M. (2006) Robust Sampled-Data Control for Markovian Jump Linear Systems. Automatica, 42, 2025-2030.
http://dx.doi.org/10.1016/j.automatica.2006.05.029 - Hu, L.S., Bai, T., Shi, P. and Wu, Z.M. (2007) Sampled Data Control of Networked Linear Control Systems. Automatica, 43, 903-911.
http://dx.doi.org/10.1016/j.automatica.2006.11.015 - Shi, P. (1998) Filtering on Sampled-Data Systems with Parametric Uncertainty. IEEE Transactions on Automatic Control, 43, 1022-1027.
http://dx.doi.org/10.1109/9.701119 - Hu, L.S., Shi, P. and Huang, B. (2006) Stochastic Stability and Robust Control for Sampled-Data Systems with Markovian Jump Parameters. Journal of Mathematical Analysis and Applications, 313, 504-517.
http://dx.doi.org/10.1016/j.jmaa.2005.08.019 - Shi, P., Boukas, E.K. and Agarwal, R.K. (1999) Control of Markovian Jump Discrete-Time Systems with Norm Bounded Uncertainty and Unknown Delay. IEEE Transactions on Automatic Control, 44, 2139-2144.
http://dx.doi.org/10.1109/9.802932 - Shi, P., Xia, Y., Liu, G.P. and Rees, D. (2006) On Designing of Sliding-Mode Control for Stochastic Jump Systems. IEEE Transactions on Automatic Control, 51, 97-103.
http://dx.doi.org/10.1109/TAC.2005.861716 - Skafidas, E., Evans, R.J., Savkin, A.V. and Petersen, I.R. (1999) Stability Results for Switched Controller Systems. Automatica, 35, 553-564.
http://dx.doi.org/10.1016/S0005-1098(98)00167-8 - Narendra, K.S., Driollet, O.A., Feiler, M. and George, K. (2003) Adaptive Control Using Multiple Models, Switching and Tuning. International Journal of Adaptive Control and Signal Processing, 17, 87-102.
http://dx.doi.org/10.1002/acs.740 - Lin, H. and Antsaklis, P.J. (2007) Switching Stabilizability for Continuous-Time Uncertain Switched Linear Systems. IEEE Transactions on Automatic Control, 52, 633-646.
http://dx.doi.org/10.1109/TAC.2007.894515 - Lin, H. and Antsaklis, P.J. (2009) Stability and Stabilizability of Switched Linear Systems: A Survey of Recent Results. IEEE Transactions on Automatic Control, 54, 308-322.
http://dx.doi.org/10.1109/TAC.2008.2012009 - Sun, Z. and Ge, S.S. (2005) Analysis and Synthesis of Switched Linear Control Systems. Automatica, 41, 181-195.
http://dx.doi.org/10.1016/j.automatica.2004.09.015 - Zhai, G., Lin, H. and Antsaklis, P. (2003) Quadratic Stabilizability of Switched Linear Systems with Polytopic Uncertainties. International Journal of Control, 76, 747-753.
http://dx.doi.org/10.1080/0020717031000114968 - Athans, M. (1987) Command and Control (C2) Theory: A Challenge to Control Science. IEEE Transactions on Automatic Control, 32, 286-293.
http://dx.doi.org/10.1109/TAC.1987.1104607 - Zhao, X., Zhang, L., Shi, P. and Liu, M. (2012) Stability of Switched Positive Linear Systems with Average Dwell Time Switching. Automatica, 48, 1132-1137.
http://dx.doi.org/10.1016/j.automatica.2012.03.008 - Effros, E.G. and Ruan, Z.J. (1988) Representations of Operator Bimodules and Their Applications. Journal of Operator Theory, 19, 137-157.
- Paulsen, V.I. and Smith, R.R. (1987) Multilinear Maps and Tensor Norms on Operator Systems. Journal of Functional Analysis, 73, 258-276.
http://dx.doi.org/10.1016/0022-1236(87)90068-1 - Ruan, Z.J. (1988) Subspaces of C*-Algebras. Journal of Functional Analysis, 76, 217-230.
http://dx.doi.org/10.1016/0022-1236(88)90057-2 - Paulsen, V.I. (1984) Every Completely Polynomially Bounded Operator Is Similar to a Contraction. Journal of Functional Analysis, 55, 1-17.
http://dx.doi.org/10.1016/0022-1236(84)90014-4 - Effros, E.G. and Ruan, Z.J. (1988) On Matricially Normed Spaces. Pacific Journal of Mathematics, 132, 243-264.
http://dx.doi.org/10.2140/pjm.1988.132.243 - Paulsen, V.I. (1986) Completely Bounded Maps and Dilations. Pitman Research Notes in Mathematics, Longman, London.
- Christensen, E. and Sinclair, A.M. (1987) Representations of Completely Bounded Multilinear Operators. Journal of Functional Analysis, 72, 151-181.
http://dx.doi.org/10.1016/0022-1236(87)90084-X - Christensen, E. and Sinclair, A.M. (1989) A Survey of Completely Bounded Operators. Bulletin London Mathematical Society, 21, 417-448.
http://dx.doi.org/10.1112/blms/21.5.417 - Choi, M.D. and Effros, E.G. (1977) Injectivity and Operator Spaces. Journal of Functional Analysis, 24, 159-209.
http://dx.doi.org/10.1016/0022-1236(77)90052-0 - Tyrtyshnikov, E. (2004) Kronecker-Product Approximations for Some Function-Related Matrices. Linear Algebra and Its Applications, 379, 423-437.
http://dx.doi.org/10.1016/j.laa.2003.08.013 - Hackbusch, W. and Khoromskij, B.N. (2007) Tensor-Product Approximation to Operators and Functions in High Dimensions. Journal of Complexity, 23, 697-714.
http://dx.doi.org/10.1016/j.jco.2007.03.007
Appendix
A.1. Proof of Theorem 4
Proof. The necessity and sufficiency proofs are in the following.
Necessity of proof: Let







for

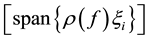 and
and
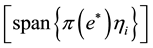 . Then
. Then

Note that if X is any unitary matrix in Mn, then

Such elements are annihilated by

for all unitaries X. This forces the matrix




The element

and


space H and norm one operators




With these definitions it is easy to check that

where





Sufficiency of proof: It follows, from Lemma 2, that







Since
sentations





for

The element

and


space H and norm one operators




Since

It follows that f and g are well-defined and we have

This shows that
A.2. Proof of Theorem 7
Proof. To avoid technical complications, we only discuss the case n = 2. In the other words, consider the multivariate switched linear systems with only two subsystems. The calculations are in the same spirit for general

Necessity of proof: Let










for all







are logical functional gi on H1 such that

Let



for all

for all









Sufficiency of proof: It follows, from Lemma 4, that the







Since










for all

Since very element


for some



for all
And very element


for some



for all

where



lead to

for all

where
Since








A.3. Proof of Theorem 10
Proof. We first consider the case













Since the inclusion





From Lemma 2, we can obtain
combining with inclusion

expression into the formula for









