Journal of Applied Mathematics and Physics Vol.02 No.13(2014),
Article ID:52512,11 pages
10.4236/jamp.2014.213137
A Generalization of Ince’s Equation
Ridha Moussa
University of Wisconsin, Waukesha, USA
Email: rmoussa@uwm.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 October 2014; revised 10 November 2014; accepted 17 November 2014
ABSTRACT
We investigate the Hill differential equation
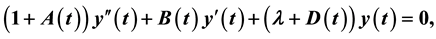 where
where
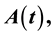
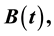 and
and
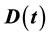 are trigonometric polynomials. We are interested in solutions that are even or odd,
and have period
are trigonometric polynomials. We are interested in solutions that are even or odd,
and have period
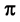 or semi-period
or semi-period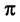 . The above
equation with one of the above conditions constitutes a regular Sturm-Liouville
eigenvalue problem. We investigate the representation of the four Sturm-Liouville
operators by infinite banded matrices.
. The above
equation with one of the above conditions constitutes a regular Sturm-Liouville
eigenvalue problem. We investigate the representation of the four Sturm-Liouville
operators by infinite banded matrices.
Keywords:
Hill Equation, Ince Equation, Sturm-Liouville Problem, Infinite Banded Matrix, Eigenvalues, Eigenfunctions

1. Introduction
The first known appearance of the Ince equation,
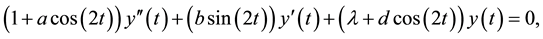
is in Whittaker’s paper ( [1] , Equation (5)) on integral equations. Whittaker emphasized
the special case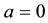 ,
and this special case was later investigated in more detail by Ince [2] [3] . Magnus
and Winkler’s book [4] contains a chapter dealing with the coexistence problem for
the Ince equation. Also Arscott [5] has a chapter on the Ince equation with
,
and this special case was later investigated in more detail by Ince [2] [3] . Magnus
and Winkler’s book [4] contains a chapter dealing with the coexistence problem for
the Ince equation. Also Arscott [5] has a chapter on the Ince equation with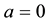 .
.
One of the important features of the Ince equation is that the corresponding Ince differential operator when applied to Fourier series can be represented by an infinite tridiagonal matrix. It is this part of the theory that makes the Ince equation particularly interesting. For instance, the coexistence problem which has no simple solution for the general Hill equation has a complete solution for the Ince equation (see [6] ).
When studying the Ince equation, it became apparent that many of its properties carry over to a more general class of equations “the generalized Ince equation”. These linear second order differential equations describe important physical phenomena which exhibit a pronounced oscillatory character; behavior of pendulum-like systems, vibrations, resonances and wave propagation are all phenomena of this type in classical mechanics, (see for example [7] ), while the same is true for the typical behavior of quantum particles (Schrödinger’s equa- tion with periodic potential [8] ).
2. The Differential Equation
We consider the Hill differential equation
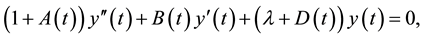 (2.1)
(2.1)
where
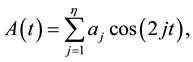
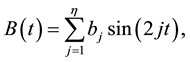
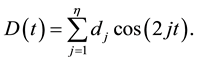
Here
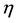 is a positive integer, the coefficients
is a positive integer, the coefficients
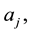



The real number








The polynomials

will play an important role in the analysis of (2.1). For ease of notation we also introduce the polynomials

Equation (2.1) is a natural generalization to the original Ince equation

Ince’s equation by itself includes some important particular cases, if we choose
for example



with associated pzlynomial

If we choose






with associated polynomial

Equation (2.1) can be brought to algebraic form by applying the transformation




3. Eigenvalues
Equation (2.1) is an even Hill equation with period






Lemma 3.1. Let













Equation (2.1) can be written in the self adjoint form

where

Note that




Proof. Let


which is equivalent to

Noting that
and
we see that
Therefore, (3.8) can be written as

Since

In the case of Ince’s Equation (2.4), we have the following formula for the function

When




Equation (2.1) with one of the boundary conditions in lemma 3.1 is a regular Sturm-Liouville
problem. From the theory of Sturm-Liouville ordinary differential equations it is
known that such an eigenvalue problem has a sequence of eigenvalues that converge
to infinity. These eigen values are denoted by





Theorem 3.2. The generalized Ince equation admits a nontrivial even solution with
period








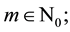


Example 3.3. To gain some understanding about the notation we consider the almost trivial completely solvable example, the so called Cauchy boundary value problem

subject to the boundary conditions of lemma 3.1. We have the following for the eigenvalues


1) Even with period

2) Even with semi-period

3) Odd with semi-period

4) Odd with semi-period


The formal adjoint of the generalized Ince equation is

By introducing the functions
we note that the adjoint of (2.1) has the same form and can be written in the following form:

Lemma 3.4. If




Proof. We Know that
and
For ease of notation, let
then
Substituting for

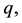



From lemma 3.4 we know that if











Theorem 3.5. We have for


From Sturm-Liouville theory we obtain the following statement on the distribution of eigenvalues.
Theorem 3.6. The eigenvalues of the generalized Ince equation satisfy the inequalities

The theory of Hill equation [4] gives the following results.
Theorem 3.7. If







for some positive integer





4. Eigenfunctions
By theorem 3.2, the generalized Ince’s equation with



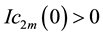

The generalized Ince’s equation with





The generalized Ince equation with





The generalized Ince equation with





From Sturm-Liouville theory ( [11] Chapter 8, Theorem 2.1) we obtain the following oscillation properties.
Theorem 4.1. Each of the function systems




is orthogonal over






Moreover, each of the previous system is complete over
Using the transformations that led to Theorem 3.5, we obtain the following result.
Theorem 4.2. We have


where



with
The adopted normalization of Ince functions is easily expressible in terms of the
Fourier coefficients of Ince functions and so is well suited for numerical computations
[6] ; However, it has the disadvantage that Equations (4.13) and (4.14) require
coefficients


Of course, once the generalized Ince functions






If we square both sides of (4.13) and (4.14) and integrate, we find that


If



Once we know




The integrals on the right-hand sides of (4.19) and (4.20) are easy to calculate once we know the Fourier series of Ince functions.
5. Operators and Banded Matrices
In this section we introduce four linear operators associated with Equation (2.1),
and represent them by banded matrices of width

Let




By restricting functions to




We consider the differential operator

The domain














on the same domain








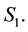



defines a bijective linear map



Let








where












Now consider the operator









defines a bijective linear map


Let



where
Now consider the operator








defines a bijective linear map


Let



where
and
Finally, consider the operator








defines a bijective linear map

Let




where
Example 5.1. For the Whittaker-Hill Equation (2.7) in the following form [8]

the function











6. Fourier Series
The generalized Ince functions admit the following Fourier series expansions




We did not indicate the dependence of the Fourier coefficients on






Using relations (4.13) and (4.14), we can represent the generalized functions in a different way


where
Therefore, we can write




where
and the Fourier coefficients

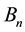




A generalized Ince function is called a generalized Ince polynomial of the first
kind if its Fourier series (6.1), (6.2), (6.3), or (6.4) terminate. It is called
a generalized Ince polynomial of the second kind if its expansion (6.11), (6.12),
(6.13), or (6.14) terminate. If they exist, these generalized Ince polynomials and
their corresponding eigenvalues can be computed from the finite subsections of the
matrices


Example 6.1. Consider the equation

one can check that if we set





References
- Whittaker, E.T. (1915) On a Class of Differential Equations Whose Solutions Satisfy Integral Equations. Proceedings of the Edinburgh Mathematical Society, 33, 14-33. http://dx.doi.org/10.1017/S0013091500002297
- Ince, E.L. (1923) A Linear Differential Equation with Periodic Coefficients. Proceedings of the London Mathematical Society, 23, 800-842.
- Ince, E.L. (1925) The Real Zeros of Solutions of a Linear Differential Equation with Periodic Coefficients. Proceedings of the London Mathematical Society, 25, 53-58.
- Magnus, W. and Winkler, S. (1966) Hill’s Equation. John Wiley & Sons, New York.
- Arscott, F.M. (1964) Periodic Differential Equations. Pergamon Press, New York.
- Volkmer, H. (2003) Coexistence of Periodic Solutions of Ince’s Equation. Analysis, 23, 97-105. http://dx.doi.org/10.1524/anly.2003.23.1.97
- Recktenwald, G. and Rand, R. (2005) Coexistence Phenomenon in Autoparametric Excitation of Two Degree of Freedom Systems. International Journal of Non-Linear Mechanics, 40, 1160-1170. http://dx.doi.org/10.1016/j.ijnonlinmec.2005.05.001
- Hemerey, A.D. and Veselov, A.P. (2009) Whittaker-Hill Equation and Semifinite Gap Schrödinger Operators. 1-10. arXiv:0906.1697v2
- Eastham, M. (1973) The Spectral Theory of Periodic Differential Equations. Scottish Academic Press, Edinburgh, London.
- Volkmer, H. (2004) Four Remarks on Eigenvalues of Lamé’s Equation. Analysis and Applications, 2, 161-175. http://dx.doi.org/10.1142/S0219530504000023
- Coddington, E. and Levinson, N. (1955) Theory of Ordinary Differential Equations. Robert E. Krieger Publishing Company, Malarbar.
- Kato, T. (1980) Perturbation Theory for Linear Operators. Springer-Verlag, Berlin, Heidelberg, New York.













































