Journal of Applied Mathematics and Physics
Vol.2 No.3(2014), Article ID:43178,5 pages DOI:10.4236/jamp.2014.23005
Application of Trial Equation Method for Solving the Benjamin Ono Equation
Yang Li
Department of Mathematics, Northeast Petroleum University, Daqing, China
Email: liyang120918@163.com
Copyright © 2014 Yang Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Yang Li. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received January 7, 2014; revised February 7, 2014; accepted February 15, 2014
ABSTRACT
In the article, the nonlinear equation is reduced to an ordinary differential equation under the travelling wave transformation. Using trial equation method, the ODE is reduced to the elementary integral form. In the end, complete discrimination system for polynomial is used to solve the corresponding integrals and obtain the classification of all single travelling wave solutions to the equation.
Keywords: The Nonlinear Partial Differential Equation; Complete Discrimination System for Polynomial; Trial Equation Method; Traveling Wave Transform; The Benjamin Ono Equation
1. Introduction
Nonlinear phenomena are general problems in every field of engineering technology, science research, natural world and human society activities. So the investigation of exact solutions of nonlinear equations plays a important role not only in theoretic research but in application. To obtain the travelling wave solutions, many methods were attempted, such as the inverse scattering method [1], Hirotas bilinear transformation [2,3], the tanh method [4], sine-cosine method [5], homogeneous balance method [6,7], exp-function method [8], and so on. These methods derived many solutions to most nonlinear evolution equations. Recently, Professor Liu proposed a powerful method named trial equation method for finding exact solutions to nonlinear differential equations [9-11]. By using his method, the nonlinear differential equation is reduced to an ordinary differential equation under the travelling wave transformation. Using the trial equation method, the ODE is reduced to the elementary integral form. In the end, the complete discrimination system for polynomial is used to solve the corresponding integrals. We can obtain the classification of all single travelling wave solutions [12-16] to the equation. This idea is so good that many types of nonlinear differential equations can be solved by it. Using the trial equation method and complete discrimination system for polynomial, we have obtained a lot of new solutions to many nonlinear differential equations. As an application, some new solutions to the Benjamin Ono equation are given.
2. Application of the Trial Equation Method
The Benjamin Ono equation reads as
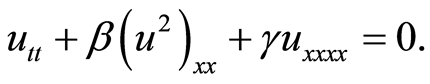 (1)
(1)
where 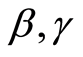 are parameters.Taking the traveling wave transformation
are parameters.Taking the traveling wave transformation 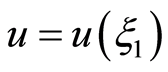 and
and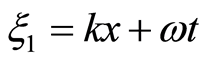 , we can obtain the corresponding reduced ODE.
, we can obtain the corresponding reduced ODE.
 (2)
(2)
we take the trial equation as follows: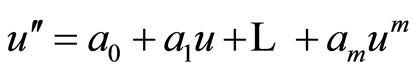 .
.
According to the trial equation method of rank homogeneous equation, balancing 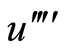 with
with 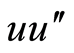 (or
(or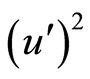 ) gets
) gets . Equation (4) has the following specific form
. Equation (4) has the following specific form
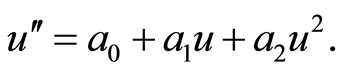 (3)
(3)
Integrating the Equation (3)once with respect to , we get
, we get
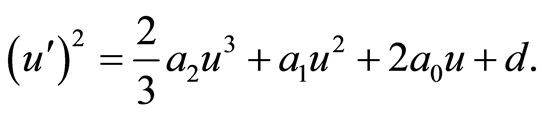 (4)
(4)
By Equation (3) and Equation(4), we derive the following equation
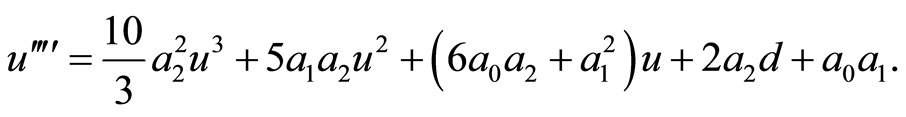 (5)
(5)
Substituting Equations (3)-(5) into Equation (2), we have
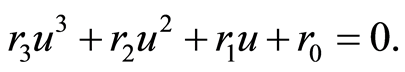 (6)
(6)
where
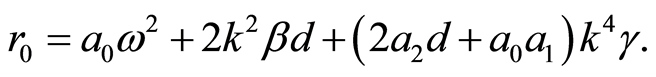 (7)
(7)
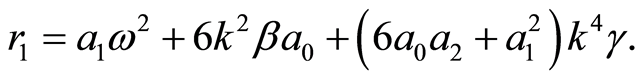 (8)
(8)
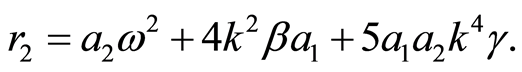 (9)
(9)
 (10)
(10)
Let the coefficient 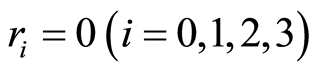 be zero,we will yield nonlinear algebraic equations.Solving the equations, we will determine the values of
be zero,we will yield nonlinear algebraic equations.Solving the equations, we will determine the values of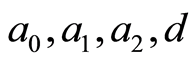 .
.
We get 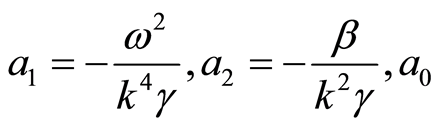 and d are two arbitrary constants. When the above conditions are satisfied, we use the complete discrimination system for the third order polynomial and have the following solving process.
and d are two arbitrary constants. When the above conditions are satisfied, we use the complete discrimination system for the third order polynomial and have the following solving process.
Let
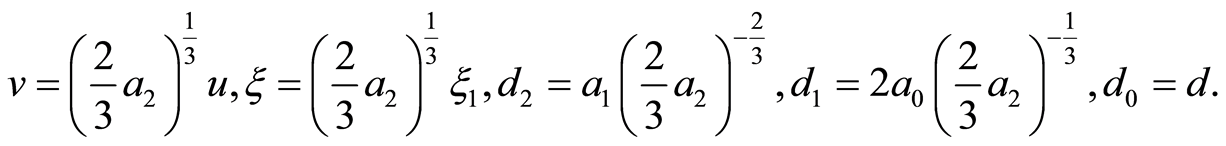 (11)
(11)
Then Equation(4) becomes
 (12)
(12)
where 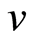 is a function of
is a function of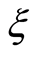 .The integral form of Equation(12) is
.The integral form of Equation(12) is
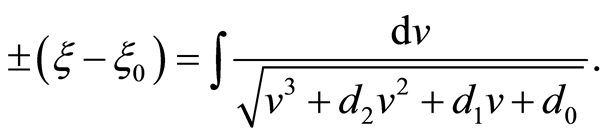 (13)
(13)
Denote
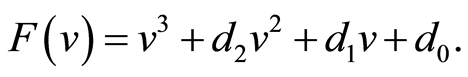 (14)
(14)
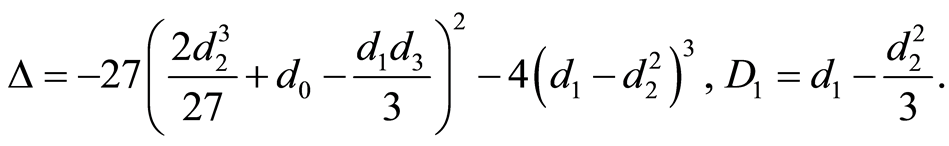 (15)
(15)
According to the complete discrimination system, we give the corresponding single traveling wave solutions to Equation(1).
Case 1.  has a double real root and a simple real root. Then we have
has a double real root and a simple real root. Then we have
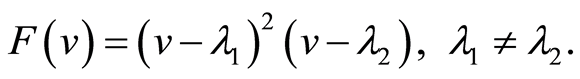 (16)
(16)
when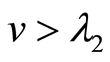 , the corresponding solutions are
, the corresponding solutions are
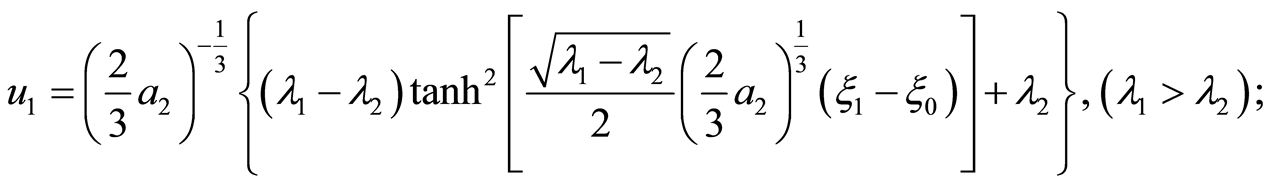 (17)
(17)
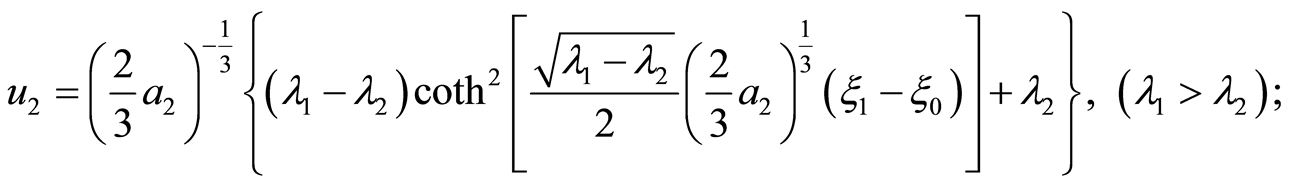 (18)
(18)
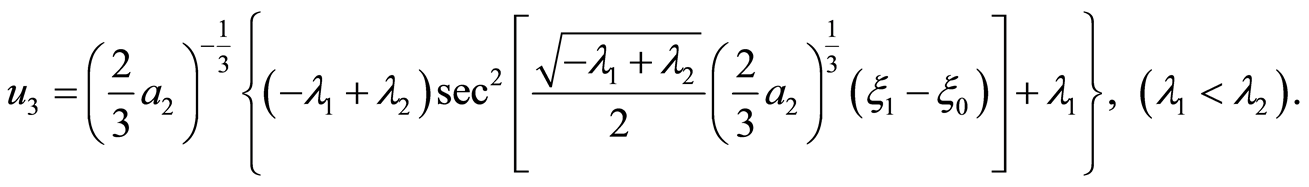 (19)
(19)
Case 2. 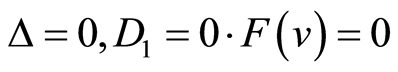 has a triple root. Then we have
has a triple root. Then we have
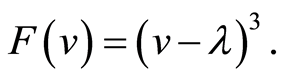 (20)
(20)
The corresponding solution is
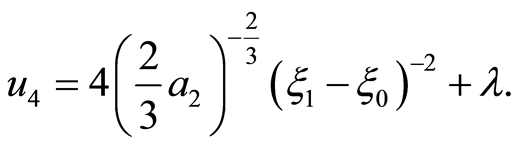 (21)
(21)
Case 3. 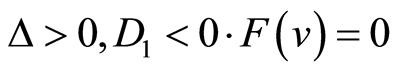 has three different real roots. Then we have
has three different real roots. Then we have
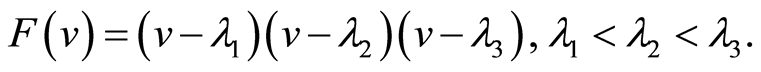 (22)
(22)
when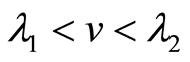 , we take the transformation as follows
, we take the transformation as follows
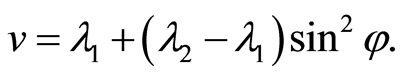 (23)
(23)
According to the Equation(12), we have
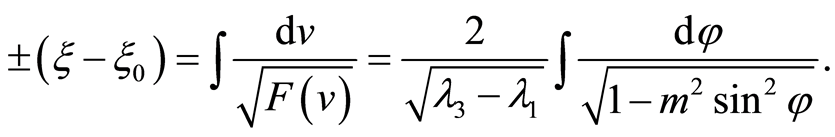 (24)
(24)
where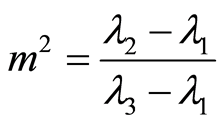 .On the basis of the Equation(24) and the definition of the Jacobi elliptic sine function, we have
.On the basis of the Equation(24) and the definition of the Jacobi elliptic sine function, we have
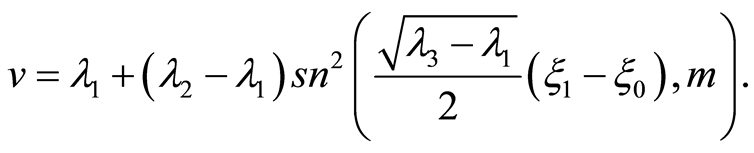 (25)
(25)
The corresponding solutions is
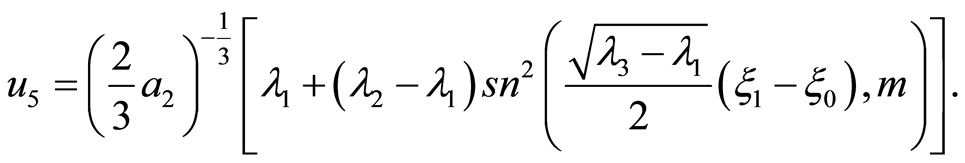 (26)
(26)
when , we take the transformation as follows
, we take the transformation as follows
 (27)
(27)
The corresponding solutions is
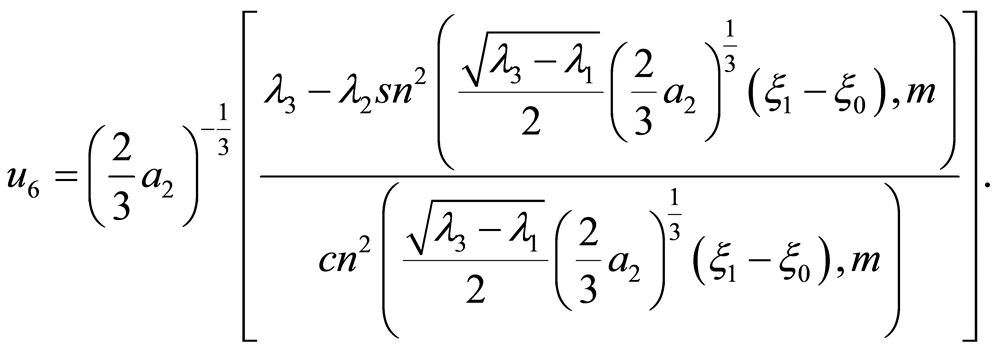 (28)
(28)
where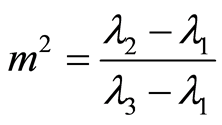 .
.
Case 4. 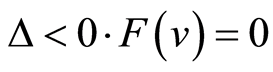 has only a real root. Then we have
has only a real root. Then we have
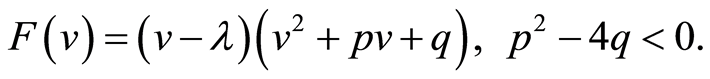 (29)
(29)
when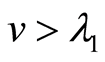 , we take the transformation as follows
, we take the transformation as follows
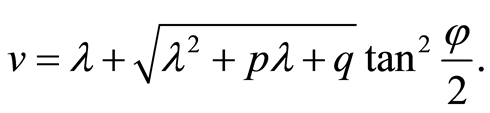 (30)
(30)
According to the Equation(13), we have
 (31)
(31)
where . On the basis of the Equation(31) and the definition of the Jacobi elliptic cosine function, we have
. On the basis of the Equation(31) and the definition of the Jacobi elliptic cosine function, we have
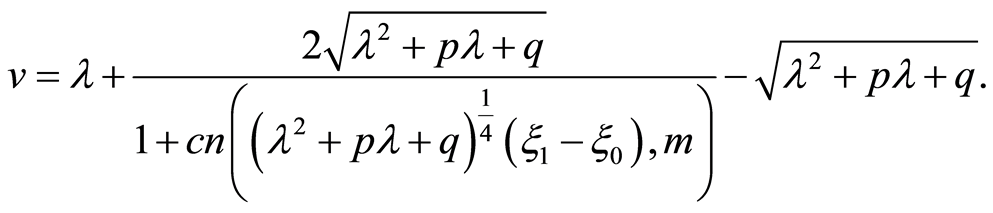 (32)
(32)
The corresponding solutions is
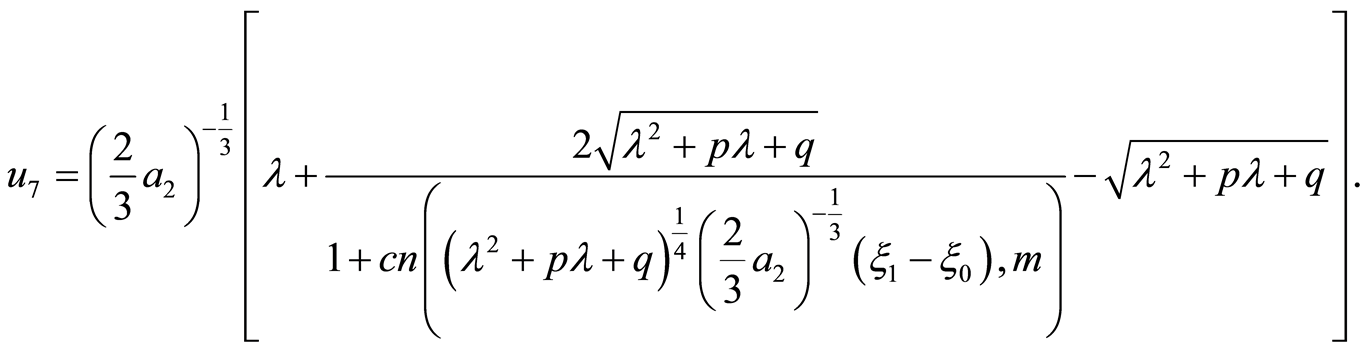 (33)
(33)
In Equations (17), (18), (19), (21), (26), (28) and (33), the integration constant 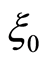 has been rewritten,but we still use it. The solutions
has been rewritten,but we still use it. The solutions  are all possible exact traveling wave solutions to Equation (1). It is easy to write the corresponding solutions to the Benjamin Ono equation. For brevity, we omitted.
are all possible exact traveling wave solutions to Equation (1). It is easy to write the corresponding solutions to the Benjamin Ono equation. For brevity, we omitted.
3. Conclusion
Trial equation method is a systematic method to solve nonlinear differential equations. The advantage of this method is that we can deal with nonlinear equations with linear methods. This method has the characteristics of simple steps and clear effectivity. Based on the idea of the trial equation method and the aid of the computerized symbolic computation, some exact traveling wave solutions to the Benjamin Ono equation have been obtained. With the same method, some of other equations can be dealt with.
Acknowledgements
I would like to thank the referees for their valuable suggestions.
REFERENCES
[1] M. J. Ablowitz and P. A. Clarkson, “Solitous, Non-Linear Evolution Equations and Inverse Scattering,” Cambridge University Press, Cambridge, 1991.
[2] R. Hirota, “Exact Envelope-Soliton Solutions of a Nonlinear Wave Equation,” Journal of Mathematical Physics, Vol. 14, 1973, p. 805. http://dx.doi.org/10.1063/1.1666399
[3] R. Hirota and J. Satsuma, “Soliton Solutions of a Coupled Korteweg-de Vries Equation,” Physics Letters A, Vol. 85, No. 8-9, 1981, p. 407-408. http://dx.doi.org/10.1016/0375-9601(81)90423-0
[4] E. Fan, “Extended Tank-Function Method and Its Applications to Nonlinear Equations,” Physics Letters A, Vol. 277, No. 4, 2000, pp. 212-218.
[5] C. T. Yan, “A Simple Transformation for Nonlinear Waves,” Physics Letters A, Vol. 224, No. 1-4, 1996, pp. 77-84. http://dx.doi.org/10.1016/S0375-9601(96)00770-0
[6] M. Wang, Y. Zhou and Z. Li, “Application of a Homogeneous Balance Method to Exact Solutions of Nonlinearequations in Mathematical Physics,” Physics Letters A, Vol. 216, No. 1, 1996, pp. 67-75.
[7] M. L. Wang, “Solitary Wave Solutions for Variant Boussinesq Equations,” Physics Letters A, Vol. 199, No. 3-4, 1995, pp. 169-172. http://dx.doi.org/10.1016/0375-9601(95)00092-H
[8] W. X. Ma and J. H. Lee, “A Transformed Rational Function Method and Exact Solutions to the 3 + 1 Dimensional Jimbo-Miwa Equation,” Chaos, Solitons and Fractals, Vol. 42, No. 3, pp. 1356-1363. http://dx.doi.org/10.1016/j.chaos.2009.03.043
[9] C. S. Liu, “Trial Equation Method to Nonlinear Evolution Equations with Rank Inhomogenous: Mathematical Discussions and Its Applications,” Communications in Theoretical Physics, Vol. 45, No. 2, 2006, pp. 219-223. http://dx.doi.org/10.1088/0253-6102/45/2/005
[10] C. S. Liu, “Trial Equation Method and its Applications to Nonlinear Evolution Equations,” Acta Physica Sinica, Vol. 54, No. 6, 2005, pp. 2505-2509.
[11] C. S. Liu, “Using Trial Equation Method to Solve the Exact Solutions for two kinds of KdV Equations with Variable Coefficients,” Acta Physica Sinica, Vol. 54, No. 10, 2005, p. 4506.
[12] C. S. Liu, “Representations and Classification of Traveling Wave Solutions to sinh-Gördon Equation,” Communications in Theoretical Physics, Vol. 49, No. 1, 2008, pp. 153-158. http://dx.doi.org/10.1088/0253-6102/49/1/33
[13] C. S. Liu, “Solution of ODE u'' + p(u)(u')2 + q(u) = 0 and Applications to Classifications of All Single Travelling Wave Solutions to Some Nonlinear Mathematical Physics Equations,” Communications in Theoretical Physics, Vol. 49, No. 2, 2008, pp. 291-296. http://dx.doi.org/10.1088/0253-6102/49/2/07
[14] C. S. Liu, “Applications of Complete Discrimination System for Polynomial for Classifications of Traveling Wave Solutions to Nonlinear Differential Equations,” Computer Physics Communications, Vol. 181, No. 2, 2010, pp. 317-324. http://dx.doi.org/10.1016/j.cpc.2009.10.006
[15] C. S. Liu, “Classification of All Single Travelling Wave Solutions to Calogero-Degasperis-Focas Equation,” Communications in Theoretical Physics, Vol. 48, No. 10, 2007, pp. 601-604. http://dx.doi.org/10.1088/0253-6102/48/4/004
[16] C. S. Liu, “All Single Traveling Wave Solutions to Nizhnok-Novikov-Veselov Equation,” Communications in Theoretical Physics, Vol. 45, No. 6, 2006, pp. 991-992. http://dx.doi.org/10.1088/0253-6102/45/6/006
NOTES

*Corresponding author.

