International Journal of Intelligence Science
Vol.05 No.02(2015), Article ID:53712,9 pages
10.4236/ijis.2015.52010
Biological Neural Network Structure and Spike Activity Prediction Based on Multi-Neuron Spike Train Data
Tielin Zhang1,2*, Yi Zeng1*, Bo Xu1
1Institute of Automation, Chinese Academy of Sciences, Beijing, China
2University of Chinese Academy of Sciences, Beijing, China
Email: zhangtielin2013@ia.ac.cn, yi.zeng@ia.ac.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 January 2015; accepted 23 January 2015; published 30 January 2015
ABSTRACT
The micro-scale neural network structure for the brain is essential for the investigation on the brain and mind. Most of the previous studies typically acquired the neural network structure through brain slicing and reconstruction via nanoscale imaging. Nevertheless, this method still cannot scale well, and the observation on the neural activities based on the reconstructed neural network is not possible. Neuron activities are based on the neural network of the brain. In this paper, we propose that multi-neuron spike train data can be used as an alternative source to predict the neural network structure. And two concrete strategies for neural network structure prediction based on such kind of data are introduced, namely, the time-ordered strategy and the spike co-occurrence strategy. The proposed methods can even be applied to in vivo studies since it only requires neural spike activities. Based on the predicted neural network structure and the spreading activation theory, we propose a spike prediction method. For neural network structure reconstruction, the experimental results reveal a significantly improved accuracy compared to previous network reconstruction strategies, such as Cross-correlation, Pearson, and the Spearman method. Experiments on the spikes prediction results show that the proposed spreading activation based strategy is potentially effective for predicting neural spikes in the biological neural net- work. The predictions on the neural network structure and the neuron activities serve as foundations for large scale brain simulation and explorations of human intelligence.
Keywords:
Neural Network Structure Prediction, Spike Prediction, Time-Order Strategy, Co-Occurrence Strategy, Spreading Activation

1. Introduction
The micro-scale brain anatomy and activities of the neurons are essential for understanding how the brain works and the nature of human intelligence. The general motivation of this paper comes from the fact that neuronal structure and activities are closely connected with each other even though it is usually very hard to get both neural anatomical structure and spike activity by electrophysiology or imaging method at the same time. The general idea is that even without nanoscale imaging techniques (which cannot scale well), it is still possible to reconstruct the neural network structure and predict spike activities by analyzing the spike train data.
From the structure perspective, we propose that multi-neuron spike train data can be used as an alternative source to predict the neural network structures, and here we discuss two concrete strategies for neural network structure prediction based on this kind of data. Multi-neuron spike train data is composed of spike trains from multiple neurons recorded in the same time interval. The data typically shows whether a specific neuron generates a spike or not at a specific time. Two strategies are proposed for neural network structure prediction: 1) the time-ordered strategy: synapses exist between neurons that generate spikes at the two neighborhood time points (i.e. the time point N and N-1); 2) the spike co-occurrence strategy: synapses exist between neurons that fire together at the same time slot. This strategy is consistent with the Hebb’s law “cells that fire together, wire together”.
From the function perspective, for each neuron in a neural network, its behavior is not only decided by its own property, but also very relevant to its contexts (e.g. other neurons in the same network). Hence, effective prediction of neural spike activities in a network context requires at least the following three major efforts: 1) response prediction of a single neuron towards a stimulus; 2) obtaining the detailed network structure, with synapse information among neurons; 3) modeling signal transmission based on the neural network. We use the neuron simulator to build detailed single pyramidal cells for the first effort. The network structure is built by the methods introduced above, while the spreading activation method based on the two previous efforts is introduced for the third effort. We use part of the spike train data to build the neural network structure and the model for neural activity prediction and the rest is for validation.
In order to validate the proposed methods and strategies, we use the data based on calcium imaging technology. Among different kinds of calcium imaging method, one of them is named functional Multi-neuron Calcium Imaging (fMCI), namely, multi-neurons loading of calcium fluorophores. The advantages of fMCI include: 1) recording en masse from hundreds of neurons in a wide area; 2) single-cell resolution; 3) identifiable location of neurons; and 4) detection of non-active neurons during the observation period. These advantages enables us acquire necessary spike train data discussed above to support the investigation and validation of proposed problems and methods. The paper is structured as follows: Section 2 briefly introduce related work, Section 3 explain the detailed neural network structure and spikes prediction method as well as their relationships, and Section 4 describes the experiments and results to show the prediction accuracy, finally conclusion is made in Section 5. This paper refines and extends the work introduced in [1] and [2] .
2. Related Work
From the structure perspective, most common approaches for obtaining the micro-level neural network structure is typically based on brain slicing and reconstruction with nanoscale imaging [3] [4] . This method can accurately locate the position of neurons, synapses and even dendritic spines. But at the same time, complex and weak nanoscale images make image repairing, synapse recognition and 3D structure reconstruction cost too much time. Based on current brain slicing and imaging techniques, it is still difficult to get synaptic scale neural network structures for a small group of neurons, let alone bigger network. In addition, tissues after slicing are with no functional reactions any more. This makes advanced research on neuronal functions based on the reconstructed neural network nearly impossible.
From the activity perspective at the nanoscale, electrophysiology techniques and calcium imaging techniques are frequently used. The electrophysiology techniques detect and save the neurons’ time dependent soma voltage [5] . This technique is with accurate temporal resolution but poor space resolution. In addition, it can only record few neurons’ voltage at one time. While calcium fluorescence imaging techniques detect the changes on neurons’ voltage values by monitor cell calcium changes, it can monitor the activity of a hundred to thousand neurons simultaneously both in vitro and in vivo [6] . The maximum number of neurons monitored by calcium fluorescence is around 100,000 cells for zebrafish [7] . Stetter uses transfer entropy method to reconstruct the network which requires no prior statistics and connections assumptions, and the work focuses on excitatory synaptic links, and network clustering topology [8] . Takahashi investigates the calcium imaging experiments including imaging, spikes detection and some network analysis tasks. He and coauthors conclude that the network fits for power-law scaling of synchronization properties and network connection probability varies from different network scales [6] .
3. Methodology
Although the functional data are collected by functional multi-neuron calcium imaging techniques, the missing of relevant structures from anatomical method still makes analysis about the dynamic causality for the whole network hard. Here we propose architecture to analyze the spike train data to predictively reconstruct the micro- level network structure, and predict neuronal activities based on the reconstructed network.
The methodology introduced here relies on spike train data generated by various kinds of techniques (e.g. fMCI and electrophysiology experiments). In this paper, we use the experimental data from the mouse memory task [6] . Spontaneous spiking activities are still happening in slices of the mouse brain hippocampus CA1 area when it was taken out of the body for not a long time. These spikes show the special task related network function in hippocampus, such as memory retention. The understanding of these kinds of data can greatly speed up the procedure of memory research.
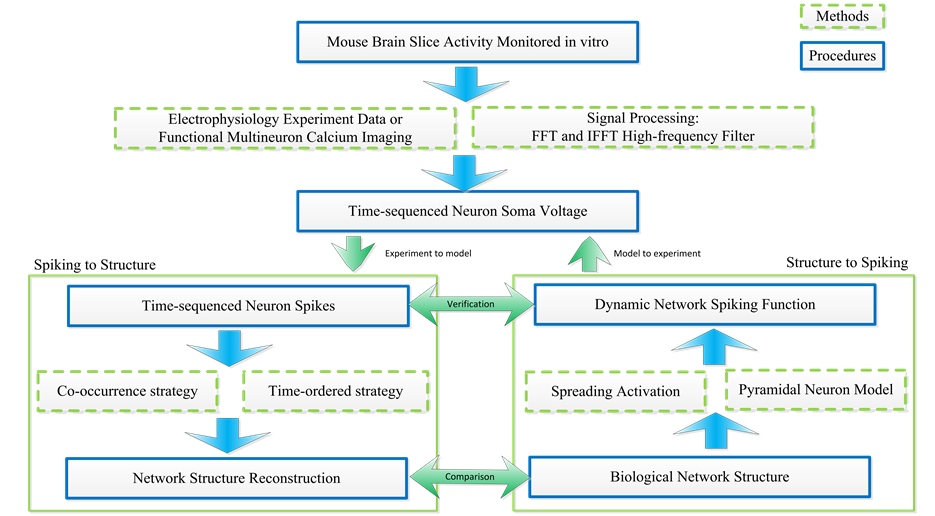
As Figure 1 shows, calcium images and neuron voltages from mouse slices data are collected by fMCI me- thod. Neural voltage signals based on the fMCI technique are with low Signal to Noise Ratio (SNR). Hence, signal processing to filter noise is necessary. Here we use Fast Fourier Transform (FFT) and Inverse Fast Fourier Transform (IFFT) methods to filter the high frequency noises so that spiking signals can be detected precisely. Then two methods to convert neural spike signals to neural structure are introduced, namely, the co-occurrence strategy and the time-ordered strategy. As a step forward, we propose a spike activity prediction method based on the predicted neural network, the spreading activation theory and single pyramidal neuron models.
3.1. Voltages Signal Processing
Voltages signals from calcium imaging are so closed combined with noise that high frequency filter must be applied for further spikes detection. The processing procedure mainly includes the following four parts: 1) using FFT to transform time sequence signals to frequency signals; 2) using high frequency filters to eliminate signal
Figure 1. The overall architecture for predicting neural network structure and neuronal activities based on spike train data.
noises; 3) using IFFT to transform frequency signals back to time series signals; 4) deciding the voltage threshold to detect spiking signals. As Figure 2 shows, after signal transformation from time series to frequency and back again by FFT and IFFT, high frequency noises are filtered and spike signals are detected.
3.2. From Spikes to Neuronal Structures
In this paper, two strategies are discussed and used to realize the procedure of converting spike signals to neural network structure:
1) The time-ordered strategy: synapses exist between neurons that generate spikes at the two neighborhood time points (the time point N and N-1);
2) The spike co-occurrence strategy: synapses exist between neurons that fire together at the same time slot. This strategy is consistent with the Hebb’s law “cells that fire together, wire together”.
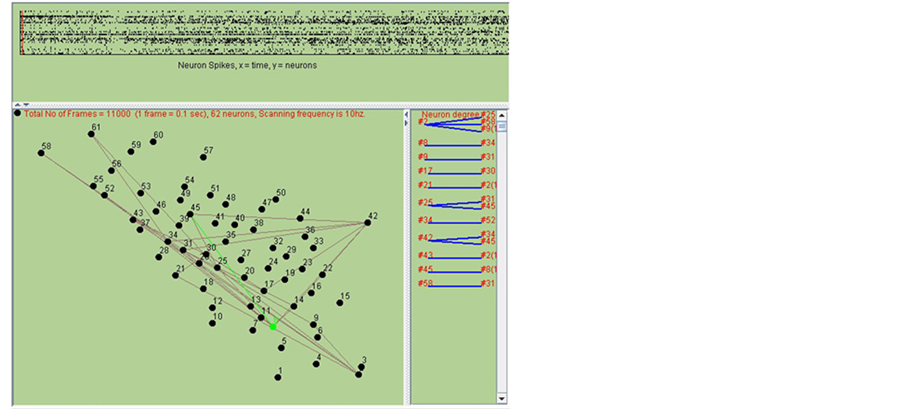
Based on the proposed two different strategies, two neurons that may share a connection might be connected from tens to hundreds of times. Each time of connection is with the same unit strength. However, more times of connection between neurons indicate the higher probability for the existence of synapse. As shown in Figure 3, the network is rebuilt by combination of two methods. The upper panel in Figure 3 shows the spikes states of 62
Figure 2. Neural activity signal processing. a) Original time series signals; b) FFT frequency signals; c) High frequency filter; d) IFFTtime series signals; e) Signal smooth process; f) Voltage threshold method of spiking detection.
Figure 3. Network structure prediction procedure.
neurons in different time slot. The bottom left panel shows the present spike transfer (in green line). The bottom right panel shows the connection probability of different neurons.
3.3. Spike Prediction Based on Spreading Activation
With the reconstructed micro-level neural network based on the methods proposed in Section 3.2, combined with single neuron models, we can predict spike activities for the neurons in observation. Here we first introduce a single neuron model as a foundation. Then we propose a spreading activation based spike prediction method, which utilize the single neuron model and the predicted neural network.
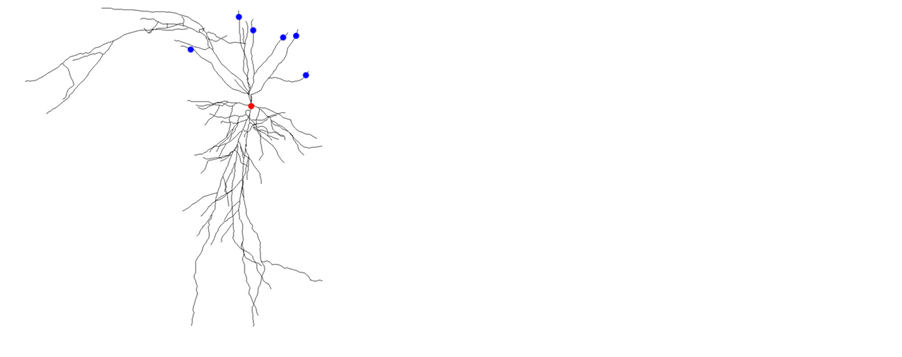
Since pyramidal neuron is widely distributed in mouse hippocampus (more than 90%) [9] , here we introduce the single neuron model of a kind of pyramidal neuron in mouse brain hippocampus CA1 area for the simulation of the neuronal activities. Its neural structure obtained from http://neuromorpho.org/ (ID: NMO_08800) is shown in Figure 4(a). Neuron model contains three basic kinds of ion channels, namely potassium channel, sodium channel and calcium channel. Potassium ion channels mainly include four subtypes, namely K+-A+ channel, ba- sic potassium channel, slow Ca2+-dependent potassium channel and calcium-activated potassium channel. The calcium ion channel contains l-calcium channel and basic calcium channel. The sodium ion channel is H-current kind of sodium channel. In addition, detailed ion channel parameters in different model sections such as soma, axon and dendrite are varied from each other. Neuron response with given voltage stimuli is shown in Figure 4(b). Special response from high stimuli voltage can be found in Figure 4(c), which shows the detailed neuron model with more ion channels (not only basic H-H kind of Na+, K+, Ca2+), not just leaky integrate-and-fire kind of spiking model. It is able to describe the property of neuronal refractory period well in this model. This detailed pyramidal neuron model built in neuron [10] [11] is essential to understanding and simulation of brain network function.
Spreading activation (SA) was proposed in cognitive psychology for understanding human memory. It is also widely used for searching associative network, neural network or semantic network [12] . The SA network is briefly illustrated in Figure 5. In this paper, this method is applied to the micro scale for understanding neural network activities and predicting spikes.

Figure 4. Single pyramidal cell’s reaction with voltage stimulus (0.1 nA to 1 nA). The morphology of the pyramidal cell (a) is from http://neuromorpho.org/ (ID: NMO_08800).
Figure 5. An illustration of the SA network mechanism.
Here we utilize some biology evidence to enhance SA method. The two important variables in SA is the de- cay factor D and the voltage threshold F. As Figure 6 shows, electrical stimulation action experiment is simu- lated by Neuron software on real pyramidal cell in mouse hippocampus CA1 area introduced above. Both vol- tages in soma and dendrites are monitored. As Equation (1) shows, since the voltage decay between two neurons is mainly caused by dendrites instead of axons, we can calculate the average voltage decay range as the univer- sal decay which is fit for the decay factor in SA method. Based on the calculation, the value of D should be 0.22. As Equation (2) shows, voltage threshold F can be the neuron spiking threshold which is set as −56 mv based on [13] .
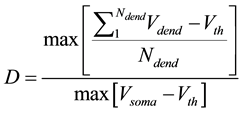 (1)
(1)
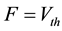 (2)
(2)
D is the decay factor in SA method which can be biologically described as the voltage decay.
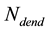 is the number of neuronal dendrites.
is the number of neuronal dendrites.
 is the voltage of the dendrite section.
is the voltage of the dendrite section.
 is the resting potential of neuron. F, which represents the spreading threshold factor in SA, is described by pyramidal cell voltage threshold.
is the resting potential of neuron. F, which represents the spreading threshold factor in SA, is described by pyramidal cell voltage threshold.
The SA method is initiated by activating some neurons as source nodes and then iteratively propagates or spreads that activation to other neurons. During the propagation procedure, the values from original neurons de- cay according to different weights of neighbor neurons. The activation will terminate when the values go below the threshold for activation [12] . The detailed SA based method for spike prediction is described as follows.
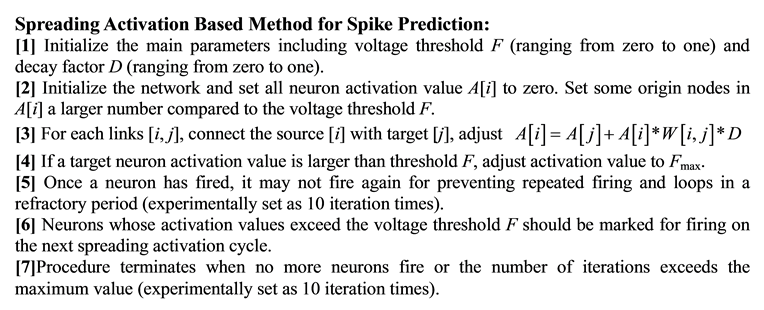
4. Experiments and Results
4.1. The Pathway Prediction Results
Data of the rat hippocampus CA1 pyramidal cell layer based on fMCI is used for neural network structure prediction (including 8 datasets, and each of them records spike activities for 62 to 226 neurons. The datasets were imaged with the frequency of 10 Hz [6] [14] ) using the upper two proposed strategies.
We validate the accuracy of the neural network structure prediction strategies based on the following steps. The overall prediction accuracy is an average value based on the 8 dataset. For each of the dataset: 1) Equally divide one dataset as 20 sub datasets according to the time intervals (The sub datasets are denoted as S1,…,S20). Select the first 80% of the sub datasets (S1,…,S16) for neural network structure construction, and validate the pathway using the rest of the 20% sub dataset (Here we assume that if the predicted pathway is correct, it should cover the neuronal connections based on the rest of the 20% sub datasets); 2) Select another 80% of the sub da- tasets for neural network structure construction, and the rest for validation, and repeat this step until all the sub datasets have been selected for validation. 3) The prediction accuracy is the average value of the 20 predictions.
There are several important observations and indications based on the prediction results. 1) Although the two prediction strategies seem entirely different, the neural network structures based on the two different strategies are very relevant (The correlation is significant with the Pearson correlation value 0.958). It indicates that al-
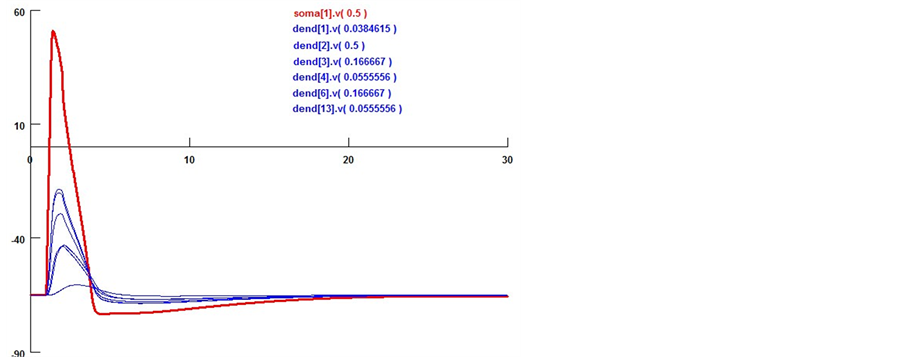
Figure 6. Pyramidal cell morphology and electrical activity simulation. a) Single pyramidal cell voltage, probe method to ensure the section voltages in soma (red point) and dendrites (blue points); b) Different synapse sections and soma voltage changing by multi stimuli from six neurons. Both soma [i], v[j] and dendrite [i], v[j] sections are built in this model, i stands for the section id, j denotes the detection probe position. The average decay factor is calculated by means of these six voltages.
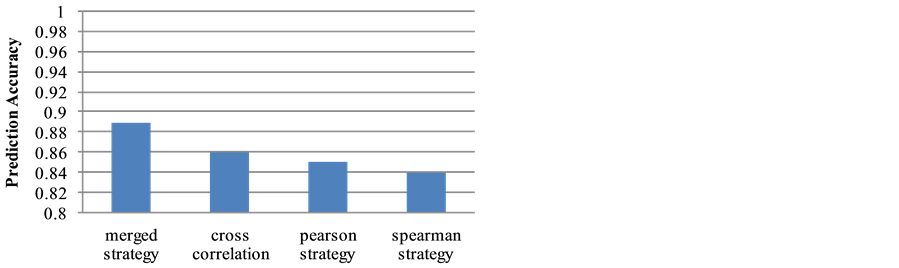
though the proposed strategies are different, the results from the two different strategies do not have major conflicts, instead they are very consistent, and support each other. 2) The neural network structure prediction accuracy for the time-ordered strategy is 83.4%, and the accuracy for the spike co-occurrence strategy is 80.5%. When we group the two neural network structures together (denoted as the merged strategy), the prediction accuracy reaches 89.3%. Figure 7 shows the prediction accuracy for each of the dataset using the proposed strategies. This result indicates that better prediction can be made when the predicted pathways from the two strategies are combined together. 3) 27% of the possible connections among neurons are selected for the time-or- dered strategy, while 25% of the connections are selected by the spike co-occurrence strategy. If the two results are grouped together, 32% of the possible connections are included. The results seem good, since the coverage is not high (and is consistent with the observation by using electro-microscopy techniques [15] [16] ), while the predicted accuracy for possible neural network structure reaches 89%. Comparing with other correlation strategies, merged strategy shows better prediction accuracy results as Figure 8 shows.
The proposed method is validated on the data in which the distance of two neurons is within approximately 400 μm [17] . Whether the proposal is applicable when the distance goes further needs to be validated. In addition, our current result is based on fMCI data from rat brain slices. In our future work, we will investigate the possibility of using the proposed method on fMCI in-vivo imaging data.
4.2. Spike Prediction Results
Assume a specific neuron (denoted as n1) is connected with N neurons in the network and its action potential is V, the post synaptic neurons of n1 receive transmitted signals from n1. When one synaptic transmission is done and the signal reaches the post synaptic soma, its contribution to this soma is around 5 mv [18] . The overall contribution to the voltage of the soma (denoted as P) is represented as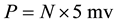 , which is obtained by summing up all the contribution from each of the post synaptic potential, while P is used as the stimulus to generate next action potentials. Each of the potential P for the N neurons that connects to a specific neuron can be obtained through the upper calculation process. Having the structure of the neural network, we predict the neuron which owns the largest value of P will generate a spike in a refractory period (experimentally set as 10 iteration times).
, which is obtained by summing up all the contribution from each of the post synaptic potential, while P is used as the stimulus to generate next action potentials. Each of the potential P for the N neurons that connects to a specific neuron can be obtained through the upper calculation process. Having the structure of the neural network, we predict the neuron which owns the largest value of P will generate a spike in a refractory period (experimentally set as 10 iteration times).
In order to validate the proposed method, the data from the rat hippocampus CA1 pyramidal cell layer using fMCI is used (including 8 datasets, and each of them records spike activities from 62 to 226 neurons. The datasets were pictured with the frequency of 10 Hz [6] [14] ). Since the time slot during two neighborhood pictures is 100 ms, signal transmissions may have looped for several rounds. Hence, iterations of the spreading activation process are needed. The spike prediction accuracy for each of the dataset is shown in Figure 9.
Figure 7. Neural pathway prediction accuracy based on fMCI multi-neuron spike train dataset.
Figure 8. Accuracy made by the merged strategy and other correlation strategies.
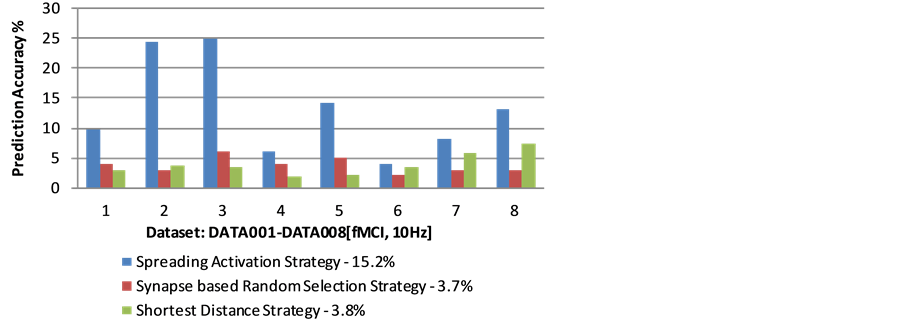
Figure 9. Neural spike prediction accuracy based on different strategies.
As a comparative study, we introduce two alternative strategies, namely the shortest distance strategy (the neuron which owns the shortest distance compared to other post synaptic neurons will be fired), and the synapse based random selection strategy (randomly select a neuron from the set of post synaptic neurons). As shown in Figure 1, the spreading activation based strategy outperforms other two strategies and the average prediction accuracy on 8 datasets is around 15.2%, at least three times better than the other two strategies (the average prediction accuracy for shortest distance strategy is 3.8%, while the synapse based random selection strategy is 3.7%). The validation shows that the proposed spreading activation strategy is potentially effective for predicting neural spikes in the neural network.
5. Conclusion
In this paper, two strategies to predict neural network structure ares proposed and high accuracy experiment results are showed in Section 4.1 and proved their efficiency. This effort makes the rebuilt network structure without anatomy slicing possible. Although restricted by the experimental data, the size of the rebuilt network is around hundred neurons, it still shows great potential for handling larger network reconstruction tasks. Further, the spiking prediction method gives us a view point to analyze the special condition in which we can acquire only structure data. As the first try, this paper only compared with some commonly used methods, such as cross correlation, Pearson and Spearman strategies. More methods will be taken into consideration for comparative studies in the future, such as Granger causality method. One further potential efforts for this work is that spiking functional activities from prediction model can further be used to guide biological experiment signal processing, such as which kind of spikes are noises while others are not.
Acknowledgements
This paper is supported by the Brain Engineering project funded by Institute of Automation, Chinese Academy of Sciences. The authors would like to thank anonymous reviewers for constructive comments.
References
- Zeng, Y., Zhang, T.L. and Xu, B. (2014) Neural Pathway Prediction Based on Multi-Neuron Spike Train Data. Proceedings of the 23rd Annual Computational Neuroscience Meeting (CNS 2014), Québec City, 26-31 July 2014, 6.
- Zhang, T.L., Zeng, Y. and Xu, B. (2014) Neural Spike Prediction Based on Spreading Activation. Proceedings of the 23rd Annual Computational Neuroscience Meeting (CNS 2014), Québec City, 26-31 July 2014, 7.
- Sporns, O., Tononi, G. and Kötter, R. (2005) The Human Connectome: A Structural Description of the Human Brain. PLoS Computational Biology, 1, e42. http://dx.doi.org/10.1371/journal.pcbi.0010042
- Arenkiel1, B.R. and Ehlers, M.D. (2009) Molecular Genetics and Imaging Technologies for Circuit-Based Neuroanatomy. Nature, 461, 900-907. http://dx.doi.org/10.1038/nature08536
- Mukamel, R. and Fried, I. (2011) Human Intracranial Recordings and Cognitive Neuroscience. Annual Review of Psychology, 63, 511-537. http://dx.doi.org/10.1146/annurev-psych-120709-145401
- Takahashi, N., Sasaki, T., Usami, A., Matsuki, N. and Ikegaya, Y. (2007) Watching Neuronal Circuit Dynamics through Functional Multineuron Calcium Imaging (fMCI). Neuroscience Research, 58, 219-225. http://dx.doi.org/10.1016/j.neures.2007.03.001
- Kettunen, P. (2012) Calcium Imaging in the Zebrafish. In: Islam, S., Ed., Calcium Signaling, Springer Netherlands, Heidelberg, 1039-1071.
- Stetter, O., Battaglia, D., Soriano, J. and Geisel, T. (2012) Model-Free Reconstruction of Excitatory Neuronal Connectivity from Calcium Imaging Signals. PLoS Computational Biology, 8, e1002653. http://dx.doi.org/10.1371/journal.pcbi.1002653
- Mira, J. and Sánchez-Andrés, J.V. (1999) Foundations and Tools for Neural Modeling. Proceedings of International Work-Conference on Artificial and Natural Neural Networks, Vol. I, Alicante, 2-4 June 1999, 29.
- Carnevale, N.T. and Hines, M.L. (2006) The Neuron Book. Cambridge University Press, Cambridge, UK. http://dx.doi.org/10.1017/CBO9780511541612
- Dayan, P. and Abbott, L.F. (2001) Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. MIT Press, Cambridge.
- Anderson, J.R. (1983) A Spreading Activation Theory of Memory. Journal of Verbal Learning and Verbal Behavior, 22, 261-295. http://dx.doi.org/10.1016/S0022-5371(83)90201-3
- Yue, C.Y., Remy, S., Su, H.L., Beck, H. and Yaari, Y. (2005) Proximal Persistent Na+ Channels Drive Spike Afterdepolarization and Associated Bursting in Adult CA1 Pyramidal Cells. The Journal of Neuroscience, 25, 9704-9720. http://dx.doi.org/10.1523/JNEUROSCI.1621-05.2005
- Yue, C.Y., Remy, S., Su, H.L., Beck, H. and Yaari, Y. (2011) High-Speed Multi-Neuron Calcium Imaging Using Nipkow-Type Confocal Microscopy. Current Protocols in Neuroscience, 2, Unit 2.14. http://www.hippocampus.jp/data
- Gómez-Di Cesare, C.M., Smith, K.L., Rice, F.L. and Swann, J.W. (1997) Axonal Remodeling during Postnatal Maturation of CA3 Hippocampal Pyramidal Neurons. Journal of Comparative Neurology, 384, 165-180.
- Fujisawa, S., Matsuki, N. and Ikegaya, Y. (2006) Single Neurons Can Induce Phase Transitions of Cortical Recurrent Networks with Multiple Internal States. Cerebral Cortex, 16, 639-654. http://dx.doi.org/10.1093/cercor/bhj010
- Sasaki, T., Matsuki, N. and Ikegaya, Y. (2007) Metastability of Active CA3 Networks. The Journal of Neuroscience, 27, 517-528. http://dx.doi.org/10.1523/JNEUROSCI.4514-06.2007
- Lodish, H., Berk, A., Zipursky, S.L., Matsudaira, P., Baltimore, D. and Darnell, J. (2000) Molecular Cell Biology. 4th Edition, Freeman and Company, New York.
NOTES
*These authors contributed to the work equally and should be regarded as co-first authors.