International Journal of Intelligence Science
Vol.3 No.2(2013), Article ID:30636,8 pages DOI:10.4236/ijis.2013.32012
The Sound and Complete R-Calculi with Respect to Pseudo-Revision and Pre-Revision*
1State Key Laboratory of Software Development Environment, Beijing University of Aeronautics and Astronautics, Beijing, China
2Key Laboratory of Intelligent Information Processing, Institute of Computing Technology, Chinese Academy of Sciences, Beijing, China
Email: liwei@nlsde.buaa.edu.cn, yfsui@ict.ac.cn
Copyright © 2013 Wei Li, Yuefei Sui. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 18, 2013; revised February 20, 2013; accepted March 15, 2013
Keywords: Belief Revision; R-Calculus; Maximal Consistent Set; Pseudo-Revision; Pre-Revision
ABSTRACT
The AGM postulates ([1]) are for the belief revision (revision by a single belief), and the DP postulates ([2]) are for the iterated revision (revision by a finite sequence of beliefs). Li [3] gave an R-calculus for R-configurations  where Δ is a set of literals, and Γ is a finite set of formulas. We shall give two
where Δ is a set of literals, and Γ is a finite set of formulas. We shall give two 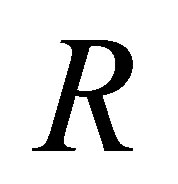 -calculi such that for any consistent set Γ and finite consistent set
-calculi such that for any consistent set Γ and finite consistent set  of formulas in the propositional logic, in one calculus, there is a pseudo-revision Θ of Γ by Δ such that
of formulas in the propositional logic, in one calculus, there is a pseudo-revision Θ of Γ by Δ such that  is provable and
is provable and 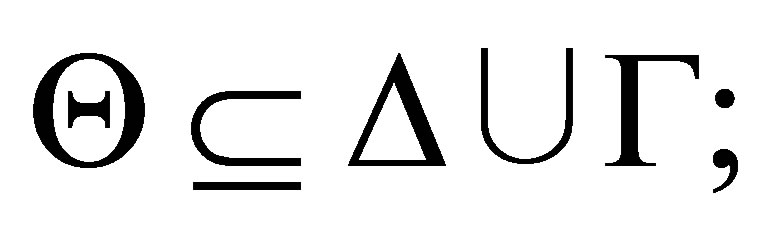 and in another calculus, there is a pre-revision Ξ of Γ by Δ such that
and in another calculus, there is a pre-revision Ξ of Γ by Δ such that 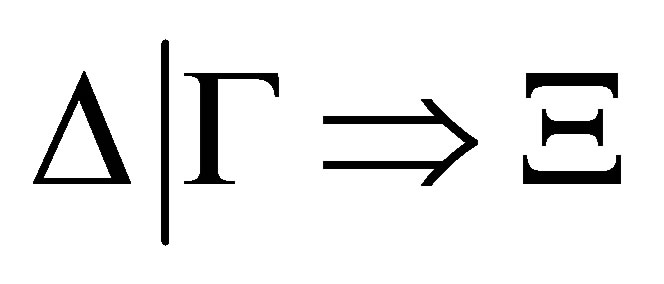 is provable,
is provable, 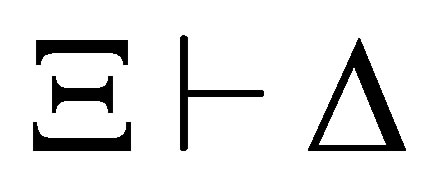 and
and 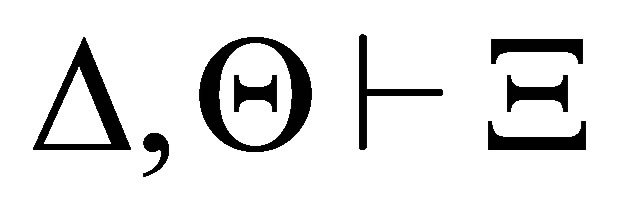 for some pseudo-revision Θ; and prove that the deduction systems for both the
for some pseudo-revision Θ; and prove that the deduction systems for both the  -calculi are sound and complete with the pseudo-revision and the pre-revision, respectively.
-calculi are sound and complete with the pseudo-revision and the pre-revision, respectively.
1. Introduction
The AGM postulates ([1],[4-6]) are for the revision 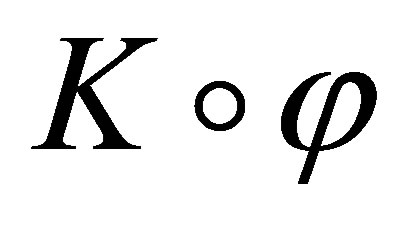 of a theory
of a theory  by a formula
by a formula  and the DP postulates ([2]) are for the iterated revision
and the DP postulates ([2]) are for the iterated revision 
The  -calculus ([3]) gave a Gentzen-type deduction system to deduce a consistent theory
-calculus ([3]) gave a Gentzen-type deduction system to deduce a consistent theory 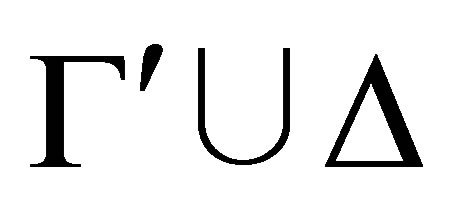 from any theory
from any theory  where
where 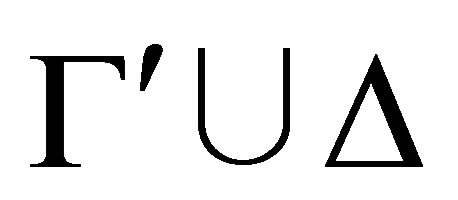 should be a maximal consistent subtheory of
should be a maximal consistent subtheory of  which includes
which includes  as a subset, where
as a subset, where  is an
is an  -configuration,
-configuration,  is a consistent set of formulas, and
is a consistent set of formulas, and  is a consistent sets of literals (atomic formulas or the negation of atomic formulas). It was proved that if
is a consistent sets of literals (atomic formulas or the negation of atomic formulas). It was proved that if 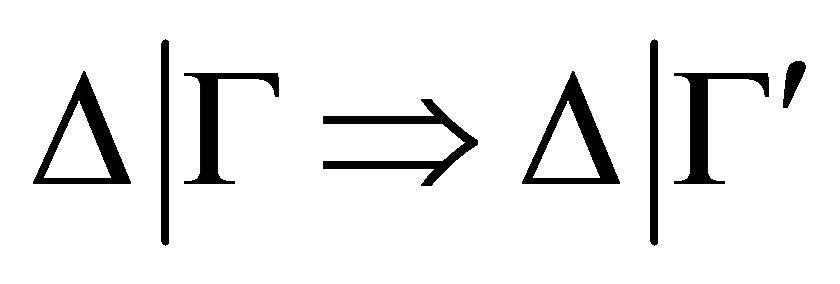 is deducible and
is deducible and  is an
is an 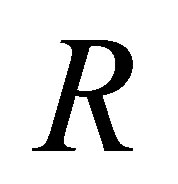 -termination, i.e., there is no
-termination, i.e., there is no 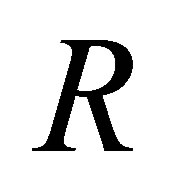 -rule to reduce
-rule to reduce 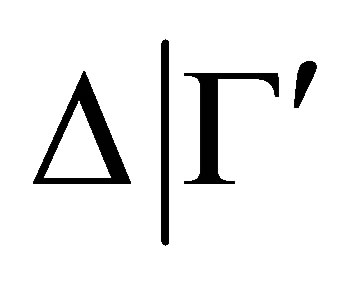 to another
to another 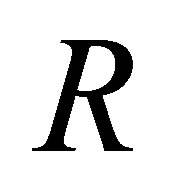 -configuration
-configuration 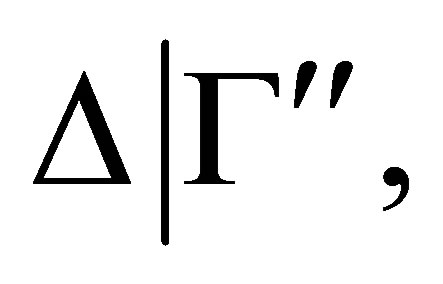 then
then 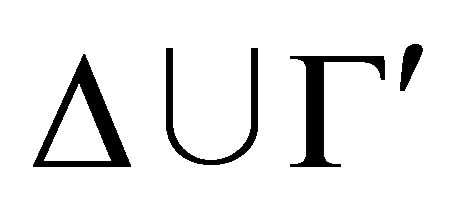 is a pseudo-revision of
is a pseudo-revision of  by
by 
The  -calculus has the following features:
-calculus has the following features:
●  is a finite set of literals (propositional variables or the negation of propositional variables);
is a finite set of literals (propositional variables or the negation of propositional variables);
●  is a set of formulas;
is a set of formulas;
●  are not sufficient for pseudo-revision, and
are not sufficient for pseudo-revision, and  is introduced to deduce
is introduced to deduce  into a consistent set
into a consistent set  of formulas including
of formulas including 
● the soundness theorem holds, that is, if 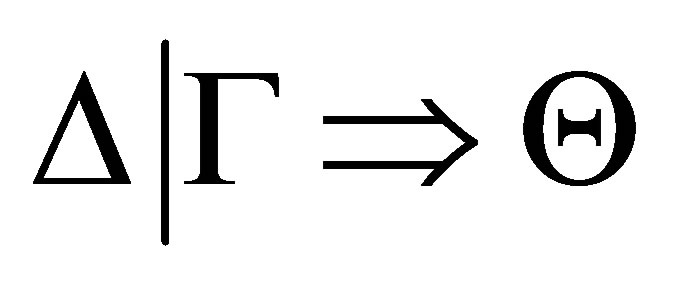 is provable then
is provable then  is a pseudo-revision of
is a pseudo-revision of  by
by  and
and
● the completeness theorem holds, that is, if  is a pseudo-revision of
is a pseudo-revision of  by
by  then
then 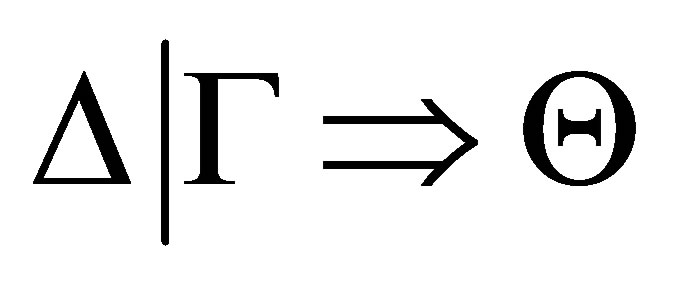 is provable.
is provable.
Because each rule in the 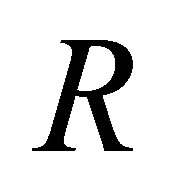 -calculus consists of the statements of form
-calculus consists of the statements of form
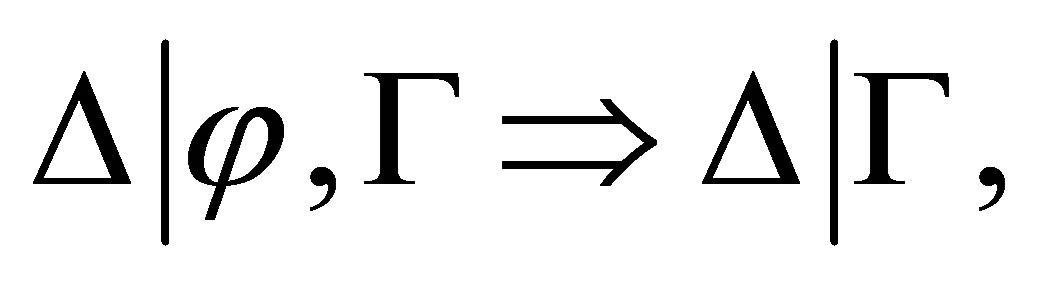
the 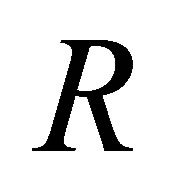 -calculus is based on pseudo-revision, i.e., to contract
-calculus is based on pseudo-revision, i.e., to contract  from
from  if
if  is inconsistent, which makes the
is inconsistent, which makes the 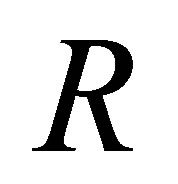 -calculus not preserve the minimal change principle.
-calculus not preserve the minimal change principle.
Given two theories  and
and 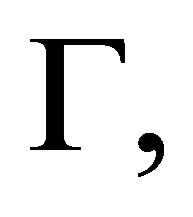 a pseudo-revision
a pseudo-revision  of
of 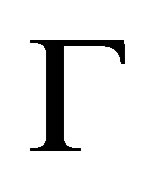 by
by  is a consistent subset of
is a consistent subset of  including
including  (if
(if 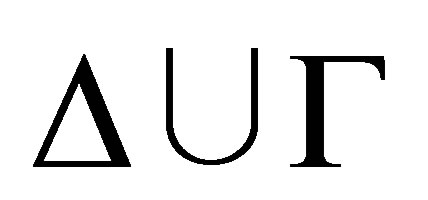 is inconsistent; otherwise,
is inconsistent; otherwise, ).
).
We shall give two 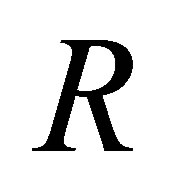 -calculi such that
-calculi such that
● in one 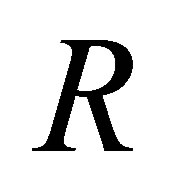 -calculus, say
-calculus, say 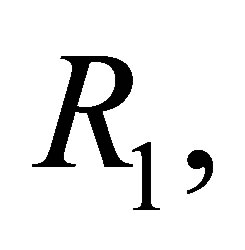 for any consistent formula set
for any consistent formula set  and finite formula set
and finite formula set  there is a consistent formula set
there is a consistent formula set 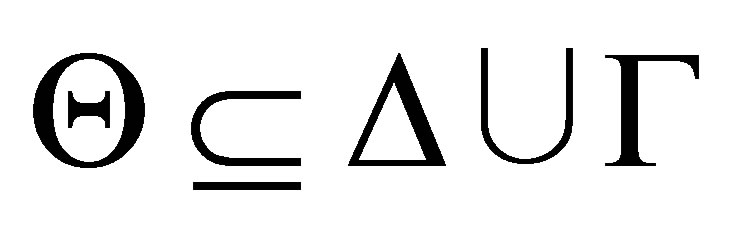 such that
such that 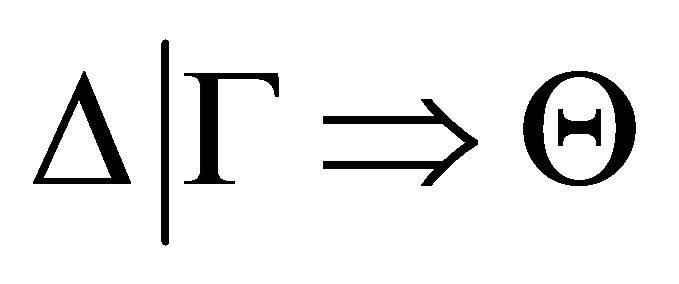 is provable and
is provable and  is a pseudo-revision of
is a pseudo-revision of  by
by  (the soundness theorem); and conversely, given any pseudo-revision
(the soundness theorem); and conversely, given any pseudo-revision  of
of  by
by  is provable (the completeness theorem);
is provable (the completeness theorem);
● in another  -calculus, say
-calculus, say 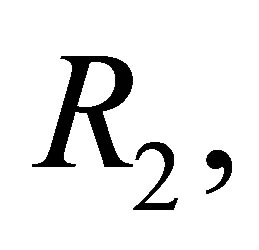 for any consistent formula set
for any consistent formula set  and finite formula set
and finite formula set 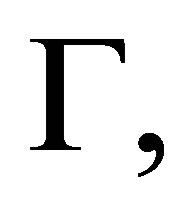 there are consistent formula sets
there are consistent formula sets  and
and  such that
such that
◦  is provable
is provable
◦  is a pseudo-revision of
is a pseudo-revision of  by
by 
◦ 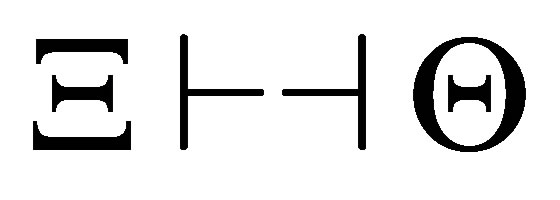 and
and
◦ there is no subformula  of
of  contradictory to
contradictory to  (the soundness theorem);
(the soundness theorem);
and conversely, given any pseudo-revision  of
of  by
by  there is a consistent formula set
there is a consistent formula set  such that
such that 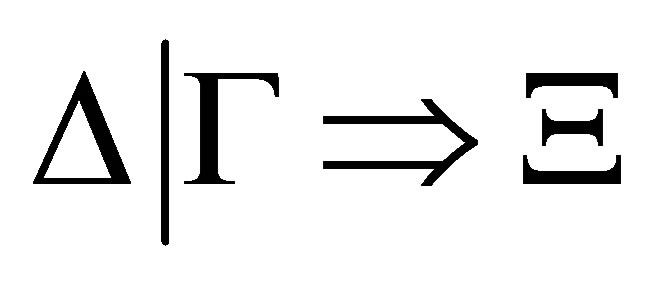 is provable,
is provable, 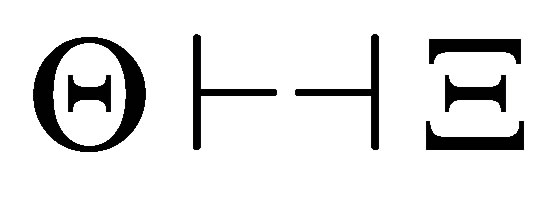 and
and  is contradictory to no subformula
is contradictory to no subformula  of
of  (the completeness theorem).
(the completeness theorem).
The 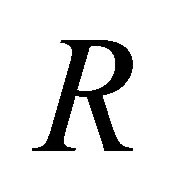 -calculi are different from the
-calculi are different from the  -calculus in [3] as follows:
-calculus in [3] as follows:
◊  is any set of formulas;
is any set of formulas;
◊ The cut-rule in the  -calculus is eliminated in the
-calculus is eliminated in the  -calculi;
-calculi;
◊ Because 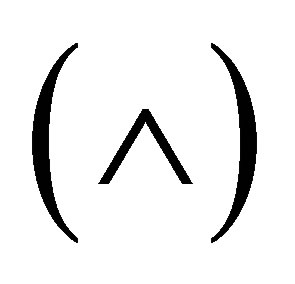 -rule in the
-rule in the 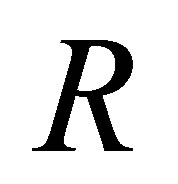 -calculus is not sufficient for reducing
-calculus is not sufficient for reducing
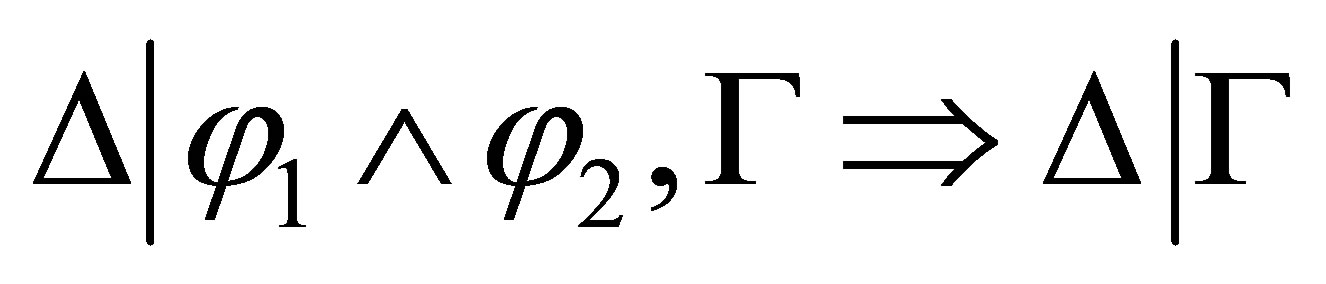
to either 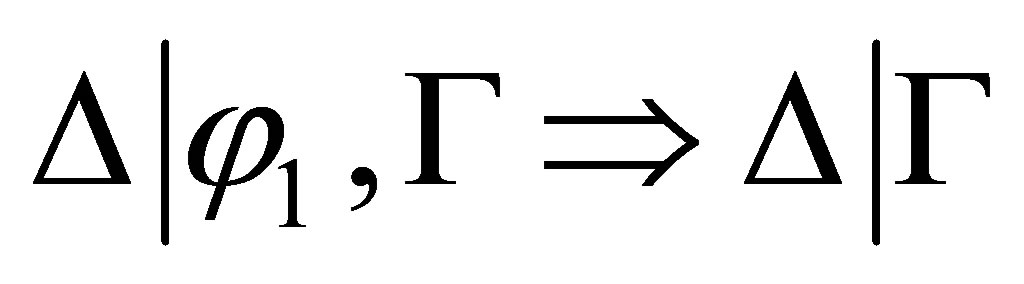 or
or  the
the  - calculus is not complete with respect to the pseudorevision of
- calculus is not complete with respect to the pseudorevision of  by
by  In the new
In the new  -calculi, we split
-calculi, we split 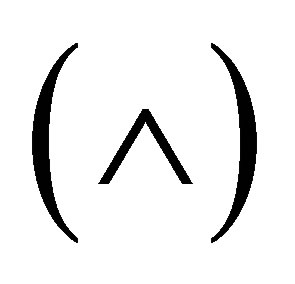 into two deduction rules
into two deduction rules 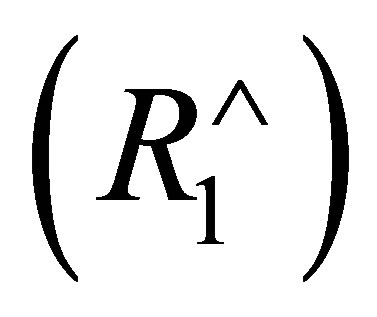 and
and 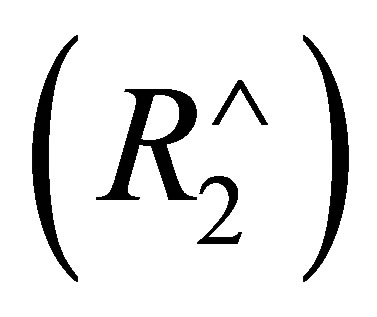 according to whether
according to whether  is consistent with
is consistent with  or not. The reason is given as follows.
or not. The reason is given as follows.
Given a consistent theory  and formulas
and formulas
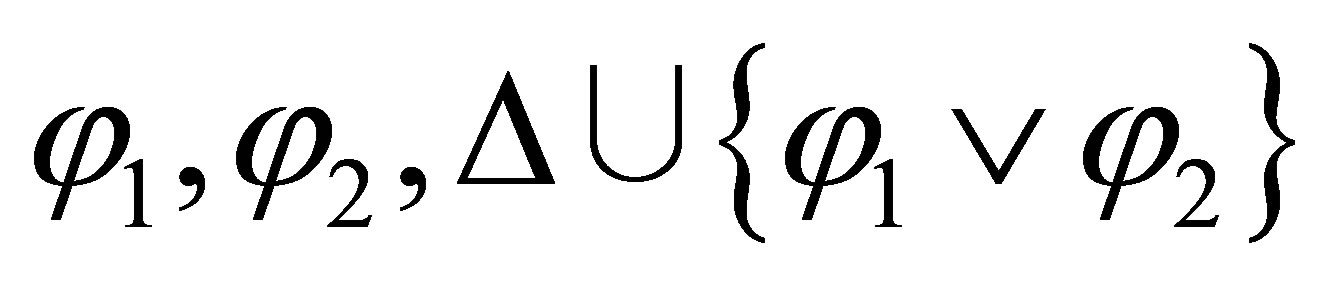 is inconsistent if and only if
is inconsistent if and only if
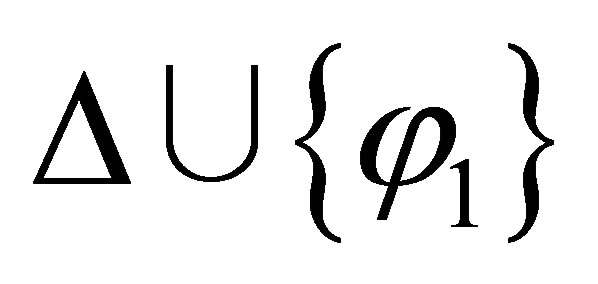 and
and 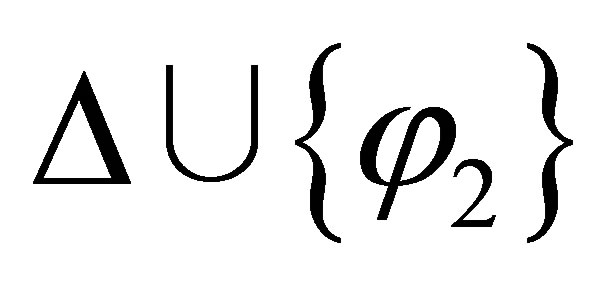 are inconsistent; and if either
are inconsistent; and if either 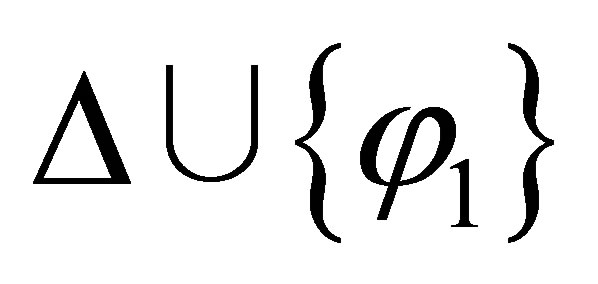 or
or 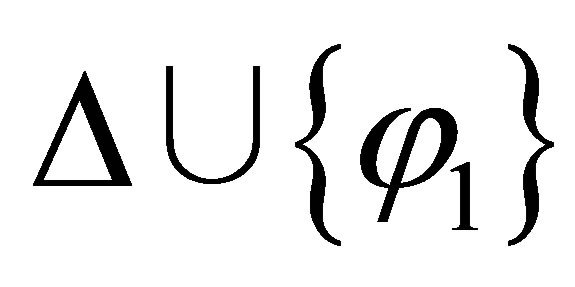 is inconsistent then
is inconsistent then 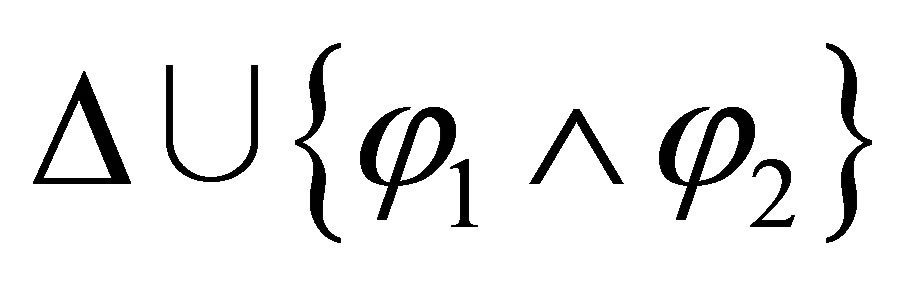 is inconsistent; and if
is inconsistent; and if 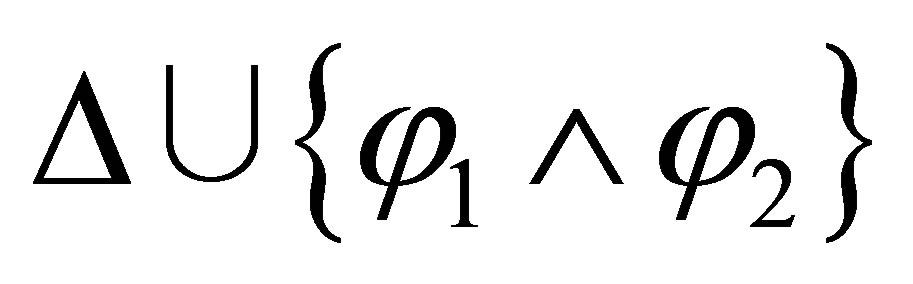 is inconsistent then we cannot deduce that either
is inconsistent then we cannot deduce that either 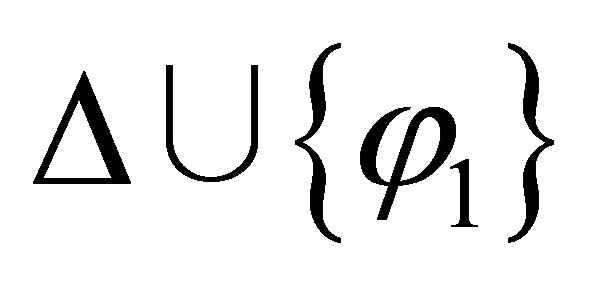 or
or 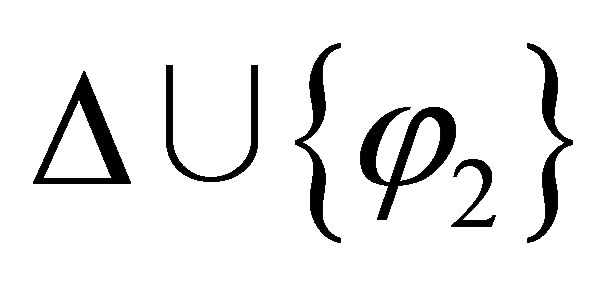 is inconsistent, and what we have is that
is inconsistent, and what we have is that  is inconsistent if and only if either
is inconsistent if and only if either 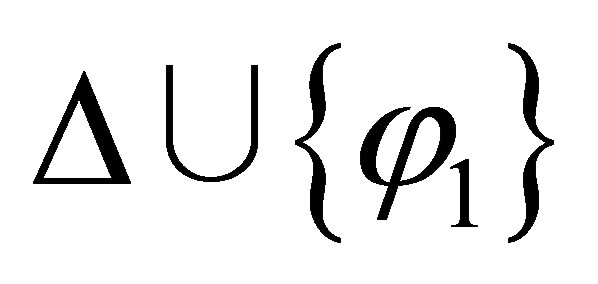 is inconsistent or
is inconsistent or  is inconsistent. Formally,
is inconsistent. Formally,
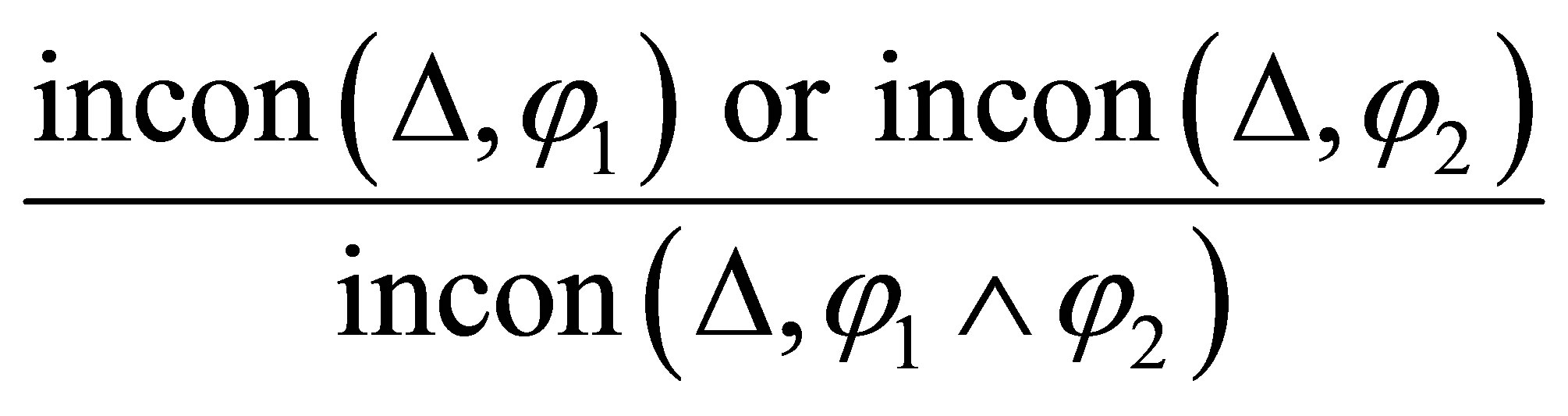 (1)
(1)
 (2)
(2)
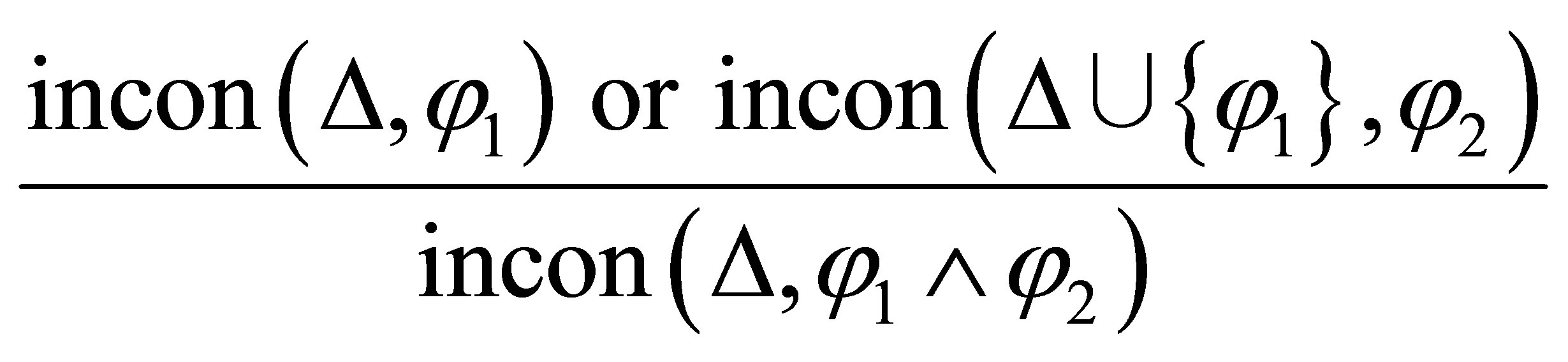 (3)
(3)
where 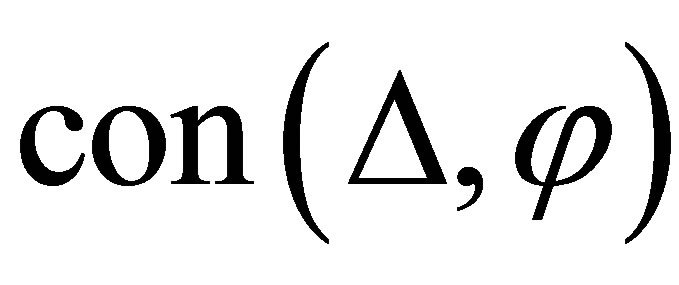 and
and  denote that
denote that 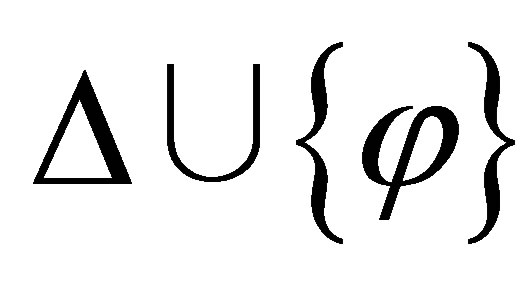 is consistent and inconsistent, respectively. Therefore, we use
is consistent and inconsistent, respectively. Therefore, we use
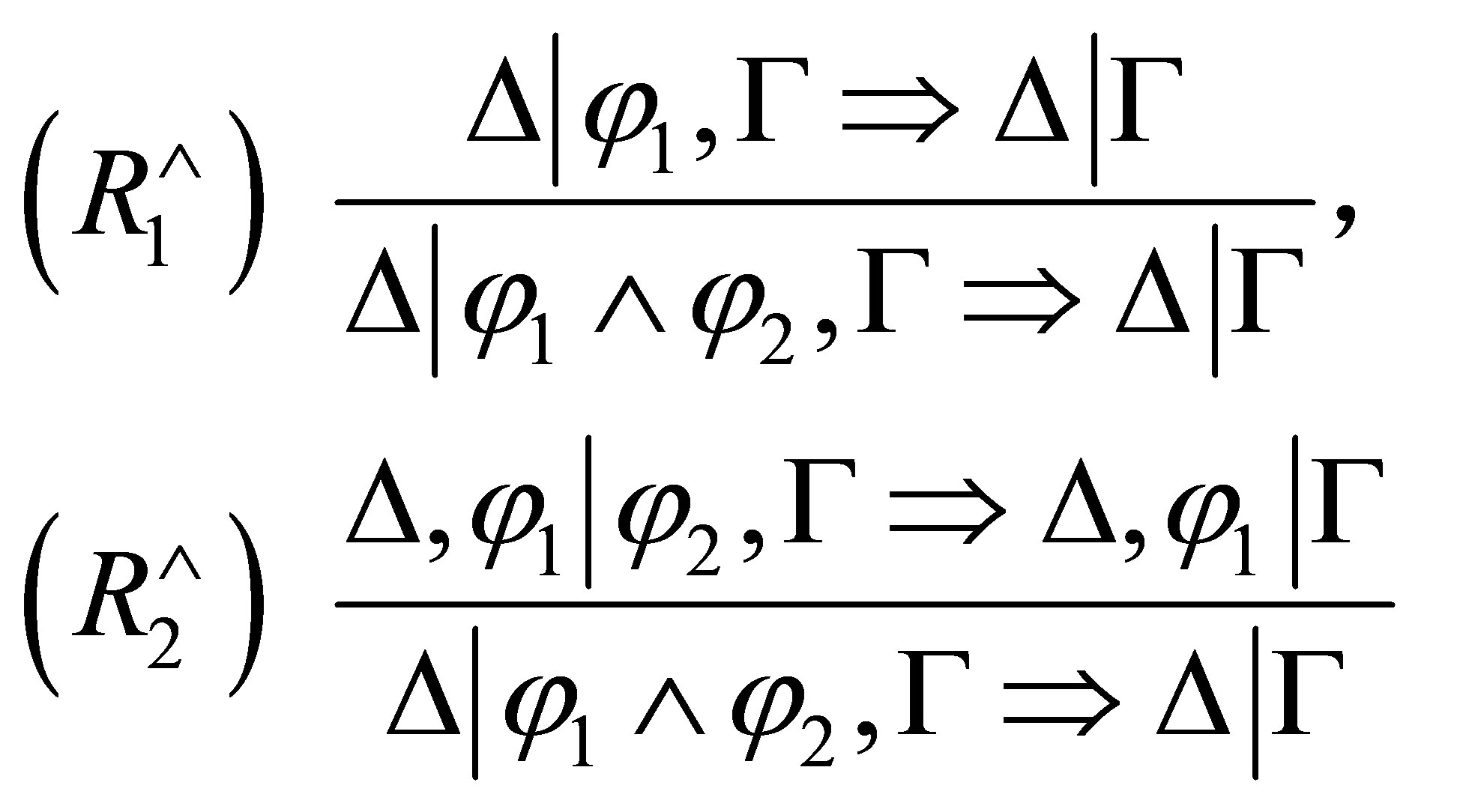
in 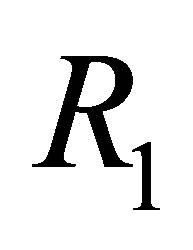 and
and 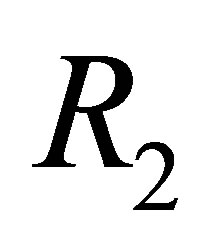 instead of
instead of
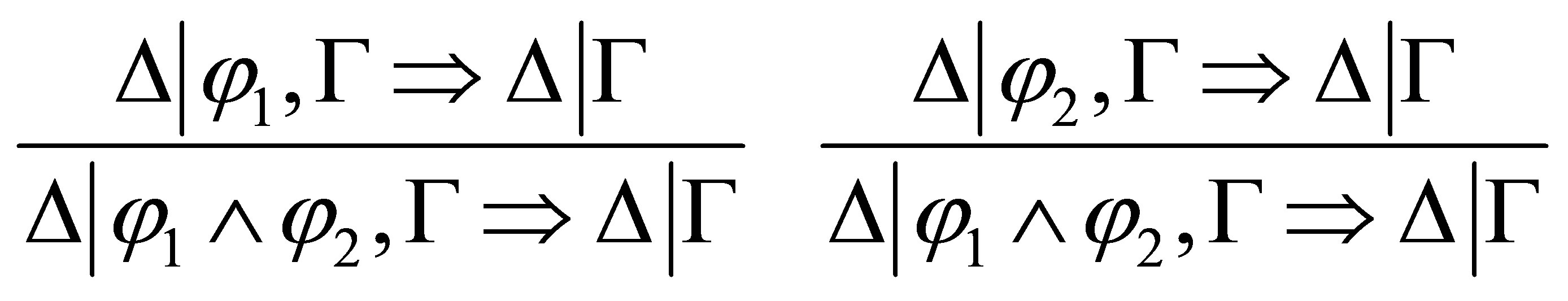
in the 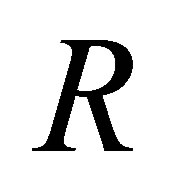 -calculus.
-calculus.
In 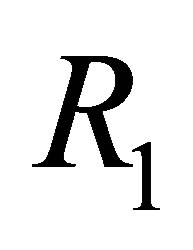 we use a rule
we use a rule
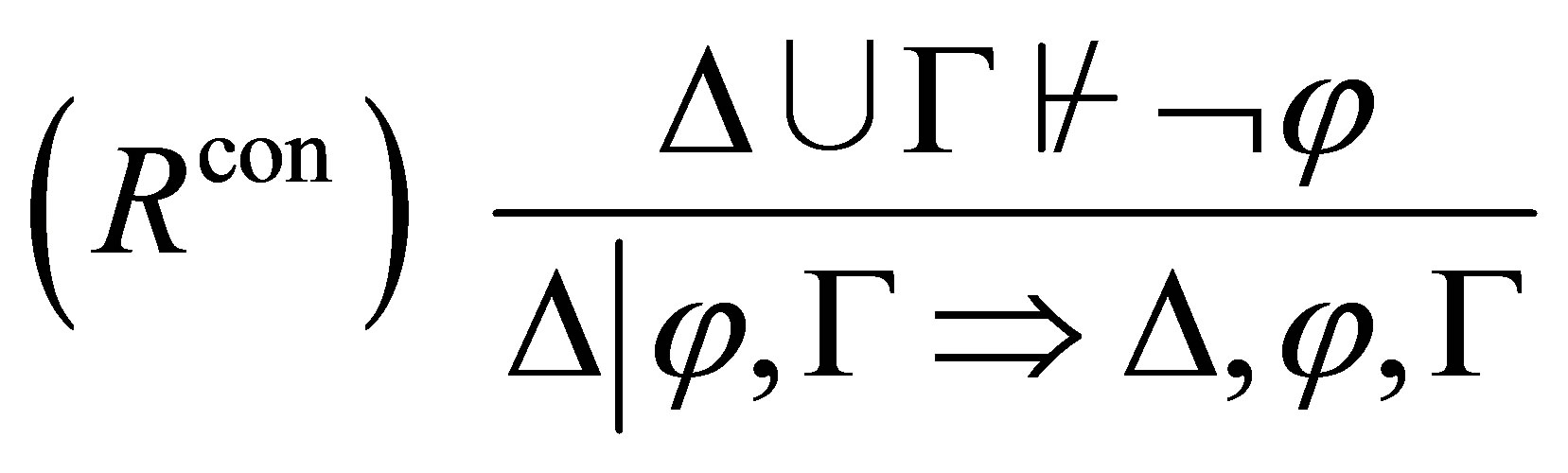
to deduce 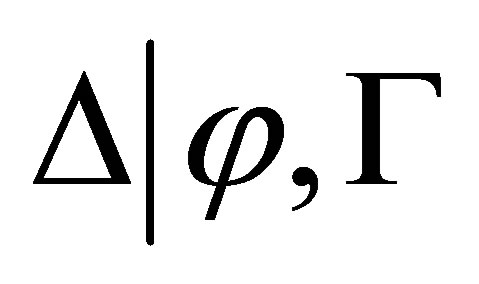 to
to 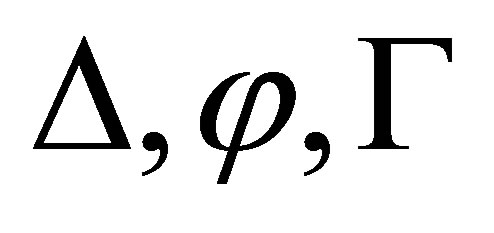 if
if 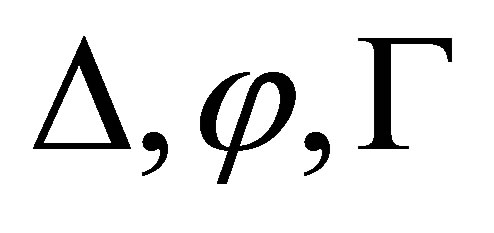 are consistent. In
are consistent. In , we shall give a deduction rule to reduce
, we shall give a deduction rule to reduce  to the atomic cases where
to the atomic cases where
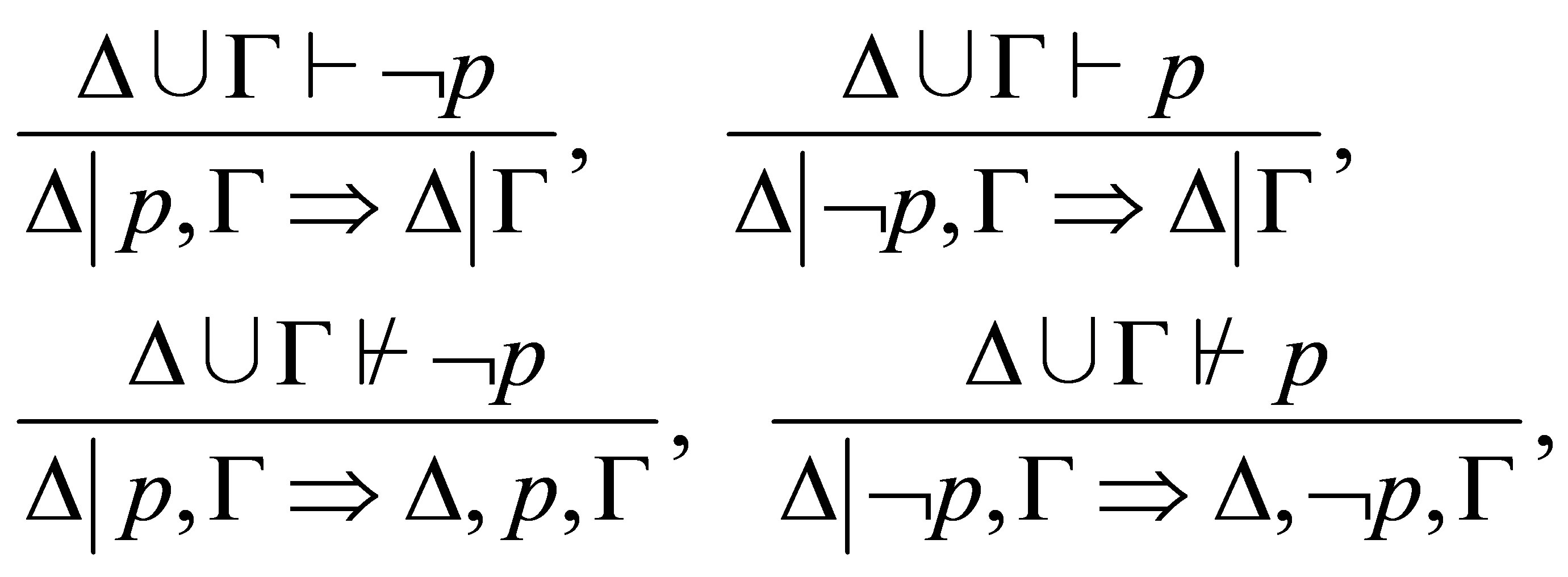
with a cost that we cannot prove that if 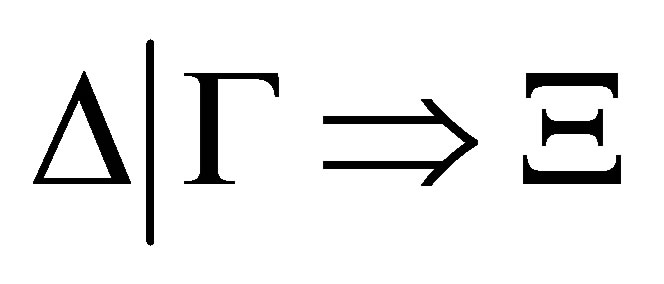 is provable then
is provable then  is a pseudo-revision of
is a pseudo-revision of  by
by  Instead we shall prove that if
Instead we shall prove that if  is provable then
is provable then  is a pre-revision of
is a pre-revision of  by
by  that is, there is a consistent theory
that is, there is a consistent theory 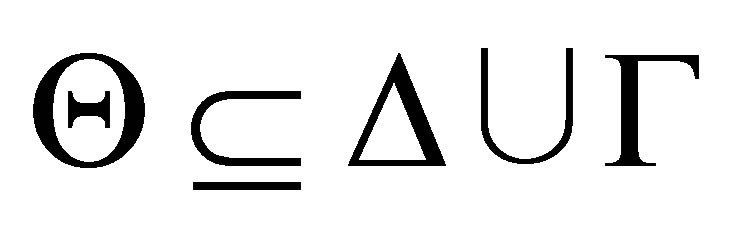 such that 1)
such that 1) 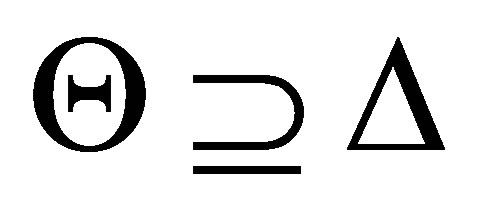 is a pseudo-revision of
is a pseudo-revision of 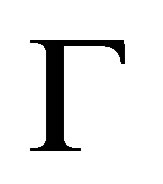 by
by  2)
2) 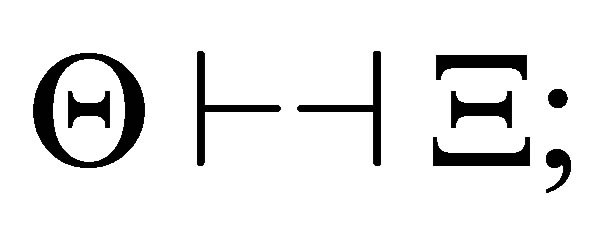 and 3) no subformula
and 3) no subformula  of
of  is contradictory to
is contradictory to 
The paper is organized as follows: the next section gives the  -calculus in [3] and basic definitions; the third section defines an
-calculus in [3] and basic definitions; the third section defines an 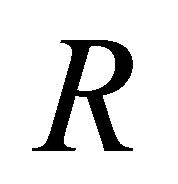 -calculus
-calculus 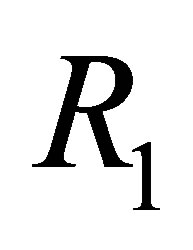 for the pseudorevision and proves that
for the pseudorevision and proves that 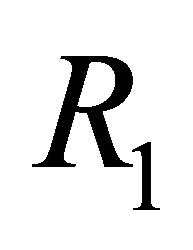 is sound and complete with respect to the pseudo-revision; the fourth section defines another
is sound and complete with respect to the pseudo-revision; the fourth section defines another  -calculus
-calculus 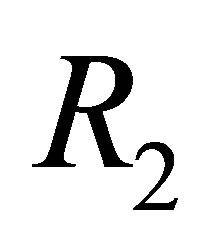 for the pre-revision and prove that
for the pre-revision and prove that  is sound and complete with respect to the pseudo-revision, and the last section concludes the whole paper.
is sound and complete with respect to the pseudo-revision, and the last section concludes the whole paper.
2. The  -Calculus
-Calculus
The 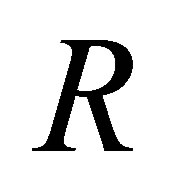 -calculus is defined on a first-order logical language. Let
-calculus is defined on a first-order logical language. Let  be a logical language of the first-order logic;
be a logical language of the first-order logic;  formulas and
formulas and 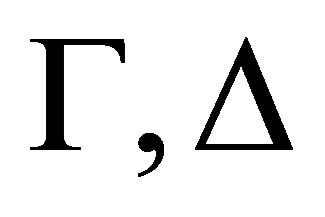 sets of formulas (theories), where
sets of formulas (theories), where  is a set of atomic formulas or the negations of atomic formulas, and
is a set of atomic formulas or the negations of atomic formulas, and  is called an R-configuration.
is called an R-configuration.
The  -calculus consists of the following axiom and inference rules:
-calculus consists of the following axiom and inference rules:
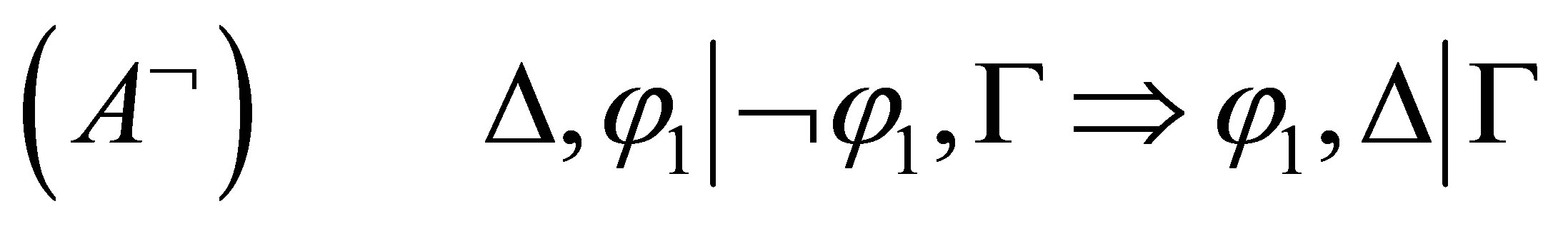
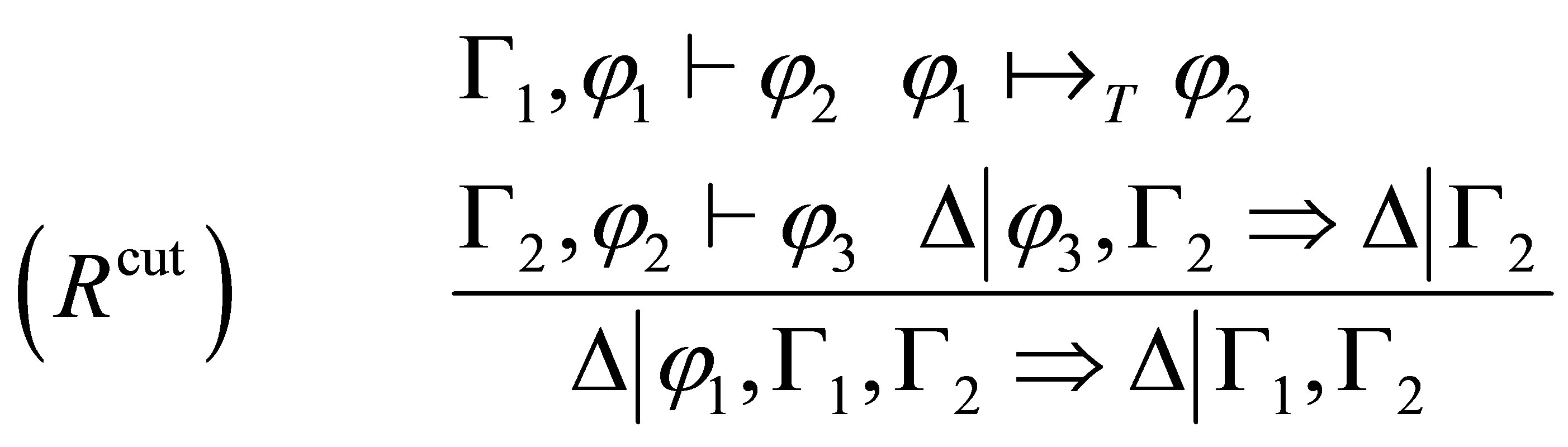
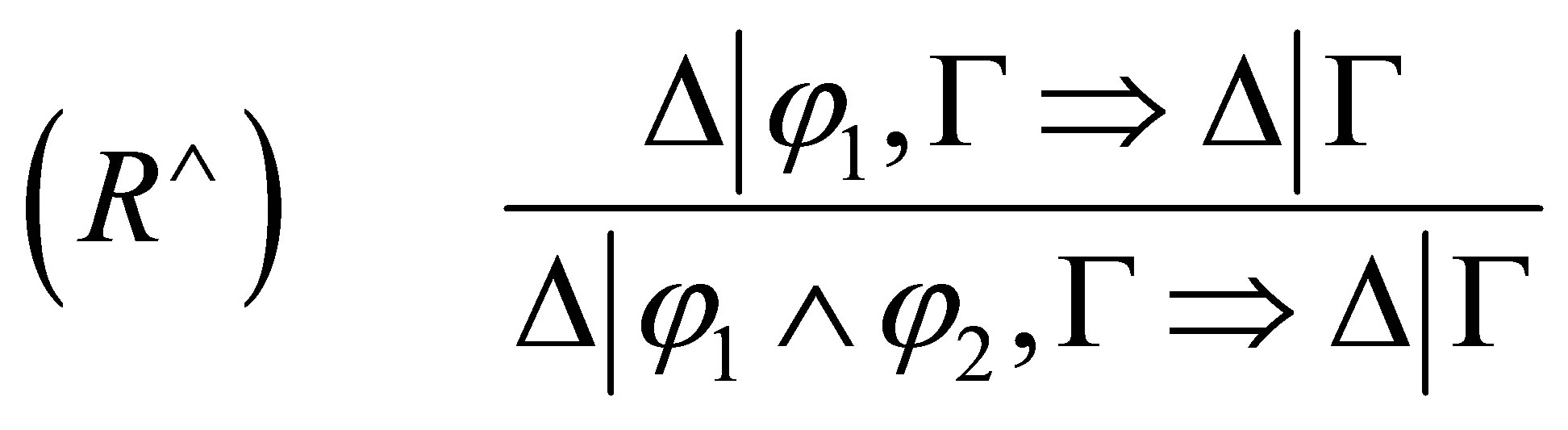
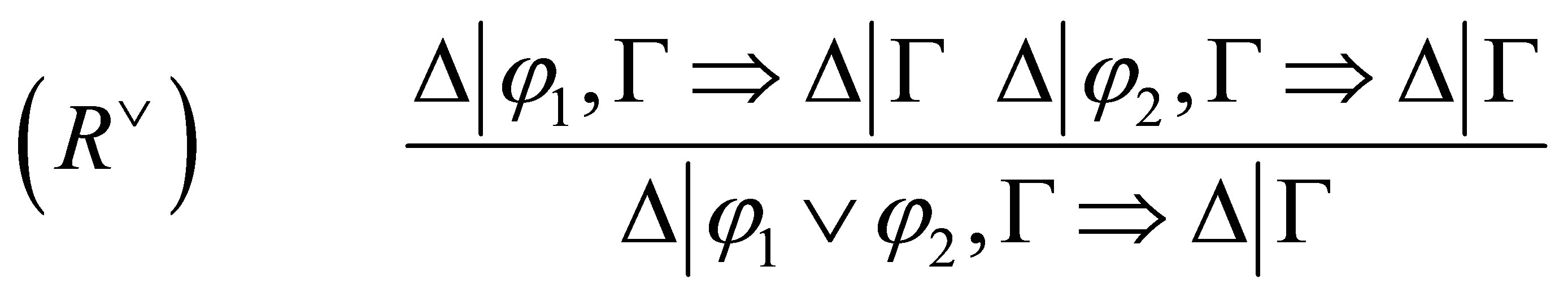

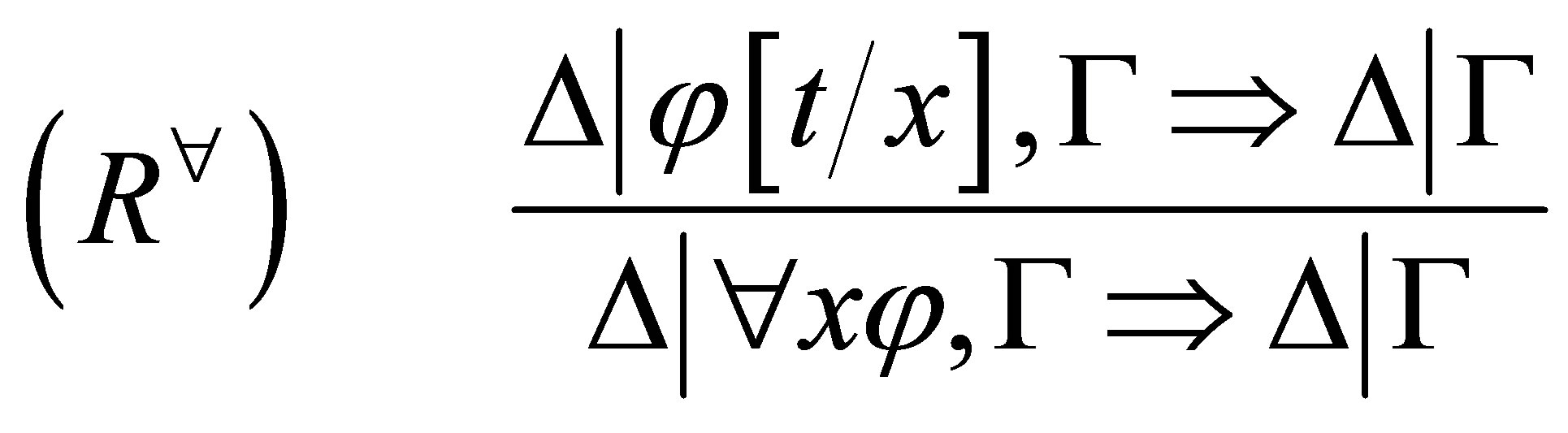
where in 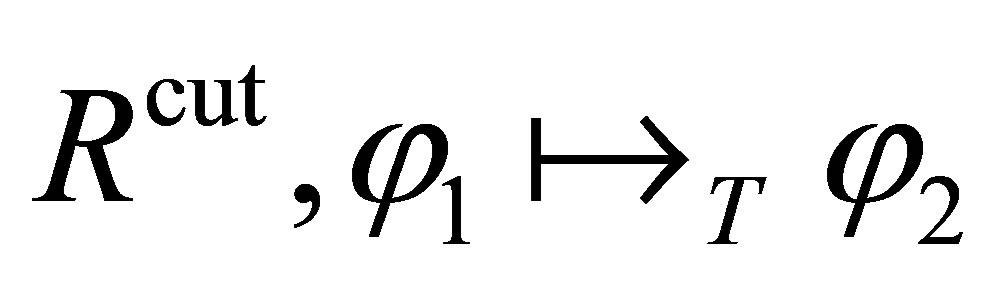 means that
means that  occurs in the proof tree
occurs in the proof tree  of
of 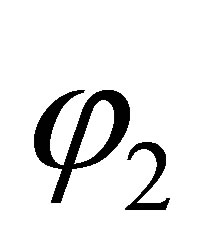 from
from 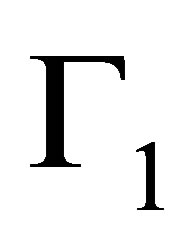 and
and 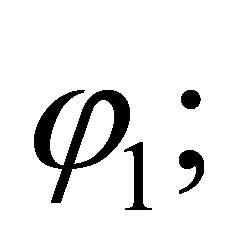 and in
and in 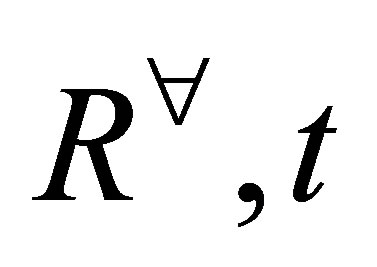 is a term, and is free in
is a term, and is free in  for
for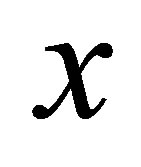 .
.
The  -calculus is in the first-order logic. In the following we discuss the
-calculus is in the first-order logic. In the following we discuss the  -calculi in the propositional logic.
-calculi in the propositional logic.
Let  be a logical language of the propositional logic which contains the following symbols:
be a logical language of the propositional logic which contains the following symbols:
Ÿ propositional variables: 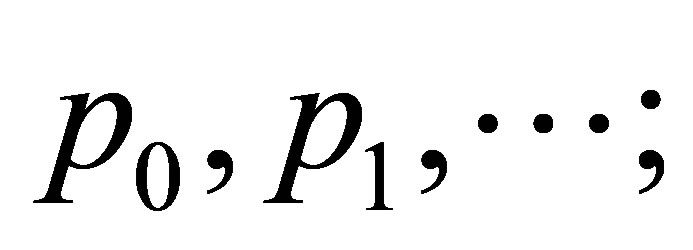
Ÿ logical connectives: 
Formulas are defined as follows:
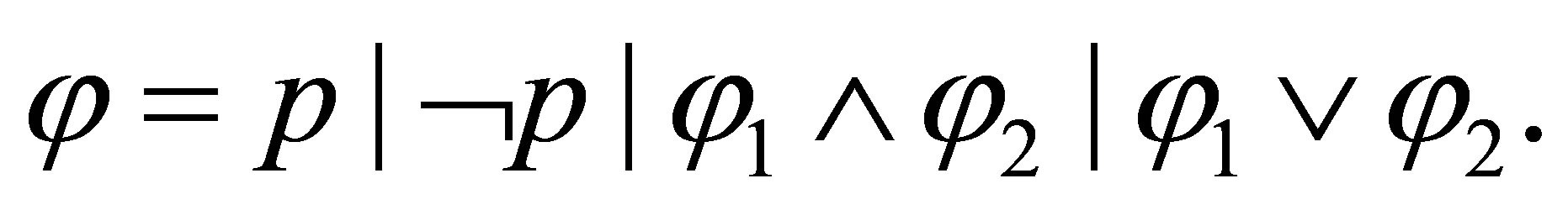
Definition 2.1. Given a consistent set  of formulas and a finite consistent set
of formulas and a finite consistent set  of formulas, a consistent set
of formulas, a consistent set  of formulas is a pseudo-revision of
of formulas is a pseudo-revision of  by
by  if
if 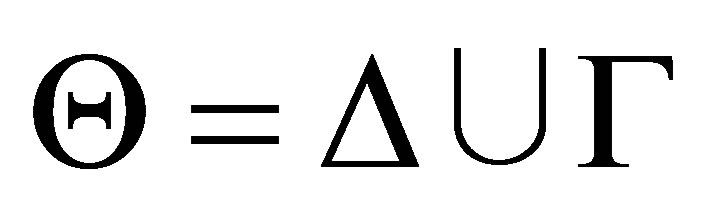 (if
(if 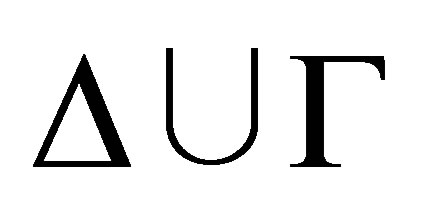 is consistent), or (if
is consistent), or (if 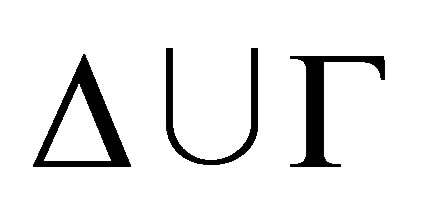 is inconsistent then)
is inconsistent then)  satisfies the following conditions:
satisfies the following conditions:
1) 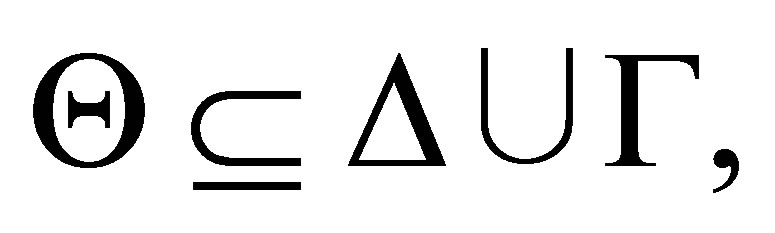
2)  and 3) there is a
and 3) there is a 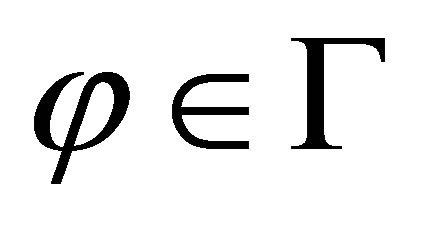 such that
such that 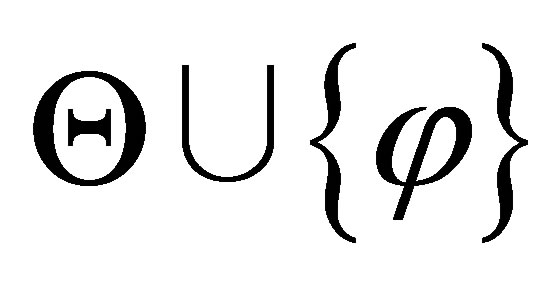 is inconsistent.
is inconsistent.
Each pseudo-revision  can be generated by the following procedure: given any consistent set
can be generated by the following procedure: given any consistent set  and finite consistent set
and finite consistent set 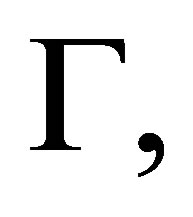 assume that
assume that 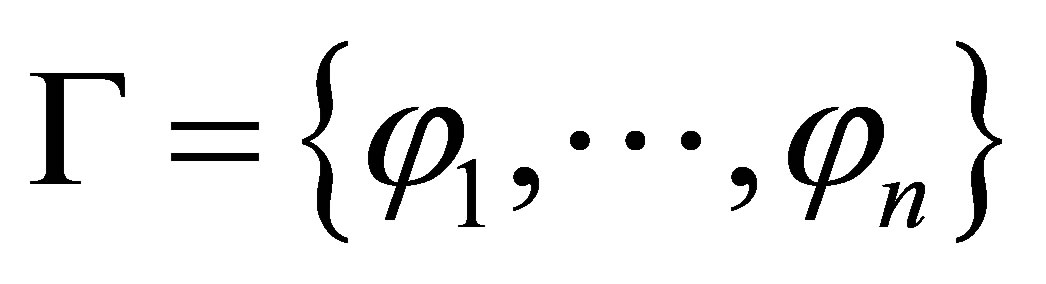 is ordered by a linear ordering
is ordered by a linear ordering  (without loss of generality, assume that
(without loss of generality, assume that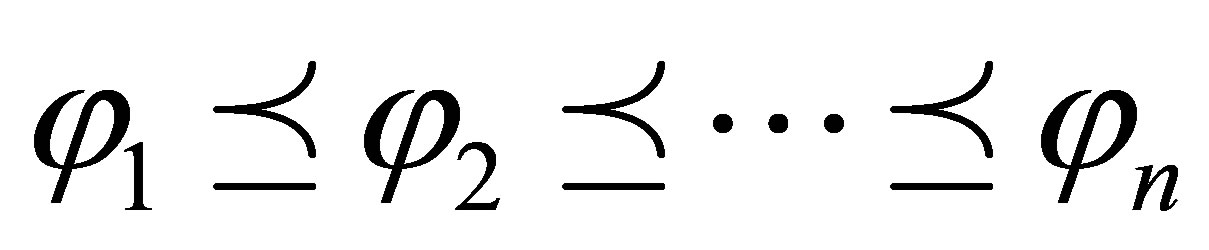 ), define
), define

Let 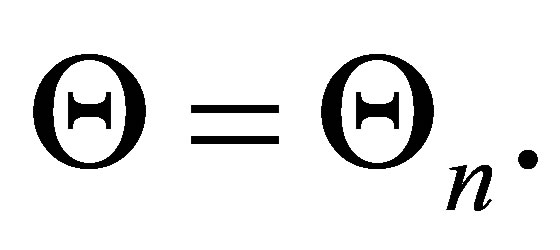 Then,
Then,  is a subset of
is a subset of 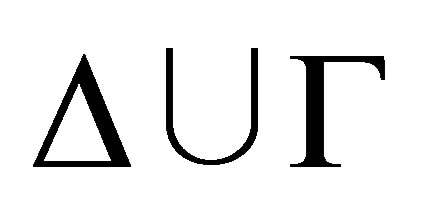 such that
such that  and
and  is consistent.
is consistent.
Lemma 2.2.  is a pseudo-revision of
is a pseudo-revision of 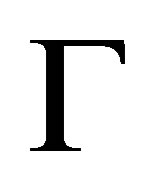 by
by  Moreover, Let
Moreover, Let 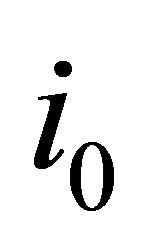 be the least
be the least  such that
such that
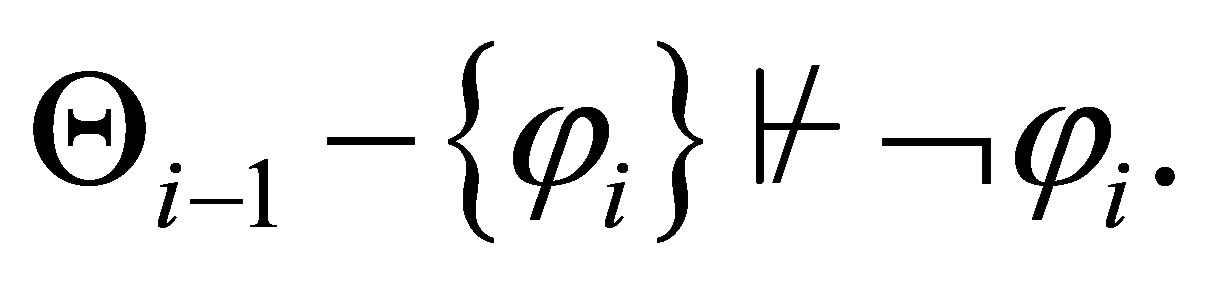 Then,
Then, 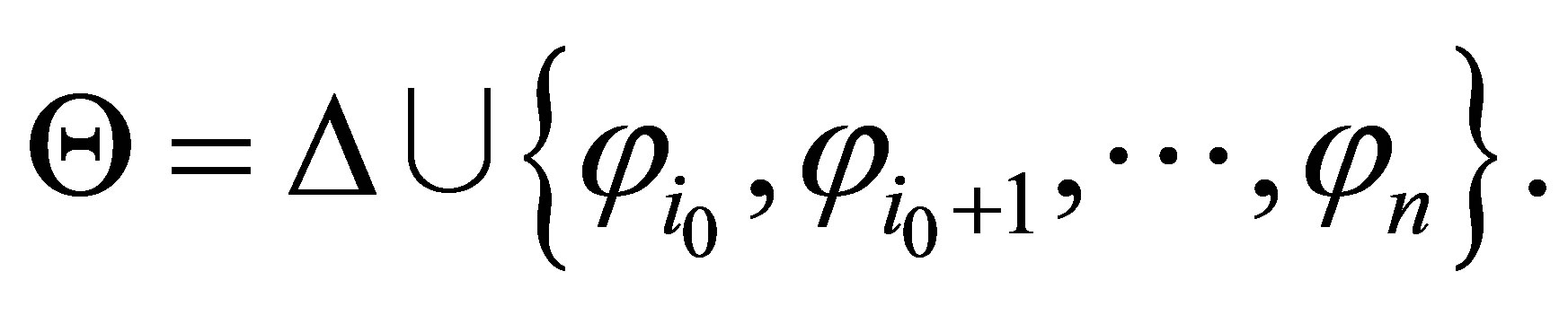
Definition 2.3. Given a consistent set  of formulas and a finite consistent set
of formulas and a finite consistent set 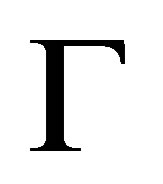 of formulas, a consistent set
of formulas, a consistent set  of formulas is a pre-revision of
of formulas is a pre-revision of 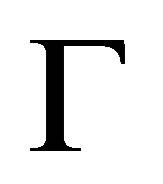 by
by  if there is a pseudo-revision
if there is a pseudo-revision  of
of  by
by  such that 1)
such that 1) 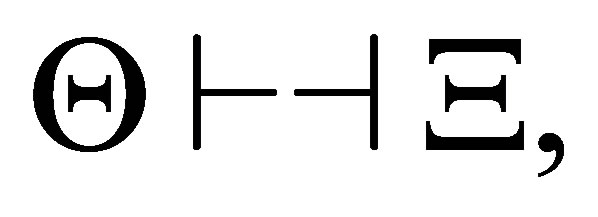
2) 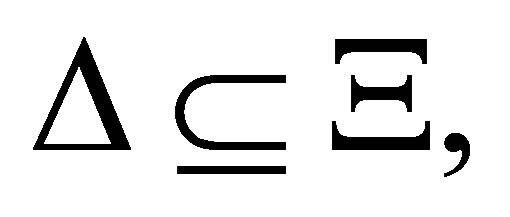 and 3) no subformula
and 3) no subformula  of
of  is contradictory to
is contradictory to 
Each pre-revision  can be generated by the following procedure: given any consistent set
can be generated by the following procedure: given any consistent set  and finite consistent set
and finite consistent set  assume that
assume that 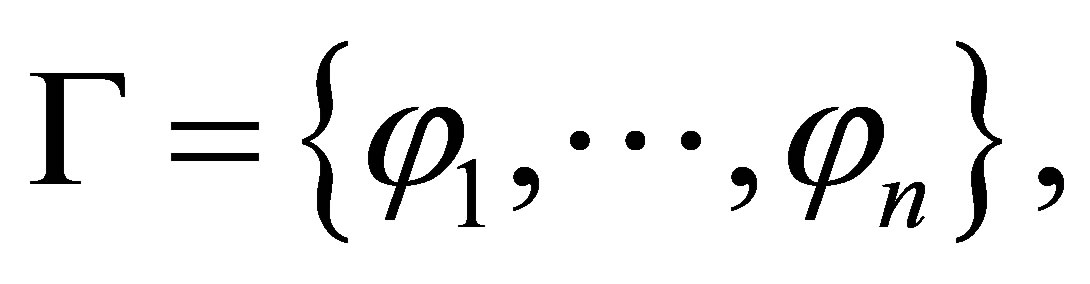 define
define
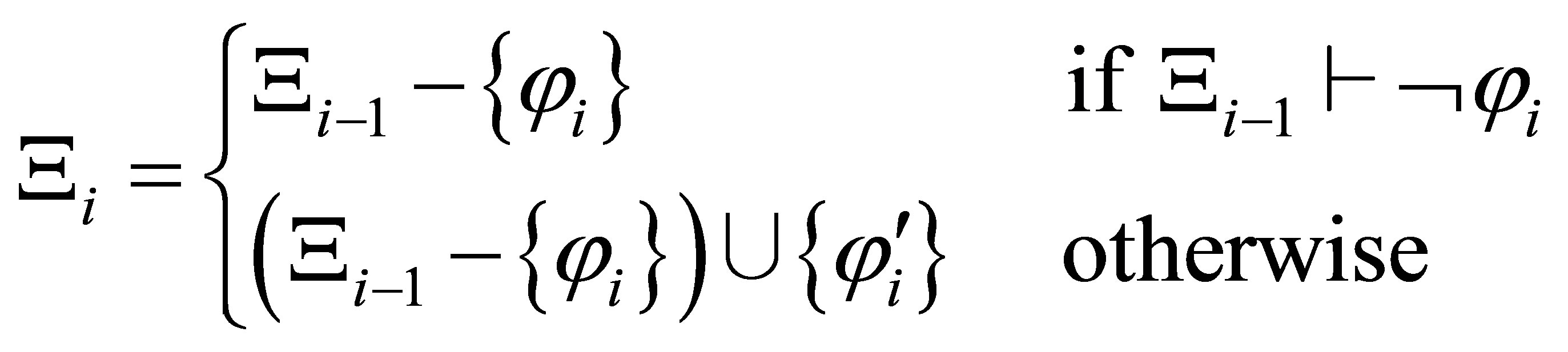
where
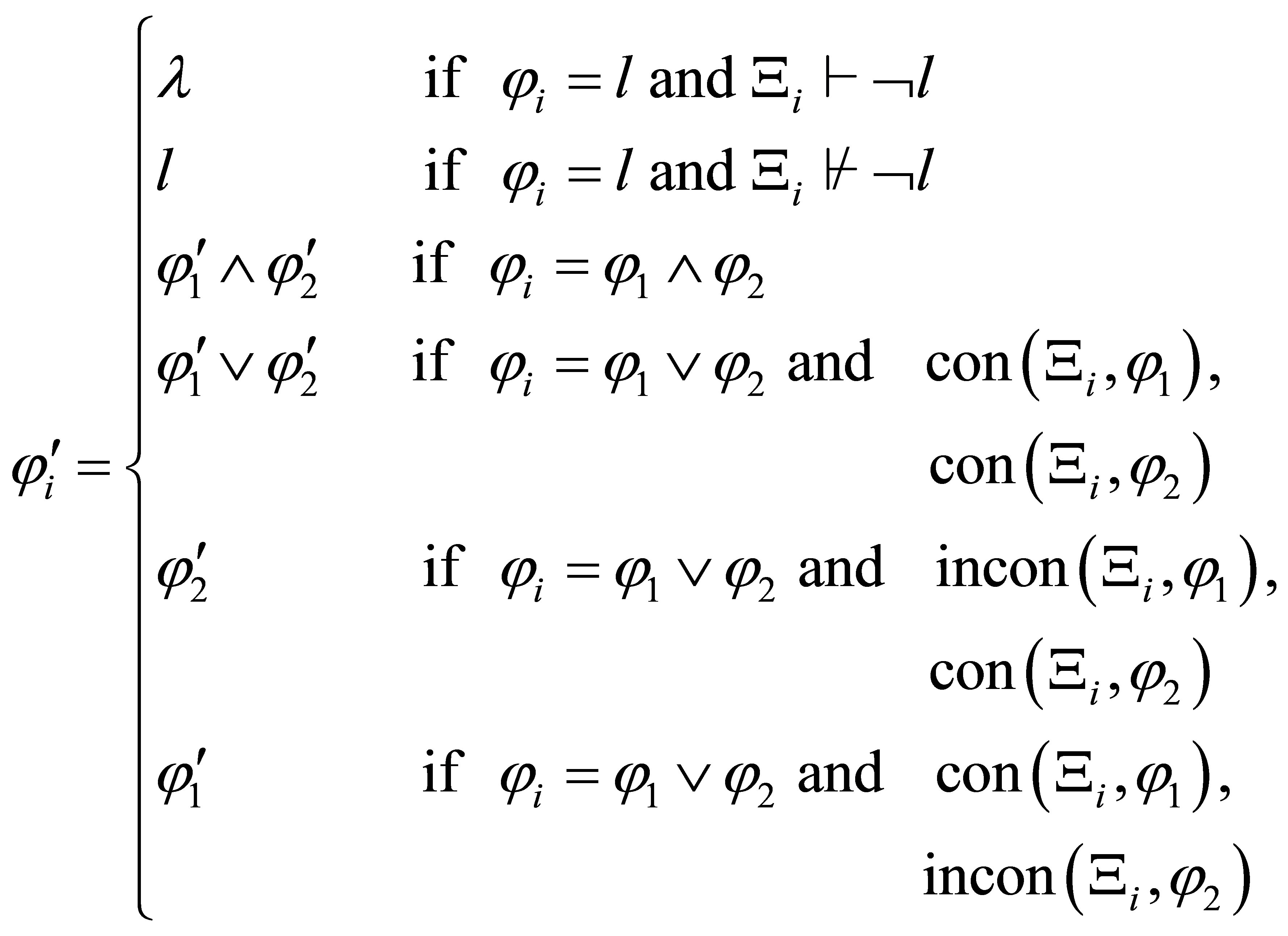
where 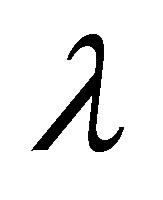 is the empty string.
is the empty string.
Let  and
and  be the pseudo-revision of
be the pseudo-revision of  by
by  in the same ordering as
in the same ordering as  Then, we have the following Lemma 2.4. Let
Then, we have the following Lemma 2.4. Let 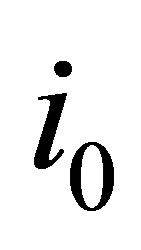 be the least
be the least  such that
such that 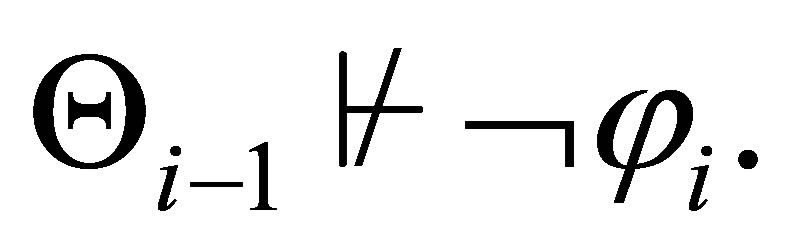 Then, for any
Then, for any  and for any
and for any 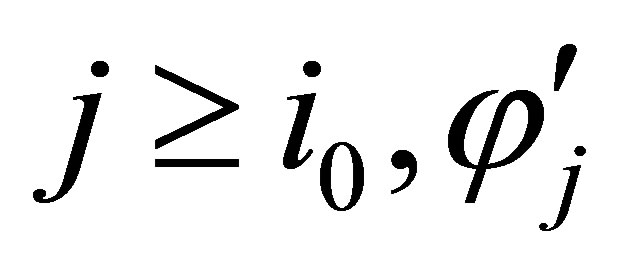 is a subformula of
is a subformula of 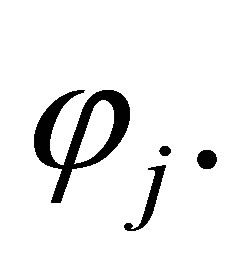
Lemma 2.5.  is a pre-revision of
is a pre-revision of 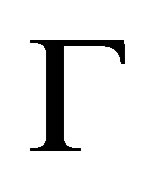 by
by  such that
such that 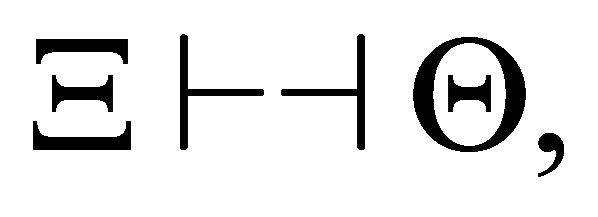 and no subformula of
and no subformula of  is contradictory to
is contradictory to 
Proof. Let 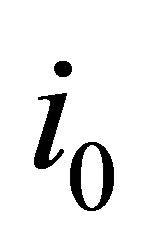 be the least
be the least  such that
such that 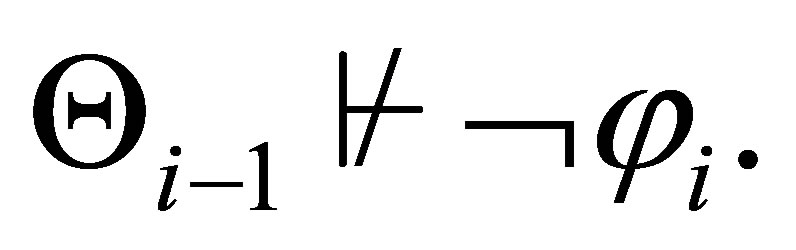 Then,
Then,
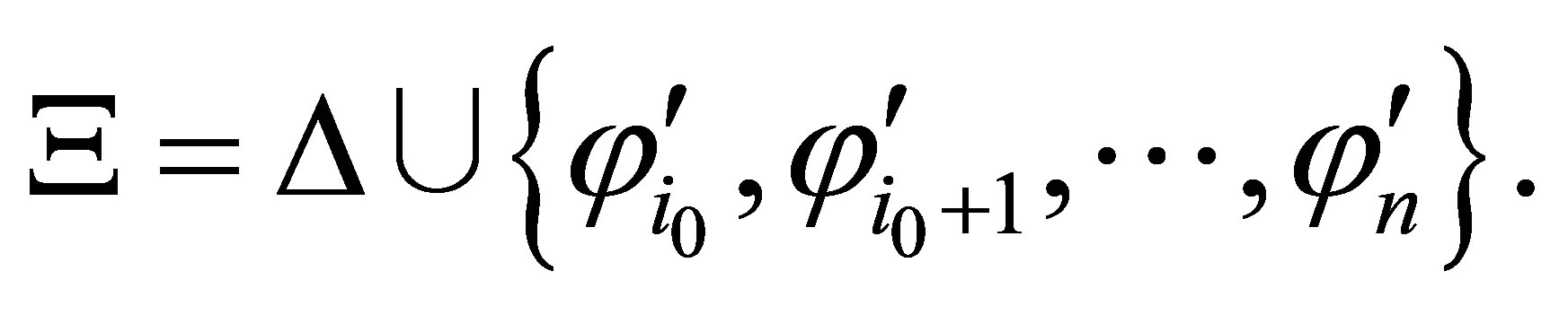
We prove that for any  with
with 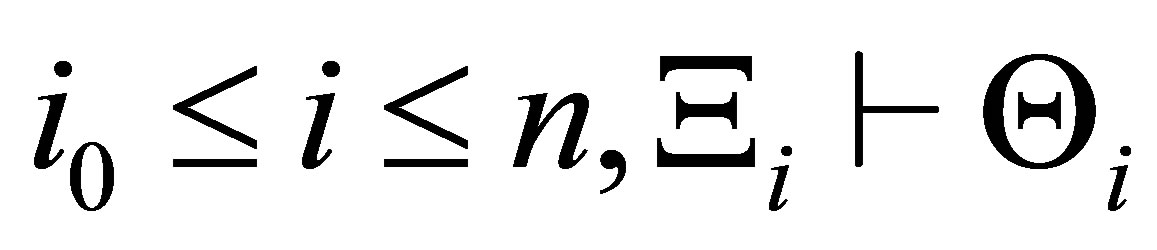 and
and  by induction on
by induction on 
Let 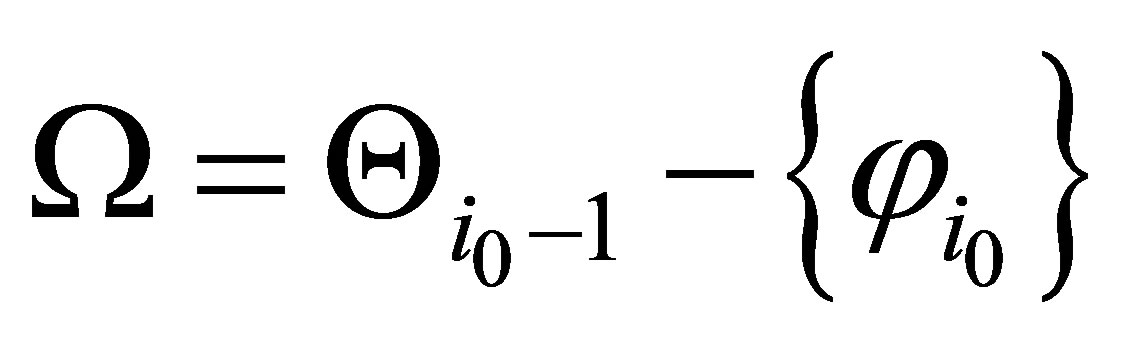 and
and 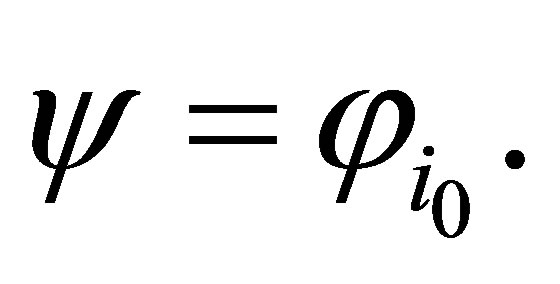 Then,
Then,
 We prove by induction on the structure of
We prove by induction on the structure of 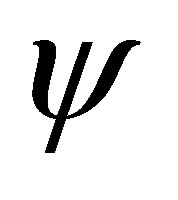 that
that 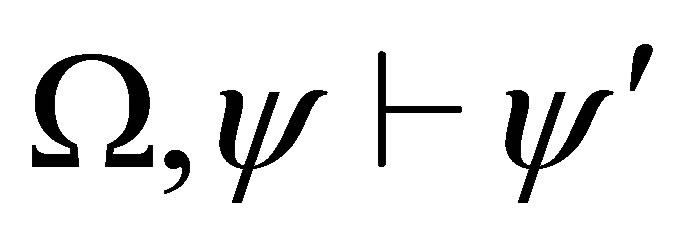 and
and 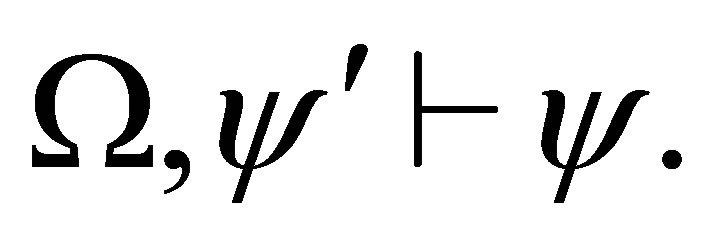
If  and
and 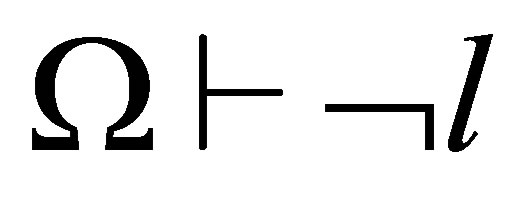 then
then  is inconsistent, a contradiction to the choice of
is inconsistent, a contradiction to the choice of 
If 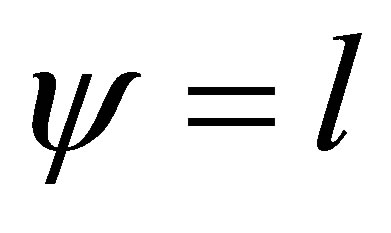 and
and 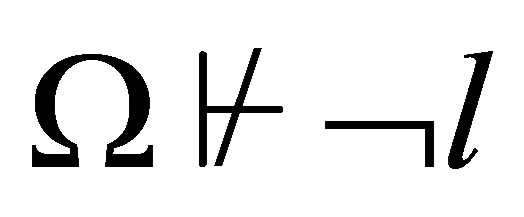 then
then 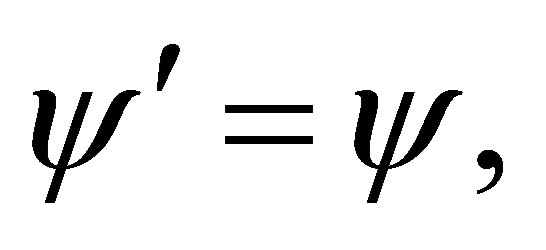 and
and 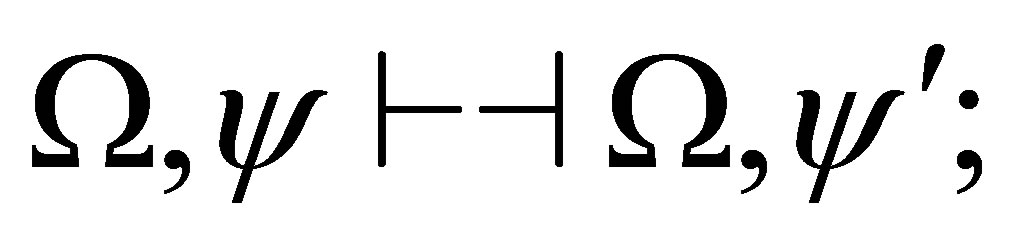
If  and
and 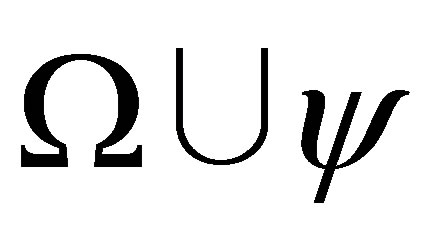 is consistent then
is consistent then  and
and 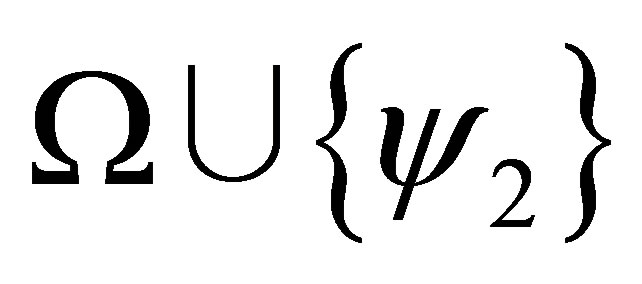 are consistent, and by the induction assumption,
are consistent, and by the induction assumption,

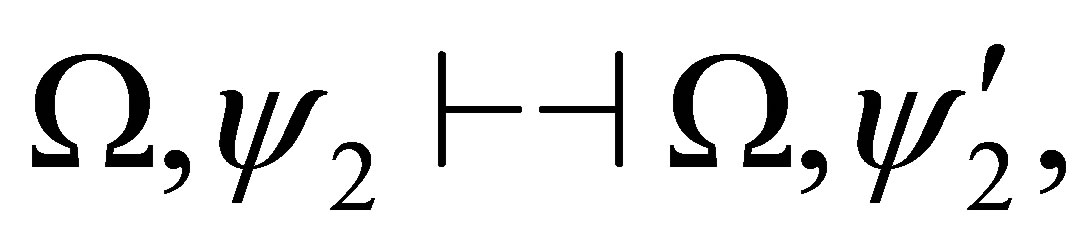
and hence,
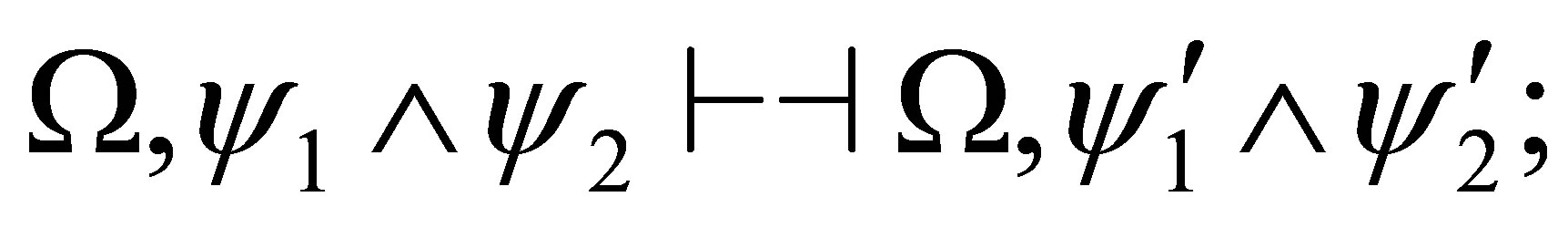
If 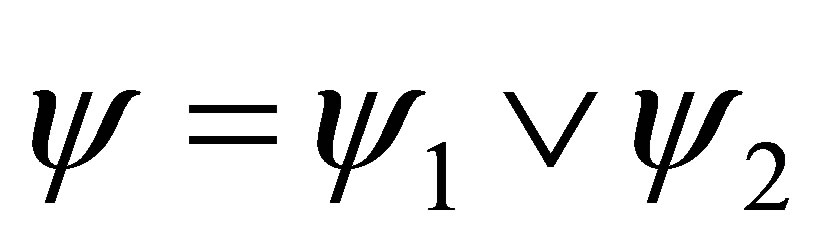 and
and 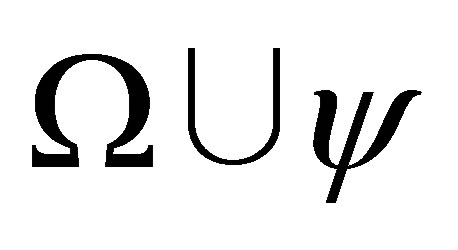 is consistent then either
is consistent then either  or
or 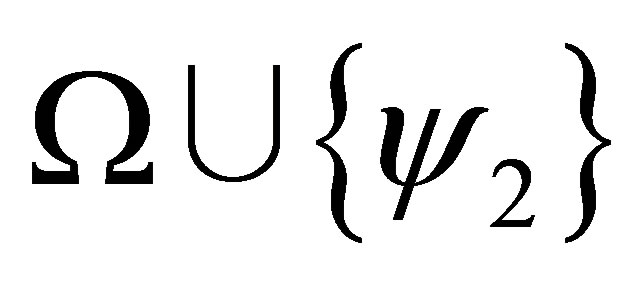 is consistent.
is consistent.
If 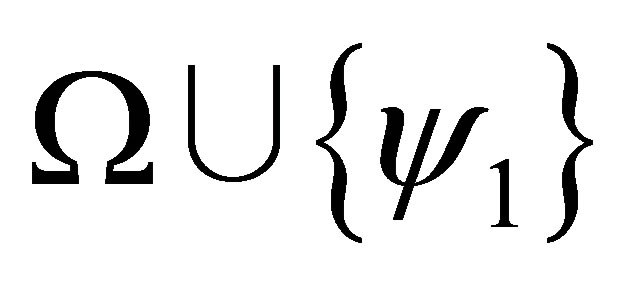 and
and 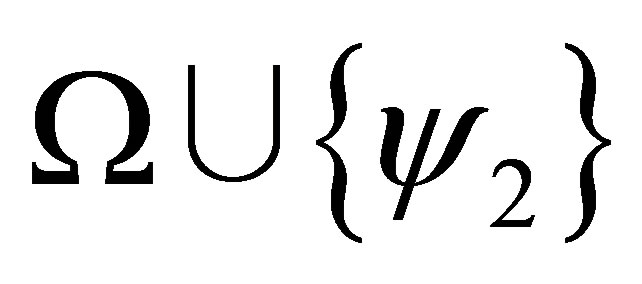 are consistent. then by the induction assumption,
are consistent. then by the induction assumption,
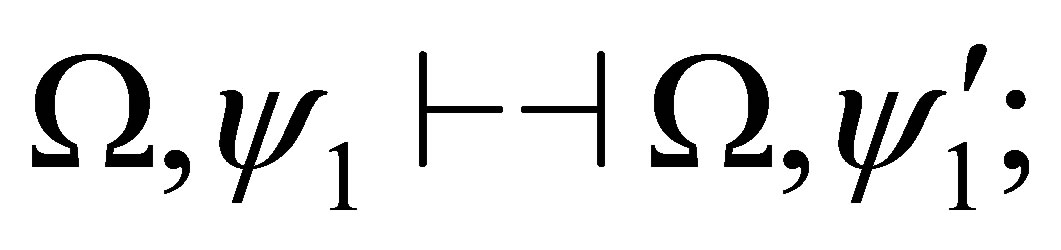
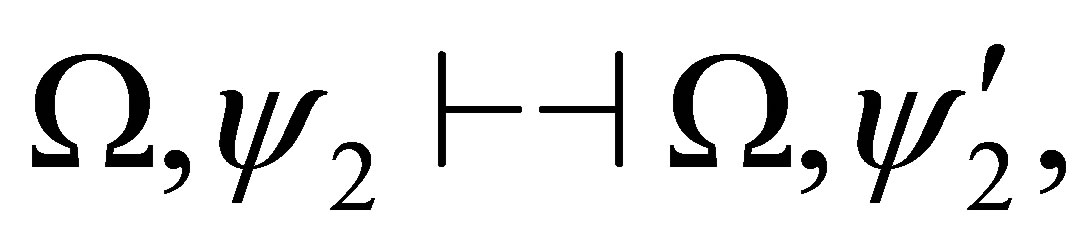
and hence, 
If 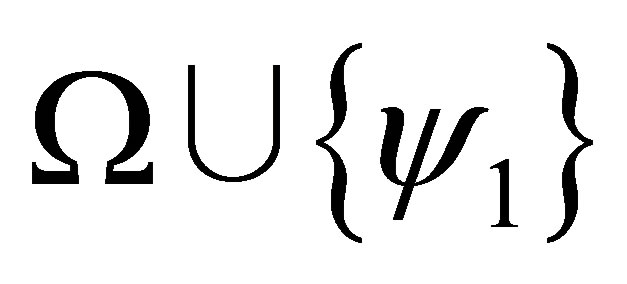 is inconsistent and
is inconsistent and 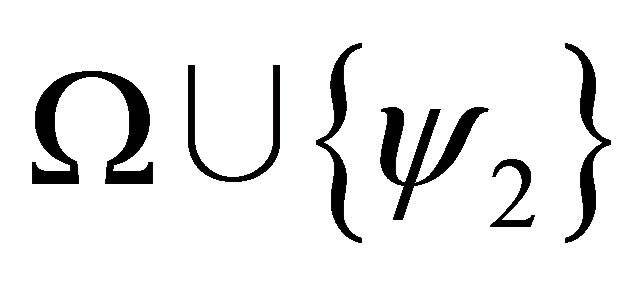 is consistent. then
is consistent. then  and by the induction assumption,
and by the induction assumption, 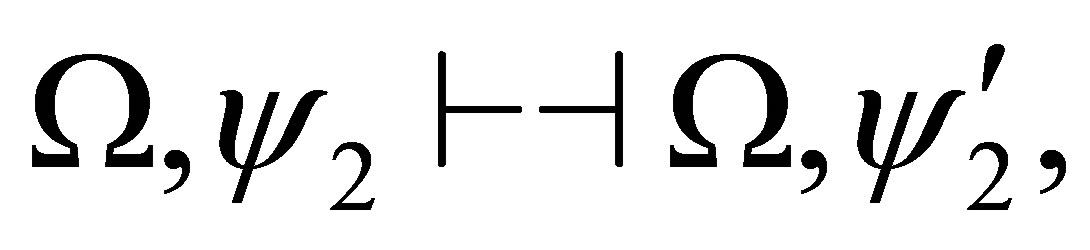 and hence,
and hence, 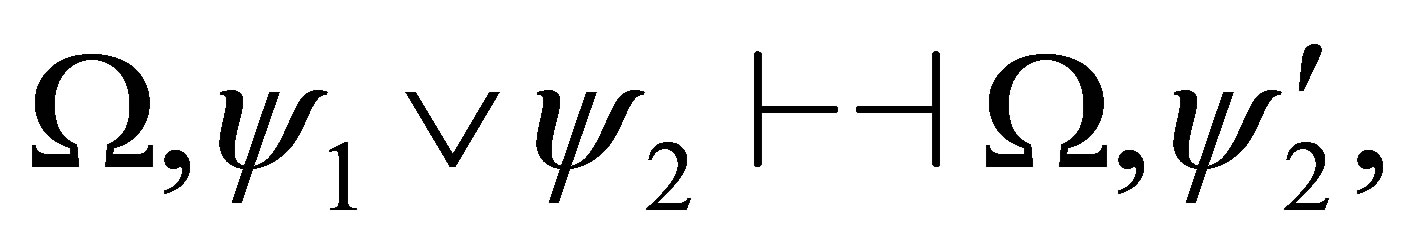 because
because  and
and 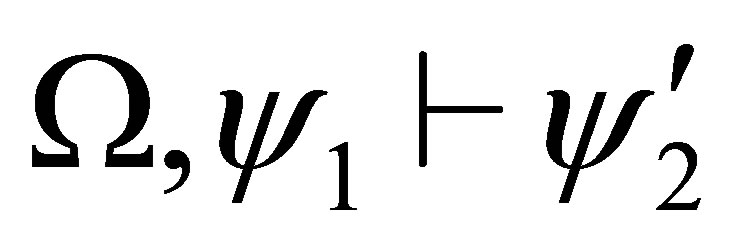 (
(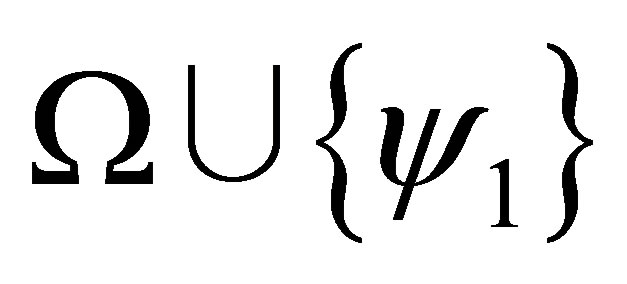 is inconsistent, and hence, for any formula
is inconsistent, and hence, for any formula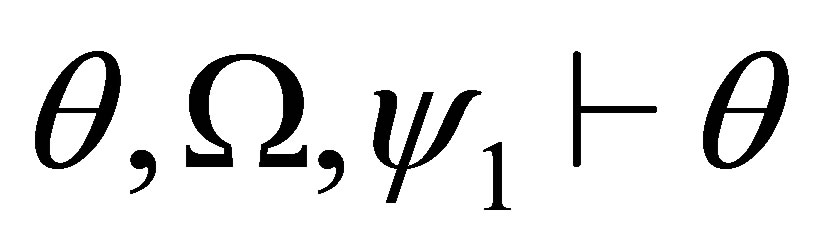 ).
).
Similar for the case that 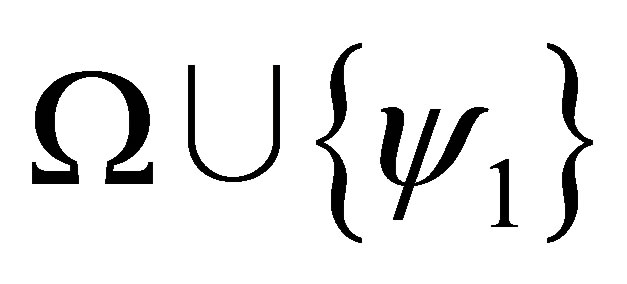 is consistent and
is consistent and 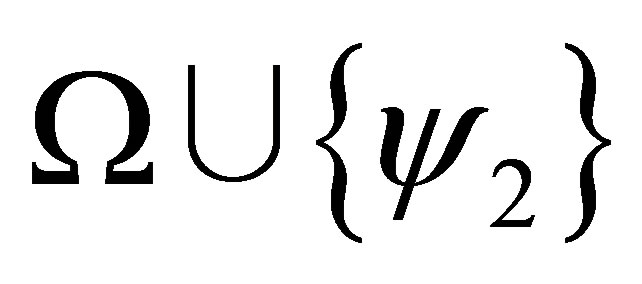 is inconsistent.
is inconsistent.
Similarly we can prove that for any  with
with 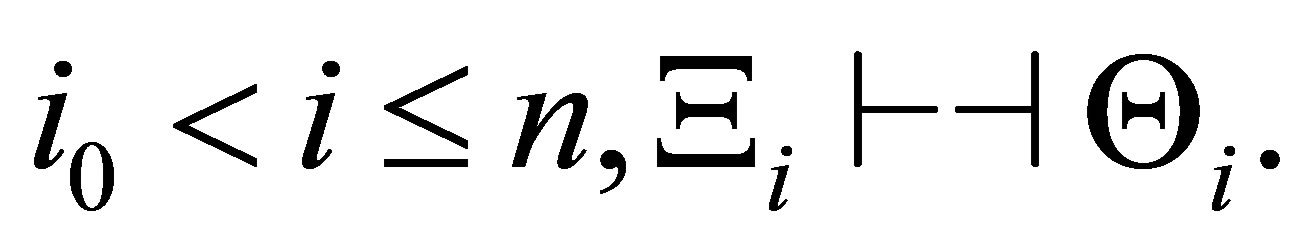
3. The  -Calculus
-Calculus 
In this section we give an 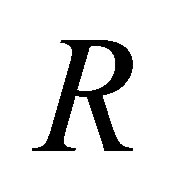 -calculus
-calculus  which is sound and complete with respect to the pseudo-revision, where the decision of whether
which is sound and complete with respect to the pseudo-revision, where the decision of whether  is consistent is needed so that if
is consistent is needed so that if  is consistent then
is consistent then 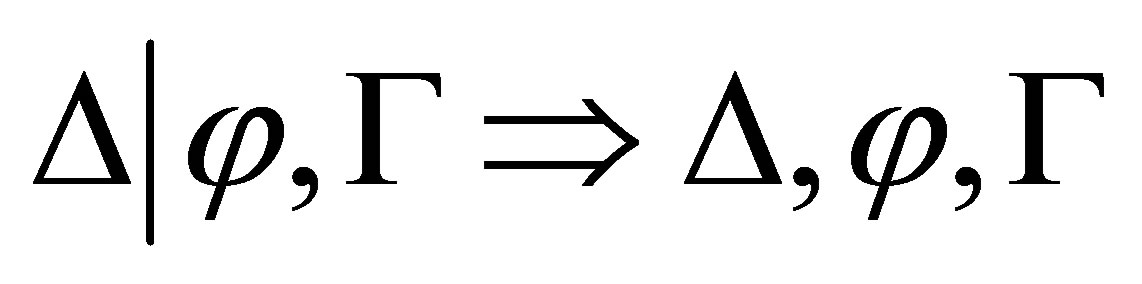 is provable; otherwise,
is provable; otherwise, 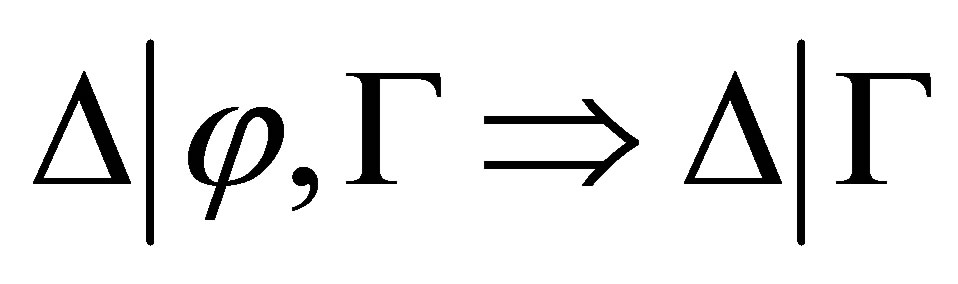 is provable.
is provable.
Let 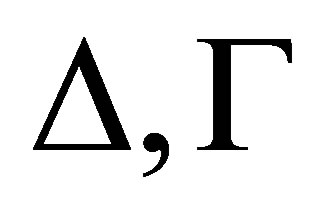 be any consistent sets of formulas.
be any consistent sets of formulas.
Definition 3.1. 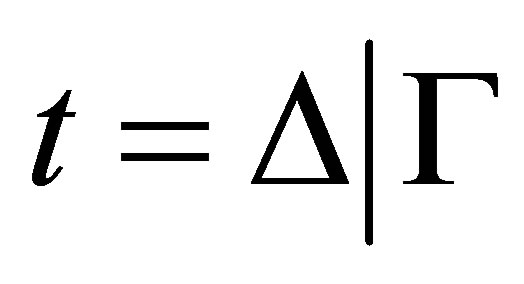 is a term; and
is a term; and  is a statement, where
is a statement, where 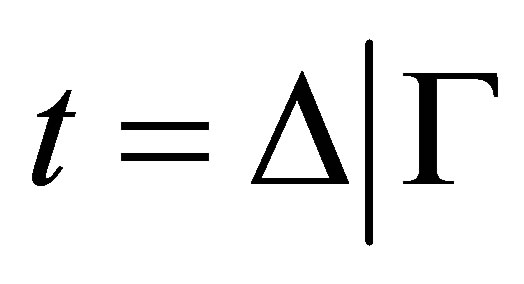 and
and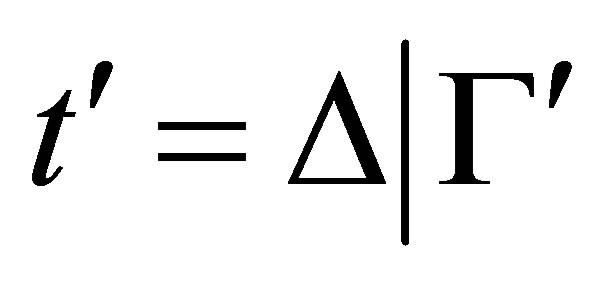 ; and
; and 
is a deduction rule, where 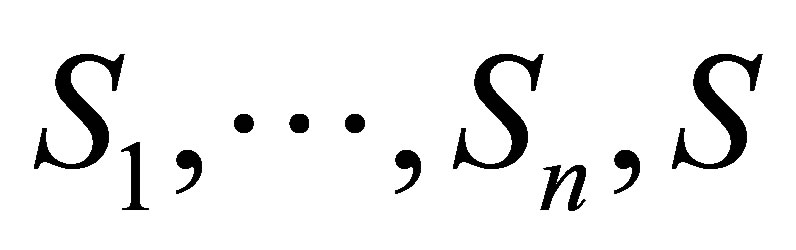 are statements.
are statements.
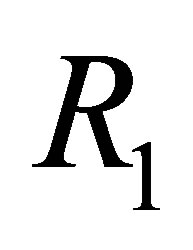 has the following deduction rules:
has the following deduction rules:
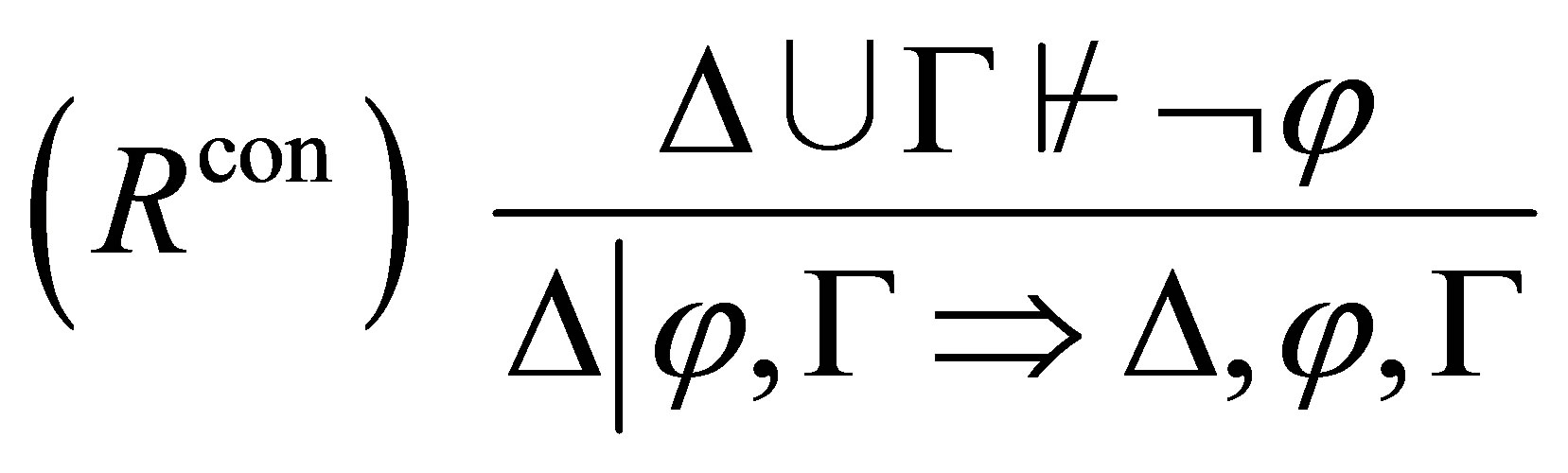
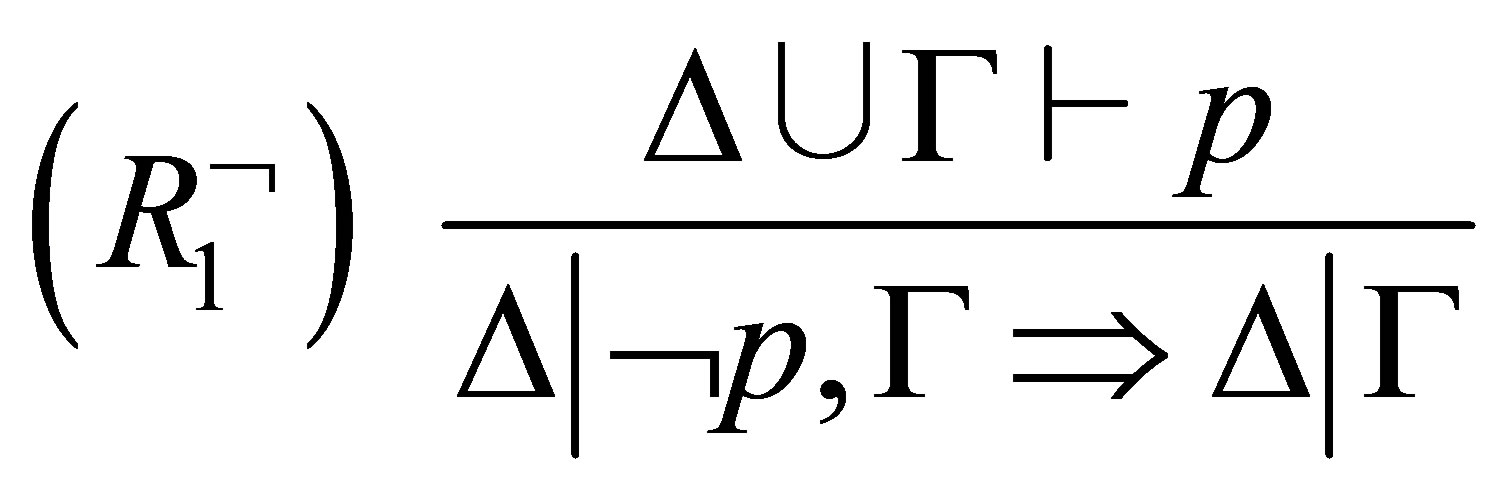
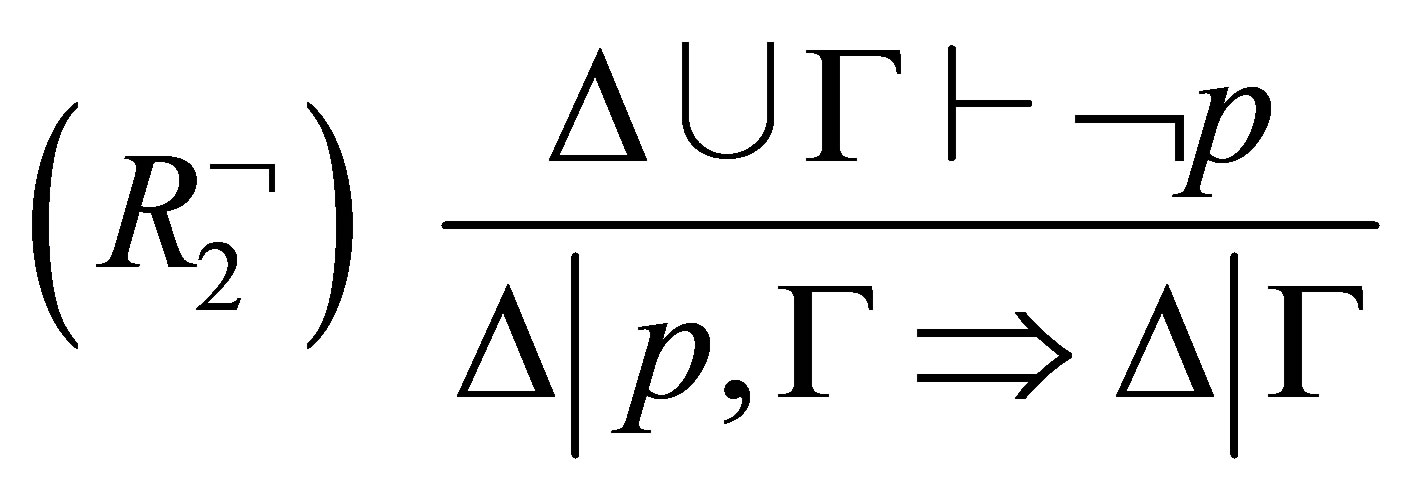
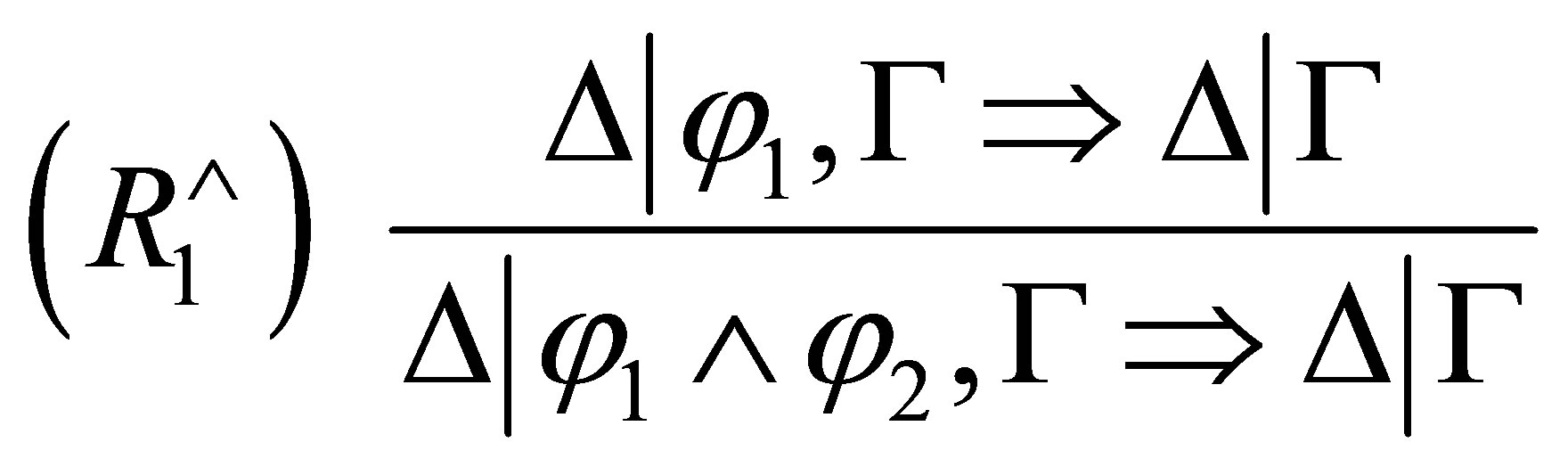

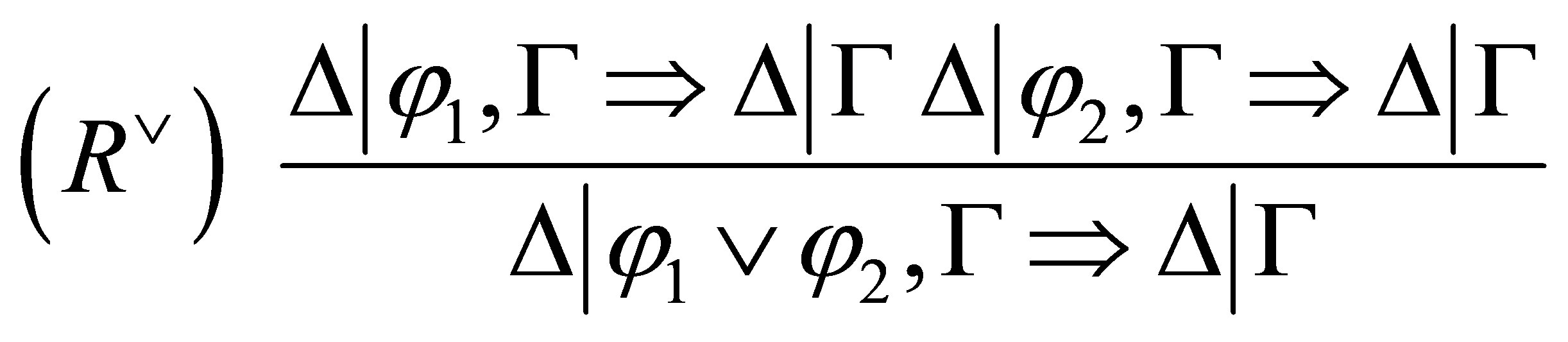
Definition 3.2. 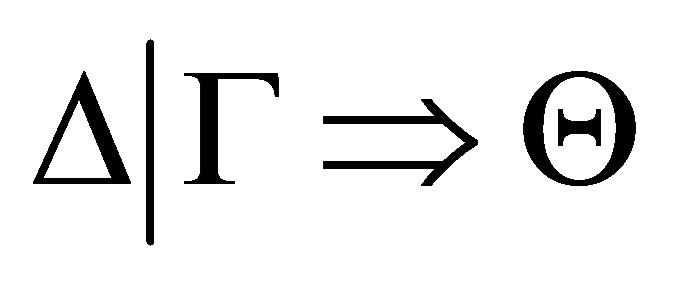 is provable if there is a sequence
is provable if there is a sequence
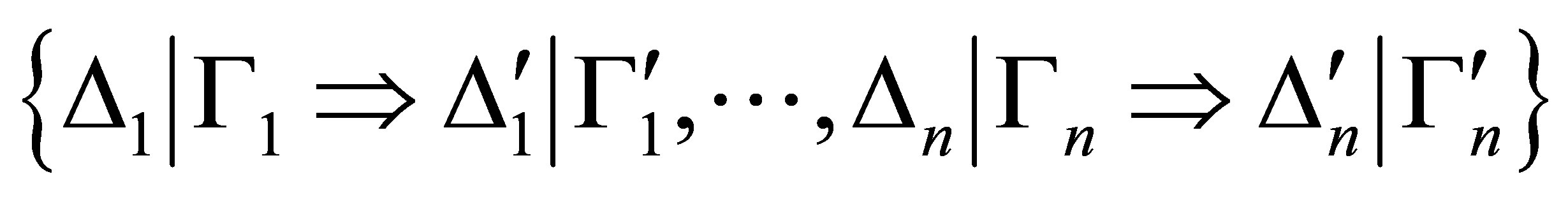
of statements such that 1) 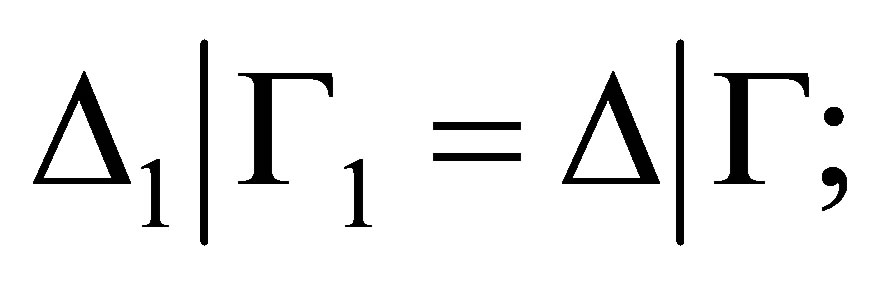
2) 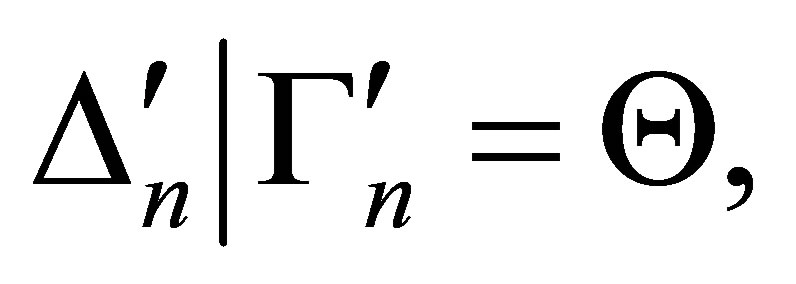 and 3) for each
and 3) for each 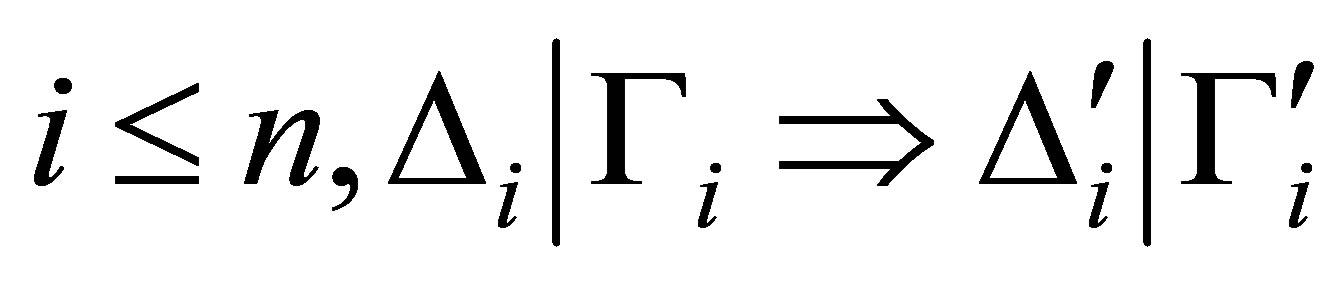 is either an axiom or deduced from the previous statements by the deduction rules.
is either an axiom or deduced from the previous statements by the deduction rules.
For example, the following
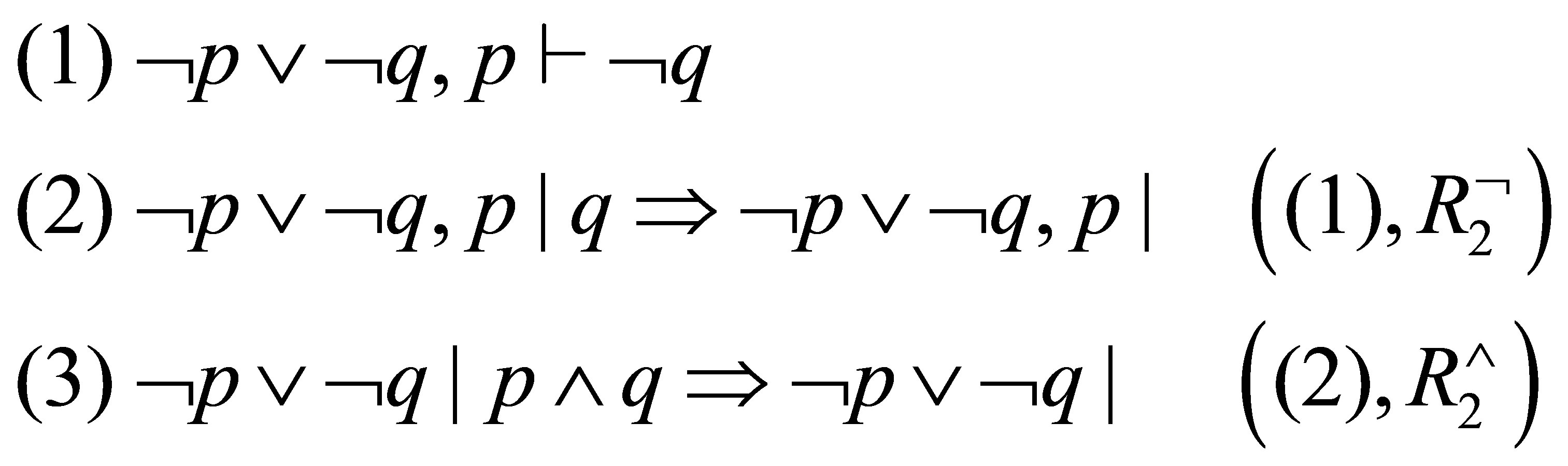
is a proof and so 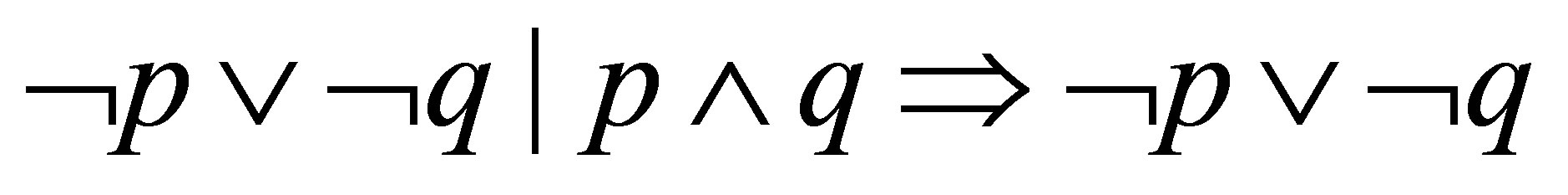 is provable.
is provable.
Also, the following

is a proof and so 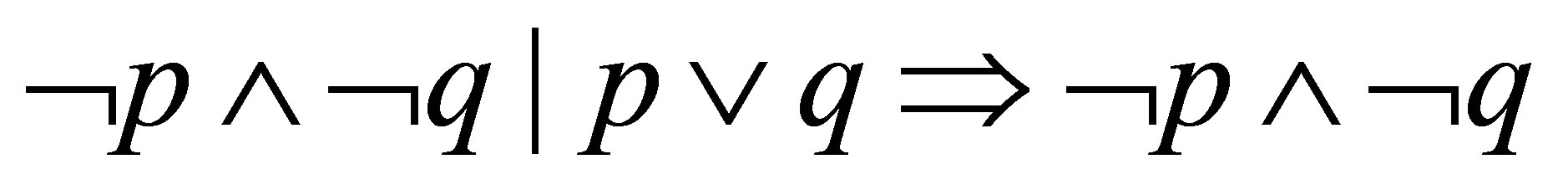 is provable.
is provable.
Theorem 3.3. For any consistent sets 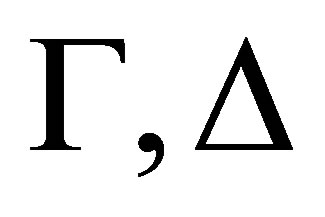 of formulas and formula
of formulas and formula 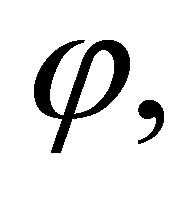 if
if 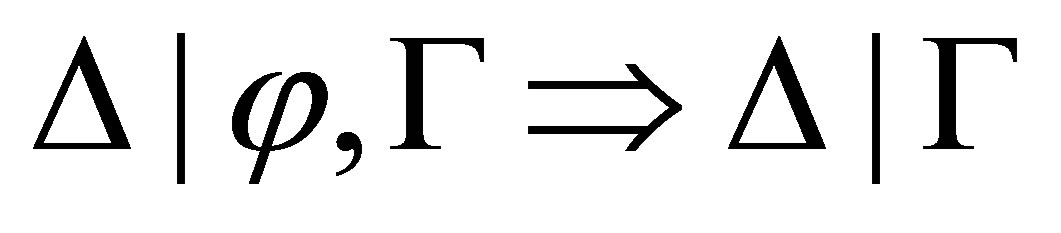 is provable then
is provable then  is inconsistent; and if
is inconsistent; and if  is provable then
is provable then  is consistent.
is consistent.
Proof. If  is provable then
is provable then 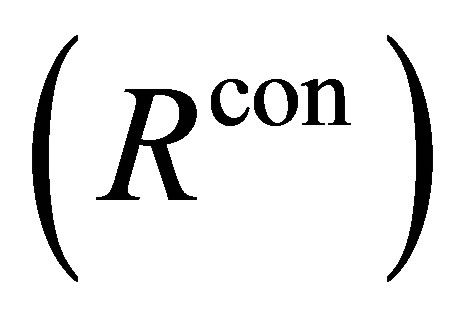 is used and
is used and  is consistent.
is consistent.
If 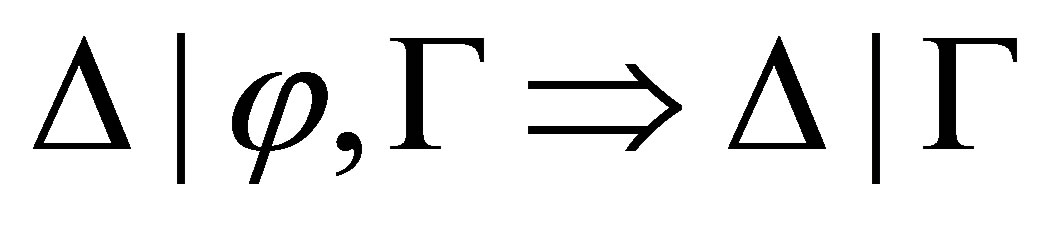 is provable then we prove that
is provable then we prove that 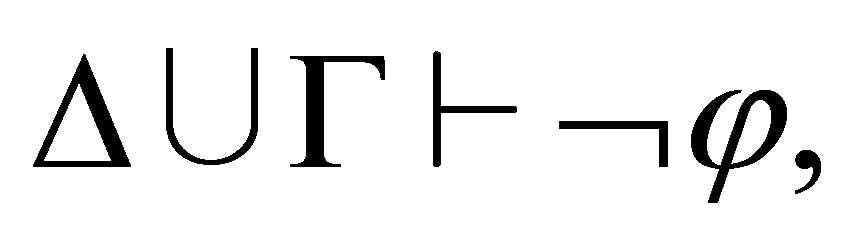 i.e.,
i.e.,  is inconsistent, by the induction on the length of a proof of
is inconsistent, by the induction on the length of a proof of 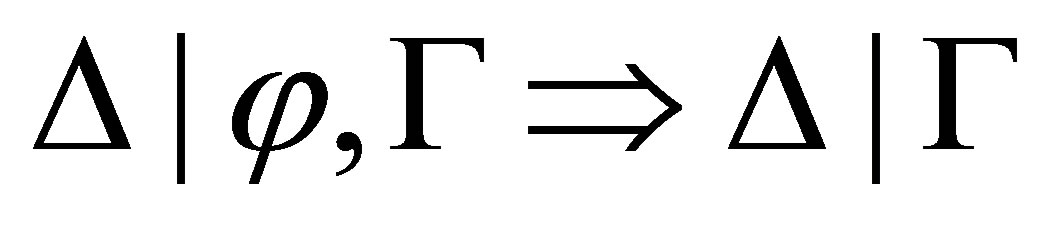 and the cases that the last inference rule is used.
and the cases that the last inference rule is used.
If the last rule used is 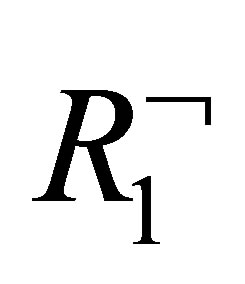 then
then 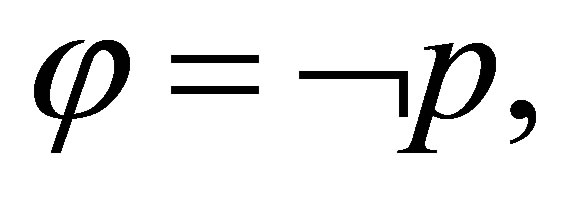 and
and  i.e.,
i.e., 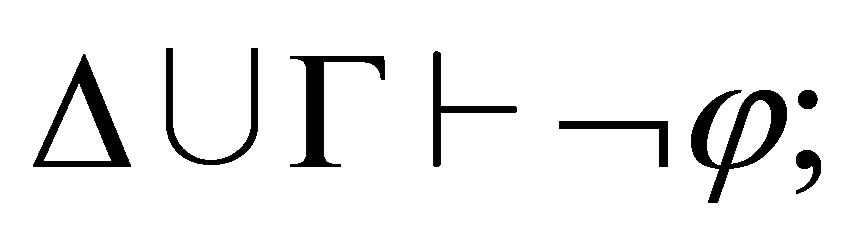
If the last rule used is 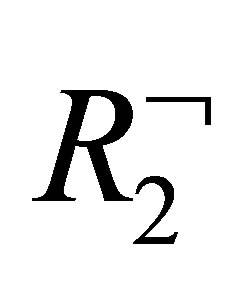 then
then 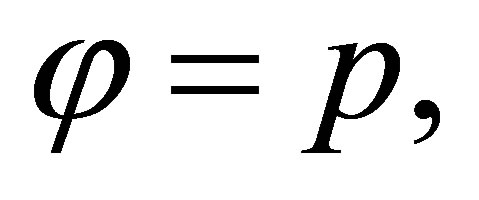 and
and 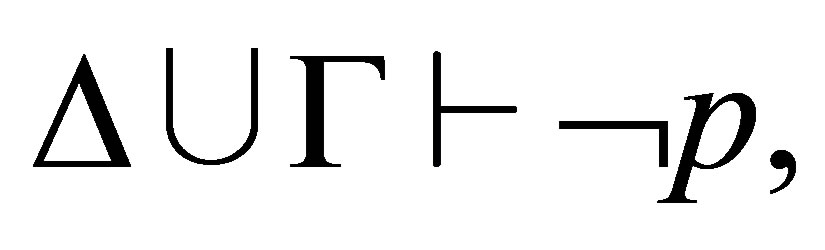 i.e.,
i.e., 
If the last rule used is  then
then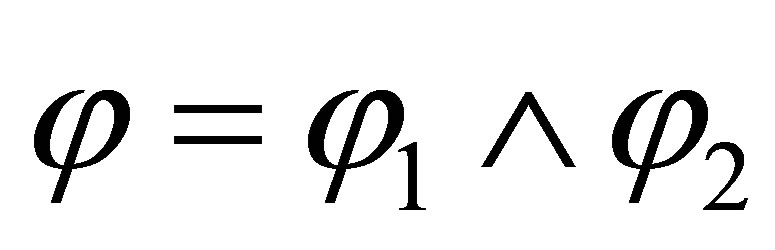 , and
, and  . By the induction assumption,
. By the induction assumption, 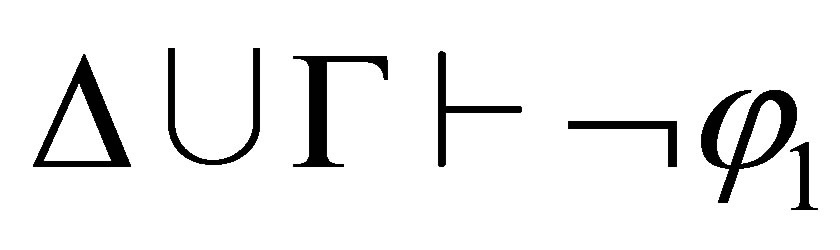 , and hence,
, and hence,  i.e.,
i.e., 
If the last rule used is 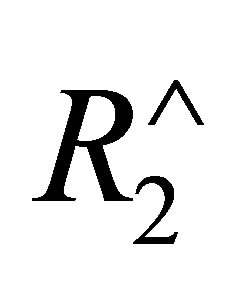 then
then 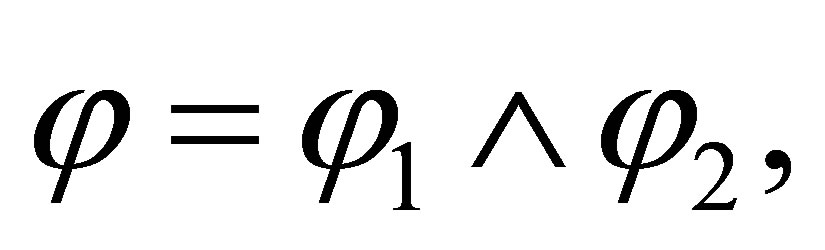 and
and 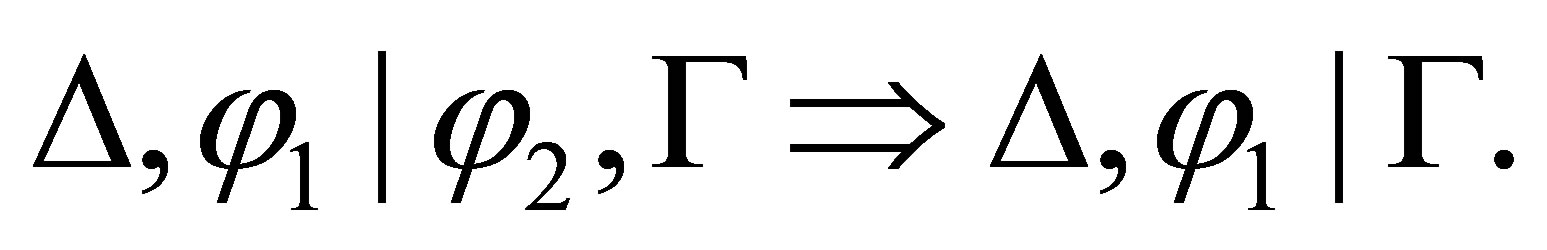 By the induction assumption,
By the induction assumption,  and hence,
and hence, 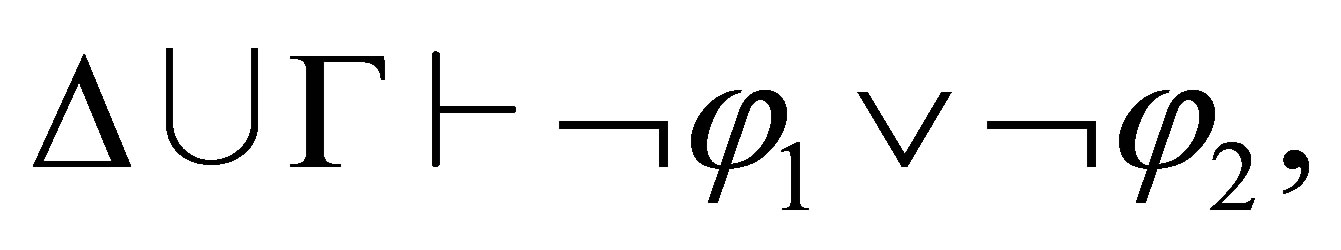 i.e.,
i.e., 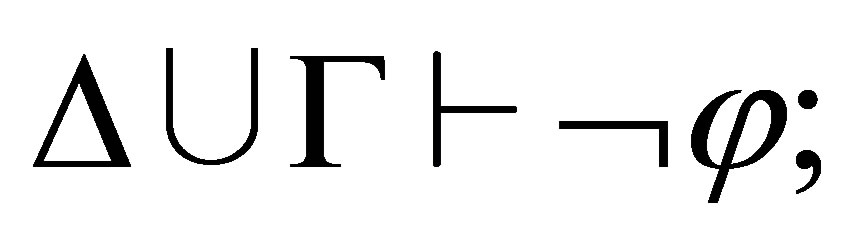
If the last rule used is  then
then 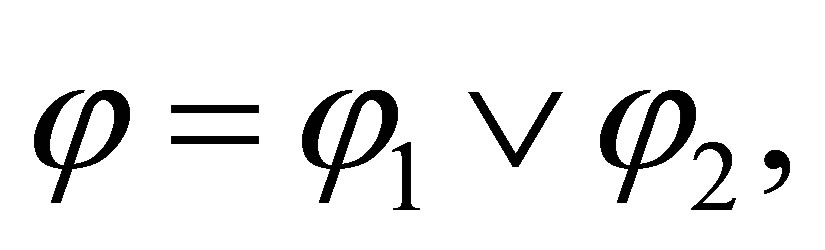 and
and
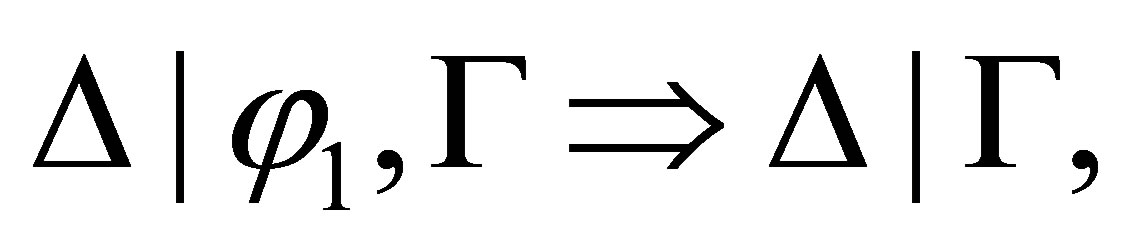
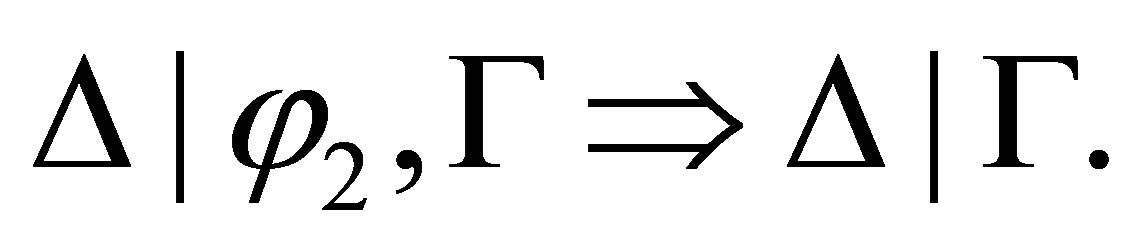
By the induction assumption,  ,
,  , and hence,
, and hence, 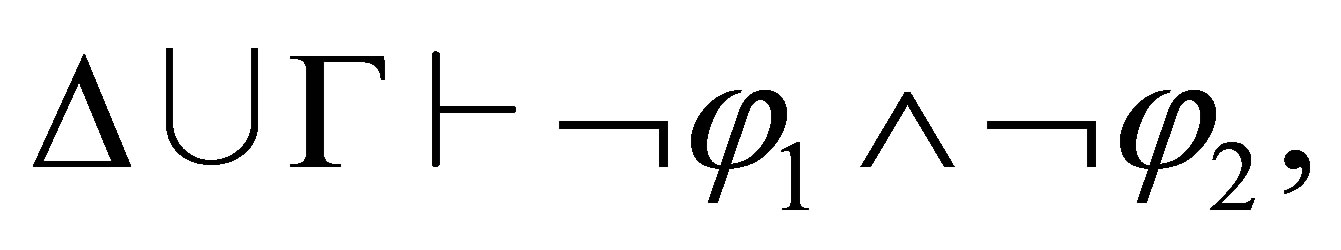 i.e.,
i.e., 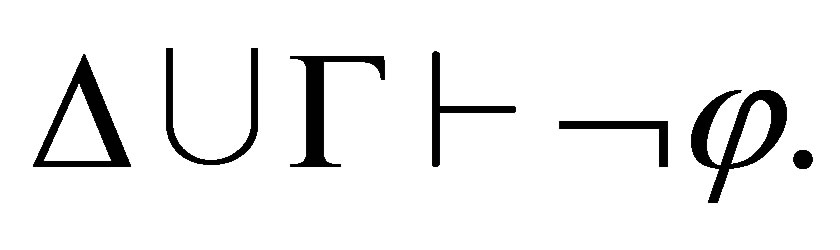
Theorem 3.4. For any consistent sets 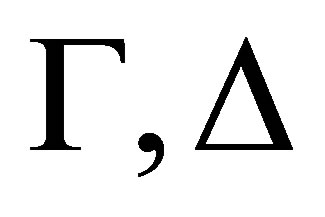 of formulas and formula φ, if
of formulas and formula φ, if  is inconsistent then
is inconsistent then  is provable; and if
is provable; and if  is consistent then
is consistent then  is provable.
is provable.
Proof. If φ is consistent with 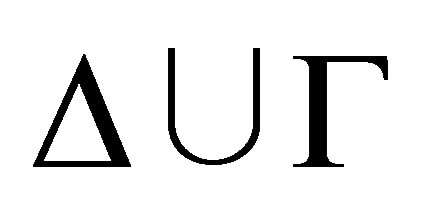 then by
then by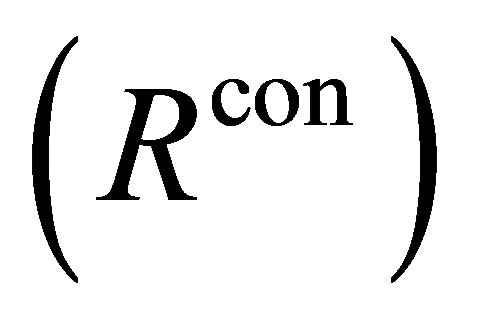 ,
, 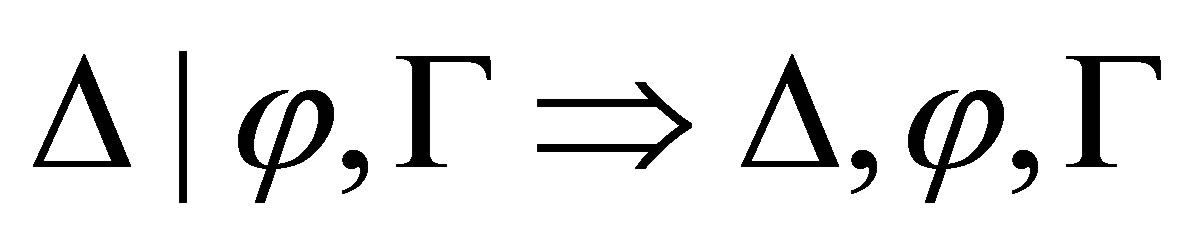 is provable;
is provable;
Assume that φ is inconsistent with Δ. We prove by the induction on the structure of φ that 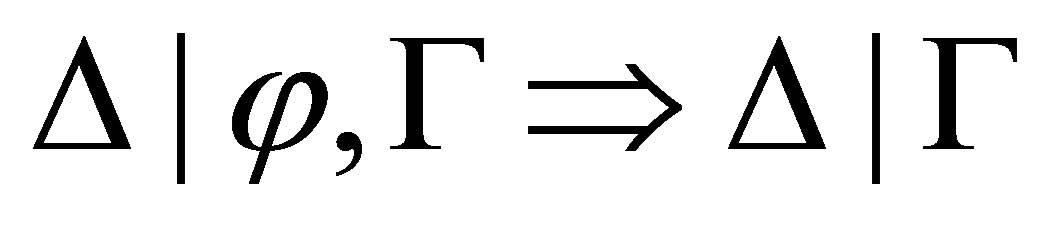 is provable.
is provable.
If φ = p then  and by
and by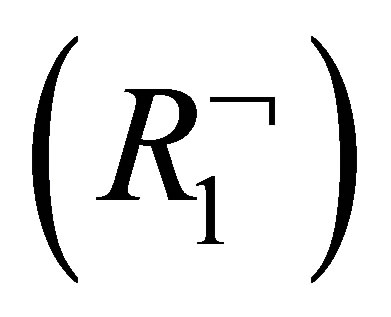 ,
, 
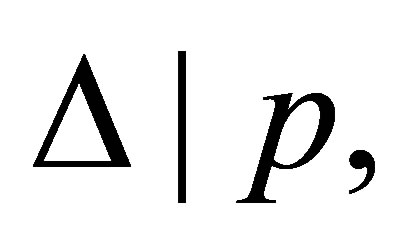 is provable.
is provable.
If 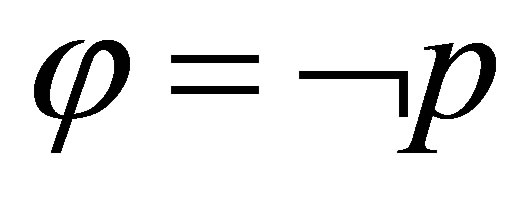 then
then  and by
and by 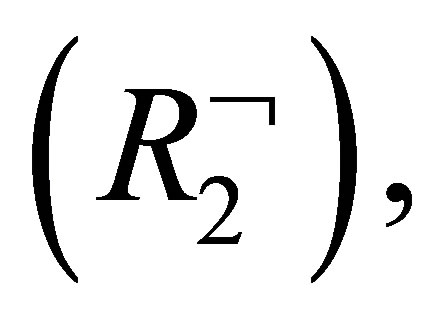

 is provable.
is provable.
If 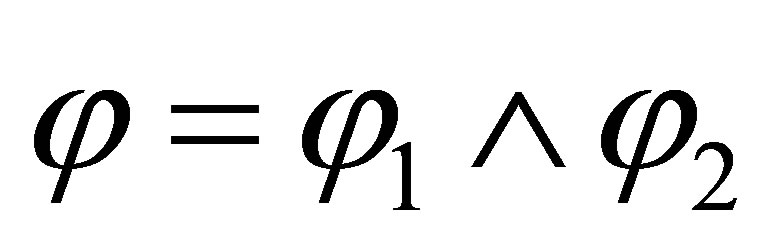 then there are two subcases:
then there are two subcases:  is inconsistent with
is inconsistent with  or
or 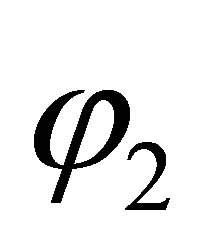 is consistent with
is consistent with 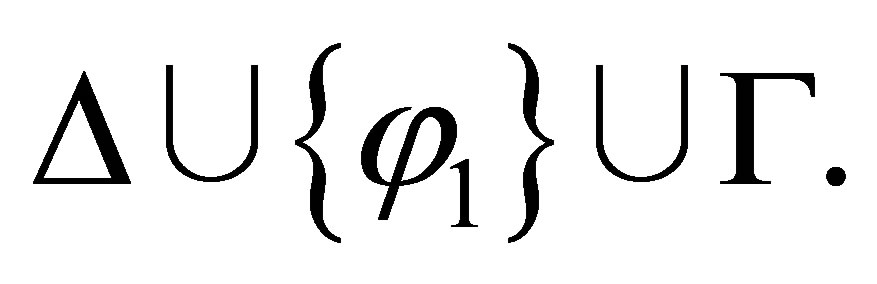 In the first subcase, by the induction assumption,
In the first subcase, by the induction assumption,  is provable, and by
is provable, and by 
 is provable; and in the second subcase,
is provable; and in the second subcase,  is consistent and
is consistent and 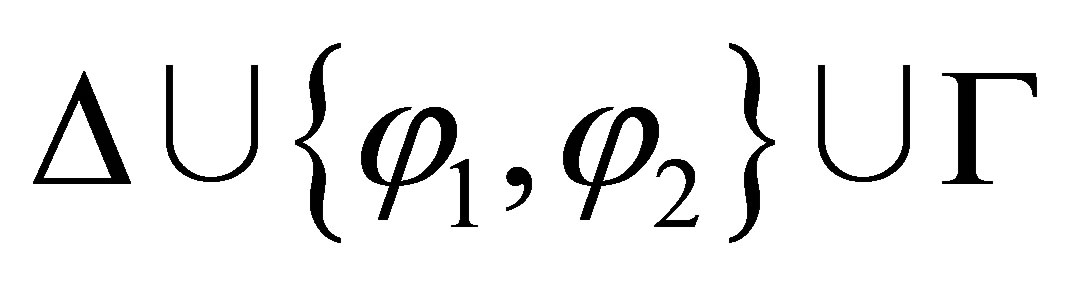 is inconsistent. By the induction assumption,
is inconsistent. By the induction assumption, 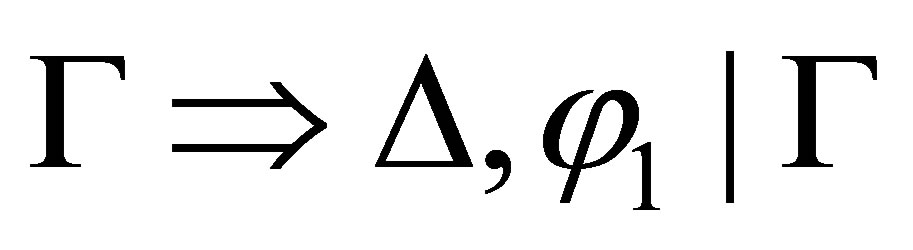
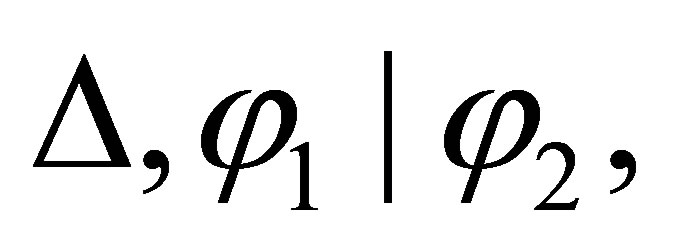 is provable, and by
is provable, and by 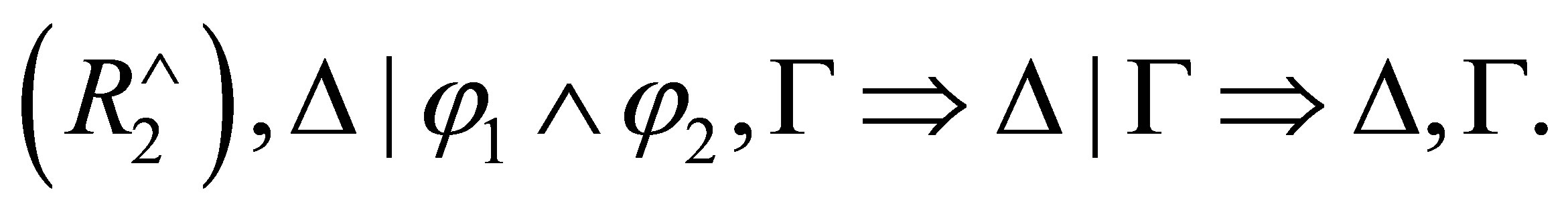
If 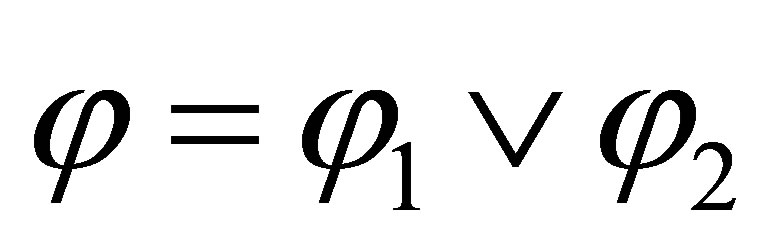 then both
then both  and
and  are inconsistent. By the induction assumption, both
are inconsistent. By the induction assumption, both  and
and 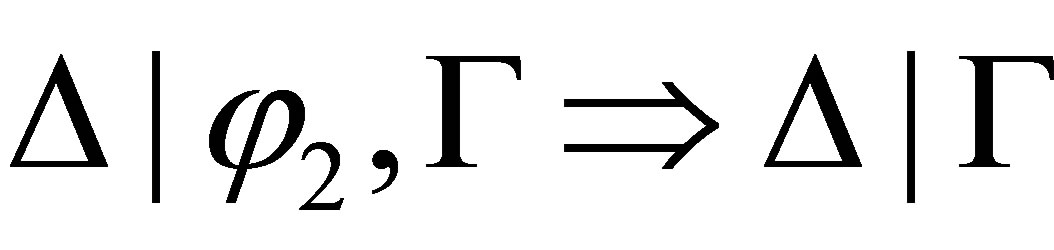 are provable, and by
are provable, and by  is provable.
is provable.
Theorem 3.5. For any consistent sets 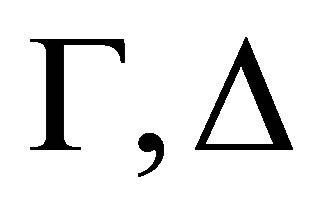 of formulas, if
of formulas, if 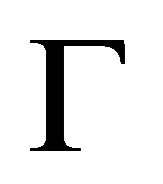 is finite then there is a set
is finite then there is a set 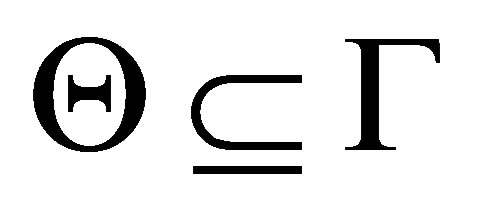 of formulas such that
of formulas such that 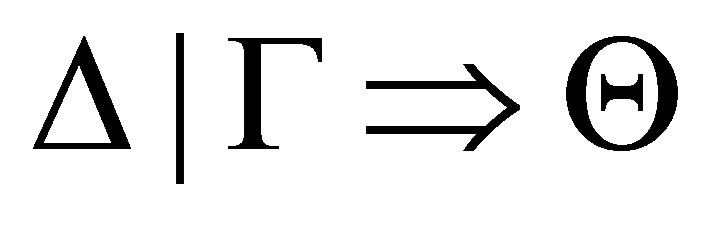 is provable Proof. Let
is provable Proof. Let 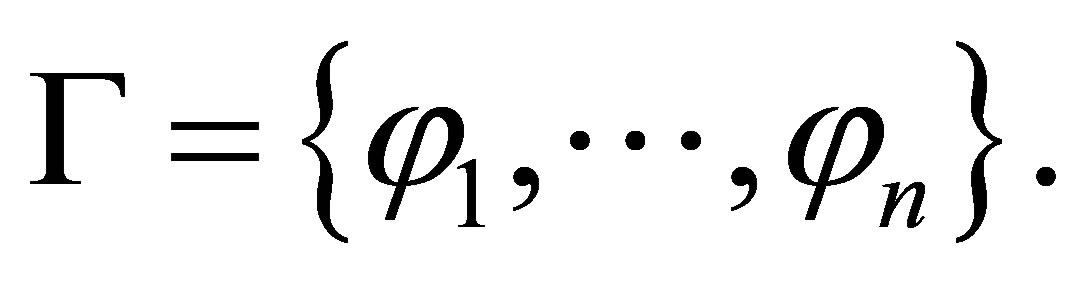
We prove the theorem by the induction on 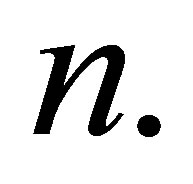
If 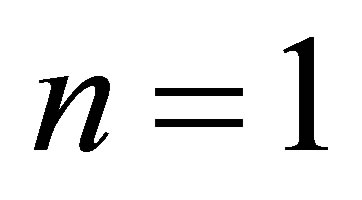 then by theorem 3.3, let
then by theorem 3.3, let
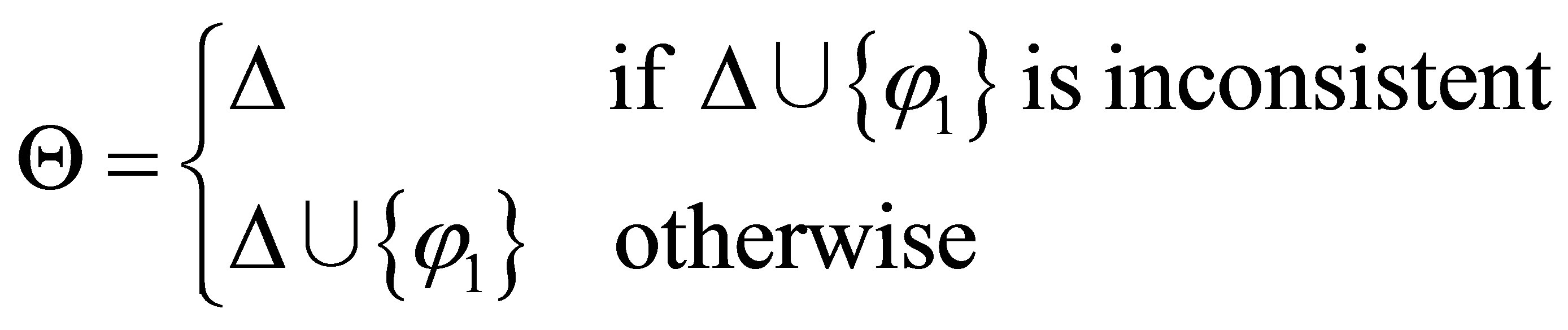
and  satisfies the theorem.
satisfies the theorem.
Assume that the theorem holds for 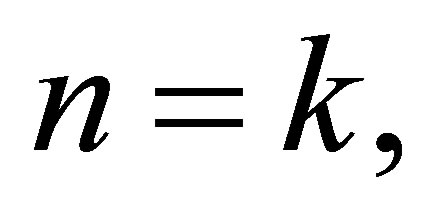 that is, there is a set
that is, there is a set  such that
such that 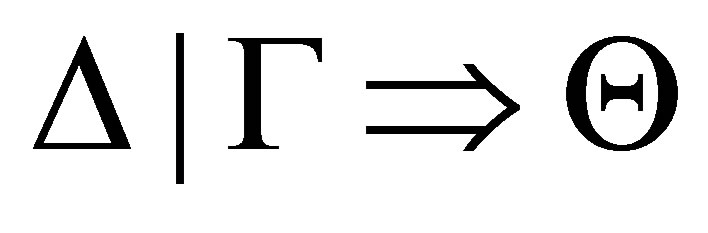 is provable. Let
is provable. Let 
If 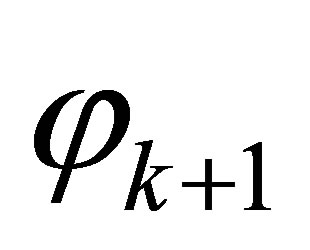 is consistent with
is consistent with  then
then 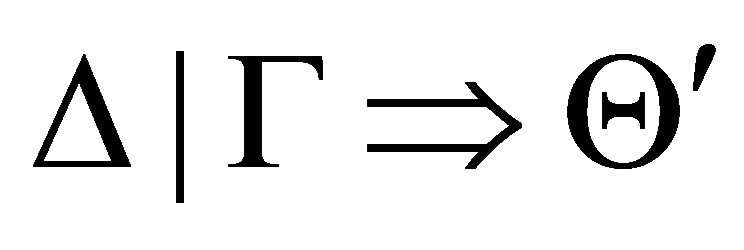 is provable, where
is provable, where 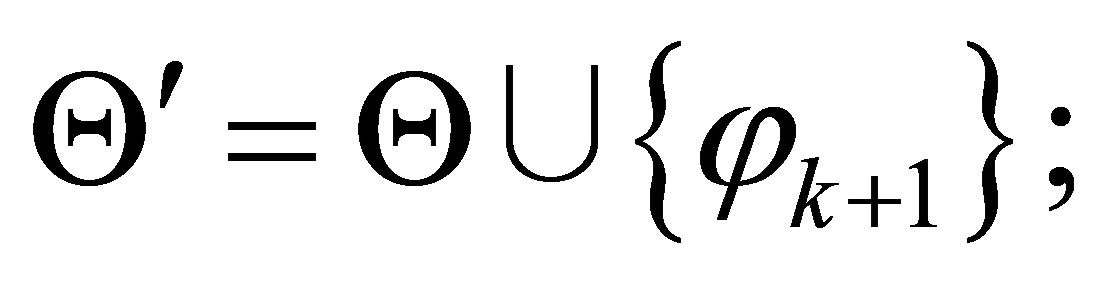
If 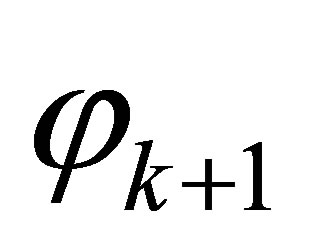 is inconsistent with
is inconsistent with  then
then
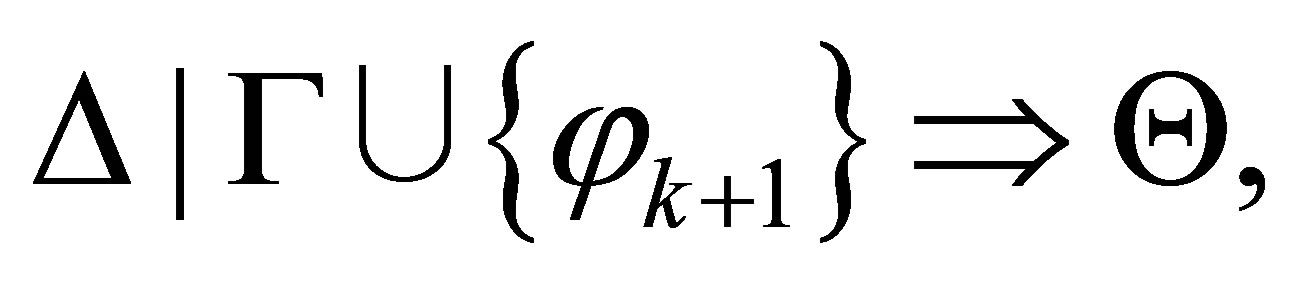 because the last formula
because the last formula  is inconsistent with
is inconsistent with 
Theorem 3.6 (The soundness theorem for ). If
). If 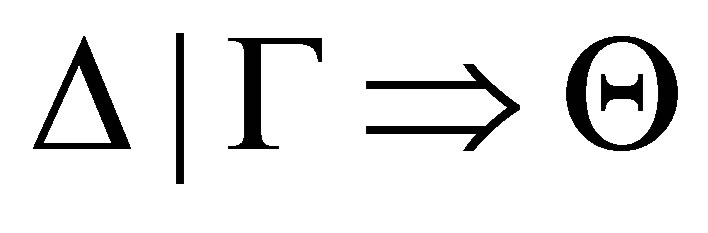 is provable then
is provable then  is a pseudo-revision of
is a pseudo-revision of 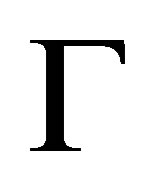 by
by 
Proof. Firstly we prove that if  is provable then
is provable then  is a pseudo-revision of
is a pseudo-revision of  by
by 
Assume that 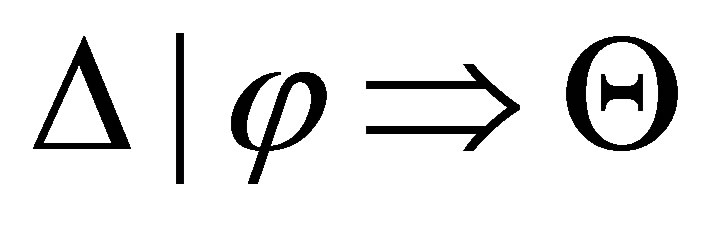 is provable.
is provable.
If 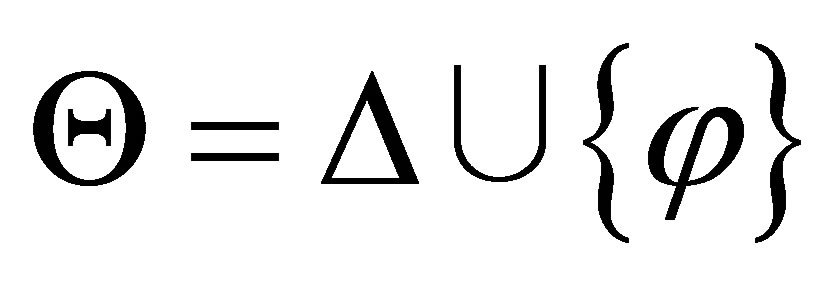 then
then  is consistent with
is consistent with  and
and  is a pseudo-revision of
is a pseudo-revision of  by
by 
If 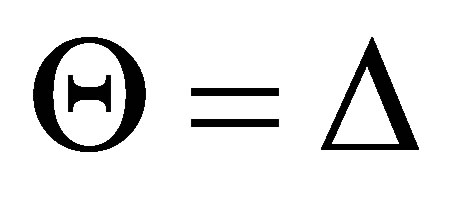 then
then  is inconsistent with φ,
is inconsistent with φ, 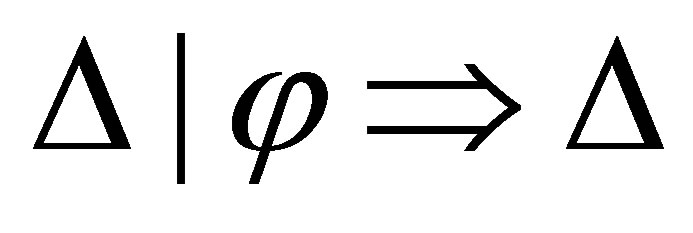 is provable, and
is provable, and  is a pseudo-revision of
is a pseudo-revision of  by
by 
Similarly, by the induction on the number of formulas in  we can prove that if
we can prove that if  then
then  is a pseudo-revision of
is a pseudo-revision of  by
by .
.
Theorem 3.7 (The completeness theorem for ). If
). If  is a pseudo-revision of
is a pseudo-revision of 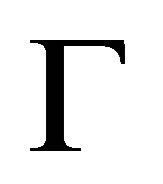 by
by  then
then 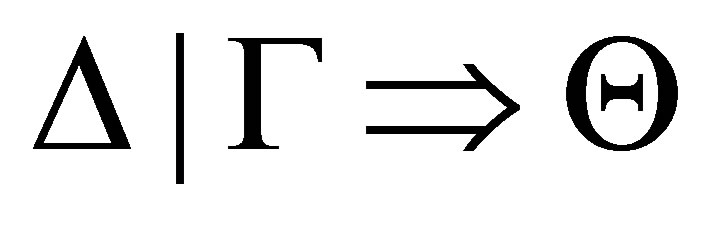 is provable.
is provable.
Proof. Let  be a pseudo-revision of Γ by
be a pseudo-revision of Γ by  under the ordering
under the ordering  of Γ.
of Γ.
We prove by induction on 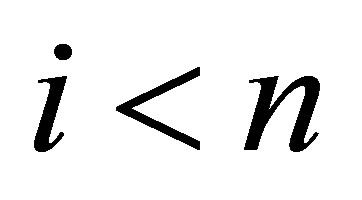 that there is a formula set
that there is a formula set  such that
such that 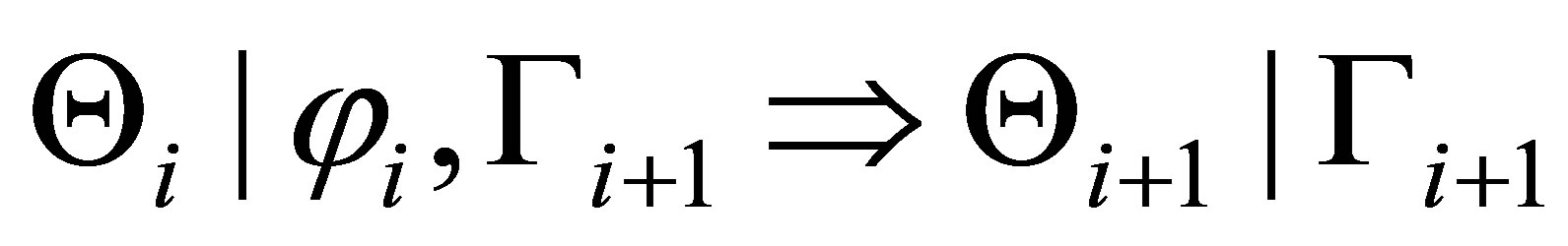 is provable, where
is provable, where 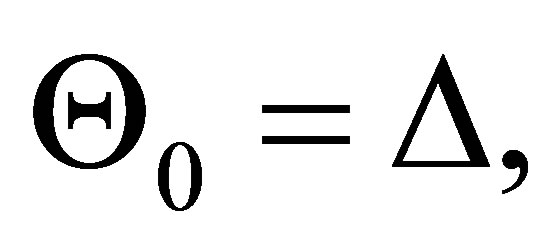 and
and 
If 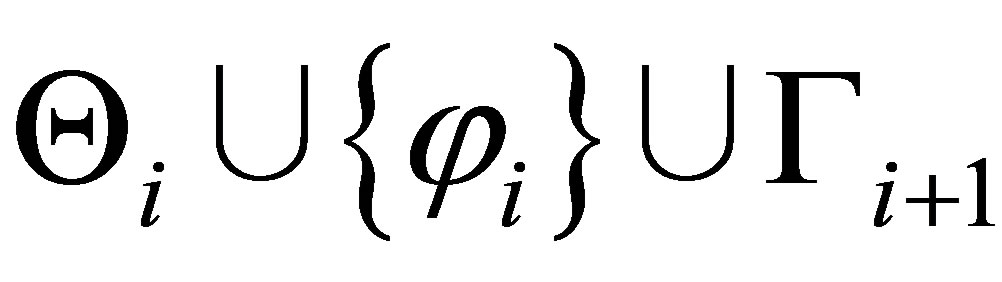 is consistent then let
is consistent then let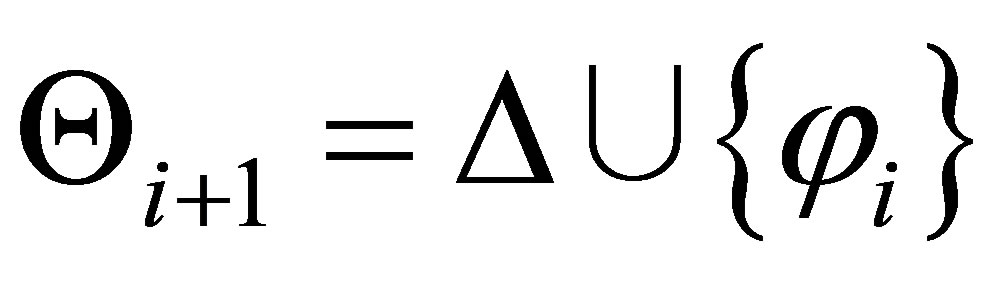 , and
, and 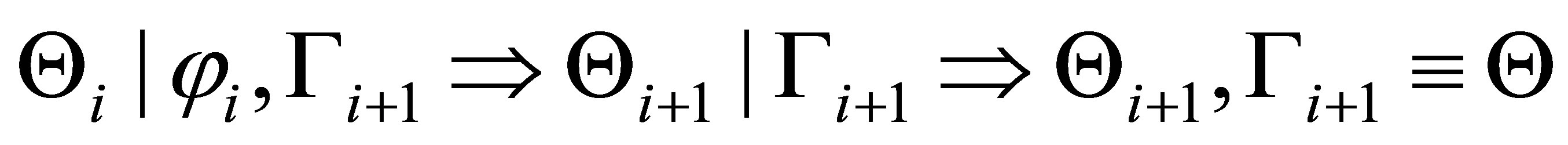 is provable, where
is provable, where 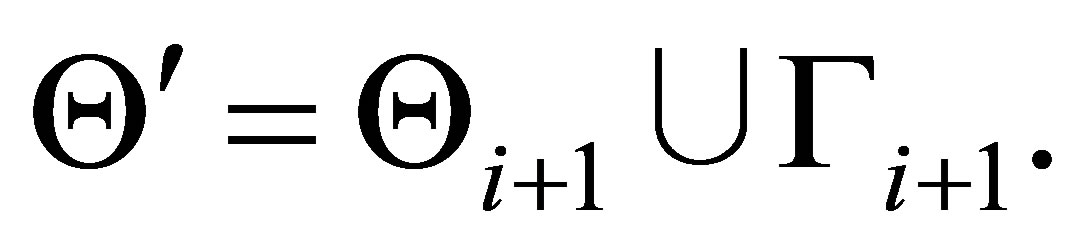
Assume that 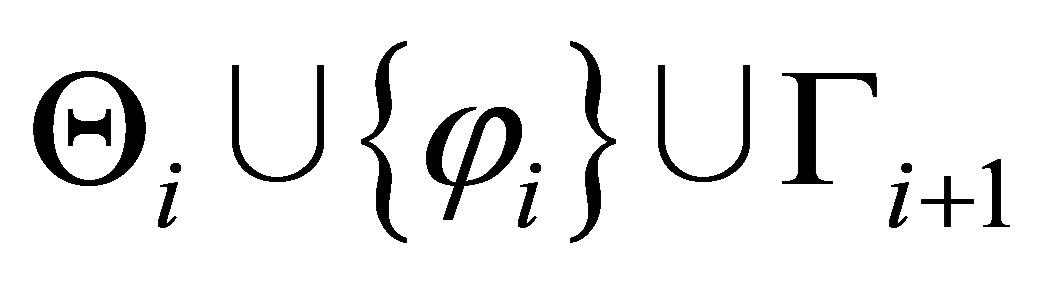 is inconsistent. Then,
is inconsistent. Then,  and let
and let 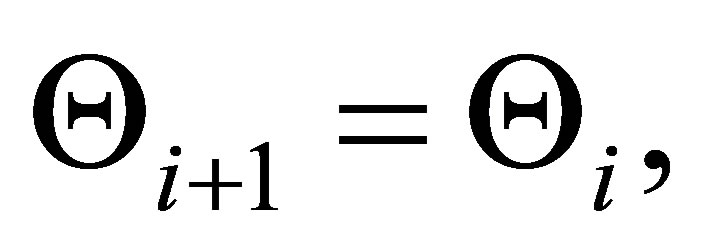 by theorem 3.4,
by theorem 3.4,
 is provable.
is provable.
Let 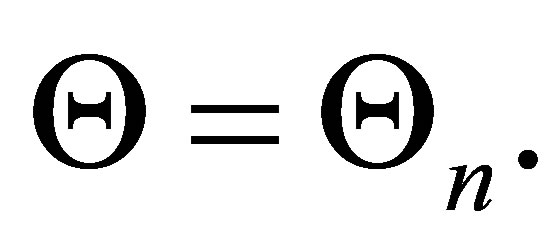 Then,
Then,  is provable.
is provable.
4. The  -Calculus
-Calculus 
In this section we give an  -calculus
-calculus 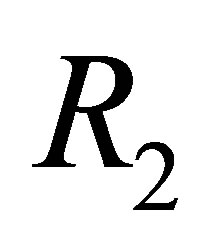 which is sound and complete with respect to the pre-revision, where the decision of whether
which is sound and complete with respect to the pre-revision, where the decision of whether  is consistent is deduced by a set of
is consistent is deduced by a set of 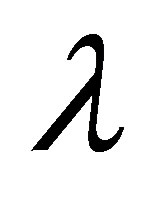 -rules.
-rules.
R1 is used to reduce  to
to  when
when  is inconsistent. When
is inconsistent. When  is consistent, there are subformulas in
is consistent, there are subformulas in  which is inconsistent with
which is inconsistent with  we hope to reduce those subformulas into the empty string. For example, let
we hope to reduce those subformulas into the empty string. For example, let
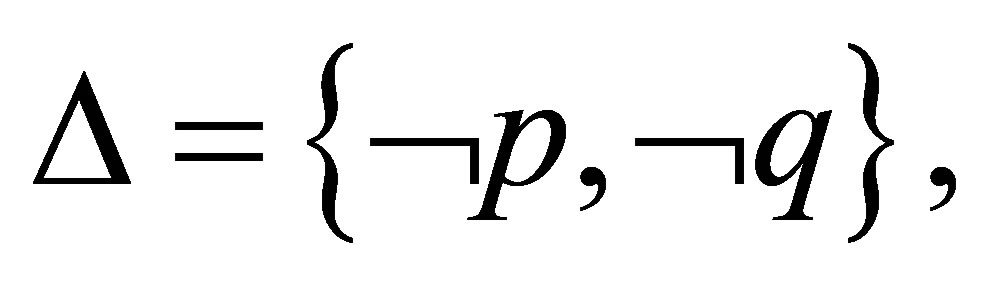
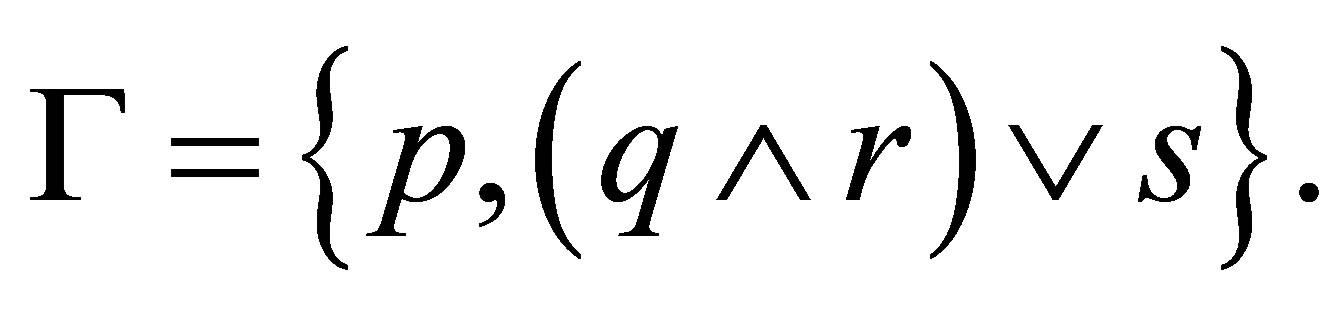
Then, by 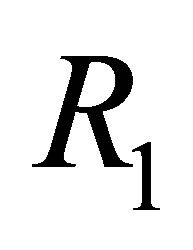 we have the following reduction:
we have the following reduction:
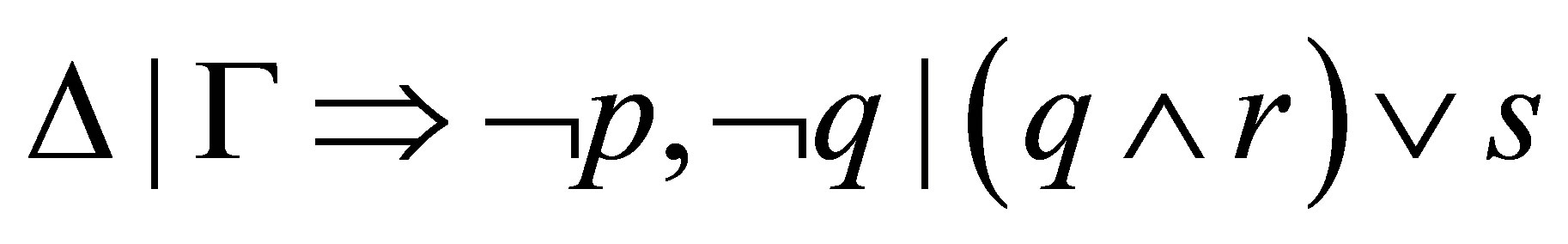

and by  we shall have the following one:
we shall have the following one:
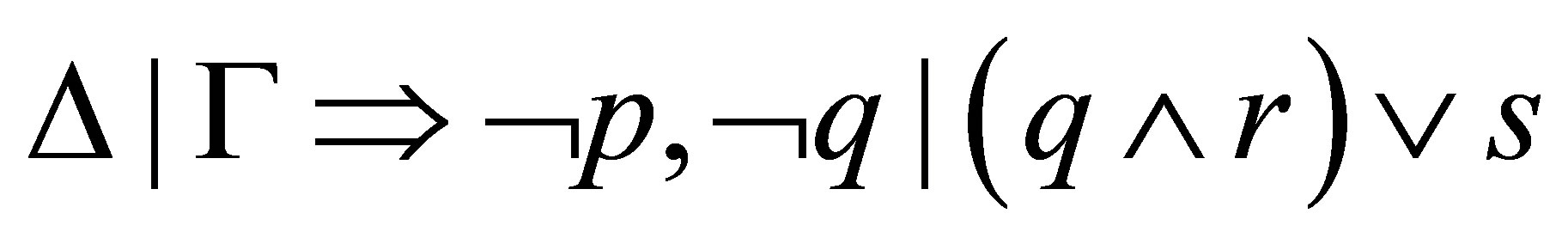
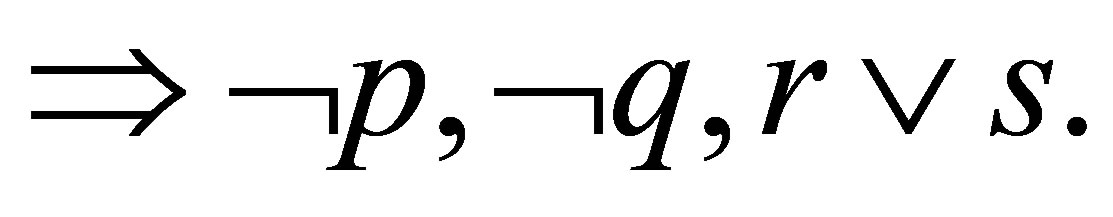
For the two reductions, we have
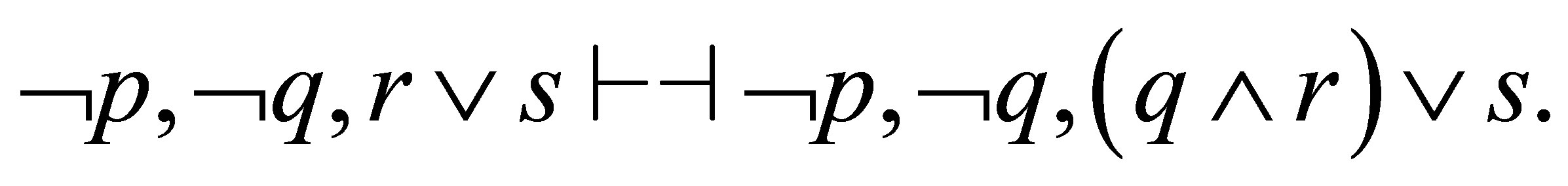
Let  be a consistent set of formulas and
be a consistent set of formulas and 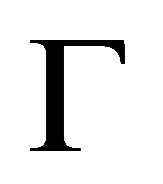 a finite consistent set of formulas.
a finite consistent set of formulas.
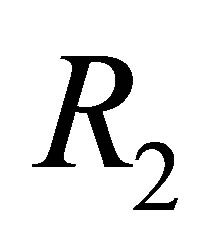 consists of two parts:
consists of two parts: 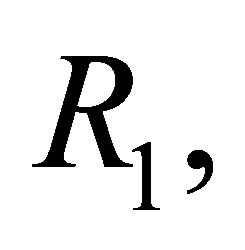 which we use to decompose formula
which we use to decompose formula  in
in  if
if  is inconsistent; and
is inconsistent; and 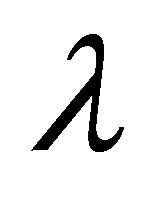 -deduction rules, which we use to decompose
-deduction rules, which we use to decompose  if
if  is consistent.
is consistent.
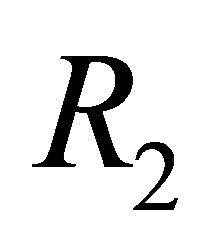 has the following
has the following 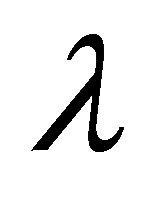 -deduction rules to reduce
-deduction rules to reduce 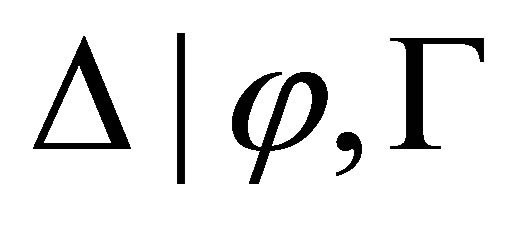 when
when  is consistent:
is consistent:
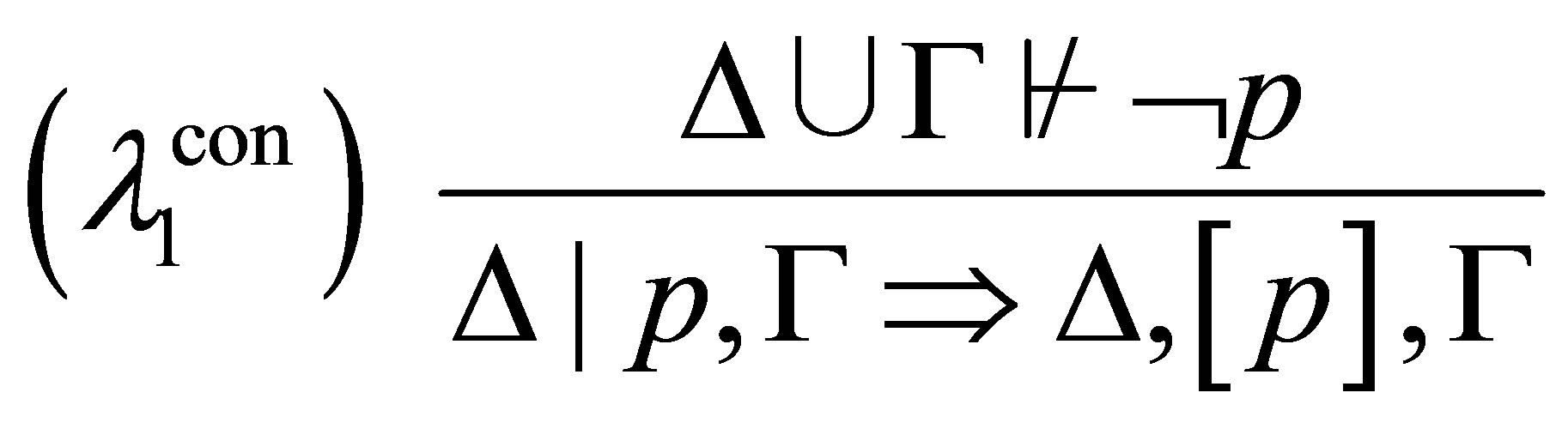

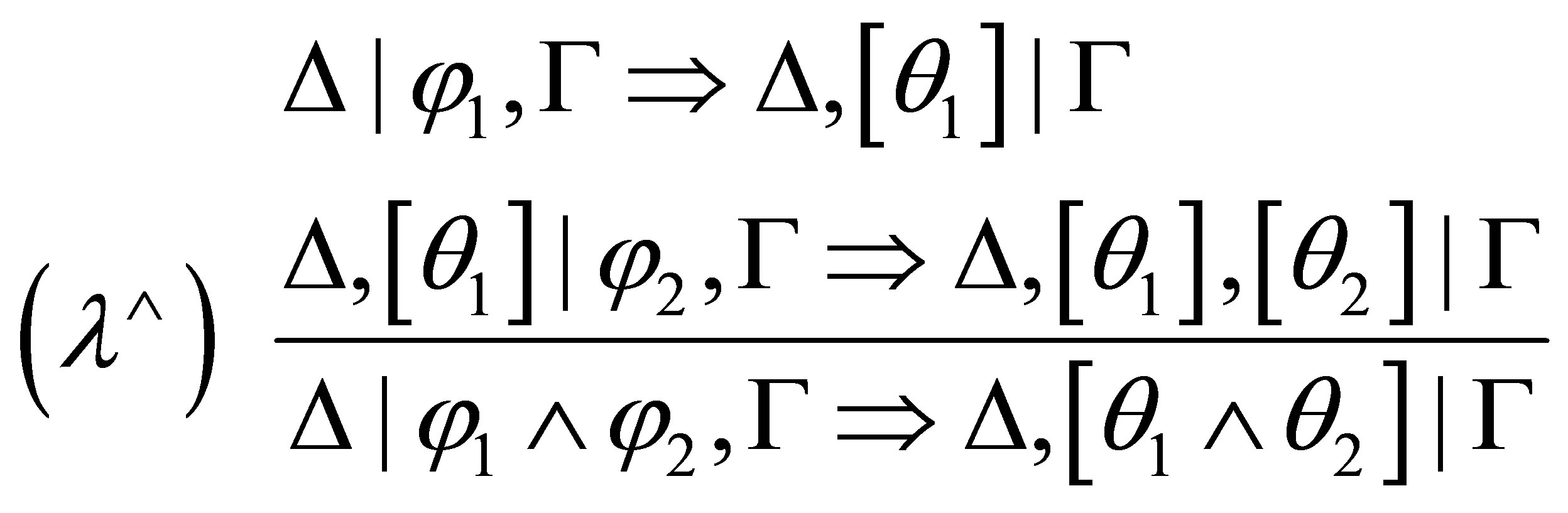
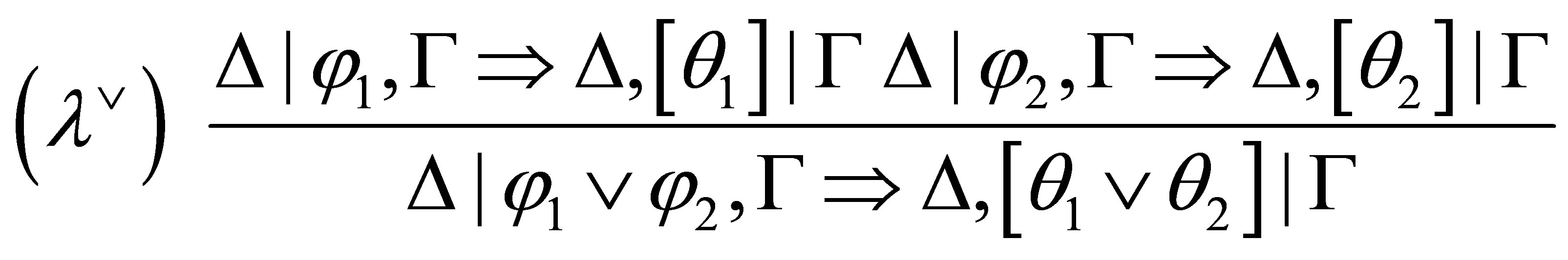
where if  is consistent then
is consistent then
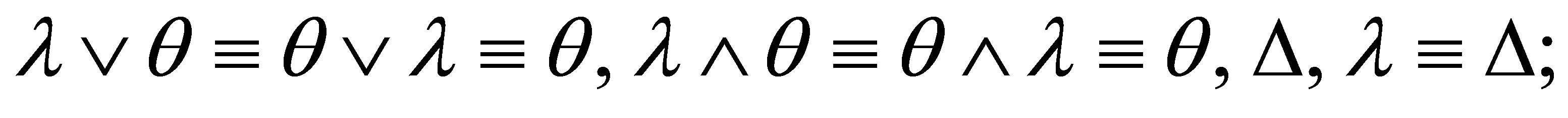
and if  is inconsistent then
is inconsistent then
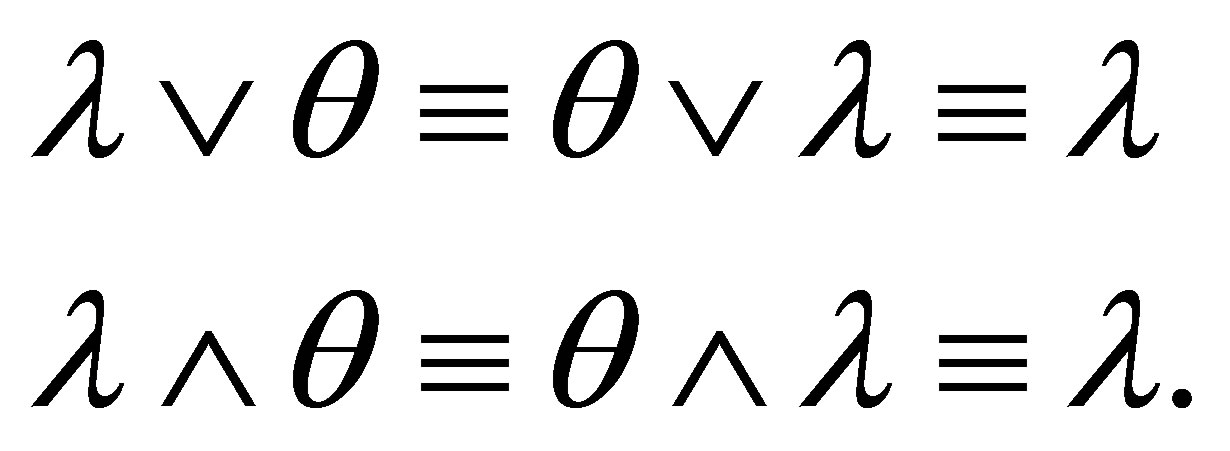
The deductions for the inconsistent  are the same as in
are the same as in  minus
minus 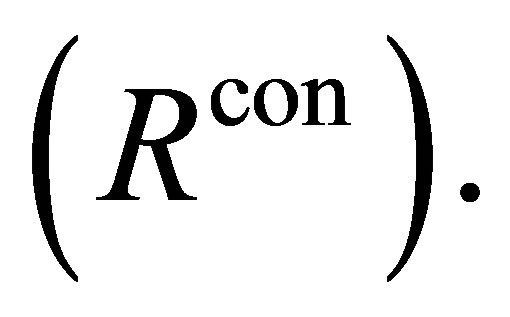
Definition 4.1. 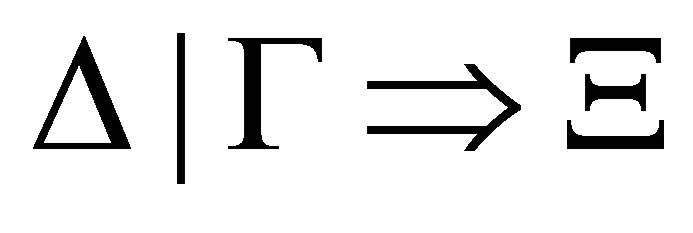 is provable if there is a sequence
is provable if there is a sequence
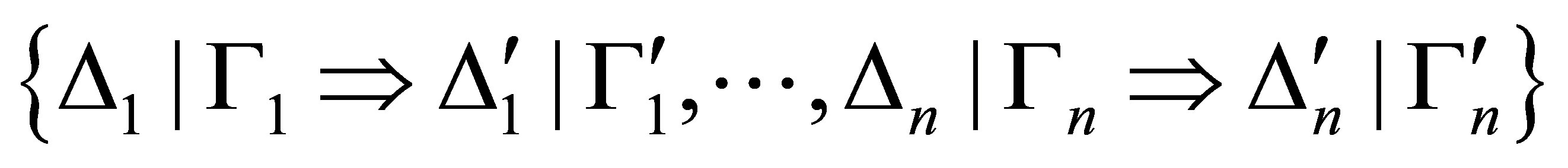
of statements such that 1) 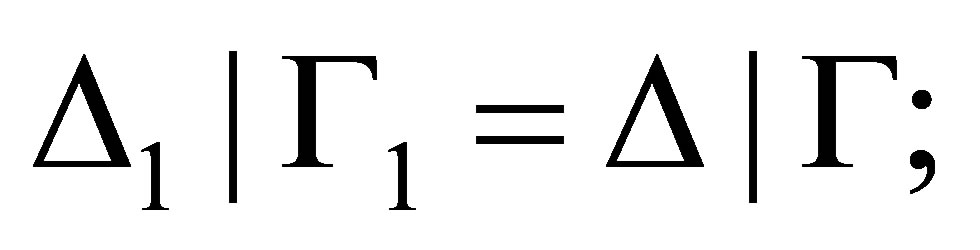
2) 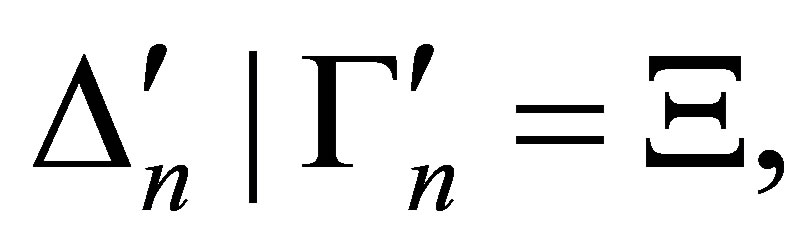 and 3) for each
and 3) for each 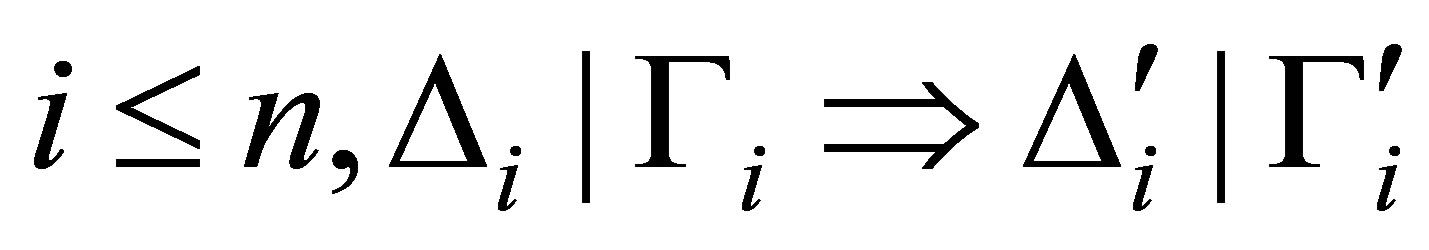 is either an axiom or deduced from the previous statements by the deduction rules.
is either an axiom or deduced from the previous statements by the deduction rules.
We call the sequence a proof of statement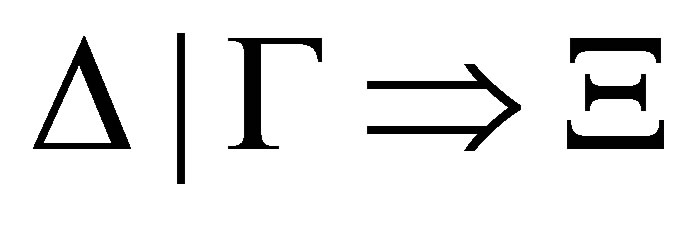 .
.
For example, the following
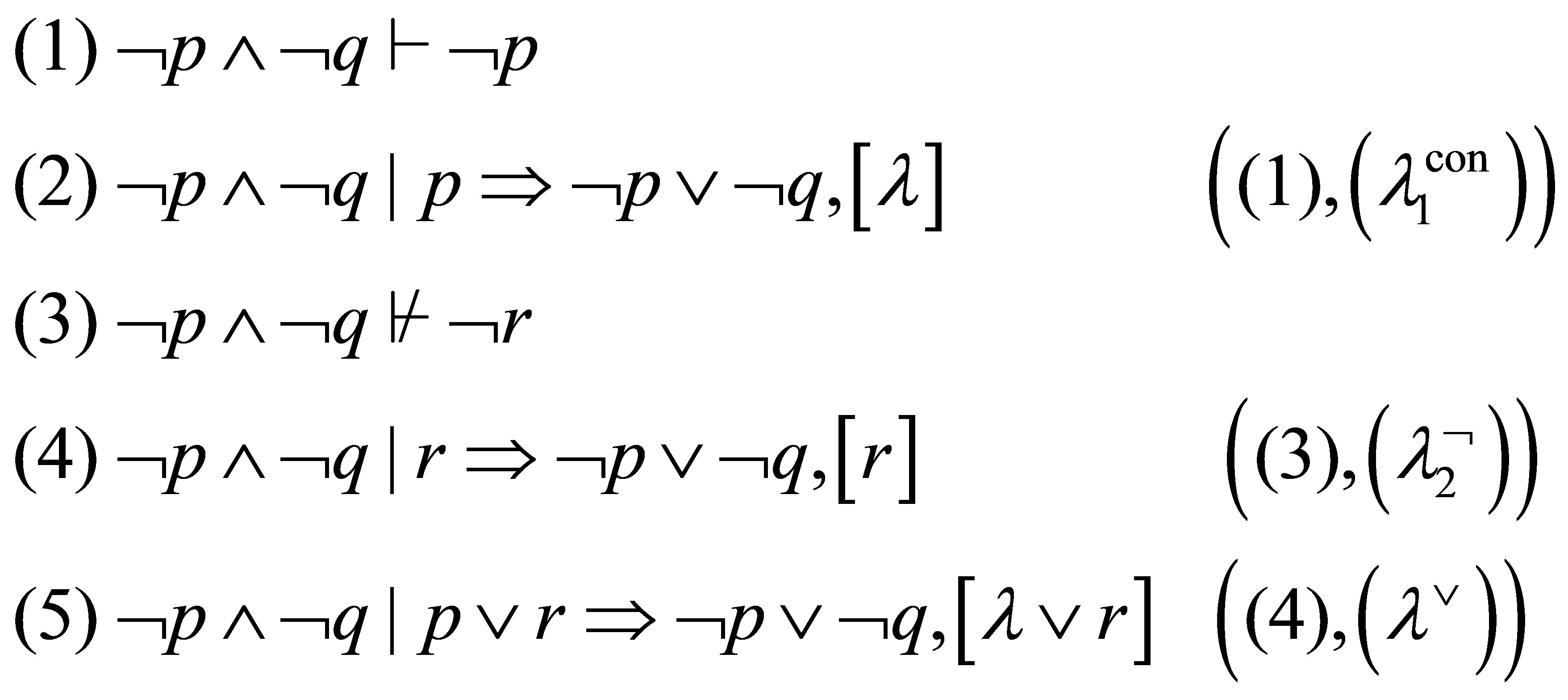
is a proof and  is provable.
is provable.
Theorem 4.2. For any consistent sets 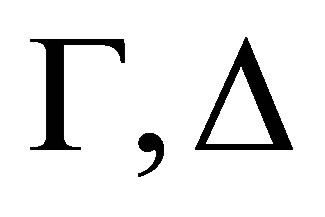 of formulas and formula
of formulas and formula  if
if 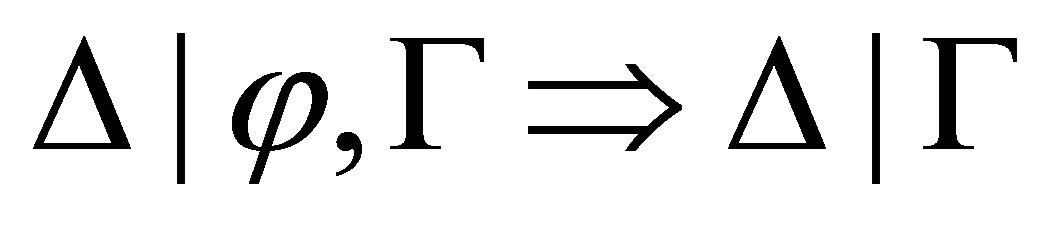 is provable then
is provable then  is inconsistent; and if there is a formula
is inconsistent; and if there is a formula  such that
such that 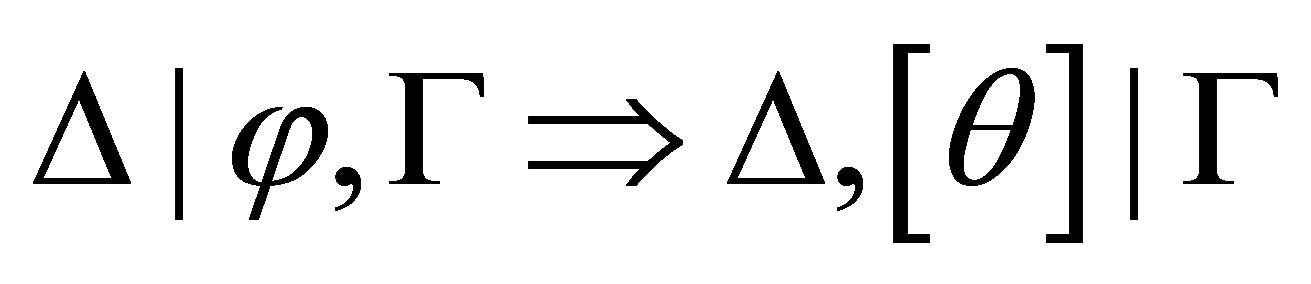 is provable then
is provable then  is consistent.
is consistent.
Proof. If 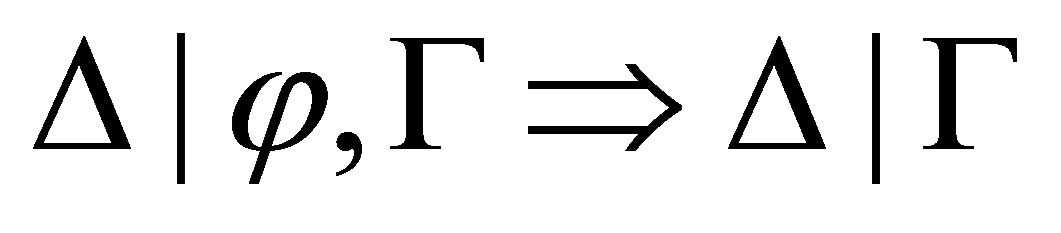 is provable then similar to the proof of theorem 3.3,
is provable then similar to the proof of theorem 3.3,  is inconsistent.
is inconsistent.
Assume that there is a formula 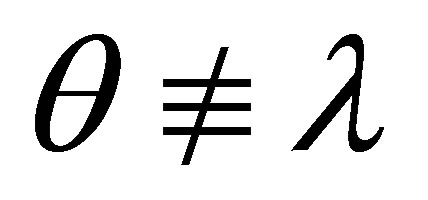 such that
such that  is provable. We prove by the induction on the length of a proof of
is provable. We prove by the induction on the length of a proof of 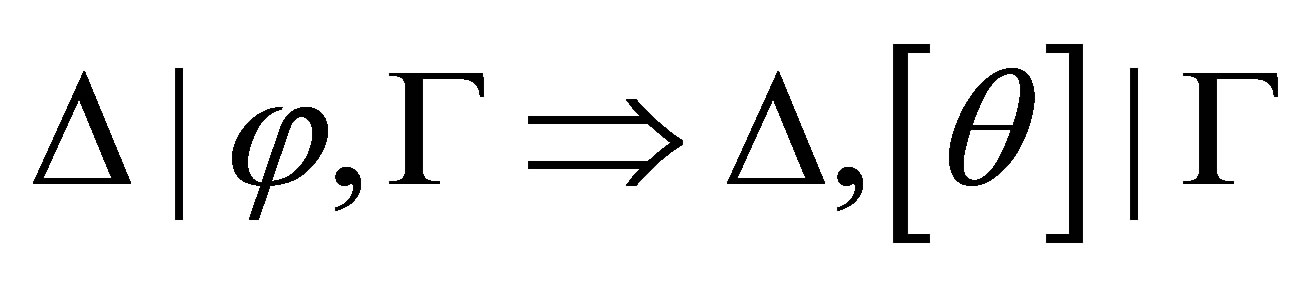 and the cases that the last inference rule is used that
and the cases that the last inference rule is used that  is consistent.
is consistent.
If the last rule used is  then
then  and
and 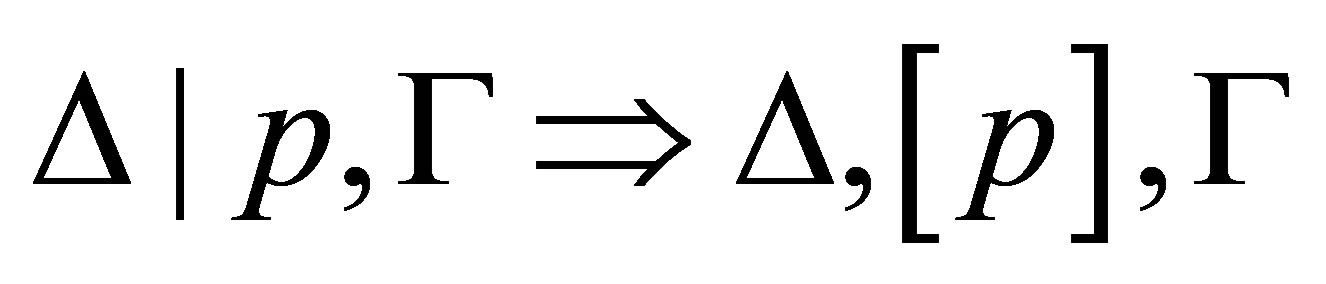 is provable, where
is provable, where 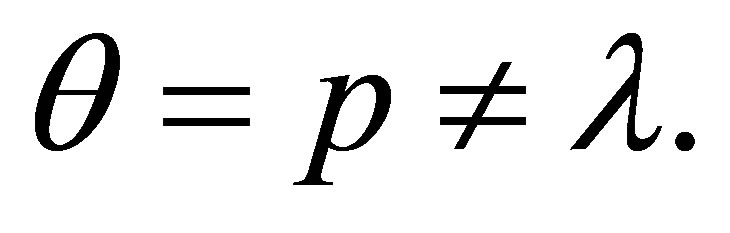 Hence,
Hence,  is consistent.
is consistent.
If the last rule used is 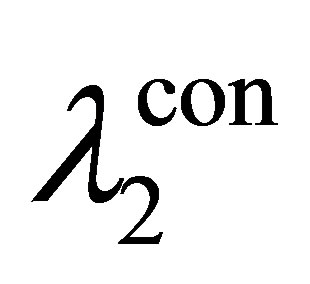 then
then 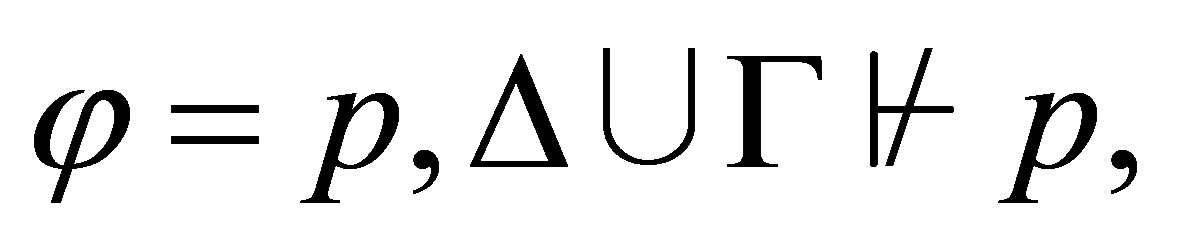 and
and 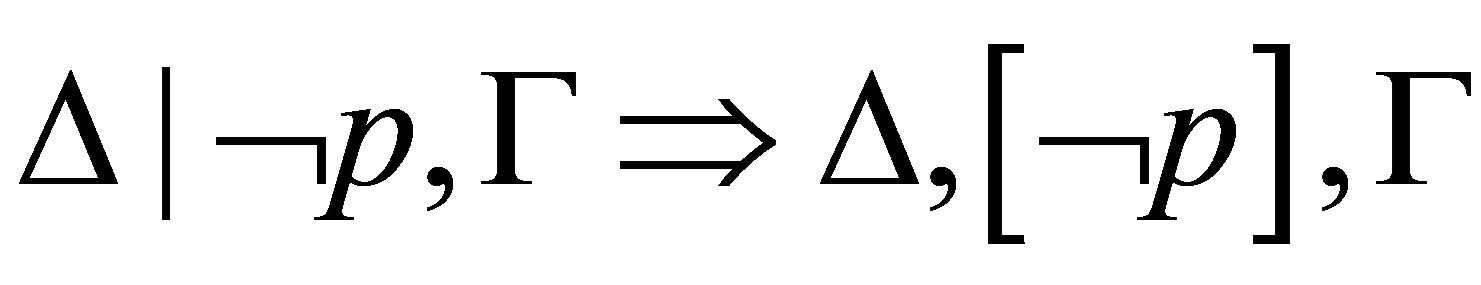 is provable, where
is provable, where 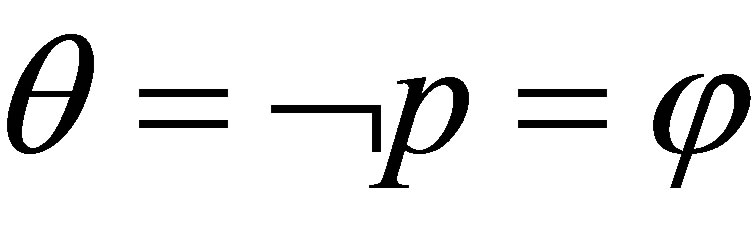 . Hence,
. Hence,  is consistent.
is consistent.
If the last rule used is 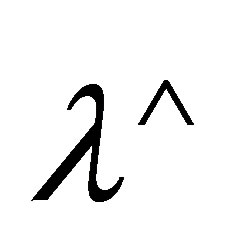 then
then 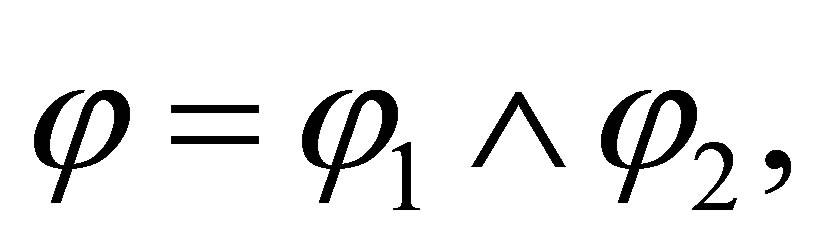 and there are formulas
and there are formulas 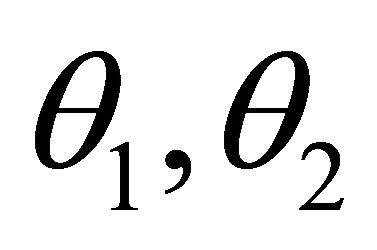 such that
such that

and

By the induction assumption, if θ1 ≠ λ and θ2 ≠ λ then  is consistent and
is consistent and 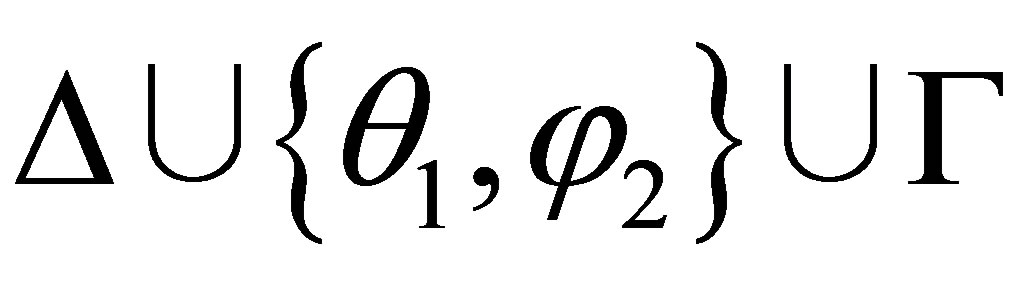 is consistent, and therefore,
is consistent, and therefore,  is consistent.
is consistent.
If the last rule used is  then
then 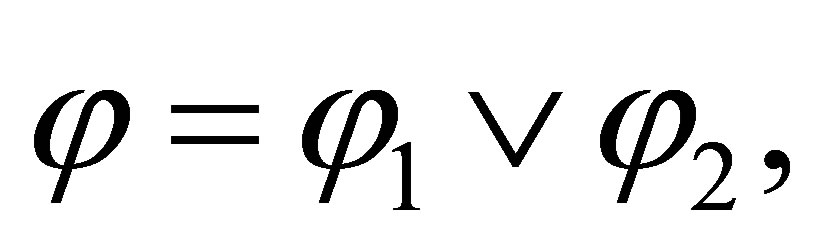 and
and

where either 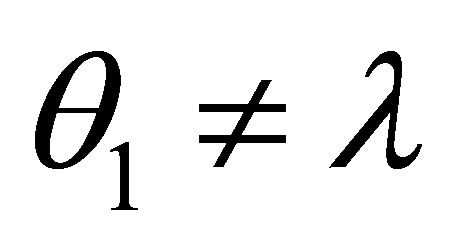 or
or 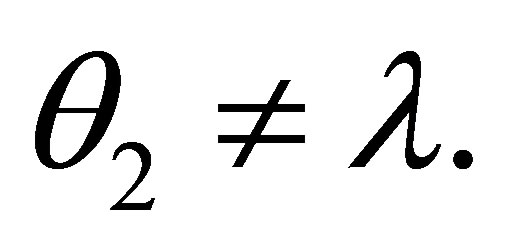
If θ1 ≠ λ and θ2 ≠ λ then by the induction assumption,  and
and 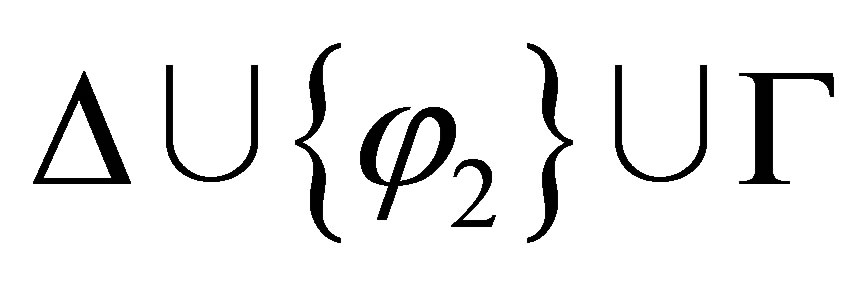 are consistent, and so is
are consistent, and so is 
If θ1 ≠ λ and θ2 ≠ λ then by the induction assumption,  is consistent, and so is
is consistent, and so is 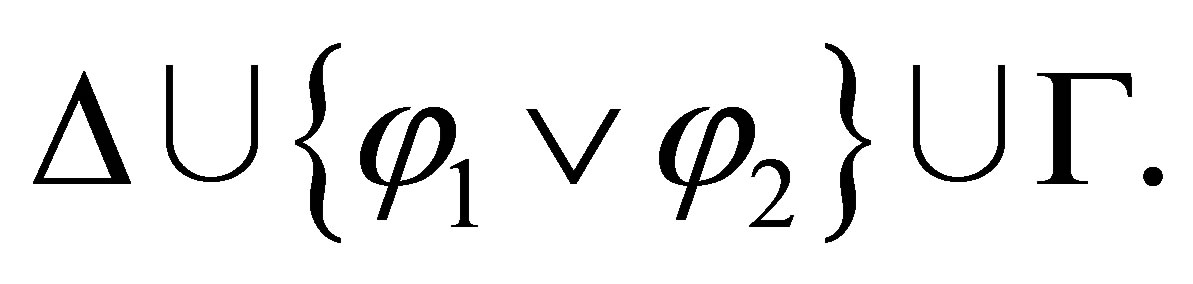
If θ1 ≠ λ and θ2 ≠ λ then by the induction assumption, 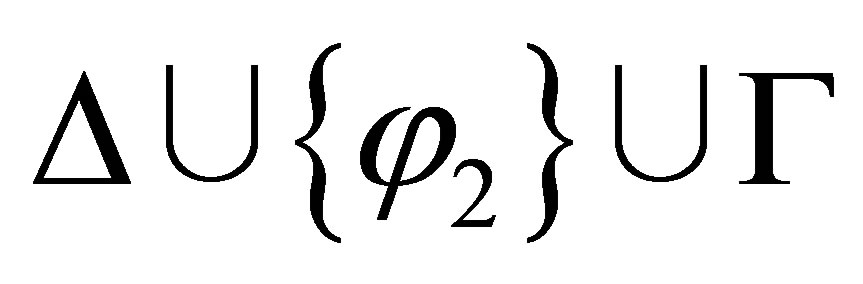 is consistent, and so is
is consistent, and so is 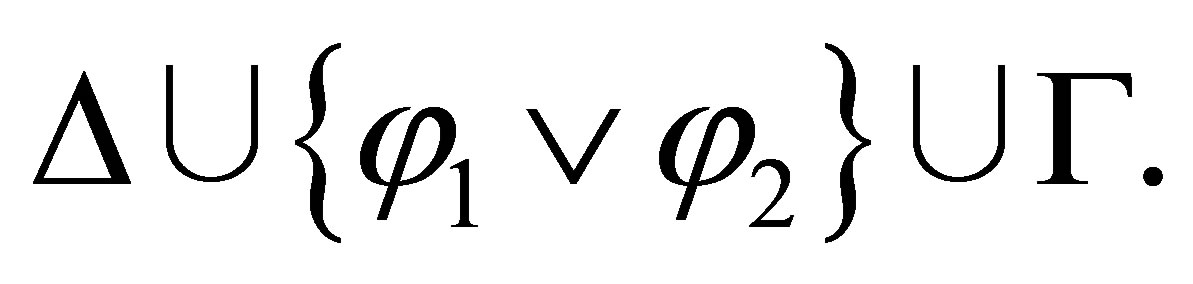
By the proof of the theorem, we have

Theorem 4.3. For any formula sets  and formula
and formula  if
if 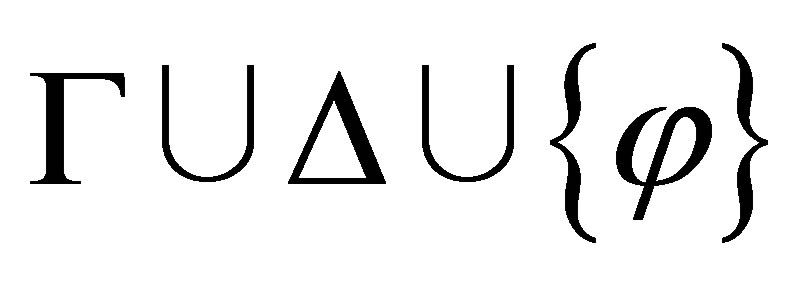 is consistent then
is consistent then 
Proof. We prove the theorem by the induction on the structure of 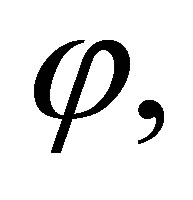 Assume that
Assume that 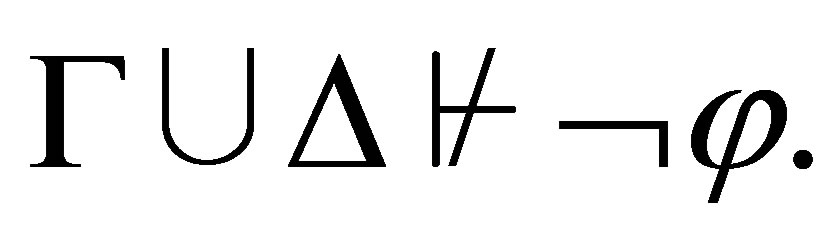
If 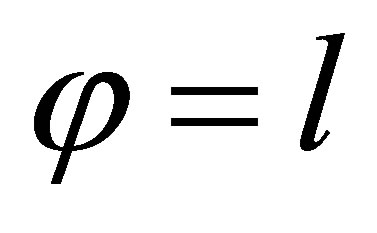 then
then  and
and 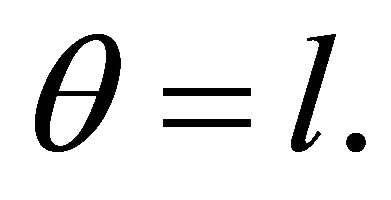 Hence,
Hence,

If 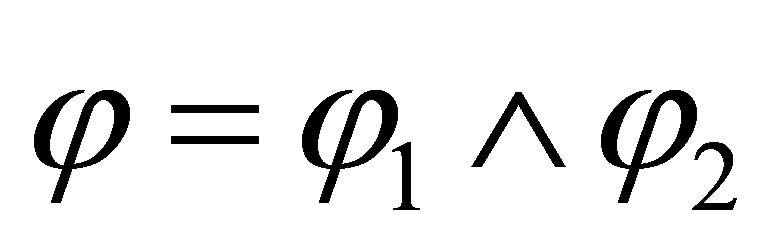 then
then  and
and 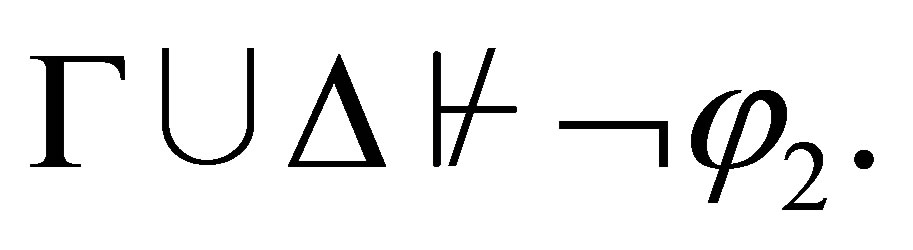 By the induction assumption,
By the induction assumption,


Hence, we have

If 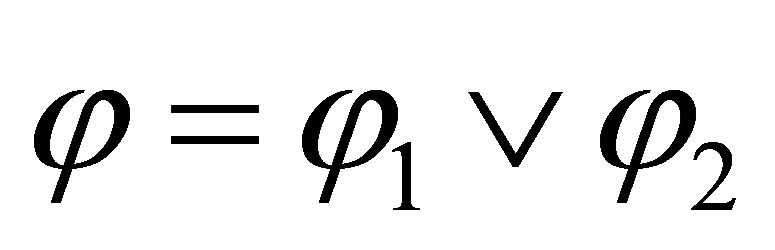 then either
then either  is consistent or
is consistent or 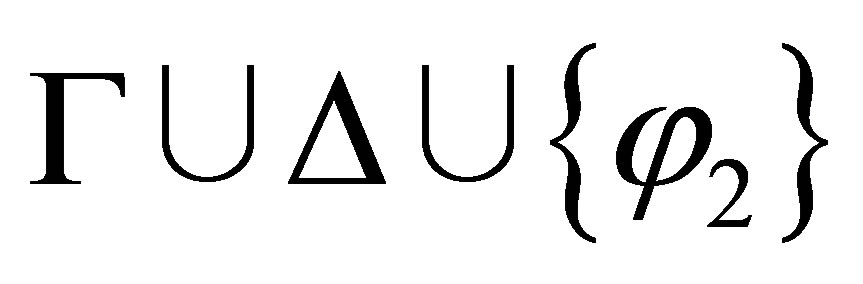 is consistent.
is consistent.
If 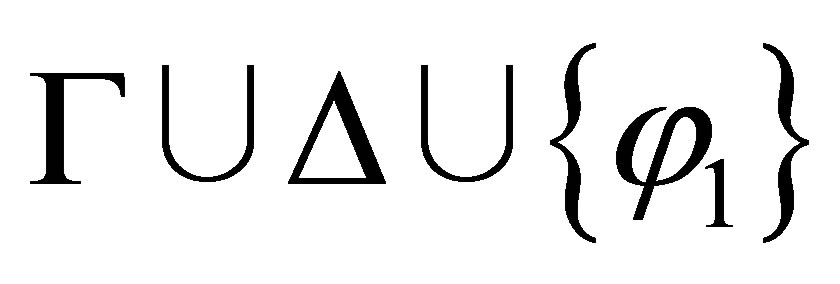 and
and 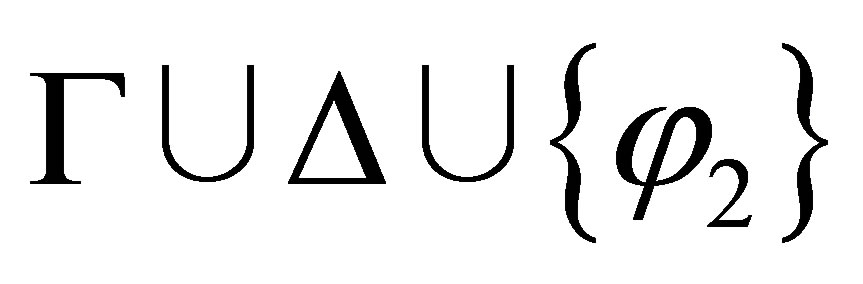 are consistent then
are consistent then 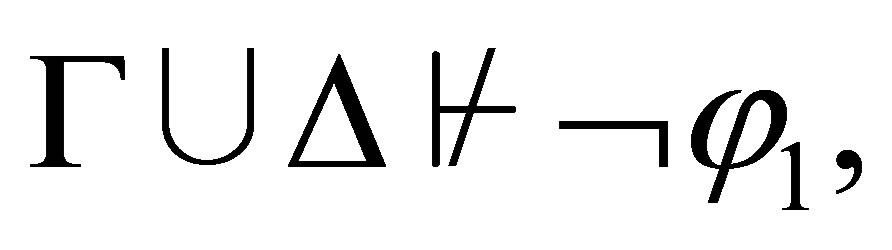 and
and 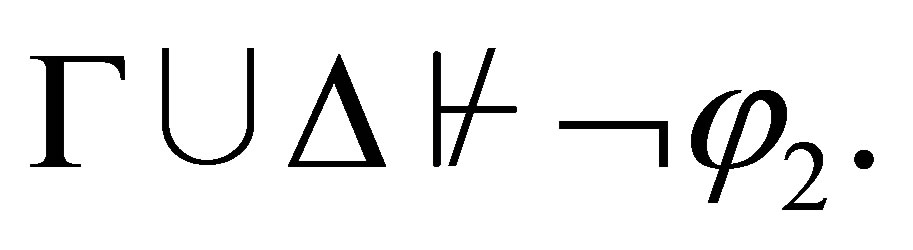 By the induction assumption,
By the induction assumption,


Hence, we have

If 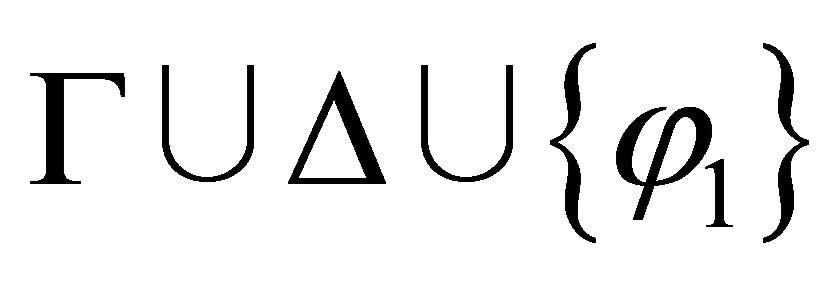 is inconsistent and
is inconsistent and 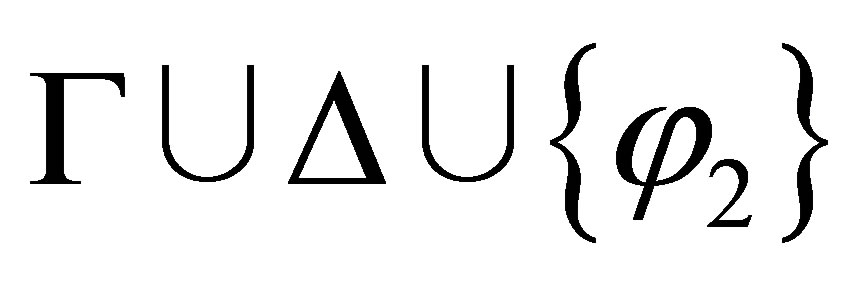 is consistent then
is consistent then 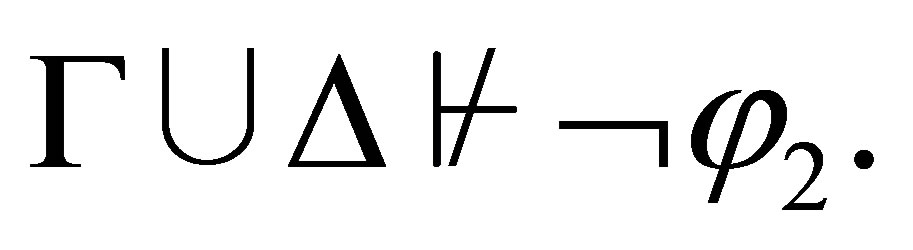 By the induction assumption,
By the induction assumption,  Hence, by Lemma 2.5, we have
Hence, by Lemma 2.5, we have
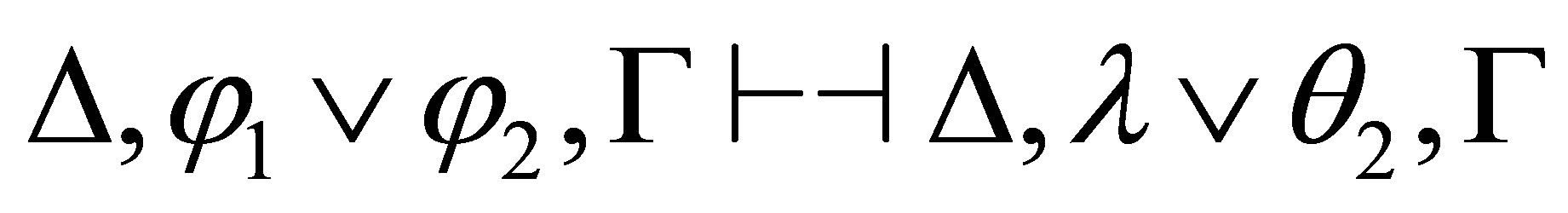
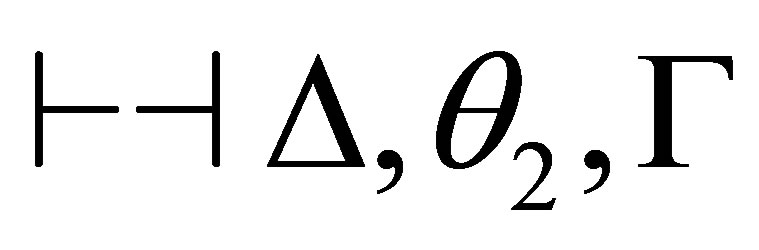


If 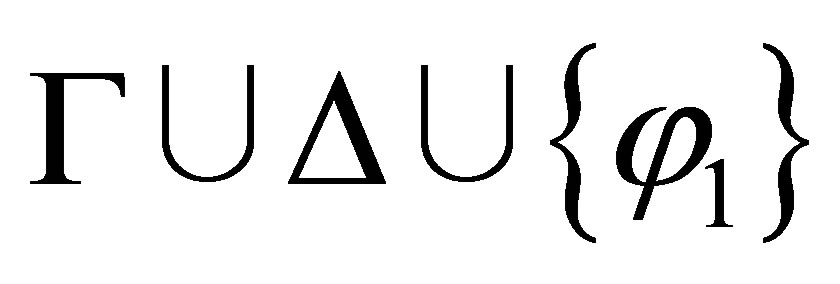 is consistent and
is consistent and 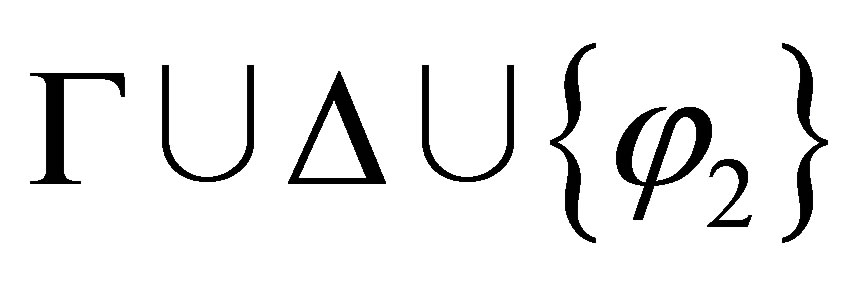 is inconsistent then
is inconsistent then 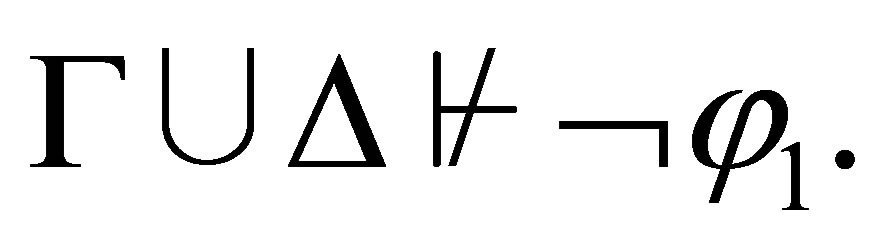 By the induction assumption,
By the induction assumption,  Hence, by Lemma 2.5, we have
Hence, by Lemma 2.5, we have
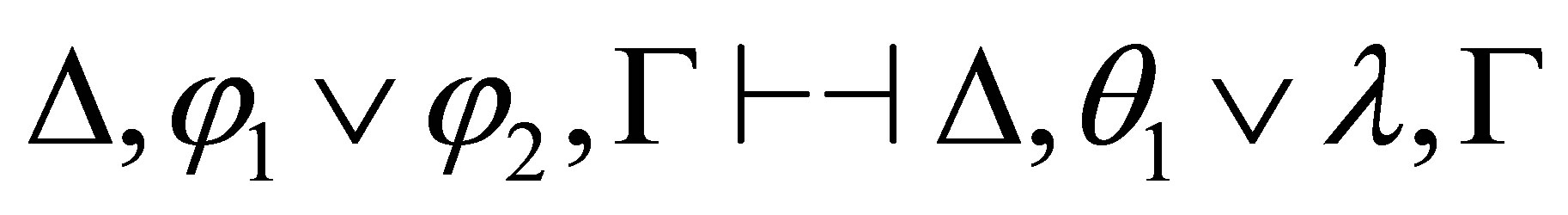
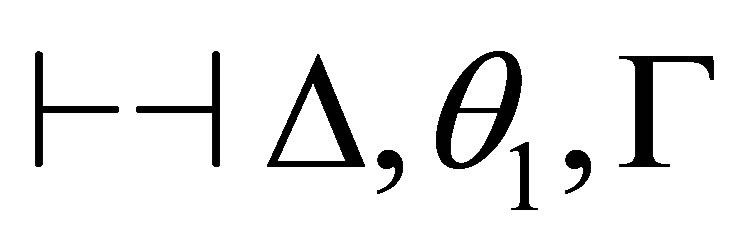
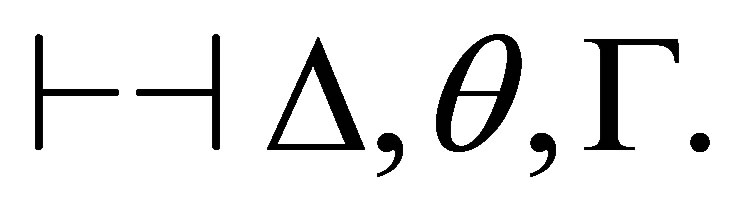
Theorem 4.4. For any consistent sets  of formulas and formula
of formulas and formula  if
if  is inconsistent then
is inconsistent then 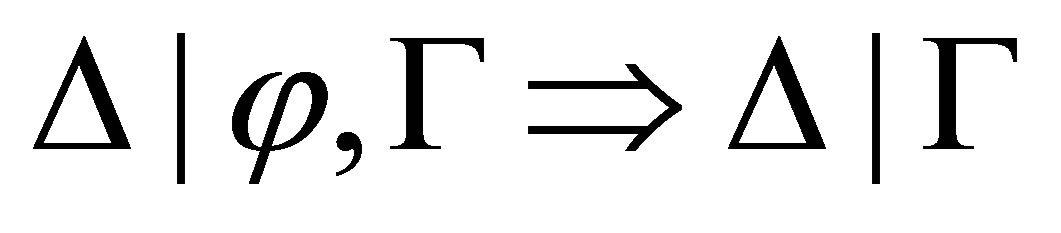 is provable; and if
is provable; and if  is consistent then there is a formula
is consistent then there is a formula  such that
such that 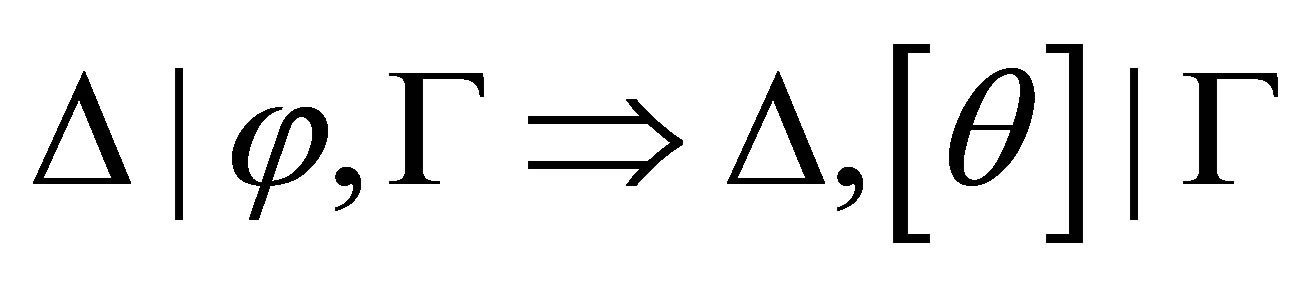 is provable.
is provable.
Proof. If  is inconsistent with
is inconsistent with  then similar to theorem 3.5,
then similar to theorem 3.5, 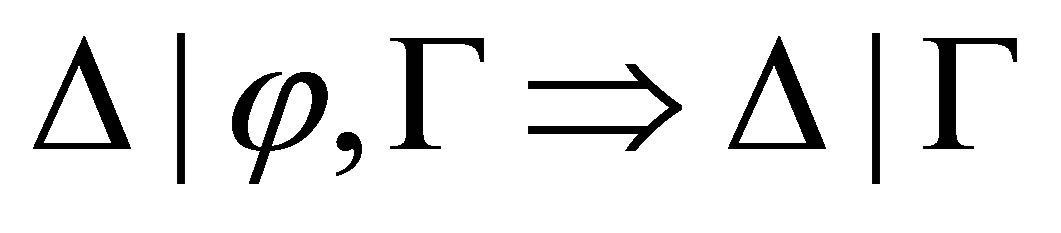 is provable.
is provable.
Assume that φ is consistent with 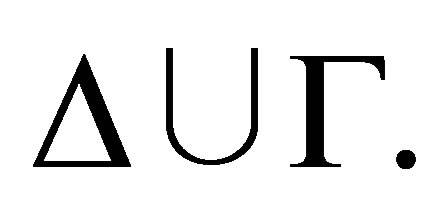 We prove the theorem by the induction on the structure of φ.
We prove the theorem by the induction on the structure of φ.
If φ = p then  and by
and by 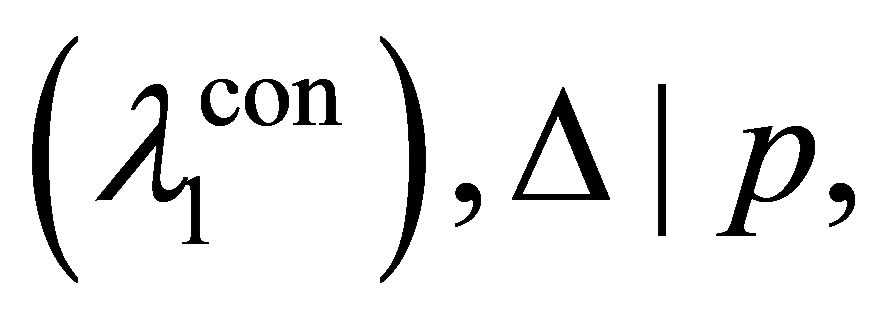
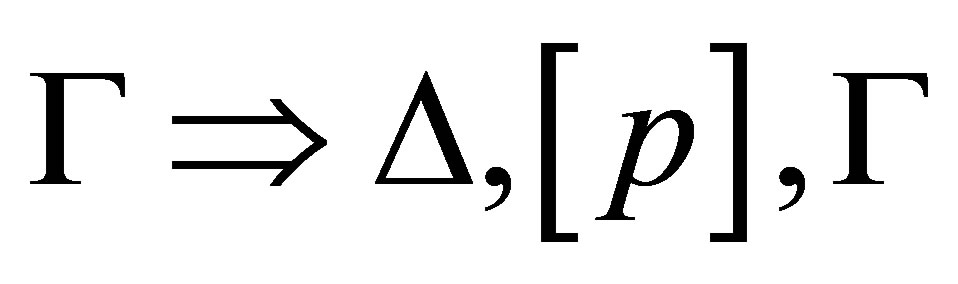 is provable, where
is provable, where 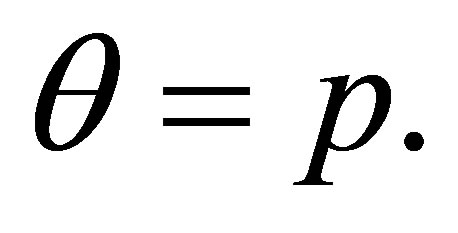
If 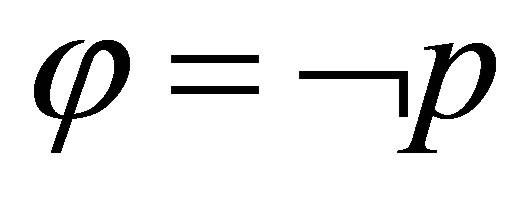 then
then 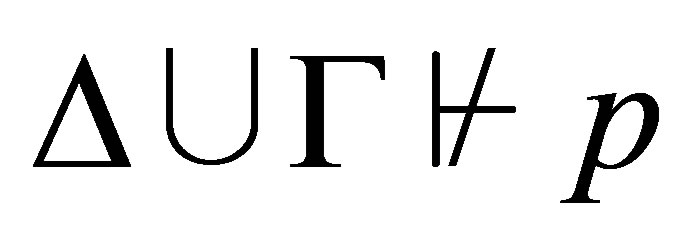 and by
and by 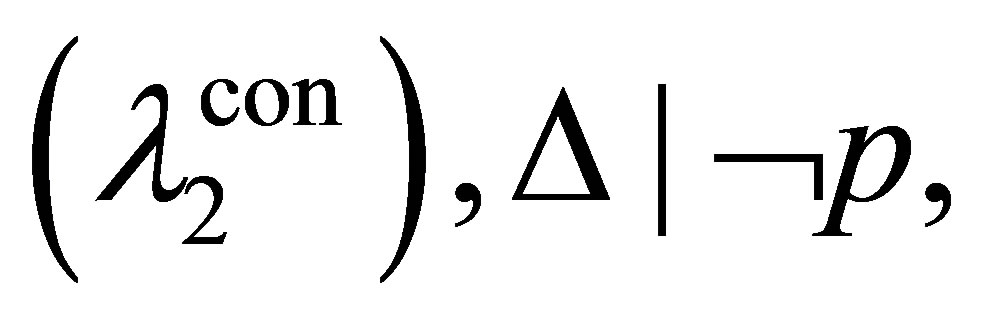
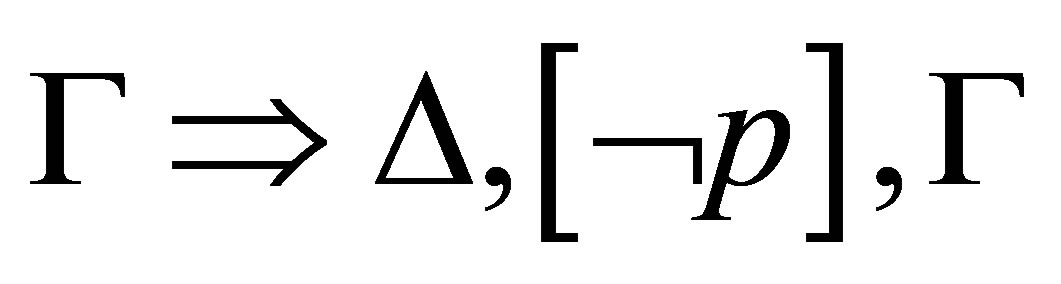 is provable, where
is provable, where 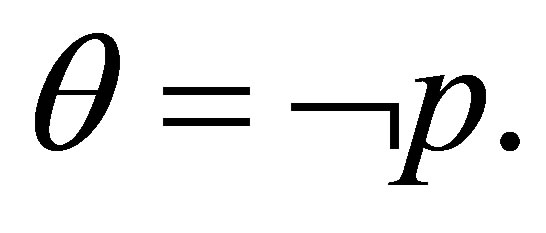
If 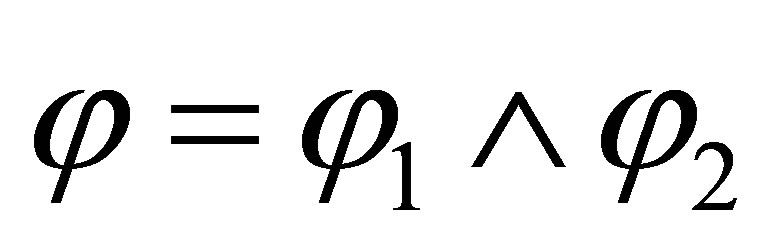 then φ1 is consistent with
then φ1 is consistent with  and φ2 is consistent with
and φ2 is consistent with 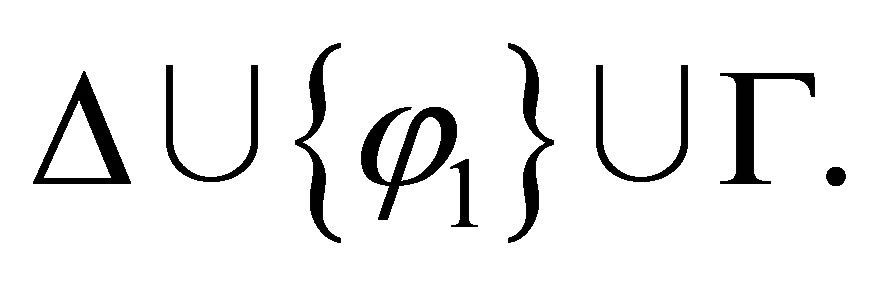 By the induction assumption, there are formulas
By the induction assumption, there are formulas  such that
such that 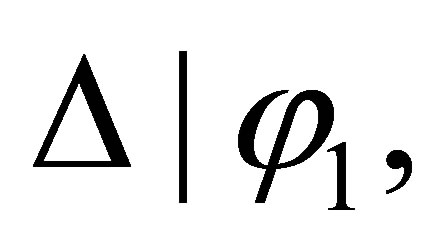
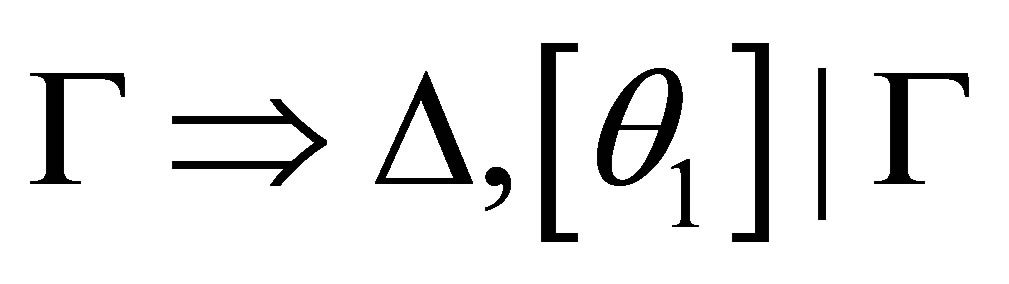 and
and 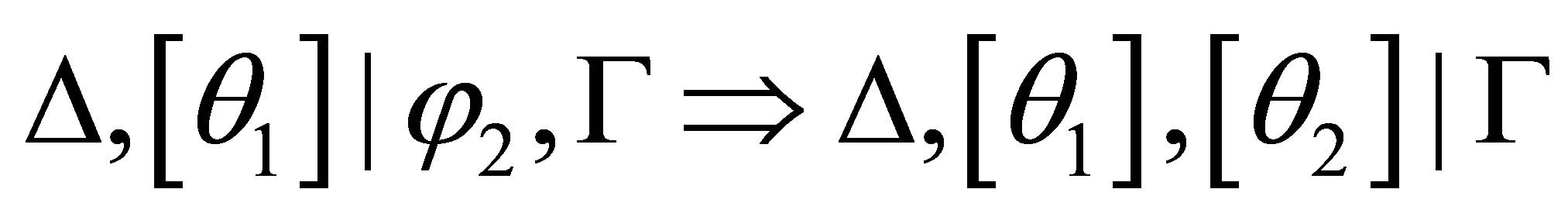 are provable. By
are provable. By 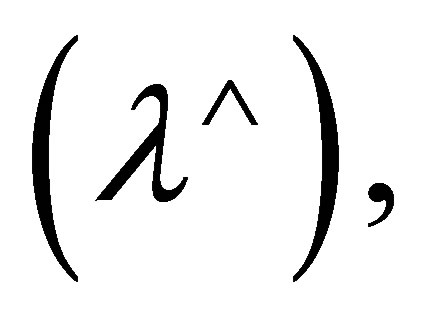 we have
we have
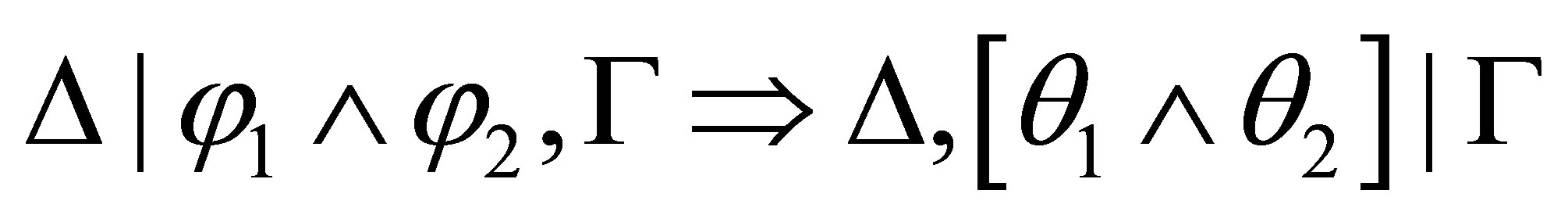
is provable, where 
If  then either
then either 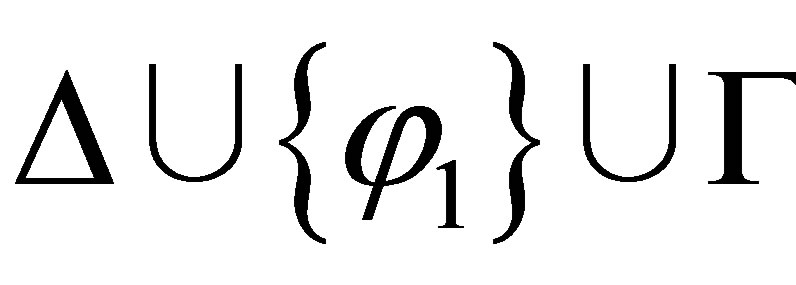 or
or 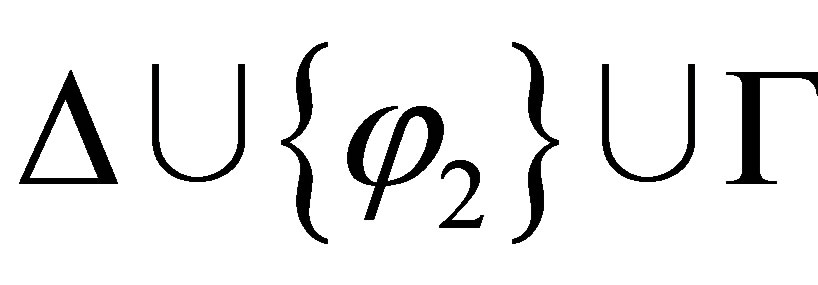 is consistent. By the induction assumption, if
is consistent. By the induction assumption, if 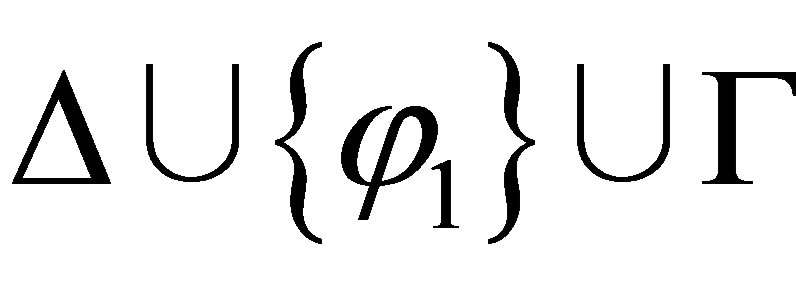 is consistent then there is a formula
is consistent then there is a formula 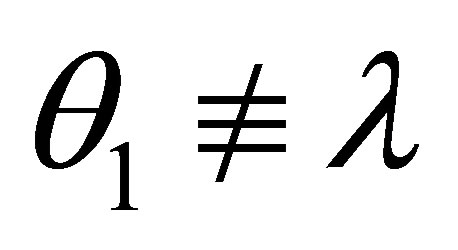 such that
such that  and if
and if 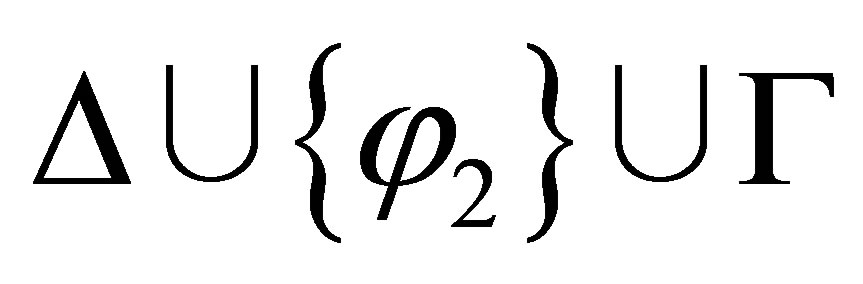 is consistent then there is a formula
is consistent then there is a formula 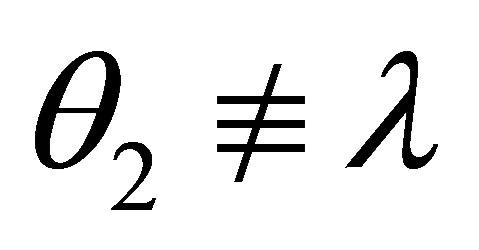 such that
such that 
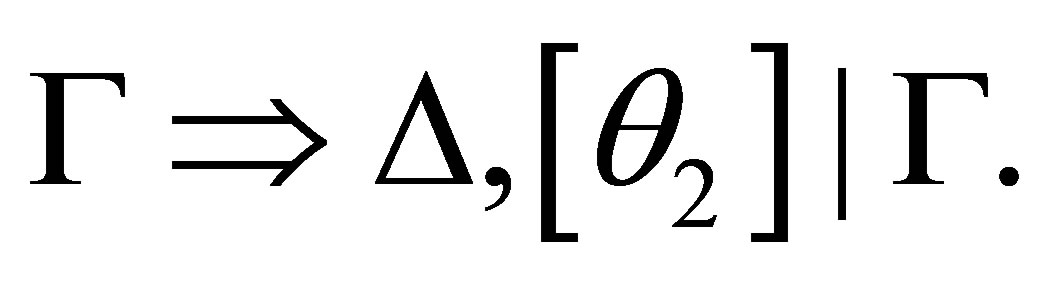 Then, by
Then, by 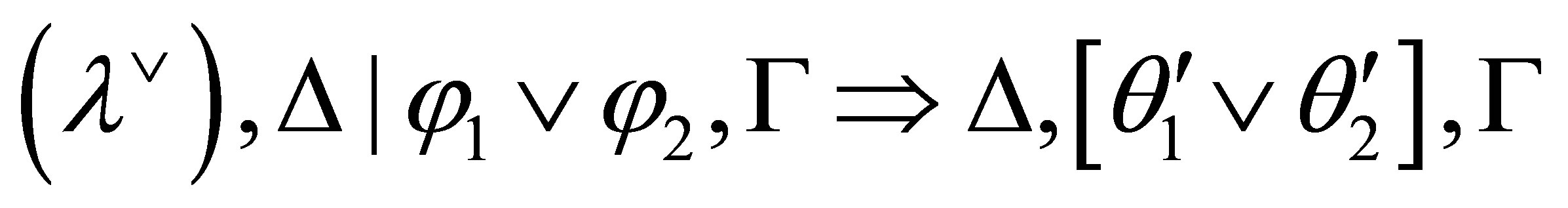 is provable, where
is provable, where

Remark. In fact, in theorem 4.3, if  is consistent then there is a formula
is consistent then there is a formula 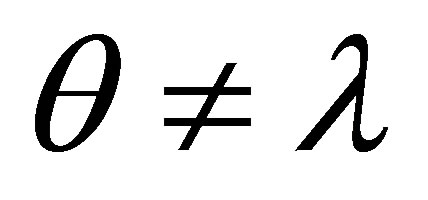 such that
such that 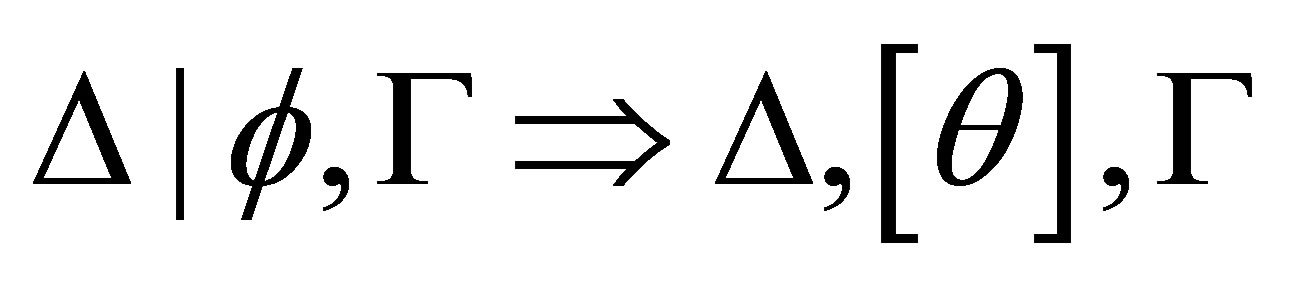 is provable.
is provable.
By Theorem 4.3, we have the following Theorem 4.5. (The soundness theorem for ). If
). If  is provable then
is provable then  is a pre-revision of
is a pre-revision of  by Δ.
by Δ.
Proof. We only prove that no subformula ξ of Ξ is contradictory to Δ.
Assume that there is a subformula ξ of some formula  in Ξ such that
in Ξ such that 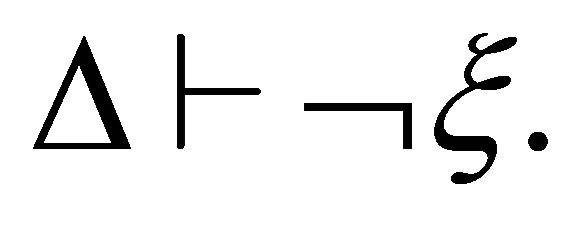 Let
Let 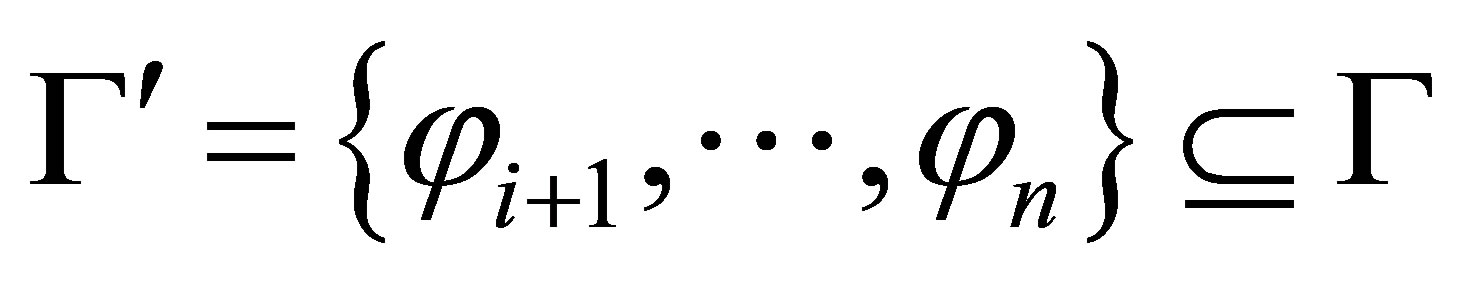 such that
such that 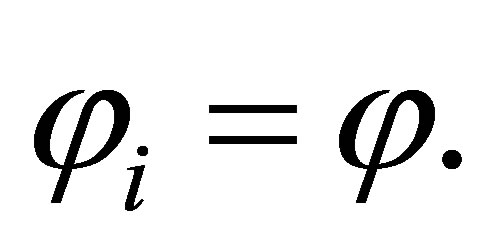
If  is inconsistent then
is inconsistent then 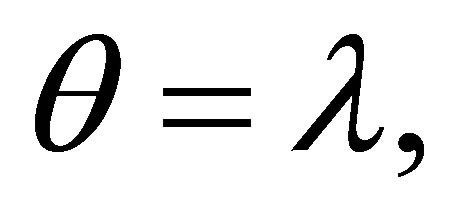 a contradiction.
a contradiction.
If 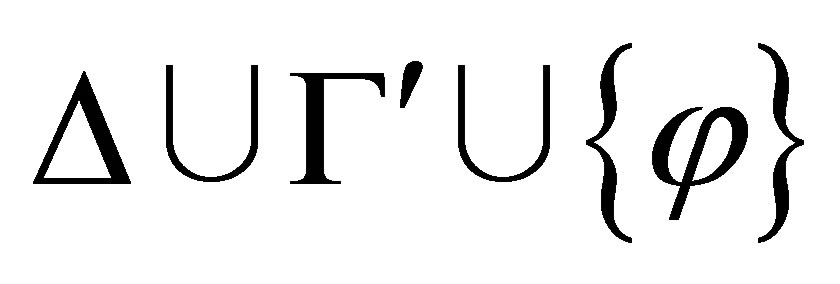 is consistent then by Lemma 3.5,
is consistent then by Lemma 3.5,

and for any subformula ξ of θ, if 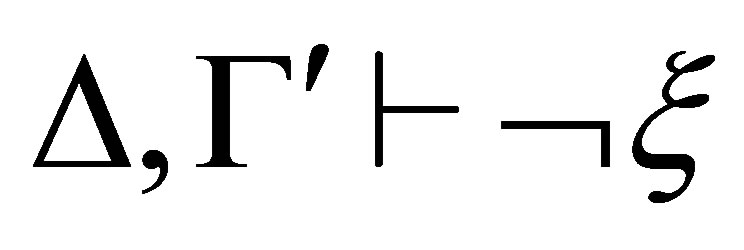 then, by the definition of θ, ξ is replaced by
then, by the definition of θ, ξ is replaced by  in θ, a contradiction to the assumption that ξ is a subformula of θ.
in θ, a contradiction to the assumption that ξ is a subformula of θ.
Theorem 4.6. (The completeness theorem for Γ). If Ξ is a pre-revision of Γ by Δ then 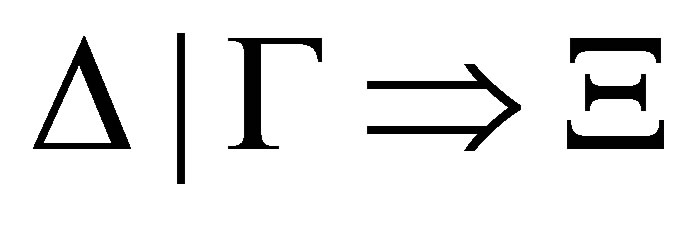 is provable.
is provable.
Proof. The proof is similar to theorem 3.7 and omitted.
5. Conclusion
This paper gave two  -calculi which are sound and complete with respect to the pseudo-revision and prerevision, respectively. The calculi are of Gentzen-type, in which each statement is of form
-calculi which are sound and complete with respect to the pseudo-revision and prerevision, respectively. The calculi are of Gentzen-type, in which each statement is of form 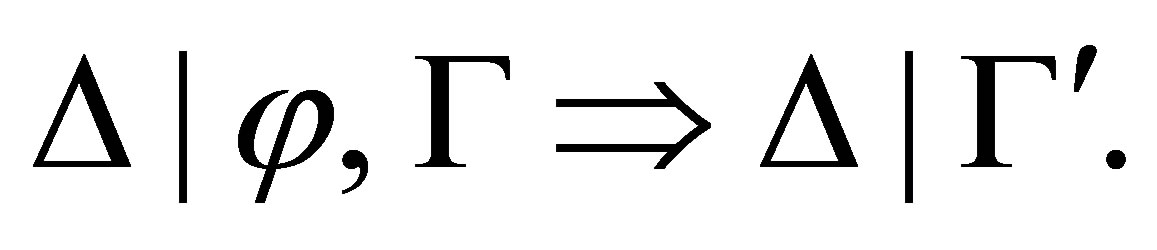 Different orderings of
Different orderings of  give different results of revision
give different results of revision 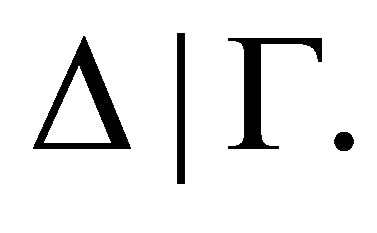 Correspondingly, if
Correspondingly, if 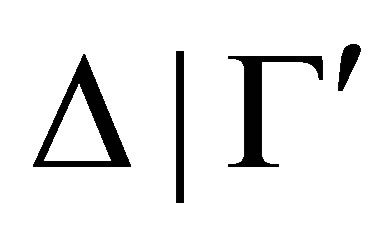 is irreducible, that is, no deduction rule can be used to reduce
is irreducible, that is, no deduction rule can be used to reduce 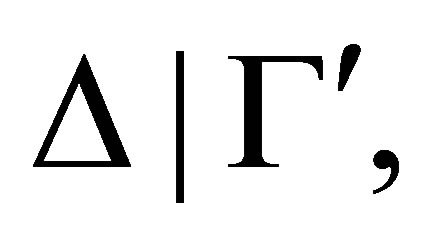 then
then 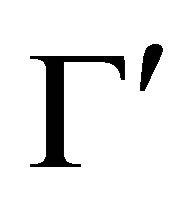 may be a minimal change of
may be a minimal change of 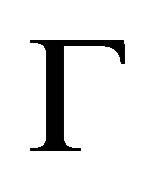 by
by  A further work is to give an
A further work is to give an 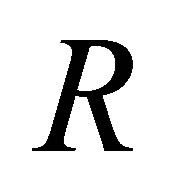 -calculus such that if
-calculus such that if  is irreducible then
is irreducible then  is consistent and
is consistent and 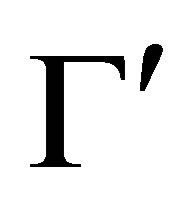 is a minimal change of
is a minimal change of  by
by  that is, for any
that is, for any 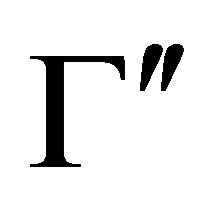 with
with  is inconsistent.
is inconsistent.
REFERENCES
- C. E. Alchourrón, P. Gärdenfors and D. Makinson, “On the Logic of Theory Change: Partial Meet Contraction and Revision Functions,” The Journal of Symbolic Logic, Vol. 50, No. 2, 1985, pp. 510-530. doi:10.2307/2274239
- A. Darwiche and J. Pearl, “On the Logic of Iterated Belief Revision,” Artificial Intelligence, Vol. 89, No. 1-2, 1997, pp. 1-29. doi:10.1016/S0004-3702(96)00038-0
- W. Li, “R-Calculus: An Inference System for Belief Revision,” The Computer Journal, Vol. 50, No. 4, 2007, pp. 378-390. doi:10.1093/comjnl/bxl069
- E. Fermé and S. O. Hansson, “AGM 25 Years, TwentyFive Years of Research in Belief Change,” Journal of Philosophical Logic, Vol. 40, No. 2, 2011, pp. 295-331. doi:10.1007/s10992-011-9171-9
- N. Friedman and J. Y. Halpern, “Belief Revision: A Critique, to Appear in J. of Logic, Language and Information,” In: L. C. Aiello, J. Doyle and S. C. Shapiro, Eds., Proceedings of the 5th Conference of Principles of Knowledge Representation and Reasoning, 1996, pp. 421-431.
- P. Gärdenfors and H. Rott, “Belief Revision,” In: D. M. Gabbay, C. J. Hogger and J. A. Robinson, Eds., Handbook of Logic in Artificial Intelligence and Logic Programming, Vol. 4, Epistemic and Temporal Reasoning, Oxford Science Pub., Oxford, 1995, pp. 35-132.
NOTES
*This work was supported by the Open Fund of the State Key Laboratory of Software Development Environment under Grant No. SKLSDE-2010KF-06, Beijing University of Aeronautics and Astronautics, and by the National Basic Research Program of China (973 Program) under Grant No. 2005CB321901.

