Open Journal of Modern Hydrology
Vol.06 No.02(2016), Article ID:66180,14 pages
10.4236/ojmh.2016.62009
A Diagnostic Approach towards the Causes of Energy Balance Closure Problem
Ali Varmaghani1, William E. Eichinger1, John H. Prueger2
1IIHR―Hydroscience & Engineering, University of Iowa, Iowa City, USA
2Agricultural Research Service, USDA, Ames, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 April 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
Hydrometeorological models are often evaluated and optimized on the basis of micrometeorological measurements. However, it has been known for more than three decades that surface measurements of sensible and latent heat energy (LE) are systematically underestimated. We studied this problem using six years of eddy-correlation measurements for four fields (corn, soybean, and prairie) in central Iowa, USA. We recorded major components of the energy equation (i.e. net radiation, sensible heat flux, LE, and soil heat flux, photosynthesis), and indirectly estimated most of the minor components of energy balance (namely storage in the soil, canopy and air). Storage in the canopy was related to leaf area index (LAI) acquired from Moderate Resolution Imaging Spectrometer (MODIS). In this paper, a diagnostic approach is investigated where systematic error is identified first. Three dimensional (3D) plots of the residual of energy equation vs. potential variables indicated the imbalance was largest mainly during the cold non-growing season when the soil was dry. Correlations between energy balance residual (EBR) and energy components showed that soil storage was not precisely estimated. Finally, an a-posteriori analysis (constrained linear multiple regression (CMLR)) was conducted to quantify the contribution of major/minor components of the energy equation towards EBR. The result highlights that the contribution of pertinent components of energy to EBR is mainly controlled by prevailing monthly hydrometeorological conditions; however, precise quantification of causes of imbalance is site-specific. A comparison between the a-posteriori analysis technique and the Bowen-ratio method demonstrates that the Bowen-ratio basically presumes a higher level of underestimation in LE. The results obtained in this study suggest that a-posteriori analysis may offer a superior methodology to correct measured eddy-correlation measurements. Furthermore, the overall trends in the correction of LE measurements suggest that there is a potential for rough monthly corrections of LE, irrespective of the type of crop.
Keywords:
Energy Balance Closure, Corn, Soybeans, Prairie, A-Posteriori Analysis

1. Introduction
Generally, researchers evaluate and optimize hydrological models on the basis of on-site micrometeorological measurements. As with all measurements, these are subject to uncertainty and what appears to be a systematic bias. We focus on the lack of closure in the energy equation (Equation (1)) at the surface―usually referred to as the surface energy balance closure (EBC) problem―which researches have noted for at least three decades:
 (1)
(1)
where Rn is net radiation, LE denotes latent heat flux, Hs represents sensible heat flux, and G is ground heat flux, all normally represented in [W∙m−2] [1] - [7] . The significance of the energy imbalance arises from the fact that the accuracy of a model is linked to the accuracy of its validation measurements. Global climate and regional models, to a great extent, are dependent upon the energy partitioning of the surface of the planet. The lack of closure impacts the methodologies used to estimate evapotranspiration (ET) as a residual of the energy balance equation. For example, ET estimation by satellite remote sensing relies on the assumption of energy balance [8] - [10] .
The practical applications of precise estimation of ET include irrigation scheduling, water conservation, global warming, and flood prediction, etc. [11] - [15] . To enhance the accuracy of the on-site quantification of Rn, G, and LE, researchers must also take into account elements that are routinely ignored because direct quantification of some energy terms such as storage or advection are data-intensive and cumbersome, or simply expensive, as in the case of storage in the soil, canopy, air, advection, and photosynthesis. To address the inaccuracies, latent and sensible heat fluxes by eddy-covariance measurements are customarily altered for closure by adjusting the fluxes while maintaining a constant ratio of Hs to LE (known as Bowen ratio) [16] . In spite of decades of research devoted to the factors contributing to energy imbalance, a unified approach to quantify the causes of lack of closure does not exist, in part because of the concerns mentioned above, and in part because contributing factors to energy imbalance may be site-specific or instrumentation-dependent [16] - [20] , and each field site is different.
Higgins [21] has recently suggested an a-posteriori analysis methodology which brings balance to the energy equation in a least-squares fashion. According to Higgins’ method, researches would attempt to quantify the contribution of the major/minor terms of the energy equation by means of Constrained Multiple Linear Regression (CMLR), which identifies the degree of responsibility of each process for lack of EBC. Even though Higgins indicated that a short period of analysis (roughly 6 days) would be sufficient for diagnosis, we will show that the contribution of some major components of energy in EBD varies over the course of a year, and the a-posteriori analysis must be conducted throughout the entire period. The objectives of this paper are to: (1) quantify and reduce any systematic error; (2) pinpoint the main sources of energy balance deficit (EBD) in a diagnostic way; (3) estimate the contribution of each term in the EBD according to a-posteriori analysis; and finally (4) attempt to relate EBC as a function of measurable covariates.
2. Micro-Meteorological Data
2.1. Site and Experiment Description
This work supports the Iowa Flood Center's (http://iowafloodcenter.org/) development of a flood warning system where spatially-resolved daily ET over Iowa is required by the model. Analysis of land cover Cropland Data Layer (CDL) maps provided by National Agricultural Statistics Service (NASS) shows that 80% of Iowa is covered by corn, soybeans, and prairie. These sites were as being typical of Iowa. Additionally, these sites are long term sites maintained by the USDA National Laboratory for Agriculture and Environment (NLAE) with high-quality, well-maintained equipment. NLAE, Ames, Iowa [22] provided the micro-meteorological data used in this study. Researchers recorded data for four agricultural fields quasi-continuously every 15 minutes since 2006, with minimal gaps due to field activities (i.e. planting), periodic calibrations, and sensor or data-logging problems. Table 1 reflects the geographical locations of the sites. Land cover code “Corn/Soybeans” indicates the annual rotation. Sites 1, 2, and 3 were adjacent farms. For our purposes, we focused on the time series between the years 2007-2012.
The data consisted of105 measured or derived variables (eddy-covariance fluxes, radiative fluxes, hydrometeorological data, covariance fluxes, soil properties, etc.). We computed turbulent fluxes of Hs, LE and momentum from the micrometeorological sensors using an eddy-covariance system operating at 20 Hz. Table 2 reflects the instrumentation utilized for recording these variables. The meteorological instruments were powered with deep cycle marine batteries connected to solar panels. All devices were wired to a Campbell Scientific CR3000 data logger. We buried two soil heat flux plates (SHFPs) at each site, one exactly below the vegetation row and
Table 1. Site location and site specification used in this study.
Table 2. Specification of the instrumentation used in the study.
au, v, and w are wind components; LE, Hs and SHF represent latent, sensible, and soil heat flux, respectively; Ta, Ts, and Tc denote air, surface, and above-canopy temperature, in order; RH stands for relative humidity; Rn is net radiation; SoilTC and Hydra_V represent soil temperature and probe’s voltage. bHeights varied typically year-by-year, site-by-site, and in summer/winter period, and are above-ground measurements. cDenotes measurements of same variable at different locations.
the other between the rows. The elevation of the SHFPs changed each year for different fields. We buried four soil thermocouples: two above each of the SHFPs were co-located and their elevation varied annually at 2, 4, and 6 cm below ground. Infrared Gas Analyzers (IRGAs) were open path sensors. The temperature-humidity sensors contained thin-film platinum resistance thermometers thermally attached to a capacitive relative humidity (RH) sensor.
2.2. Data Preparation, Filtering and Smoothing
Raw measurements from instruments may contain erroneous data and need to be refined in a secondary process before application. We imported the data into MATLAB®, and eliminated outliers and suspicious values based on our suggested lower/upper thresholds specific for each variable, recorded in Table 3. Spikes were removed by using a 2-dimensional (2D) MATLAB filter (i.e. lnfilter: general sliding-neighborhood operations) which applies a given function, usually an average function, to each m-by-n sliding block of the variable matrix. In Table 3 we set the filter parameters for each variable, set based on engineering judgment.
We visually checked the data, and removed corrupted records by means of MATLAB graphically interactive functions. In some periods, soil heat flux at one field had an abnormal reverse pattern. We believe that the operator incorrectly wired the plate. The RH during some periods was not recorded; the data was recovered from vapor density and air temperature [23] . Even though we could have performed data smoothing according to the procedure outlined in [24] , fluctuations in patterns of different variables seemed to be natural. In sum, a total of roughly 200,000 records for each variable were left for analysis.
3. Methodology
In this section, first attempts are made to estimate the contribution of minor components of energy balance equation. Some of the components are directly computed from the field measurements, and the rest (i.e. heat storage in the canopy, and advection) are indirectly estimated. Then, we try to pinpoint and measure any systematic error according to the scatterplots of the residual of energy vs. independent variables. Further, this helps to identify any imprecise estimation of energy balance equation components on the basis of any visible trend. The next step is devoted to pointing out the location and reason of high residual based on three-dimensional (3D) plots of residual of energy equation vs. potential covariates. Finally, an a-posteriori analysis (constrained linear multiple regression (CMLR)) will be performed to bring balance to the energy equation and quantify the contribution of major/minor components of the equation.
Table 3. Suggested thresholds and filter settings used for raw data refinement.
aV stands for variable and F represent the response of filter function. *Denotes different measurements of same variable at different locations.
3.1. Estimation of Energy Balance Minor Components
There are three primary causes for energy imbalance: measurement errors, the nonidentical elevations of these measurements, and the elimination of “insignificant” components contributing to the energy equation [1] .
The first type of error is attributed to measurement errors. The expected measurement errors associated with the instrumentation in this study include: the accuracy of the CSAT3 anemometer for Hs and LE, the K&Z CMP 21 Pyranometer error, IRPT-P3 infrared sensor measurement errors, soil temperature measurement errors, air temperature measurements errors, and CO2 concentration measurement errors. The accuracy of the CSAT3 anemometer for Hs and LE is 10% or 10 W/m2, and 10% or 20 W/m2, respectively [25] , which is considered to be high-class (class 1 - 3 according to [26] ). The K&Z CMP 21 Pyranometer error is less than 10 W/m2 for an estimation of Rn [27] . It should be noted that, to date, no argument exists to show that Rn is overestimated [1] . Shortwave measurement cannot be assumed to be more accurate than 2% [28] . 5% error is expected in HFT-3.1 SHFP [29] . The IRPT-P3 infrared sensor measures surface and above canopy temperature with an accuracy of 0.3˚C [30] . Campbell Scientific [31] reports soil temperature measurements by 107-L soil thermocouple to be inaccurate by 0.4˚C. Air temperature accuracy ranges from 0.2˚C to 0.4˚C for the HMP45C temperature probe [32] . The LI-COR 7500 has an absolute accuracy of 1% in CO2 concentration [33] .
The second type of error refers to the fact that the measurements of the main energy components (i.e. Rn, Hs, LE, & G) are not made at the same location (see Table 2). The location of the footprint of turbulent fluxes is dislocated from the measurement site and may be significantly impacted by the interaction between the height of measurements and atmosphere stability [34] . Ground heat flux is usually measured a few centimeters below the surface, which ignores the storage term between the measurement plate and the surface. The storage term has been significant in some cases [35] [36] .
The third type of error comes from ignoring what many consider “inconsequential” terms in the energy balance equation, thus relying upon an inaccurate equation (i.e. Equation (1)). Terms that researchers generally presumed negligible may turn out to be significant under certain circumstances, such as storage terms [37] - [40] , or the advection term [41] [42] . Even though storage terms and photosynthesis are typically ignored, the data showed that these terms can contribute between 1% and 16% of net radiation which is confirmed by [43] . A more complete form of the energy balance equation [44] can, therefore, be written as:
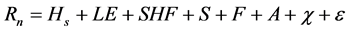 (2)
(2)
where S represents heat storage in the canopy, and F denotes photosynthesis where CO2 flux is used as an indicator. SHF stands for Soil Heat Flux at the plate; given the fact that plates are buried in the ground, some energy is always stored between the plate and surface (Sg), and ground heat flux (G) will be calculated from algebraic summation of SHF and Sg. A is the advection term, ε represents systematic measurement errors, and c is other terms which include mismatched measurement footprints, freeze/thaw in a snowpack, and soil water transport, etc. [21] .
In order to better analyze contributing factors to the energy imbalance, we estimated the non-measured components of Equation (2). The first component is the storage term, partitioned into three components: heat storage in the soil (Sg), the air (Sa), and the canopy (Sc). The first part of storage term, Sg, heat storage in the soil has turned out to be a significant factor in the accurate estimation of ground heat flux [43] [45] . In the flux experiment, we located SHFPs at 6 - 10 cm, and embedded two temperature sensors in the soil, one at 2 cm depth and the second sensor at between 4 and 8 cm in different fields each year. Soil moisture analog hydra probes’ depths were at 5cm; these probes measured four voltages at four levels, which were converted to soil water content (θ) and conductivity (σs) by means of the free program “hyd_file_2.8.exe” [46] . We took into account the effect of soil moisture in soil heat storage computations where the two temperatures were extrapolated for at-surface and top plate temperatures:
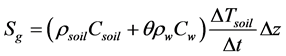 (3)
(3)
where ρsoil and ρw are soil bulk and water density, respectively; Csoil and Cw are, in order, specific heat capacity of mineral soil and water; ΔTsoil denotes temperature difference between at-surface and top plate; Δt is time step; and Δz is the depth of SHF plate [43] .
The second part of storage occurs in the canopy. We estimated the rate change in the enthalpy of the canopy within each 15-minute time interval (Sc) from temperature gradient and available water/biomass:
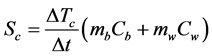 (4)
(4)
where Tc represents canopy temperature, and Cb is specific heat capacity of biomass in the plant. The nomenclature mw and mb represent water and biomass content in the canopy, respectively, and can be quantified by plant destruction. In the absence of such destruction, we related the aforementioned parameters to Leaf Area Index (LAI) on the basis of the curves presented by Meyers and Hollinger [43] :
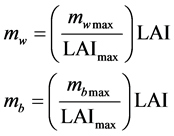 (5)
(5)
where the values of parameters are suggested in Table 4. We interpolated the LAI of the sites, both spatially and temporally, from the 4-Day 1 km LAI, MCD15A3 product retrieved from the Moderate Resolution Imaging Spectroradiometer (MODIS).
Table 4. Recommended values for the parameters in Equation (5).
In addition to energy storage in the soil and canopy, heat energy is stored in the air. We quantified the heat storage in the air (Sa) in the sense that we took into account the effect of specific humidity levels [47] [48] :
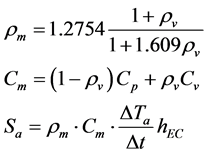 (6)
(6)
In the equations above, ρm and ρv represent moist air and water vapor density, respectively; Cm, Cp and Cv denote, in order, specific heat capacity of moist air, air, and water vapor at constant pressure; Ta is air temperature; and hEC is the height of the eddy covariance instrument below which the energy is stored in the air.
The next term in Equation (2) is photosynthesis, F. We converted CO2 fluxes to photosynthesis by Lp, thermal conversion factor for fixation of CO2 [44] . The fifth term of Equation (2), advection, A, is difficult to accurately quantify, and requires numerous measurements at different locations of the EBC control volume [42] . Detailed data of the type needed to estimate A were not available. Therefore, we measured/estimated only the first five terms of the right-hand side of Equation (2), and used them to plot the daily-averaged residual of energy (Figure 1). The curves in Figure 1 demonstrate the same seasonal trends, and the energy equation suffers most from imbalance in February and March when snowmelt may play a significant role.
Since quantification of advection requires numerous instruments, Higgins [21] suggests an indirect estimation of advection where advection (A) can be represented as a function of mean wind velocity (u), wind direction (θu), and Monin-Obukhov length (L):
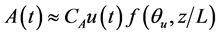 (7)
(7)
where f is an unknown function of wind direction and atmospheric stability, z/L. CA represents adjusting factor, and z denotes measurement height. The Monin-Obukhov length is generally used as an indicator of atmosphere stability (L < 0, L = 0, and L > 0, respectively for unstable, neutral, and stable phase), and can be represented as a function of friction velocity, latent, and sensible heat flux:
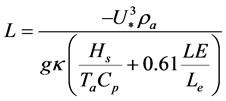 (8)
(8)
Figure 1. Daily-averaged residual of Equation (2), analyzed based on observations of different land covers ignoring the terms A and c.
where U* is fiction velocity; ρa denotes density of air; and g, κ, and Le represents acceleration due to gravity, Von-Karman constant, and latent heat of vaporization, respectively [44] . Since f is a periodic function (θu = θu + 360˚), a second degree Taylor expansion of Equation (7) can be written as:
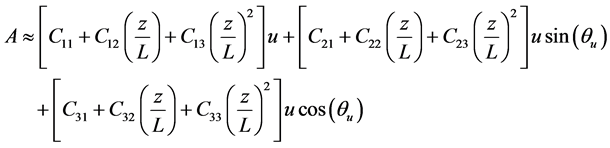 (9)
(9)
where Cij are unknown coefficients.
3.2. Diagnosis of the Causes of Energy Imbalance
Figure 1 from the previous section indicated a significant residual of 50 W∙m−2 which is equivalent to an ET of 1.8 mm∙day−1. Under these circumstances, the natural course of action would be to analyze the residual in order to figure out the contribution of each covariate in the residual. Figure 2 demonstrates the variation of residual of energy vs. potential covariates for all atmospheric conditions. The horizontal blue curves indicate the moving average, and each error bar corresponds to the standard deviation of each variable over the local range. The Monin-Obukhov lengths with absolute values greater than 2000 were set to ±2000. The subplots indicate that there is roughly a linear relation between RES and Rn, Sg, Sc, and Ta. Due to the multicollinearity and cross-interaction between the variables, it is not feasible to clearly distinguish linear/nonlinear relationships between the residual and the independent variable. In case of any linear relation, CMLR is able to cope with the issue.




Figure 2. Variation of residual (RES) of energy in [Wm-2] vs. potential variables. The horizontal blue curves indicate the moving average. Each error bar corresponds to the standard deviation of each coefficientover the local range. (a) Rn [W/m2]; (b) LE [W/m2]; (c) H [W/m2]; (d) SHFP [W/m2]; (e) L [m]; (f) ustar [m/s]; (g) dirU [Deg.]; (h) Ta [˚C]; (i) Sa [W/m2]; (j) Sc [W/m2]; (k) Sg [W/m2]; (l) F [W/m2]; (m) P [kPa]; (n) LAI [-]; (o) tw [days]; (p) RAIN [mm/15 min].
Subplot (k) suggests that Sg is not precisely estimated. Although this may be due to the assumption of a linear soil temperature profile, estimation of Sg using an exponential profile [49] exacerbated the estimation by an increase of 54% in Sg. The homogenous distribution of residual in subplots (g), (o), and (p) imply: (1) the residual cannot be attributed to wind direction or rainfall; and (2) a systematic error of ~19 W m-2 is detectable from the mentioned plots. We eliminated the systematic error before the a-posteriori analysis.
To better pinpoint the location of the significant residuals, we generated 3-dimensional (3D) plots of residual vs. potential covariates. Figure 3 depicts a series of graphs where noticeable residual (RES) is demonstrated as a function of two covariates. In the figure, ETo denotes reference evapotranspiration computed from [50] . Graphs (a - d) indicate that maximum RES occurs in fairly no evaporating condition. Additionally, RES suffers most in cold weather (i.e. Ta < 5˚C) over bare soil, resembling a sunny cold day when Rn is relatively high and the atmosphere is at near-neutral stable condition. It can be concluded that LE cannot be the salient cause of the residual; rather, the snowmelt can lead to significant residuals, particularly when the Monin-Obukhov length is zero. This is confirmed by [51] where snowmelt initiation depends heavily upon an air temperature near freezing and low wind velocity.
3.3. A-Posteriori Analysis
We conducted an a-posteriori analysis to identify the individual contributions to the residual. This type of a- posteriori analysis, suggested by Higgins [21] , attempts to decompose the residual by adjusting coefficients to the components of Equation (2) through CMLR. Applying the coefficients Ci and inserting Equation (8) into Equation (2) yields:



Figure 3. 3D plots of residual of energy eqation vs. potential covariates. The colored surface represents residual [W∙m−2]. (a) Ta [˚C]; (b) LE [W/m2]; (c) Rn [W/m2]; (d) Ta [˚C].
where a total of 17 coefficients must be determined. Higgins recommends that an a-posteriori analysis be conducted separately for different stability conditions [21] . Since we wanted to focus on the accurate quantification of latent heat flux, we conducted our analysis only for unstable atmospheric condition. Setting realistic upper/lower bounds for the balancing coefficients can facilitate CMLR. For instance, uncertainty in Rn can be limited to 4% according to the instrument specification. Coefficients for fluxes, storage terms, and photosynthesis are positive. Advection terms can be positive or negative as described by Kochendorfer and Paw [42] . We performed an individual a-posteriori analysis for each crop at each year with a sliding block of ten days to observe the dynamics of the residual throughout the year. We determined the unknown coefficients of Equation (9) through CMLR (“lsqlin” function in MATLABTM). Figure 4 reflects the variation of the coefficients throughout the year for all sites and all years.
As our study shows, Rn is overestimated during the growing season. Even though there could be at most 4% uncertainty in Rn, no arguments can be found in the literature to prove that the net radiation is overestimated [52] . The subplots (a - b) indicate that Hs and LE are systematically underestimated; however, during the growing season, the eddy-covariance towers better estimate Hs and LE. Peculiarly, we observed that there is approximately 15% overestimation of LE during August at the peak of the growing season, which may be attributed to overestimating Rn during the aforementioned period. The plots indicate significant underestimation of LE during the non-growing season; this is, however, not generally a matter of concern since LE is small during the winter. Similar to Higgins [21] , who found advection to be a statistically insignificant term, subplots (i - q) of the coefficients of the advection terms (see Equation (8)) indicate a small contribution of advection to the residual. Typically, horizontal advection between the canopy top and the measurement height of eddy-covariance flux could account for as much as 10% of the imbalance in the energy budget [6] . Subplot (r) is the “offset” of the CMLR, which is close to zero during the growing season. Random offset still exists during the winter, which could be indicative of a missed variable in Equation (9), such as freeze/thaw in a snowpack.
The micrometeorological data explored in this paper are meant to be exploited for evaluation of an evapotranspiration model implemented by the authors, and hence, precise quantification of latent heat flux is the primary motivation of this study. Therefore, in order to evaluate the response of each site against an a-posteriori



Figure 4. Variation of the coefficients of Equation (9) throughout the year, obtained from an a-posteriori analysis, as an average for all sites and years. The coefficients are a moving average of each 10 days. DOY stands for the “day of year”. (a) - (r): DOY.
analysis, we performed the technique separately for each site, each year, and vectors of balancing coefficients, for a total of 18 parameters (shown in Figure 4), were estimated throughout the year.
Figure 5 compares latent heat balancing coefficients for each site, each year. The figure shows the dynamics of the LE coefficient for different crops during the year. Since we estimated the coefficients as the average of each 10-day sliding block, the last coefficient belongs to DOYs of 356-366. Subplot (a) shows that the behavior of all three crops is similar, particularly during the growing season. During the cold non-growing season, we observed several similar jumps, which may be indicative of snow precipitation/melting. The general trend of balancing the coefficient for all three crops might suggest that the dynamics of energy imbalance is controlled by prevailing hydrometeorological conditions. This may propose a potential method for a rough correction of fluxes as a function of day-of-year. Subplot (b) demonstrates the variation of the balancing coefficient only for corn fields, which indicates that the precise correction of fluxes is complex and site-specific.
4. Discussion and Conclusion
As previously mentioned, the Monin-Obukhov length, L, is a measure of atmospheric stability (L< 0, L = 0, and L > 0 represent stable, neutral, and unstable phase, respectively). The dimensionless stability parameter, z/L, is also widely used in parallel with Monin-Obukhov length, where z is the height of hydrometeorological measurements. The term z/L is zero at statically neutral conditions, and it is positive (negative) in a typical range of 1 to 5 (−5 to −1) for stable (unstable) stratification [53] . Franssen et al. [54] show that the relative residual (RES/Rn) increases as the stability parameter approaches zero (i.e. very stable/unstable atmosphere); however, Figure 6 depicts the distribution of residual of energy vs the Monin-Obukhov length for the entire dataset. As Figure 6 demonstrates, the largest residuals occur when L tends toward zero. Equation (8) helps explain this: usually at dawn and dusk, a neutral condition governs, and L is expected to be zero since U* approaches zero; simultaneously, since LE is negligible, Hs experiences a smooth transition from negative to positive at dawn and vice versa at dusk. This will result in the denominator of the equation approaching zero, which leads L to be positive/negative infinity.
One of the most serious concerns of energy imbalance lies in latent heat flux measurements. Latent heat flux plays a key role in mesoscale models, and its precise quantification has been a challenging issue for decades [1] . As previously mentioned, energy balance is customarily forced by adjusting LE and Hs while maintaining the Bowen ratio. Therefore, we compared the adjusted LEs using the Bowen-ratio method and the a-posteriori analysis technique. Figure 7 is a scatter plot of 100,000 randomly-selected observations. As can be inferred, the plot suggests that the Bowen-ratio method underestimates latent heat flux measurements more so than an a-posteriori analysis approach. There are very few sporadic circumstances observable in Figure 7 where the a-posteriori

Figure 5. (a) Variation of latent heat balancing coefficient (CLE) for corn, soybean, and prairie throughout the year, computed from an a-posteriroi analysis. DOY stands for “day of year”. Each curve is the average of all CLE for each land cover for the entire dataset; (b) Variation of latent heat balancing coefficient (CLE) for eachcorn field seperatelywhere merely the growing season is magnified. Legend:“SiYj” stands for the site i, at the year j. (a) DOY; (b) DOY.
Figure 6. Variation of residual (RES) of energy in [W∙m−2] vs. Monin-obukhov length, L for all fields.
Figure 7. Adjusted latent heat flux 15-min site measurements for 100,000 randomly- selected observations: a comparison between a-posteriori analysis and Bowen-ratio method.
analysis approach has increased LE more than the Bowen ratio method. Unexpectedly, the upper bound of the Bowen ratio method is in a linear relationship with the a-posteriori analysis technique, implying that the Bowen- ratio method, at its highest level, can adjust latent heat flux up to 2.6 times when compared with the a-posteriori analysis. In consideration of the range of LE balancing coefficient obtained during evaporative season, this might suggest that the Bowen-ratio method [16] unrealistically adjusts latent heat flux while the maximum expected uncertainty associated with eddy-covariance instruments is 20% [25] . Interestingly, the intercept of the asymptote is equal to the systematic error discovered in section 3.2.
In this paper, we attempted to identify and correct the root causes of lack of energy closure in three agricultural fields. We found that the energy equation suffered most from imbalance during the cold non-growing season. This might strongly be attributed to freeze/thaw in a snowpack, as confirmed by Hoffman et al. [51] . For future research, we recommend that the height of snow and ice conditions also be recorded. Scatter plots of potential covariates vs independent variables showed that there was a systematic error of 19 W m-2, which could be immediately eliminated. Using the technique suggested by Higgins [21] , we conducted an a-posteriori analysis (CMLR) to quantify the contribution of each variable to the lack of energy closure. Even though Higgins suggests that data analysis for a short period of one week is sufficient, Figure 4 shows that the contribution of each covariate varies throughout the year, and the process is mainly driven by prevailing hydrometeorological conditions. The dynamics of the sensible heat balancing coefficient during the growing season resembles LAI even though the instrument specification limits the error of net radiation to 4%. Figure 4 shows that there may exist greater overestimation in net radiation during the growing season. Even though quantification of all of the components of the energy equation was not feasible, the significance of advection terms was indirectly investigated. In line with Higgins’ findings [21] , the impact of advection on energy imbalance is minimal. Storage in the soil was not precisely estimated and we corrected this through a-posteriori analyses. The overall trend in Figure 5 might suggest that there is a potential for correcting the latent and sensible heat fluxes according to monthly governing hydrometeorological conditions; however, in consideration of the trend for each field, precise quantification of latent heat flux is still site-specific.
Acknowledgements
This work was accomplished under the grant support of Iowa Flood Center (IFC). We are grateful to the USDA National Laboratory for Agriculture and Environment, Ames, IA for providing the micrometeorological data. The MCD15A3 was retrieved from the online Data Pool, courtesy of the NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota, https://lpdaac.usgs.gov/data_access/data_pool. We also express our appreciation to the anonymous reviewers for their constructive remarks.
Cite this paper
Ali Varmaghani,William E. Eichinger,John H. Prueger, (2016) A Diagnostic Approach towards the Causes of Energy Balance Closure Problem. Open Journal of Modern Hydrology,06,101-114. doi: 10.4236/ojmh.2016.62009
References
- 1. Foken, T. (2008) The Energy Balance Closure Problem: An Overview. Ecological Applications, 18, 1351-1367.
http://dx.doi.org/10.1890/06-0922.1 - 2. Foken, T., Aubinet, M., Finnigan, J.J., Leclerc, M.Y., Mauder, M. and Paw, U.K.T. (2011) Results of a Panel Discussion about the Energy Balance Closure Correction for Trace Gases. Bulletin of the American Meteorological Society, 92, ES13-ES18.
http://dx.doi.org/10.1175/2011BAMS3130.1 - 3. Foken, T., Mauder, M., Liebethal, C., Wimmer, F., Beyrich, F., Leps, J.-P., Raasch, S., DeBruin, H.A., Meijninger, W.M. and Bange, J. (2010) Energy Balance Closure for the LITFASS-2003 Experiment. Theoretical and Applied Climatology, 101, 149-160.
http://dx.doi.org/10.1007/s00704-009-0216-8 - 4. Kidston, J., Brümmer, C., Black, T.A., Morgenstern, K., Nesic, Z., McCaughey, J.H. and Barr, A.G. (2010) Energy Balance Closure Using Eddy Covariance above Two Different Land Surfaces and Implications for CO2 Flux Measurements. Boundary-Layer Meteorology, 136, 193-218.
http://dx.doi.org/10.1007/s10546-010-9507-y - 5. Leuning, R., Van Gorsel, E., Massman, W.J. and Isaac, P.R. (2012) Reflections on the Surface Energy Imbalance Problem. Agricultural and Forest Meteorology, 156, 65-74.
http://dx.doi.org/10.1016/j.agrformet.2011.12.002 - 6. Oncley, S.P., Foken, T., Vogt, R., Kohsiek, W., DeBruin, H., Bernhofer, C., Christen, A., van Gorsel, E., Grantz, D. and Feigenwinter, C. (2007) The Energy Balance Experiment EBEX-2000. Part I: Overview and Energy Balance. Boundary-Layer Meteorology, 123, 1-28.
http://dx.doi.org/10.1007/s10546-007-9161-1 - 7. Wilson, K., Goldstein, A., Falge, E., Aubinet, M., Baldocchi, D., Berbigier, P., Bernhofer, C., Ceulemans, R., Dolman, H. and Field, C. (2002) Energy Balance Closure at FLUXNET Sites. Agricultural and Forest Meteorology, 113, 223-243.
http://dx.doi.org/10.1016/S0168-1923(02)00109-0 - 8. Allen, R.G., Tasumi, M. and Trezza, R. (2007) Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. Journal of Irrigation and Drainage Engineering, 133, 380-394.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2007)133:4(395) - 9. Compaoré, H., Hendrickx, J.M., Hong, S.-H., Friesen, J., van de Giesen, N.C., Rodgers, C., Szarzynski, J. and Vlek, P. L. (2008) Evaporation Mapping at Two Scales Using Optical Imagery in the White Volta Basin, Upper East Ghana. Physics and Chemistry of the Earth, Parts A/B/C, 33, 127-140.
http://dx.doi.org/10.1016/j.pce.2007.04.021 - 10. Long, D. and Singh, V.P. (2010) Integration of the GG Model with SEBAL to Produce Time Series of Evapotranspiration of High Spatial Resolution at Watershed Scales. Journal of Geophysical Research: Atmospheres (1984-2012), 115, No. D21.
http://dx.doi.org/10.1029/2010JD014092 - 11. Alley, W.M. (1984) On the Treatment of Evapotranspiration, Soil Moisture Accounting, and Aquifer Recharge in Monthly Water Balance Models. Water Resources Research, 20, 1137-1149.
http://dx.doi.org/10.1029/WR020i008p01137 - 12. Jensen, M., Wright, J. and Pratt, B. (1971) Estimating Soil Moisture Depletion from Climate, Crop and Soil Data. Transactions of the ASAE, 14, 954-959.
http://dx.doi.org/10.13031/2013.38430 - 13. Narasimhan, B., Srinivasan, R., Arnold, J. and Di Luzio, M. (2005) Estimation of Long-Term Soil Moisture Using a Distributed Parameter Hydrologic Model and Verification Using Remotely Sensed Data. Transactions of the ASAE, 48, 1101-1113.
http://dx.doi.org/10.13031/2013.18520 - 14. Nicholson, S.E., Marengo, J., Kim, J., Lare, A.R., Galle, S. and Kerr, Y.H. (1997) A Daily Resolution Evapoclimatonomy Model Applied to Surface Water Balance Calculations at the HAPEX-Sahel Supersites. Journal of Hydrology, 188, 946-964.
http://dx.doi.org/10.1016/S0022-1694(96)03178-2 - 15. Umair, S.M. and Usman, R. (2010) Automation of Irrigation System Using ANN Based Controller. International Journal of Electrical & Computer Sciences IJECS-IJENS, 10, 41-47.
- 16. Twine, T.E., Kustas, W.P., Norman, J.M., Cook, D.R., Houser, P., Meyers, T.P., Prueger, J.H., Starks, P.J. and Wesely, M.L. (2000) Correcting Eddy-Covariance Flux Underestimates over a Grassland. Agricultural and Forest Meteorology, 103, 279-300.
http://dx.doi.org/10.1016/S0168-1923(00)00123-4 - 17. Barr, A.G., Morgenstern, K., Black, T.A., McCaughey, J.H. and Nesic, Z. (2006) Surface Energy Balance Closure by the Eddy-Covariance Method above Three Boreal Forest Stands and Implications for the Measurement of the CO2 Flux. Agricultural and Forest Meteorology, 140, 322-337.
http://dx.doi.org/10.1016/j.agrformet.2006.08.007 - 18. Ingwersen, J., Hogy, P., Fangmeier, A. and Streck, T. (2012) Energy Balance Closure Methods of Eddy Covariance Data Tested by a Coupled Land Surface-Crop Growth Model. EGU General Assembly Conference Abstracts, 14, EGU2012-7316.
- 19. Massman, W. and Lee, X. (2002) Eddy Covariance Flux Corrections and Uncertainties in Long-Term Studies of Carbon and Energy Exchanges. Agricultural and Forest Meteorology, 113, 121-144.
http://dx.doi.org/10.1016/S0168-1923(02)00105-3 - 20. Panin, G.N., Tetzlaff, G. and Raabe, A. (1998) Inhomogeneity of the Land Surface and Problems in the Parameterization of Surface Fluxes in Natural Conditions. Theoretical and Applied Climatology, 60, 163-178.
http://dx.doi.org/10.1007/s007040050041 - 21. Higgins, C.W. (2012) A-Posteriori Analysis of Surface Energy Budget Closure to Determine Missed Energy Pathways. Geophysical Research Letters, 39, L19403.
http://dx.doi.org/10.1029/2012GL052918 - 22. ARS (2015) National Laboratory for Agriculture and the Environment. Agricultural Research Service, USDA.
http://www.ars.usda.gov/main/site_main.htm?modecode=50-30-15-00 - 23. Haynes, W.M. (2013) CRC Handbook of Chemistry and Physics. 44th Edition, Chemical Rubber Company (CRC) Press, Cleveland, 2544.
- 24. Hojstrup, J. (1993) A Statistical Data Screening Procedure. Measurement Science and Technology, 4, 153-157.
http://dx.doi.org/10.1088/0957-0233/4/2/003 - 25. Mauder, M., Liebethal, C., Gockede, M., Leps, J.-P., Beyrich, F. and Foken, T. (2006) Processing and Quality Control of Flux Data during LITFASS-2003. Boundary-Layer Meteorology, 121, 67-88.
http://dx.doi.org/10.1007/s10546-006-9094-0 - 26. Foken, T., Goockede, M., Mauder, M., Mahrt, L., Amiro, B. and Munger, W. (2005) Post-Field Data Quality Control. In: Lee, X., Massman, W.J. and Law, B. Eds., Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis, Springer, Dordrecht, 181-208.
http://dx.doi.org/10.1007/1-4020-2265-4_9 - 27. Kipp & Zonen (2015) CMP21 Pyranometer Specification. Kipp & Zonen B.V.
http://www.kippzonen.com/Product/14/CMP-21-Pyranometer#.VbLu4kZ1Y9Y - 28. Brock, F.V. and Richardson, S.J. (2001) Meteorological Measurement Systems. Vol. 86, Oxford University Press, New York, 100.
- 29. CS (2012) Model 107 Temperature Probe. Revision: 5/12. Campbell Scientific, Inc.
https://s.campbellsci.com/documents/af/manuals/107.pdf - 30. Apogee (2015) Infrared Radiometers. Apogee Instruments, Inc.
http://www.apogeeinstruments.com/infraredradiometer/ - 31. CS (1999) HFT3 Soil Heat Flux Plate. Revision: 2/99. Campbell Scientific, Inc.
http://www.eol.ucar.edu/rtf/facilities/isff/sensors/rebs/hft.pdf - 32. CS (2009) Model HMP45C Temperature and Relative Humidity Probe. Revision: 3/09. Campbell Scientific, Inc.
https://s.campbellsci.com/documents/us/manuals/hmp45c.pdf - 33. LI-COR (2015) LI-7500A Calibration. LI-COR, Inc.
http://www.licor.com/env/products/gas_analysis/LI-7500A/calibration.html - 34. Schmid, H. (1997) Experimental Design for Flux Measurements: Matching Scales of Observations and Fluxes. Agricultural and Forest Meteorology, 87, 179-200.
http://dx.doi.org/10.1016/S0168-1923(97)00011-7 - 35. Liebethal, C., Huwe, B. and Foken, T. (2005) Sensitivity Analysis for Two Ground Heat Flux Calculation Approaches. Agricultural and Forest Meteorology, 132, 253-262.
http://dx.doi.org/10.1016/j.agrformet.2005.08.001 - 36. Mayocchi, C. and Bristow, K.L. (1995) Soil Surface Heat Flux: Some General Questions and Comments on Measurements. Agricultural and Forest Meteorology, 75, 43-50.
http://dx.doi.org/10.1016/0168-1923(94)02198-S - 37. Jacobs, A.F., Heusinkveld, B.G. and Holtslag, A.A. (2008) Towards Closing the Surface Energy Budget of a Mid-Latitude Grassland. Boundary-Layer Meteorology, 126, 125-136.
http://dx.doi.org/10.1007/s10546-007-9209-2 - 38. Lindroth, A., Molder, M. and Lagergren, F. (2010) Heat Storage in Forest Biomass Improves Energy Balance Closure. Biogeosciences, 7, 301-313.
http://dx.doi.org/10.5194/bg-7-301-2010 - 39. Moderow, U., Aubinet, M., Feigenwinter, C., Kolle, O., Lindroth, A., Molder, M., Montagnani, L., Rebmann, C. and Bernhofer, C. (2009) Available Energy and Energy Balance Closure at Four Coniferous Forest Sites across Europe. Theoretical and Applied Climatology, 98, 397-412.
http://dx.doi.org/10.1007/s00704-009-0175-0 - 40. Oliphant, A., Grimmond, C., Zutter, H., Schmid, H., Su, H.-B., Scott, S., Offerle, B., Randolph, J. and Ehman, J. (2004) Heat Storage and Energy Balance Fluxes for a Temperate Deciduous Forest. Agricultural and Forest Meteorology, 126, 185-201.
http://dx.doi.org/10.1016/j.agrformet.2004.07.003 - 41. Aubinet, M., Feigenwinter, C., Heinesch, B., Bernhofer, C., Canepa, E., Lindroth, A., Montagnani, L., Rebmann, C., Sedlak, P. and Van Gorsel, E. (2010) Direct Advection Measurements Do not Help to Solve the Night-Time CO2 Closure Problem: Evidence from Three Different Forests. Agricultural and Forest Meteorology, 150, 655-664.
http://dx.doi.org/10.1016/j.agrformet.2010.01.016 - 42. Kochendorfer, J. and Paw, U.K.T. (2011) Field Estimates of Scalar Advection across a Canopy Edge. Agricultural and Forest Meteorology, 151, 585-594.
http://dx.doi.org/10.1016/j.agrformet.2011.01.003 - 43. Meyers, T.P. and Hollinger, S.E. (2004) An Assessment of Storage Terms in the Surface Energy Balance of Maize and Soybean. Agricultural and Forest Meteorology, 125, 105-115.
http://dx.doi.org/10.1016/j.agrformet.2004.03.001 - 44. Brutsaert, W. (1982) Evaporation into the Atmosphere: Theory, History, and Applications. Springer, Dordrecht, 299.
http://dx.doi.org/10.1007/978-94-017-1497-6 - 45. Heusinkveld, B., Jacobs, A., Holtslag, A. and Berkowicz, S. (2004) Surface Energy Balance Closure in an Arid Region: Role of Soil Heat Flux. Agricultural and Forest Meteorology, 122, 21-37.
http://dx.doi.org/10.1016/j.agrformet.2003.09.005 - 46. Stevens (2015) HYD_FILE.EXE for Analog Hydra Probe (Version 2.8) [Computer Program].
https://stevens.zendesk.com/hc/en-us/articles/216056387-HydraProbe-AKA-Hydra-Probe-II-and-HydraProbe-Analog - 47. The Engineering ToolBox (2014) Density of Dry Air, Water Vapor and Moist Humid Air. The Engineering ToolBox.
http://www.engineeringtoolbox.com/density-air-d_680.html - 48. Ambaum, M.H. (2010) Thermal Physics of the Atmosphere. Vol. 1, John Wiley & Sons, Noida, India, 109.
- 49. Kusuda, T. and Achenbach, P.R. (1965) Earth Temperature and Thermal Diffusivity at Selected Stations in the United States. DTIC Document.
- 50. FAO (2015) Chapter 4—Determination of ETo. Food and Agriculture Organization of the United Nations.
http://www.fao.org/docrep/x0490e/x0490e08.htm - 51. Hoffman, M.J., Fountain, A.G. and Liston, G.E. (2008) Surface Energy Balance and Melt Thresholds over 11 Years at Taylor Glacier, Antarctica. Journal of Geophysical Research: Earth Surface (2003-2012), 113, F04014.
- 52. Foken, T. (1998) Die Scheinbar Ungeschlossene Energiebilanz am Erdboden—Eine Herausforderung an Die Experimentelle Meteorologie. Sitzungsberichte der Leibniz-Sozietat, 24, 131-150.
- 53. AMS (2012) Obukhov Length. American Meteorological Society.
http://glossary.ametsoc.org/wiki/Obukhov_length - 54. Franssen, H.H., Stockli, R., Lehner, I., Rotenberg, E. and Seneviratne, S. (2010) Energy Balance Closure of Eddy- Covariance Data: A Multisite Analysis for European FLUXNET Stations. Agricultural and Forest Meteorology, 150, 1553-1567.
http://dx.doi.org/10.1016/j.agrformet.2010.08.005





