Open Journal of Acoustics
Vol.05 No.03(2015), Article ID:59687,9 pages
10.4236/oja.2015.53010
To the Question of Sound Waves Propagation in Liquid
V. P. Ivanov, G. K. Ivanova
Institute of Applied Physics, Russian Academy of Sciences, Nizhny Novgorod, Russia
Email: ivg@hydro.appl.sci-nnov.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2015; accepted 14 September 2015; published 17 September 2015
ABSTRACT
This paper is proposed to consider the propagation of sound waves in the liquid as a result of special deformation of the medium. Mechanical vibrations of the membrane, (diaphragm) creating a sound wave, transfer from layer to layer in medium without causing synchronous oscillations of the fluid particles. It can be assumed that the deformation of the liquid is similar to the driving force (pressure) in the direction perpendicular to the plane of the vibrating membrane. Usually, the running wave functions are used to describe the sound waves, but they do not contain the direction of propagation. It is proposed to consider that the amplitude of the wave is a vector coinciding with the vector tangent to the path of the wave. This would allow for a change of direction of propagation without changing its phase, in which the direction of wave is not present. It proposed a method of calculating a vector of amplitudes of the reflected and transmitted sound waves based on the laws of conservation of impulse and energy of the waves and the boundary conditions defined by Snell’s law. It is shown that one of the two solutions of the wave equation does not apply to real physical process of sound wave’s propagation in the liquid.
Keywords:
Sound Running Waves, Wave Equation, Reflection, Passage, Liquid Space

1. Introduction
Propagation of sound waves in the liquid has one character feature which is fixed in numerous experiments. There is time (frequency) dependence invariability of acoustic wave in process of propagation [1] . In a limited frequency range and at the absence of absorption effect, the influence the space on the sound wave is practically absent, just keeping its “temporary portrait”. The role of the space is reduced to sending the temporary membrane vibration at the observation point in time which is determined by the velocity of propagation of a sound wave in the liquid. It is found out thoroughly that, what is the mechanism of propagation of sound in the liquid is not possible at this time. A similar situation is observed in the propagation of electromagnetic (EM) waves in a vacuum. Only the velocity of propagation and preservation of the spectral composition of EM waves are known. Due to the experimental study of the interaction of electromagnetic waves with matter there were written equations (Maxwell’s equations) establishing interaction of EM waves with any medium. The same equations with the corresponding parameters of the medium describe the propagation of EM waves in vacuum.
Acoustics to describe the propagation of waves in the liquid Euler and continuity of the space equations is used. Since the results of any interaction of sound waves with the environment (and their influence on each other) are not known, in order to receive mentioned equations, the specific mechanism has been proposed for the interaction of sound and environment. Based on this mechanism and under certain conditions, Euler and the continuity of the medium equations are used to describe the propagation of sound waves in the liquid. It was decided that the sound wave vibrations cause the particles of liquid and pressure with the sound wave frequency. The pressure in the liquid changes in the small amount compared with the pressure in the absence of waves [2] -[4] .
The purpose of this work is to analyze the possibility to use the Euler equations and the equation of continuity to the description of the propagation of sound waves in a fluid. As a result it suggests an alternative mechanism of sound propagation. It is the mechanism of deformation of liquid, consisting in the transmission of the pressure wave from one layer to the layer adjacent to it. This type of deformation allows the possibility of movement of the wave in the space without knowledge of the specific forms of interaction of the sound wave and liquid. The introduction of the mechanism of deformation layer by layer allows to use the running sound wave for the description of sound propagation with the speed that is determined by the liquid. Based on that form of deformation, a new method is offered for calculating amplitudes (coefficients) of the reflected and transmitted waves. New in this method is the use of vector addition of sound waves whose amplitudes are invited to consider the vectors. Two conservation laws are used―the law of conservation of impulse (the speed with a mass equal to one) and the law of conservation of energy of the sound wave. Vector’s direction of the reflected and transmitted waves is determined by the Snell’s law as in the other studies.
2. Euler Equations and Continuity. The Mechanism of Deformation and Propagation of Sound Waves in Liquid
In papers on hydrodynamics, see, for example, [2] -[4] , the liquid is considered as a continuous medium. Every small element of this medium has the same properties as the whole liquid, but consists of a large number of molecules. The mathematical description of the liquid is usually carried out using Euler’s equations and continuity liquid density in the absence of any external force except gravity. The equation includes the following functions: a speed of movement of liquid element v(x, y, z, t), density ρ(x, y, z, t) and pressure p(x, y, z, t) [2] . The internal friction (viscosity) and the heat exchange between the individual elements are ignored. This liquid is called perfect and is a space with constant entropy. The movement of each member of such a liquid occur with conserved entropy. In the absence of a sound wave, the average velocity of the liquid element is equal to zero. By definition, the pressure is a force that is acting on a unit area of a surface perpendicular the force. Force is a vector as is known. In liquid which is not subject to external influence, pressure between the individual elements of the liquid takes all possible directions. In averaging over him received the above-mentioned equation of motion. The velocity of the fluid element initially considered small. In [2] it is assumed that under the influence of a sound wave density and pressure vary on the value of ρ′ and p′, which is much less than the equilibrium values of ρ0 and p0. It is assumed that all three functions v(x, y, z, t), ρ′(x, y, z, t) and p′(x, y, z, t) perform synchronous oscillations of small amplitude with frequency of the sound wave. As a result, for the quantities v, ρ′ and p′ the following equations received [2] :
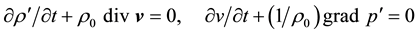 (1)
(1)
Equations (1) is not enough to determine the three quantities v, ρ′ and p′. It is assumed that ρ′ and p′ are proportional to each other, and the proportionality factor is the speed of sound c: ρ′ = p′/s2. As a result, the first equation from (1) takes the form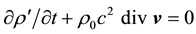 . Thus, the equations obtain for the v and p′ in a space where operates the sound wave. The usual way of solving differential equations (finding and v and p′) consist in adding to the right sides of (1) the acting force (sound waves) and the initial conditions [4] . That the initial conditions are absolutely necessary, it is clear from the second Equation (1): it is the velocity vector of the sound is determined by the gradient of the scalar quantity p′. This means that the speed will be the direction at which gradient is taken, [4] , i.e. it must be given in initial conditions. Instead of it in [2] introduced a scalar potential function, which is expressed by both unknown quantities v and p′. Both Equation (1) are reduced to a single second-order equation called the wave equation, (WE), the solution of which is the potential function. Solutions WE will be discussed below.
. Thus, the equations obtain for the v and p′ in a space where operates the sound wave. The usual way of solving differential equations (finding and v and p′) consist in adding to the right sides of (1) the acting force (sound waves) and the initial conditions [4] . That the initial conditions are absolutely necessary, it is clear from the second Equation (1): it is the velocity vector of the sound is determined by the gradient of the scalar quantity p′. This means that the speed will be the direction at which gradient is taken, [4] , i.e. it must be given in initial conditions. Instead of it in [2] introduced a scalar potential function, which is expressed by both unknown quantities v and p′. Both Equation (1) are reduced to a single second-order equation called the wave equation, (WE), the solution of which is the potential function. Solutions WE will be discussed below.
The main objection to the above-described interaction of sound waves and the liquid is as follows. To activate the vibrator motion of the individual elements of the fluid throughout the propagation path of the sound wave requires a considerable expense of energy. It is not in agreement with the experimental data. [5] presents the results of calculating the energy of the light wave required to excite vibrations in her transparent to light environment. It was found that this energy is only enough to excite vibration motion of a single electron revolving in its orbit around the atom. On the oscillatory motion of heavier particles the energy of the light wave is not enough. It is hard to imagine that the propagation of sound waves at thousands of kilometers the energy will be enough to excite mechanical vibrations of all the particles in the fluid pathway.
A number of authors, for example, [6] [7] , it is proposed to describe the propagation of sound waves by means of deformation of liquid under the force (pressure) mechanical vibrations caused by the timing vibrations of the membrane, creating a sound wave. About the process of deformation it is known that it is the contraction of the liquid which transmits the pressure of the sound wave adjacent layer. From experiments it is known that the sound wave is transmitted through the liquid space and reached the hydrophone saves time dependence of the signal and its relative value. In the process of propagation of a sound wave interaction with the environment is such that do not alter noticeable way the original spatial-temporal structure of the sound wave.
It is known that the aqueous medium has a very low compressibility, numerically consider it quite difficult. In liquids, [8] , the distance between the molecules of the order of molecular dimensions, i.e. ≈ 10−10 m. The intermolecular interaction is electrical in nature, and is the sum of the forces of attraction (orientation, induction and dispersion) and repulsive forces. It is believed that water molecules compression (compaction) takes place within the spatial size of the potential hole of the energy function of the Lennard-Jones (A-D). Branch (left) of the potential hole A-D, “responsible” for the repulsion of molecules as they approach the position of the minimum in the potential hole has a larger (at times) the gradient than the right branch which is “responsible” for their attraction. This gives rise to a large “elastic force”, i.e. it works like Hooke’s law for small strains. Distance limit convergence centers for water H2O molecules about 4 × 10−26 m. Pulled together the atoms of the molecules [9] overlap with their electron shells generating systems (electronic terms). The energy levels of the system are functions of the distance between the nuclei giving rise to repulsive forces. In our opinion, the intermolecular interaction is one of the basic mechanisms of transmission of the pressure wave. At the same time self-interaction of water molecules themselves is strong enough [10] . They can be combined with each other through the exchange of hydrogen atoms, forming the peculiar clusters of various configurations. These structures also interact with each other, forming already disordered, but big enough elements (clusters) of liquid. To make clusters oscillate with the frequency of a sound wave, or disrupt the structure of clusters, breaking them down into individual molecules, the energy of the sound wave may not be enough.
On the basis of these well-known facts about the equilibrium structure of a liquid which is not subject to external influence, we can draw the following conclusion. The pressure of the sound wave makes deformation of the liquid layer, which it reached. Deformation of the liquid occurs strictly in a plane perpendicular to the direction of the vector pressure. It is assumed that this initial compression (pressure) is passed from one layer to another at the expense of power (energy) of the intermolecular repulsion in the direction of wave propagation. That form of a sound wave is not distorted it indicates the following. The transfer of pressure from one layer to another, and return the liquid to the unperturbed state occur in a time much less than the oscillation period of the sound wave. Passage to the original liquid unperturbed state is explained by the law of conservation of entropy in the liquid. This means that for any external influences after their end there is come pre-existing state of the liquid. Therefore, the transfer of deformation to adjacent layer is set in the previous undisturbed state, will not experience any changes during the passage of the sound wave. When the period of the sound vibrations less the time to return the liquid to its original state of equilibrium, then the absorption of sound waves comes and the distortion of its shape. Therefore, at that moment it is impossible to write the equation of sound propagation in the medium, just as Maxwell’s equations were obtained. But for the propagation of the sound waves is enough to know its velocity, experimental measured, as well as for the propagation of EM waves in vacuum.
3. The Paradox of the Name “Running Wave”. The Role of Wave Equation in Acoustics
Running waves in acoustics described by the following function:
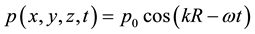 (2)
(2)
where p0―the amplitude of the wave, scalar, R―vector defining the trajectory of the wave, k―wave vector, its direction coincides with the direction of R. It is believed that the expression (2) is universal and fully describes the propagation of waves. This means that (2) is applicable to any type of audio sources and any direction of wave propagation, since no restriction of applicability speak. It is known that the phase of the periodic type functions cosϕ, sinϕ always―the scalar. Indeed, in determining (2) the direction of propagation of the sound wave is absent, although the phase consists of two vectors, but the scalar product of parallel vectors kR, ―scalar. In [11] it is shown that the direction of the waves should set the initial conditions as is done in the solution of any problem. The sound wave is a vector perpendicular to the plane of the vibrating membrane. We propose to introduce the direction of propagation of the wave in it amplitude, consider it is a vector, which coincides with the velocity vector (trajectory) of sound in the liquid. It will reflect the physical essence of traveling wave―its propagation, and clearly mark its direction. Vector representation of the amplitude of the wave will eliminate unjustified change in the wave phase the value of π, produced by many authors to account the change in the sign of the reflected wave. When the amplitude is the scalar the sign of amplitude p(x, y, z, t) in (2) does not change during propagation. In addition to the need for a definition of semantic amplitude―vector of the running wave this results in line with its name. This notation is universal, applicable in any type of wave source, and any direction of wave propagation, because the phase ϕ of periodic functions of the type cosϕ, sinϕ is always a scalar quantity and not depend on the vector’s direction that forms it.
Consider the propagation of sound waves in their new form that we proposed. We assume that the source of the sound (temporary) fluctuations is a membrane placed in a liquid and performs mechanical oscillations of a given frequency ω:
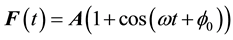 (3)
(3)
Here, A―the vector’s amplitude of the mechanical vibrations of the membrane, normal to the plane of the membrane, ω―frequency of oscillations, ϕ0―initial phase’s oscillations. With respect to the liquid the function F(t) is a mechanical force generated by the membrane, a vector directed perpendicular to the plane of the membrane in the direction of propagation of the sound wave. Let the force F(t) actions per unit area and is a pressure produced with membrane in liquid. In the expression (3) is present constant component. It reflects the fact that the wave propagates only in one direction, perpendicular to the plane of the membrane, a reverse movement in the direction to the source does not exist. It is this process of propagation corresponds to the above-described deformation of the medium, transmitting the action of a sound wave in one direction only. The pressure propagates in the liquid at a rate determined by the composition of the liquid. Since the speed of propagation of a mechanical pulse (oscillation) is finite, the point in space pressure of the sound waves (3) arrives at the instant t1, is equal to the running distance divided by the velocity of propagation of sound vibrations. Given t1, the delay time, write down the pressure on the liquid in the form of a running wave:
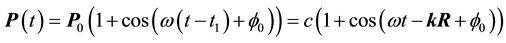 (4)
(4)
Here t1―time delay, during which passed the distance R. Vector wave amplitude coincides with the vector R in direction and proportional to the speed of sound. Therefore, in Equation (4) P0 is replaced by a vector with the speed of sound. At the present level of knowledge about the deformation of the liquid to describe the propagation of sound waves we use the expression (4).
It is possible that as a result of the search the direction in its phase, there are new types of waves that have no physical meaning. These are the solutions of the wave equation in wave propagation problems. Let us examine them in detail. We know that running sound (and EM waves) describes by differential equations of the first order. This Maxwell’s equations for electromagnetic waves and the equation of sound propagation in the fluid (1) obtained from the Euler equation and continuity of fluid density [2] [3] . As a rule, the majority of authors through a series of mathematical operations and assumptions replace the differential equations of the 1st order for sound and EM waves to a single equation of the 2nd order wave Equation (WE). This is done by introducing a special potential functions, through which, after finding them in solving WE determined strength of the EM field and the field of longitudinal sound wave. It should be noted that each component of EM fields and sound satisfy the WE and without the introduction of potential functions.
Solution of the wave Equation (the potential function f) consists of two functions:
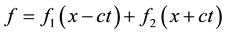
If we multiply the arguments of each function in the wave number k = ω/c, we find that they coincide with the phase of the running plane wave: . It is assumed that the first of them is running plane waves in the positive direction of the axis x, the second―in the opposite, negative direction.
. It is assumed that the first of them is running plane waves in the positive direction of the axis x, the second―in the opposite, negative direction.
In [11] it is shown that one of the solutions (second) WE for a sound wave, which argument (phase) of the running wave is the sum of spatial and temporal components, does not satisfy the differential equations of the 1st order, (1) obtained in [2] . We consider this decision WE in detail. Usually, the transition to the WE is considered as a plane wave along the x-coordinate. Its phase ψ′ = (kx + ωt) is treated as wave propagation in the opposite direction with respect to the x-axis, i.e. speed (c) in ψ′ changes sign(−c). This is misinterpretation of phase. It is known that the direction vectors of the trajectory and velocity of any moving object including a sound wave coincide, i.e. have the same sign. Therefore, you need to change both the signs and x and c. It will lead to the first decision having the difference of spatial and temporal components of phase.
Consider another solution WE (first) phase of the wave which is the difference between spatial and temporal components. All works published after the transition phase to a plane wave the phase has the form 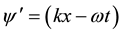 . With such record it is not clear what indicates x: either the length of the vector (its modulus), or the vector itself, or the final coordinate of the trajectory on the axis x. Proper recording phase for plane running waves:
. With such record it is not clear what indicates x: either the length of the vector (its modulus), or the vector itself, or the final coordinate of the trajectory on the axis x. Proper recording phase for plane running waves: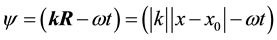 , and
, and 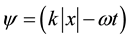 if |x0| = 0. The conclusion: the transition to a plane wave with no errors, the second solution is incompetent.
if |x0| = 0. The conclusion: the transition to a plane wave with no errors, the second solution is incompetent.
Returning to the solutions of WE. The source of the occurrence of an erroneous decision [2] in the transition to WE, is the introduction of new coordinates ξ, η instead of the existing x, t:
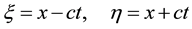
The physical meaning of the coordinate ξ is understandable, it is the phase of the running wave when both components are changing phase of the wave at the same time. The magnitude of the phase remains constant: to be zero or the initial phase of a running sound wave. Persistence of phase of any running wave―its basic property, it is choose of consideration, reflecting its dependence on the spatial and temporal coordinates. What consideration to choose―it depends on the particular formulation of the problem. The physical meaning of the coordinate η is not clear. Why is this phase of the “running” wave increases, what means that growth, what a physical process it describes. Obviously, the authors introduce these coordinates forget that x is always equal to the value of ct and both x and c have the same sign always. The fact that such function with such phase is a solution of WE, does not means that it actually exists. It should be noted that the replacement of the equations of motion adopted in [2] for the wave equation, does not alleviate the problem of spreading. Running sound wave satisfies both the Euler equation and the wave equation. As a result, it can be concluded that the replacement of the equations of liquid motion on the wave equation has no advantages, but adds additional solution that is not a running wave.
4. Vector Calculation of the Amplitudes of the Reflected and Transmitted Waves Traveling
The calculation of the amplitudes (coefficients) of the reflected (CR) and the passed (CP) of the sound waves at the interface of two homogeneous media with different propagation’s speeds is performed under certain conditions at the border. Traditionally, the boundary conditions consist in the fact that the sound wave excites vibrations of the pressure and velocity of the liquid particles with the wave frequency. The pressure is considered a scalar quantity, particle velocities―vectors [2] [3] . The boundary condition is follows: the sum of pressures of two waves on one side of the border (forward and backward) is equal to pressure passed sound wave on the other side of the border with the other speed of propagation of sound waves [2] [3] .
In [11] [12] indicated that in such a pressure boundary condition the incident wave is counted twice, i.e., it violated the law of conservation of energy. Indeed, above the boundary the pressure of incident wave is added to the pressure of the reflected wave, which has part of incident energy contribution. The resulting amount is equi- valent to pressure transmitted wave, which is the same as the reflection, arose from the incident, and its energy is already considered in the pressure of the incident wave above the media.
In paper [12] instead of the conditions for the pressures on the border of media use the law of conservation of energy: the energy of the incident wave is equal to the amount of energy transmitted and reflected waves. The results obtained in [12] CR and CP―cannot be considered completely reliable, because for some values of the refractive index of the value will be negative, what should not be.
We offer a new method of calculating the CR and CP. The basis of it is the idea of wave propagation as a process of deformation of the liquid in medium with the conservation of entropy. According to the experiment, the time dependence of the pressure of membrane on the liquid and the direction vector of pressure in homogeneous space remain constant. Let us assume that in the second medium emerged refracted wave propagates, as in the first without being absorbed. The appearance of new waves at the border environments does not violate the laws of conservation of energy and momentum. Therefore, at the boundary between two media should be considered as the conservation of the sound wave energy and conservation of momentum (vibration velocity) of the membrane. This means that the sum of vectors (pressure) of the reflected and transmitted waves must be equal to the vector of the incident wave, and the energy of the incident wave is equal to the sum of the wave’s energies occurring at the boundary areas. Theirs directions determine by Snell’s law. In [11] carried out the vector addition of the waves, but the desired result is not given, because instead of the law of conservation of energy waves it is traditionally consider: the summer CR + CP = 1. Such conservation’s law does not exist. In [12] the energy conservation law is applied correctly, but the vector addition of the waves was only used for the vertical component of the waves, the horizontal components of the waves are not taken into account.
In this paper, each wave is regarded as a vector having its direction and its size (length). The energy source of the incident sound wave is proportional to the square of the speed of oscillation of the membrane. The direction of the pressure created by it coincides with the vector perpendicular to the plane of oscillation of the membrane and determine by initial conditions. This direction is the direction of propagation of the wave in the liquid. The magnitude of the velocity of propagation is determined by the environment and is the only known characteristic of the medium, which determines the propagation of sound waves in the liquid. Hence we identify the vector pressure generated by the sound wave, with the direction of oscillation of the membrane, and the pressure at a speed of sound in the liquid. There is no reason to select, as a particular characteristic of the medium, its density, despite the fact that it is easy to measure. The density ρ of the environment as one of the parameters, of course, affect the value of the speed of sound. At this point, to account for the density of the medium ρ during the deformation of it by sound wave, no equation in which it was part, such as in Equation (1) used to describe the propagation of sound in [2] [3] .
In papers [11] [12] is showed that all three phases of waves no part in calculating the coefficients CR and CP do not accept. Recall that the initial phase of wave occurred at the interface is the phase of the incident wave. From it be gins the phase of the reflected and passed waves, phase jump absent, coherent wave persists. The growth phase of each wave occurred is determined by its path and environment settings. Knowledge of the phases need only to calculate the value of the sound field along the trajectory to compare it with the other ray’s field, come to this point, if we consider the interference of waves.
Let the wave incident on the interface of the medium with the velocity of sound c above the boundary, and lower it at a rate of c1. The ratio of their modules (refractive index) n = c/c1 can be either smaller or greater than 1. Let us assume that the plane of incidence is the plane (x, z). We introduce the following notation: index i, R, t, propagation angles θ, θ′, θ1 and the unit vectors ni, nR, nt refer respectively to the incident, reflected and transmitted waves. Vector amplitude of the incident wave is nic, reflected―nRcV, passed―ntc1W. Modulus of the amplitude of the incident wave |c|, reflected and transmitted waves |c|V and |c1|W-positive values. Let the direction of each wave entering the unit vectors. Then the pressure of sound waves (2) vector can be written:
 (5)
(5)
Figure 1 shows the arrangement of all three waves (rays) at both sides of the border. Showing angles θ, θ′, θ1 and the direction of the unit vector along the trajectories of the waves.
Consider the conditions for the emergence of new wave at the border. Assume that all three waves pass the
Figure 1. Arrangement rays near the interface.
same distance. R = Ri = Rr = Rt. Distances Ri., Rr waves passed for one and the same time t0 = R/c, since their speeds of propagation equal. During the same time t0 waves shifted along the x-axis at the same distance , xb, zb―coordinates of the point on the border, from where the incident wave is formed reflected and refracted waves. Since horizontal displacements are projections Ri, Rr at axe x, then their projections are equal to each other, Risinθ = Rrsinθ′. It follows that the angles of the incident and reflected waves with respect to the z axis coincide, θ = θ′. Propagation time transmitted beam in the second medium t1 = Rt/c1 on the same distance R less t0. Propagation of sound in the second medium is faster than in the first. At the boundary the continuity of layer of liquid perpendicular to the axis x, may be breach. That layer transmits sound wave by deformation of the medium. To avoid this, you must accept that the same propagation times of the projections of the vectors Rr and Rt on the axis x: (Rr/c) sinθ = (Rt/c1) sinθ1. Given that Rr = Rt we obtain the relation of angles of incidence and refraction and the speed of sound on both sides of the border: sinθ/c = sinθ1/c1. It is a well- known Snell’s law. It is fully consistent with the proposed mechanism of deformation of the medium in the propagation of the sound wave. It means that liquid layers on both sides of the border are deformed in a way that their propagation times along axis x, at boundaries coincide, ‘slip’ of the liquid particles to each other does not occur.
, xb, zb―coordinates of the point on the border, from where the incident wave is formed reflected and refracted waves. Since horizontal displacements are projections Ri, Rr at axe x, then their projections are equal to each other, Risinθ = Rrsinθ′. It follows that the angles of the incident and reflected waves with respect to the z axis coincide, θ = θ′. Propagation time transmitted beam in the second medium t1 = Rt/c1 on the same distance R less t0. Propagation of sound in the second medium is faster than in the first. At the boundary the continuity of layer of liquid perpendicular to the axis x, may be breach. That layer transmits sound wave by deformation of the medium. To avoid this, you must accept that the same propagation times of the projections of the vectors Rr and Rt on the axis x: (Rr/c) sinθ = (Rt/c1) sinθ1. Given that Rr = Rt we obtain the relation of angles of incidence and refraction and the speed of sound on both sides of the border: sinθ/c = sinθ1/c1. It is a well- known Snell’s law. It is fully consistent with the proposed mechanism of deformation of the medium in the propagation of the sound wave. It means that liquid layers on both sides of the border are deformed in a way that their propagation times along axis x, at boundaries coincide, ‘slip’ of the liquid particles to each other does not occur.
The calculation of the amplitudes of the reflected and transmitted waves is made on the rule of vector addition of pressures (5) at the interface after eliminating (reducing) of the same phase factor:
 (5′)
(5′)
This is the law of conservation of momentum. We write the projections of the amplitudes on the coordinate axes (x, z), according to the rule of vector addition [13] :
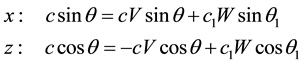 (6)
(6)
Signs projection component of all three waves in (6) are defined by their direction of propagation with respect to the axes (x, z) of Figure 1. Note that the second of the Equation (6) is used in all methods of calculating CR and CP. The next step―to divide each equation at c1 and to put in square their left and right sides. After that, the two equations are added:

This equation expresses the law of conservation of amount of movement (momentum). The law of conservation of energy does not depend on the direction of wave propagation and has the form:
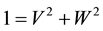
As a result of the laws of conservation of momentum and energy we obtain the following expression for the amplitude V and W:

Consider the characteristics of amplitude V and W (8). First, we note that the formula (8) are applicable for any of the coefficient of refraction n, greater than or less than 1. This is easily seen, replacing n2 in terms of V2
and W2 with 1/n2. Expression 
waves V, W―always positive values, so if n > 1 we must take 

Such a bond angle of the incident and the refractive index is observed in the optical [13] when on the basis of the Fresnel formulas for the CR and CP considered EM energy (light) wave incident on a unit area of the interface between two media. When the condition θ + θ1 = π/2, the electric vector of the reflected wave does not have a component in the plane of incidence. This angle is called Brewster angle, or angle of complete polarization: reflected and refracted rays are perpendicular to each other, as well as for sound waves. Formulas for the CR and CP sound waves almost coincide with the formulas for CR and CP EM waves (Fresnel formulas). Upon receipt of the formulas for EM waves summation of wave’s projections on the coordinate axes is carried. On the contrary, in the preparation of the formula (8) in addition to a similar process of vector addition using the laws of conservation of momentum and energy instead of an erroneous condition of equality pressure on both sides of the border, is traditionally used for audio and for EM waves.
The traditional formula for the CR and CP [3] when θ1 = π/2 and sinθ1 = 1, is considered to be an angle of FIR, angle θcr = arcsin(n), called critical. When θ = θcr according to the formulas for the CR and CP, [3] , V = 1 and W = 0. Along the border of the transmitted wave does not exist because V = 1. Therefore, the angle θcr named in [3] the angle of FIR, a wave reflected from the boundary and returns to the starting medium. Based on this in [11] [12] proposed to assume that in oceanic waveguides turn of trajectory does not occur at 90˚, where sinθ = sinθcr = n. As follows from the expressions (8) to V and W, when θ1 = π/2, 
Consider the numerical calculation of the amplitudes of the reflected and transmitted waves by (8). Figure 2 shows the amplitude V and W of the angle of output (falling) θ in the range of angles from zero to angle defense inclusive. V curves of black, W red refractive indices: n1 = 0.766 (the lower curve of W and the uppermost V), n2 = 0.866, n3 = 0.940, n4 = 0.985 (W―most riding the curve at the top and V―the lowest below). For these values of n using the formulas for the CR and CP, [12] , obtained the following values of the output angle θ = θ1 ? θ4, which takes place FIR: 50˚, 60˚, 70˚ and 80˚, i.e., their position on the axis of the output angle proportional to the angle output. As can be seen from Figure 2 at small angles of output amplitude of the transmitted waves W are close to 1 for all values of the coefficient n, the amplitude of the reflected wave V does not exceed 0.3. Area FIR angles of the incident wave at all values of n lies in a small range of angles output θ, between 37˚ and 45˚. When n = n1 FIR angle occurs when the output of the reflected beam angle θ = 37.457˚ and last θ1 = π/2 − θ = 52.52˚. When n = n4 FIR occurs when the output angle θ = 45.44˚, passing angle θ˚ = π/2 − θ = θ1 = 44.56˚.
Figure 3 shows the dependence of V and W of θ for the same values of the refractive indices, as in Figure 2, but in the whole range of angles of exit beams from the source. Designations in Figure 3 are the same as in Figure 2. The length of each curve at high angles of the output is limited to the value of the refractive index, sinθmax = nsinθ1 < 1 may not exceed 1.
Figure 4 shows the dependence of V(θ), W(θ) for n > 1. For each number of the curve in Figure 4 value n equal to the reciprocal value n to the curve of the same numbers in Figure 3. It is made with a view to analyze the relationship between the curves in Figure 3 and Figure 4. It can be seen that for n > 1 field angles defense in
Figure 2. V, W -amplitude of the reflected and transmitted sound waves at n < 1. Curve 1. n = 0.7666; 2. n = 0.8666; 3. n = 0.94; 4. n = 0.985.
Figure 3. V, W-amplitude of the reflected and transmitted sound waves at n < 1. Curve 1. n = 0.7666; 2. n = 0.8666; 3. n = 0.94; 4. n = 0.985.
Figure 4. V, W-amplitude of the reflected and transmitted sound waves at n > 1. Curve 1. n = 1.304; 2. n = 1.154; 3. n = 1.064; 4. n = 1.015.
Figure 3 and Figure 4 do not coincide. Angles defense shifted in Figure 4 in the range of values θ > 45˚, while the angular width of the area FIR remains the same.
5. Conclusions
It is proposed to consider the process of propagation of sound in adiabatic liquid as deformation of the liquid under the influence of a sound wave without appreciable interaction with the environment. This propagation of sound waves is similar to propagation of electromagnetic waves in a vacuum. It is not needed in writing the equations of motion for the sound waves in the medium, since detailed interaction of waves with the environment and their mutual influence on each other are not known currently.
It is proposed not to use the wave equation to describe the propagation of sound waves in a fluid. The currently used to determine the equation of motion of the sound wave propagation in the fluid give the same solution in the form of a traveling sound wave and that wave equation. The second solution of the wave equation, in which the phase of the wave is constantly growing, does not satisfy the equations of motion, has no physical meaning, and should be discarded.
It is received the formulas for the amplitudes of the reflected and transmitted sound waves at the boundary of homogeneous liquid medium on the basis of the law of conservation of momentum (pressure) wave, the law of conservation of energy and Snell’s law. The formulas for calculating the amplitudes of the waves do not depend on the phases of the waves, as in all previous calculations of the coefficients of reflection and transmission of waves.
It was found that there is a phenomenon of total internal reflection in the liquid refractive index n at both smaller and larger than unity. The calculation showed that the combined n ranging from 1.3 to 0.7, the range of angles output from the source, for total internal reflection is ≈7 - 8 degrees. By increasing the exit angle from the source, its region is shifted in the direction of increasing angles.
Cite this paper
V. P.Ivanov,G. K.Ivanova, (2015) To the Question of Sound Waves Propagation in Liquid. Open Journal of Acoustics,05,112-121. doi: 10.4236/oja.2015.53010
References
- 1. Gorelik, G.S. (1959) Oscillations and Waves. 2nd Edition, FM Press, Moscow.
- 2. Landau, L.D. and Lifshitz, V.M. (1988) Hydrodynamics. Science Press, Moscow.
- 3. Brekhovskikh, L.M. (1973) Waves in Layered Media. Science Press, Moscow.
- 4. Smirnov, V.I. (1958) A Higher Mathematics Course. Vol. 2, Moscow.
- 5. Landsberg, G.S. (1940) An Optics, Moscow.
- 6. Haykin, S.E. (1947) A Mechanics, Moscow.
- 7. Shabalin, O.D. (1981) A Mechanics and Acoustics Physical Principles, Moscow.
- 8. Kaplan, I.G. (1982) Introduction to the Theory of Intermolecular Interactions. Nauka Press, Moscow.
- 9. Landau, L.D. and Lifshitz, V.M. (1963) Quantum Mechanics: Non-Relativistic Theory. Moscow.
- 10. Bernal, Dg.D. (1967) Structure of liquids, Quantum macrophysics. Vol. 5, Science Press, Moscow.
- 11. Ivanov, V.P. and Ivanova, G.K. (2013) Some Aspects of Ray Representation Running Sound Waves in Liquid Spaces, Open Journal of Acoustics, 3, 7-13.
http://dx.doi.org/10.4236/oja.2013.31002 - 12. Ivanov, V.P. and Ivanova, G.K. (1913) A New Concept of Calculation Coefficients of Reflection and Passage Sound Waves on the Boundary of Liquid Spaces. Open Journal of Acoustics, 3, 72-79.
http://dx.doi.org/10.4236/oja.2013.33012 - 13. Born, M.A. and Wolf, E. (1965) A Principles of Optics. Pergamon Press, New York.





