Open Journal of Acoustics
Vol.04 No.04(2014), Article ID:52597,9 pages
10.4236/oja.2014.44020
Optimizing the PMCC Algorithm for Infrasound and Seismic Nuclear Treaty Monitoring
Anthony M. Runco Jr.1, James A. Louthain2, Dean A. Clauter3
1Space and Missile Systems Center, United States Air Force, Los Angeles Air Force Base, El Segundo, CA, USA
2Leidos Inc., Beavercreek, OH, USA
3Air Force Technical Applications Center, United States Air Force, Patrick Air Force Base, Cocoa Beach, FL, USA
Email: anthony.runco@aya.yale.edu, james.louthain@gmail.com, dean.clauter@us.af.mil
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 October 2014; revised 15 November 2014; accepted 16 December 2014
ABSTRACT
We introduce novel methods to determine optimum detection thresholds for the Progressive Multi-Channel Correlation (PMCC) algorithm used by the International Data Centre (IDC) to perform infrasound and seismic station-level nuclear-event detection. Receiver Operating Characteristic (ROC) curve analysis is used with real ground truth data to determine the trade-off between the probability of detection 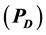 and the false alarm rate (FAR) at various detection thresholds. Further, statistical detection theory via maximum a posteriori and Bayes cost approaches is used to determine station-level optimum “family” size thresholds before detections should be considered for network-level processing. These threshold-determining methods are extensible for family-cha- racterizing statistics other than “size,” such as a family’s collective F-statistic or signal-to-noise ratio (SNR). Therefore, the reliability of analysts’ decisions as to whether families should be preserved for network-level processing can only benefit from access to multiple, independent, optimum decision thresholds based upon size, F-statistic, SNR, etc.
and the false alarm rate (FAR) at various detection thresholds. Further, statistical detection theory via maximum a posteriori and Bayes cost approaches is used to determine station-level optimum “family” size thresholds before detections should be considered for network-level processing. These threshold-determining methods are extensible for family-cha- racterizing statistics other than “size,” such as a family’s collective F-statistic or signal-to-noise ratio (SNR). Therefore, the reliability of analysts’ decisions as to whether families should be preserved for network-level processing can only benefit from access to multiple, independent, optimum decision thresholds based upon size, F-statistic, SNR, etc.
Keywords:
Progressive Multi-Channel Correlation, PMCC, Infrasound, Nuclear Treaty Monitoring, Detection Optimization

1. Introduction
The Progressive Multi-Channel Correlation (PMCC) algorithm is the underground and atmospheric detection method of choice for the international monitoring community that seeks to ensure compliance with the Comprehensive Nuclear-Test-Ban Treaty (CTBT). The community, or more specifically the International Monitoring System (IMS), leverages four global sensor networks―the radionuclide network, the hydroacoustic network, the seismic network, and the infrasound network. The seismic and infrasound networks chiefly employ PMCC to detect nuclear testing being conducted underground and in the atmosphere respectively.
The detection screening process occurs in stages―first at the individual station level and then at the network-processing level. For instance, when infrasonic waves produced by an explosion traverse an infrasound array, PMCC data processing at that individual station array should declare a potential nuclear event. When other adjacent arrays also declare detections, it is the goal of network-level processing to triangulate the location of the nuclear testing site based upon the time difference of arrival of the explosion-produced waves at these identified stations. Improving the efficiency of the automated screening at the station level implies lowering the burden on analysts whose collective responsibility it is to nominate station-level detections for network-level processing.
In other words, the goal of station-level processing would ideally be to maintain a high fidelity of true positive detections while limiting the number of false alarms. Considering this goal, surprisingly little is known not only about the performance capability of PMCC, but also about how the choice of PMCC parameter settings affect this performance. This research therefore evaluates the parameter of utmost import to PMCC―the consistency― as well as presents a novel method to determine optimum detection thresholds using classical detection theory.
2. Background
Any organization with a vested interest in the understanding and performance improvement of PMCC, such as the IMS, the IMS’s data processing International Data Centre (IDC), or the Air Force Technical Applications Center (AFTAC), stands to benefit from the PMCC parameter evaluation and optimum threshold method herein described. Analysis of PMCC should rightly begin with an explanation of its algorithm, the subject of this section.
2.1. PMCC
As a correlation detector, PMCC begins by assuming that infrasound-producing events are far enough away from surrounding sensor arrays that the arrays can treat the propagating infrasound signals as plane waves. Plane wave propagation implies that the wave front will traverse an array’s horizontally displaced sensors in succession. The time delay in plane wave arrival at one sensor element relative to another can be calculated via cross- correlation of the two infrasound sensor elements’ measured atmospheric pressure variations. Cross correlations are performed within an analyzing time window of length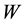 , where the channel data of sensor
, where the channel data of sensor 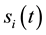 is shifted over the channel data of sensor
is shifted over the channel data of sensor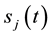 . Note that an infrasound signal in the time domain
. Note that an infrasound signal in the time domain 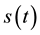 can be represented in the frequency domain by its Fourier transform
can be represented in the frequency domain by its Fourier transform
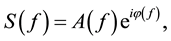 (1)
(1)
where 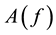 represents the spectral amplitude, and
represents the spectral amplitude, and 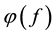 represents the spectral phase. Given plane wave presence, the time shift at which the cross correlation is a maximum,
represents the spectral phase. Given plane wave presence, the time shift at which the cross correlation is a maximum,
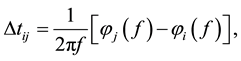 (2)
(2)
indicates the time difference of a signal’s arrival between the two sensors.
A plane wave produces a consistent set of time delays
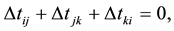 (3)
(3)
satisfying what is known as the closure relation. In the presence of background noise, the cross correlation operation may be less accurate due to random phase combinations, and the delays may not sum exactly to zero. The consistency of the set of time delays for 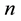 sensors of sub-array
sensors of sub-array 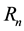 is defined as the mean quadratic residual of the closure relation, expressed as follows:
is defined as the mean quadratic residual of the closure relation, expressed as follows:
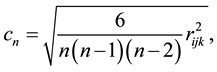 (4)
(4)
where 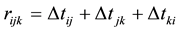 and
and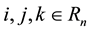 . If the calculated consistency is below an established threshold, i.e. tolerably close to zero, a detection is declared on
. If the calculated consistency is below an established threshold, i.e. tolerably close to zero, a detection is declared on  [1] .
[1] .
Once a detection is declared, the time delays producing that detection are known and are subsequently inverted to obtain estimates for the propagating infrasound signal’s velocity and azimuth [2] . To explain how inversion is possible, consider the following example: A plane wave propagating from a known, fixed location at a specific velocity allows one to predict exactly when the signal will arrive at each sensor element within an array―and therefore the time differences of arrival from sensor to sensor. Likewise, PMCC calculations yielding time differences of arrival from sensor to sensor permit the trace velocity and azimuth to be estimated.
PMCC begins by determining the consistency on a set of delays for the smallest triangular sub-array. The signal’s trace velocity and azimuth, as determined by inverting the closure relation’s time delays, are then used to “direct” the search for other sensors that may be added to the initial sub-array. Specifically, the value of the expected time delay for a pair of sensors, in which one of the sensors is outside the original consistency-eva- luated sub-network, can be estimated. The computed time delay for this sensor pair corresponds to the correlation local maximum that is closest to the given estimate. As long as the detection criterion continues to be valid, i.e. the consistency threshold is met, the aperture of the network increases with each added sensor. As a result, velocity and azimuth estimates become more and more refined [3] .
2.2. WinPMCC
Prior to running PMCC’s detection algorithm, a filter configuration filters the data in infrasound frequency passbands of interest. After canvassing an array’s sensor-recorded data for infrasound arrivals, a list of elementary detections satisfying the consistency threshold remains. These elementary detections are known as pixels within the WinPMCC program that implements the PMCC algorithm. An almost constant stream of pixels is created in time-frequency space. The seemingly innumerable elementary detection list exists in no small part due to the ambiguity involved in the progressive search for distant sensors to add to initial sub-arrays.
WinPMCC’s solution to this pitfall is to build pixel families, or group pixels that are similar in time-frequen- cy-velocity-azimuth space and can therefore be associated with the same infrasound arrival [4] . An example of a WinPMCC-produced family is illustrated in Figure 1. In addition to eliminating pixels that cannot be associated with neighboring pixels, PMCC families help distinguish multiple arrivals that may exist in the same time window but in different frequency bands. Two pixels, 


where 










3. Methodology
The ultimate question of station-level processing is what to do with its primary product, the list of potential detections or families. Which families were produced as the result of an infrasound event of interest? Stated another way, which families should be nominated for network-level processing? And is there a family-characte- rizing statistic that can help in discriminating true events from non-events? This research suggests family size is a viable candidate.
3.1. Ground Truth Set
A prerequisite of this analysis is the establishment of a ground truth (GT) set of true detections. Three independent programs assist in building the set. Specifically, detections determined by WinPMCC are compared and contrasted with detections determined by Dr. Arrowsmith’s InfraMonitor [6] , which is a modified F-statistic de-
Figure 1. WinPMCC-produced family resulting from an infrasound arrival on 25 August 2011 at 03:14:15 at the BRD array situated along the Korean Demilitarized Zone. The sensor data, as shown, have been filtered by a band pass butterworth filter with −3 dB cutoffs of 2.0 Hz and 4.0 Hz.
tector adapted to account for ambient noise. In other words, InfraMonitor is designed not to declare detections, nor one long detection, for infrasound produced by a repetitive/continuous source, such as microbarom ocean swells [6] . A third program, SeaTools, proves useful in resolving whether detections flagged by either one or the other of these two detectors (but not both) are, in fact, true detections. SeaTools is a waveform analysis program initially developed by AFTAC to review seismic data. These three programs are used in concert to ensure the GT set is not biased towards any one program. The data analyzed for this research was recorded during the month of August 2011 by five infrasound arrays in East Asia. Figure 2 provides more detail on exact station locations.
It should be clarified that a true detection, indicating what is considered to be an “event” as opposed to a “non-event,” may not actually signify a performed nuclear test and, in fact, is more likely to signify a chemical explosion produced as the result of mining operations, for instance. This reality does not affect the legitimacy of the method by which optimum detection thresholds are determined, however, since there is no discernible difference so far discovered between the infrasound produced by a nuclear explosion and the infrasound produced by a chemical explosion of an equivalent infrasound-producing explosive yield. Considering that approximately 50% of a nuclear explosion’s energy is converted into a blast wave as opposed to nearly all of a chemical explosion’s energy, a nuclear explosion’s infrasound-producing equivalent yield is approximately twice that of a chemical explosion’s [7] . In the absence of a nuclear signature or “fingerprint,” the best station-level processing can do is to reduce the rate of false alarms that are the result of noise, continuous/repetitive sources such as ocean swell microbaroms, mountain associated waves, etc., while also avoiding missing infrasound events of interest, such as explosions. The goal of optimality, therefore, is to ease the burden on analysts whose responsibility it is to reduce station-level detections to a narrower list for subsequent network-level processing. It is then the job of network-level processing to confirm or deny station-level-nominated nuclear testing candidate events.
3.2. Consistency Threshold
With a completed GT set, WinPMCC detector performance is now judged based upon how varying the consistency threshold affects the trade-off between the probability of detection 
Figure 2. The GT set is constructed from signal of interest (SOI) arrivals on the three arrays located along the Korean Demilitarized Zone (BRD, CHN, KSG), one array located in Japan (I30), and one array located in Russia (I45).
PMCC producing a family is its way of declaring a detection. That declaration is either a true detection or a false alarm, and a receiver operating characteristic (ROC) curve is built based upon the accuracy of these declarations at various consistency thresholds.
WinPMCC families produced as a result of the use of a given consistency threshold that correctly identify a detection included in the GT set are counted among true positive detections, while those that cannot be associated with GT set detections are categorized as false alarms. The equation governing true detections is, intuitively,

Alternatively, the probability of false alarm would be calculated as

However, this probability relies on the ability to assign a finite value to the denominator, the total number of negative detections. Considering that WinPMCC analyzes a time window of data within which the absence of detections cannot be quantified, false alarm occurrence is expressed on a per day rate basis, calculated as

and, as a result, the ROC curve characterizing the 
3.3. Optimum Family Size
From the perspective of an analyst reviewing the list of families produced by WinPMCC, a decision has not yet been made as to whether a signal of interest (SOI) is present or not. Though Equation (6) and Equation (8) provide insight into WinPMCC’s expected performance at various consistency threshold settings, the analysis needs to be taken a step further to assist analysts in determining which station-level families should be nominated for network-level processing. “Preserve only the largest and most stable families” is about the extent of the guidance analysts are given [8] . However, no clarification is proffered as to what constitutes a “large” or “stable” family.
The optimum family size is determined with a maximum a posteriori (MAP) approach in which the goal is to minimize the total number of false alarm and missed detection categorization decisions. Specifically, the solution to this approach indicates how many pixels must comprise a family before it is more likely than not that the family represents a true infrasound SOI arrival.
The first step in this approach requires organizing the GT set according to the number of pixels comprising each detection. The frequency with which a particular family size appears as a detection is then recorded. This process is repeated until every detection in the GT set is accounted for, and a probability histogram is created to visualize the distribution of family sizes. The histogram is then curve-fit with the probability density function (pdf) that best characterizes its distribution, as in Figure 3. This pdf is known henceforth as the conditional distribution of family sizes given the detection is a true event family, or



Figure 3. Probability histogram of GT set family sizes. Overlaid onto the histogram is the Lognormal pdf, 
Figure 4. Probability Histogram of non-event family sizes. Overlaid onto the histogram is the exponential pdf, 
The decision criteria are arranged in a likelihood ratio test (LRT)

which forms an inequality between the ratio of the true detection and rejection conditional probability density functions and the ratio of the a priori probabilities of the presence 







Returning to the optimality discussion, the terms of Equation (9) are now rearranged to position the true event and non-event likelihood functions on either side of the inequality, as follows:

The true event likelihood function, 





4. Results
The Methodology section explored the consistency threshold insofar as it presents a trade-off between the probability of detection and the false alarm rate. The choice of how to set this threshold within the WinPMCC program has a direct impact on WinPMCC’s performance prior to any higher level human assessment. Additionally, a method was developed by which to determine optimum detection thresholds to assist precisely with the analysts’ higher-level assessments as to whether or not a SOI is actually present.
4.1. Consistency Threshold and the Receiver Operating Characteristic
The consistency-dependent trade-off between 




4.2. Optimum Family Size Detection Thresholds
When determining optimum family size detection thresholds, the consistency threshold was set at 0.1 sec.
4.2.1. Maximum a Posteriori Threshold
Recall from Figure 3 that the lognormal distribution best fit the true event probability histogram. And, as may intuitively be expected, the exponential distribution in Figure 4 captures the higher likelihood of smaller family sizes in the case of SOI absence. At least two pixels must be grouped together before constituting a family.
Ultimately, the intersection of the likelihood functions is depicted in Figure 6. The MAP threshold for this examined data is 12 pixels per family, i.e.








Figure 5. Pseudo-ROC curve presenting the trade-off between the probability of detection 



Figure 6. The maximum a posteriori threshold 




tection, missed detection, false alarm, and rejection respectively.
4.2.2. Bayes Decision Criteria and Risk Minimization
If instead of minimizing the probability of categorization error, the goal is to minimize the cost-based risk associated with those categorization decisions, Bayes decision theory supplants the MAP approach. At the prerogative of a monitoring agency, such as the IDC, costs can be assigned to each of the following four potential events: detection, rejection, false alarm, and missed detection. Although the value for these costs is somewhat arbitrary, typically 


The terms of Equation (11) are now rearranged so as to position the Bayes-scaled likelihood functions on either side of the inequality in the following manner [10] :

The true event and non-event family size likelihood functions are scaled by the previously assigned costs. As was the case for the MAP threshold, the optimum Bayes threshold is marked by the graphical intersection of the functions on either side of Equation (12)’s inequality.
Using 100, 20, 10, and 0 for the costs of a missed detection, false alarm, true detection, and rejection respectively, the resulting Bayes threshold 



The Bayes approach seeks to minimize the expected value of the decision outcome costs. Since the highest cost was assigned to a missed detection, the least likely outcome for Bayes threshold-based decisions is indeed a missed detection. Decisions based upon such a threshold imply the following decision outcomes:



5. Conclusion
Consider the impact of these results, WinPMCC consistency settings have been tied to expected detection performance. The optimum threshold determination procedures detailed above can be applied to individual stations at the discretion of the IDC, thereby producing station-specific optimum thresholds. The IDC does not currently use any family-characterizing statistic as a detection threshold, but this research’s results suggest that family size is a viable candidate. Moreover, family size is not the only viable family-discriminating candidate. The optimum threshold determination method is extensible to other family characteristics as well, such as a family’s collective F-statistic or signal-to-noise (SNR) ratio. Each of these characteristics can be used to create optimum thresholds. The reliability of analysts’ decisions as to whether families should be preserved for network-level processing can only improve with access to multiple decision thresholds based upon various family attributes, such as family size, F-statistic, and SNR.
Acknowledgements
This work was supported financially and academically by the Air Force Technical Applications Center (AFTAC), the Air Force Institute of Technology (AFIT), and by Los Alamos National Laboratory (LANL). We thank S. Arrowsmith for the data he provided and M. Temple for useful comments.
References
- Cansi, Y. and Le Pichon, A. (2009) Infrasound Event Detection Using the Progressive Multi-Channel Correlation Algorithm. Handbook of Signal Processing in Acoustics, Springer, New York, 1425-1435.
- Shumway, R.H., Kim, S.-E. and Blandford, R.R. (1999) Nonlinear Estimation for Time Series Observed on Arrays. Asymptotics, Nonparametrics, and Time Series, Marcel Dekker, New York, 227-258.
- Cansi, Y. and Klinger, Y. (1997) An Automated Data Processing Method for Mini-Arrays. European-Mediterranean Seismological Centre, Bruyères-le-Châtel.
- Le Pichon, A. and Cansi, Y. (2003) PMCC for Infrasound Data Processing. InfraMatics, 2, 1-9.
- Le Pichon, A. and Cansi, Y. (2003) Progressive Multi-Channel Correlation: Technical Documentation. CTBTO, Vienna.
- Arrowsmith, S., Whitaker, R., Taylor, S., Burlaeu, R., Stump, B., Hedlin, M., Randall, G., Hayward, C. and ReVelle, D. (2008) Regional Monitoring of Infrasound Events Using Multiple Arrays: Application to Utah and Washington State. Geophysical Journal International, 175, 291-300. http://dx.doi.org/10.1111/j.1365-246X.2008.03912.x
- Green, D.N. and Bowers, D. (2010) Estimating the Detection Capability of the International Monitoring System Infrasound Network. Journal of Geophysical Research, 115, D18. http://dx.doi.org/10.1029/2010JD014017
- Le Pichon, A., Blanc, E. and Hauchecorne, A., Eds. (2010) Infrasound Monitoring for Atmospheric Studies. Springer, New York.
- Sklar, B. and Ray, P.K. (2009) Digital Communications: Fundamentals and Applications. Pearson, New York.
- Kay, S.M. (1998) Fundamentals of Statistical Signal Processing: Detection Theory. Vol. 2, Prentice Hall, Upper Saddle River.







