Open Journal of Acoustics
Vol.4 No.2(2014), Article
ID:46927,8
pages
DOI:10.4236/oja.2014.42009
Investigation of SH-Wave Fundamental Modes in Piezoelectromagnetic Plate: Electrically Closed and Magnetically Closed Boundary Conditions
Aaleksey Anatolievich Zakharenko
Department of Physics, International Institute of Zakharenko Waves (IIZWs), Krasnoyarsk, Russia
Email: aazaaz@inbox.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 May 2014; revised 5 June 2014; accepted 12 June 2014
ABSTRACT
It is theoretically considered the propagation (first evidence) of new dispersive shear-horizontal (SH) acoustic waves in the piezoelectromagnetic (magnetoelectroelastic) composite plates. The studied two-phase composites (BaTiO3-CoFe2O4 and PZT-5H-Terfenol-D) possess the piezoelectric phase (BaTiO3, PZT-5H) and the piezomagnetic phase (CoFe2O4, Terfenol-D). The mechanical, electrical, and magnetic boundary conditions applied to both the upper and lower free surfaces of the plate are as follows: the mechanically free, electrically closed, and magnetically closed surfaces. As a result, the fundamental modes of two new dispersive SH-waves recently discovered in book [Zakharenko, A.A. (2012) ISBN: 978-3-659-30943-4] were numerically calculated. It was found that for large values of normalized plate thickness kd (k and d are the wavenumber and plate half-thickness, respectively) the velocities of both the new dispersive SH-waves can approach the nondispersive SH-SAW velocity of the piezoelectric exchange surface Melkumyan (PEESM) wave. It was also discussed that for small values of kd, the experimental study of the new dispersive SH-waves can be preferable in comparison with the nondispersive PEESM wave. The obtained results can be constructive for creation of various technical devices based on (non)dispersive SH-waves and two-phase smart materials. The new dispersive SH-waves propagating in the plates can be also employed for nondestructive testing and evaluation. Also, it is obvious that the plates can be used in technical devices instead of the corresponding bulk samples for further miniaturization.
Keywords:Piezoelectromagnetics, Magnetoelectric Effect, Acoustic SH-Waves in Plates, Wave Dispersion

References
- Berlincourt, D.A., Curran, D.R. and Jaffe, H. (1964) Piezoelectric and Piezomagnetical Materials and Their Function in Transducers. In: Mason, W.P., Ed., Physical Acoustics, Academic Press, New York, 1A, 169-270.
- Annigeri, A.R., Ganesan, N. and Swarnamani, S. (2006) Free Vibrations of Simply Supported Layered and Multiphase Magnetoelectroelastic Cylindrical Shells. Smart Materials and Structures, 15, 459-467. http://dx.doi.org/10.1088/0964-1726/15/2/027
- Aboudi, J. (2001) Micromechanical Analysis of Fully Coupled Electromagnetothermoelastic Multiphase Composites. Smart Materials and Structures, 10, 867-877. http://dx.doi.org/10.1088/0964-1726/10/5/303
- Wang, B.-L. and Mai, Y.-W. (2007) Applicability of the Crack-Face Electromagnetic Boundary Conditions for Fracture of Magnetoelectroelastic Materials. International Journal of Solids and Structures, 44, 387-398. http://dx.doi.org/10.1016/j.ijsolstr.2006.04.028
- Liu, T.J.-Ch. and Chue, Ch.-H. (2006) On the Singularities in a Bimaterial Magnetoelectroelastic Composite Wedge under Antiplane Deformation. Composite Structures, 72, 254-265. http://dx.doi.org/10.1016/j.compstruct.2004.11.009
- Zakharenko, A.A. (2012) On Wave Characteristics of Piezoelectromagnetics. Pramana—Journal of Physics, 79, 275-285.
- Wang, Y.-Z., Li, F.-M., Huang, W.-H., Jiang, X., Wang, Y.-Sh. and Kishimoto, K. (2008) Wave Band Gaps in Two-Dimensional Piezoelectric/Piezomagnetic Phononic Crystals. International Journal of Solids and Structures, 45, 4203-4210. http://dx.doi.org/10.1016/j.ijsolstr.2008.03.001
- Ramirez, F., Heyliger, P.R. and Pan, E. (2006) Free Vibration Response of Two-Dimensional Magnetoelectroelastic Laminated Plates. Journal of Sound and Vibration, 292, 626-644. http://dx.doi.org/10.1016/j.jsv.2005.08.004
- Fiebig, M. (2005) Revival of the Magnetoelectric Effect. Journal of Physics D: Applied Physics, 38, R123-R152. http://dx.doi.org/10.1088/0022-3727/38/8/R01
- Kimura, T. (2012) Magnetoelectric Hexaferrites. Annual Review of Condensed Matter Physics, 3, 93-110. http://dx.doi.org/10.1146/annurev-conmatphys-020911-125101
- Ozgür, ü., Alivov, Ya. and Morkoc, H. (2009) Microwave Ferrites, Part 2: Passive Components and Electrical Tuning. Journal of Materials Science: Materials in Electronics, 20, 911-952. http://dx.doi.org/10.1007/s10854-009-9924-1
- Fiebig, M., Pavlov, V.V. and Pisarev, R.V. (2005) Magnetoelectric Phase Control in Multiferroic Manganites. Journal of the Optical Society of America B, 22, 96-118. http://dx.doi.org/10.1364/JOSAB.22.000096
- Park, Ch.-S. and Priya, Sh. (2012) Broadband/Wideband Magnetoelectric Response. Advances in Condensed Matter Physics (Hindawi Publishing Corporation), 2012, Article ID: 323165, 12 pages.
- Pullar, R.C. (2012) Hexagonal Ferrites: A Review of the Synthesis, Properties and Applications of Hexaferrite Ceramics. Progress in Materials Science, 57, 1191-1334. http://dx.doi.org/10.1016/j.pmatsci.2012.04.001
- Bichurin, M.I., Petrov, V.M. and Petrov, R.V. (2012) Direct and Inverse Magnetoelectric Effect in Layered Composites in Electromechanical Resonance Range: A Review. Journal of Magnetism and Magnetic Materials, 324, 3548-3550. http://dx.doi.org/10.1016/j.jmmm.2012.02.086
- Zakharenko, A.A. (2013) Piezoelectromagnetic SH-SAWs: A Review. Canadian Journal of Pure & Applied Sciences (SENRA Academic Publishers, Burnaby, British Columbia, Canada), 7, 2227-2240.
- Chen, T., Li, S.Y. and Sun, H. (2012) Metamaterials Application in Sensing. Sensors, 12, 2742-2765. http://dx.doi.org/10.3390/s120302742
- Bichurin, M., Petrov, V., Zakharov, A., Kovalenko, D., Yang, S.C., Maurya, D., Bedekar, V. and Priya, S. (2011) Magnetoelectric Interactions in Lead-Based and Lead-Free Composites. Materials, 4, 651-702. http://dx.doi.org/10.3390/ma4040651
- Srinivasan, G. (2010) Magnetoelectric Composites. Annual Review of Materials Research, 40, 153-178. http://dx.doi.org/10.1146/annurev-matsci-070909-104459
- Zhai, J., Xing, Z.P., Dong, S.X., Li, J.F. and Viehland, D. (2008) Magnetoelectric Laminate Composites: An Overview. Journal of the American Ceramic Society, 91, 351-358. http://dx.doi.org/10.1111/j.1551-2916.2008.02259.x
- Nan, C.W., Bichurin, M.I., Dong, S.X., Viehland, D. and Srinivasan, G. (2008) Multiferroic Magnetoelectric Composites: Historical Perspective, Status, and Future Directions. Journal of Applied Physics, 103, Article ID: 031101.
- Eerenstein, W., Mathur, N.D. and Scott, J.F. (2006) Multiferroic and Magnetoelectric Materials. Nature, 442, 759-765. http://dx.doi.org/10.1038/nature05023
- Spaldin, N.A. and Fiebig, M. (2005) The Renaissance of Magnetoelectric Multiferroics. Science, 309, 391-392. http://dx.doi.org/10.1126/science.1113357
- Khomskii, D.I. (2006) Multiferroics: Different Ways to Combine Magnetism and Ferroelectricity. Journal of Magnetism and Magnetic Materials, 306, 1-8. http://dx.doi.org/10.1016/j.jmmm.2006.01.238
- Cheong, S.W. and Mostovoy, M. (2007) Multiferroics: A Magnetic Twist for Ferroelectricity. Nature Materials, 6, 13-20. http://dx.doi.org/10.1038/nmat1804
- Ramesh, R. and Spaldin, N.A. (2007) Multiferroics: Progress and Prospects in Thin Films. Nature Materials, 6, 21-29. http://dx.doi.org/10.1038/nmat1805
- Kimura, T. (2007) Spiral Magnets as Magnetoelectrics. Annual Review of Materials Research, 37, 387-413. http://dx.doi.org/10.1146/annurev.matsci.37.052506.084259
- Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T. and Tokura, Y. (2003) Magnetic Control of Ferroelectric Polarization. Nature, 426, 55-58. http://dx.doi.org/10.1038/nature02018
- Wang, K.F., Liu, J.M. and Ren, Z.F. (2009) Multiferroicity: The Coupling between Magnetic and Polarization Orders. Advances in Physics, 58, 321-448. http://dx.doi.org/10.1080/00018730902920554
- Ramesh, R. (2009) Materials Science: Emerging Routes to Multiferroics. Nature, 461, 1218-1219. http://dx.doi.org/10.1038/4611218a
- Delaney, K.T., Mostovoy, M. and Spaldin, N.A. (2009) Superexchange-Driven Magnetoelectricity in Magnetic Vortices. Physical Review Letters, 102, Article ID: 157203, 4 pages.
- Gopinath, S.C.B., Awazu, K. and Fujimaki, M. (2012) Waveguide-Mode Sensors as Aptasensors. Sensors, 12, 2136-2151. http://dx.doi.org/10.3390/s120202136
- Fert, A. (2008) Origin, Development, and Future of Spintronics (Nobel Lectures). Reviews of Modern Physics, 80, 1517-1530. http://dx.doi.org/10.1103/RevModPhys.80.1517
- Fert, A. (2008) Origin, Development, and Future of Spintronics (Nobel Lectures). Physics—Uspekhi, 51, 1336-1348. [(2008) Uspekhi Phizicheskikh Nauk (Moscow), 178, 1336-1348].
- Chappert, C. and Kim, J.V. (2008) Metal Spintronics: Electronics Free of Charge. Nature Physics, 4, 837-838. http://dx.doi.org/10.1038/nphys1122
- Bibes, M. and Barthélémy, A. (2008) Multiferroics: Towards a Magnetoelectric Memory. Nature Materials, 7, 425-426. http://dx.doi.org/10.1038/nmat2189
- Prellier, W., Singh, M.P. and Murugavel, P. (2005) The Single-Phase Multiferroic Oxides—From Bulk to Thin Film. Journal of Physics: Condensed Matter, 17, R803-R832. http://dx.doi.org/10.1088/0953-8984/17/30/R01
- Bichurin, M.I., Petrov, V.M., Filippov, D.A., Srinivasan, G. and Nan, S.V. (2006) Magnetoelectric Materials. Academia Estestvoznaniya Publishers, Moscow.
- Fetisov, Y.K., Bush, A.A., Kamentsev, K.E., Ostashchenko, A.Y. and Srinivasan, G. (2006) Ferrite-Piezoelectric Multilayers for Magnetic Field Sensors. The IEEE Sensor Journal, 6, 935-938. http://dx.doi.org/10.1109/JSEN.2006.877989
- Srinivasan, G. and Fetisov, Y.K. (2006) Microwave Magnetoelectric Effects and Signal Processing Devices. Integrated Ferroelectrics, 83, 89-98. http://dx.doi.org/10.1080/10584580600949105
- Priya, S., Islam, R.A., Dong, S.X. and Viehland, D. (2007) Recent Advancements in Magnetoelectric Particulate and Laminate Composites. Journal of Electroceramics, 19, 149-166. http://dx.doi.org/10.1007/s10832-007-9042-5
- Grossinger, R., Duong, G.V. and Sato-Turtelli, R. (2008) The Physics of Magnetoelectric Composites. Journal of Magnetism and Magnetic Materials, 320, 1972-1977. http://dx.doi.org/10.1016/j.jmmm.2008.02.031
- Ahn, C.W., Maurya, D., Park, C.S., Nahm, S. and Priya, S. (2009) A Generalized Rule for Large Piezoelectric Response in Perovskite Oxide Ceramics and Its Application for Design of Lead-Free Compositions. Journal of Applied Physics, 105, Article ID: 114108, 6 pages.
- Petrov, V.M., Bichurin, M.I., Laletin, V.M., Paddubnaya, N. and Srinivasan, G. (2003) Modeling of Magnetoelectric Effects in Ferromagnetic/Piezoelectric Bulk Composites. Proceedings of the 5th International Conference on Magnetoelectric Interaction Phenomena in Crystals, MEIPIC-5, Sudak, 21-24 September, 65-70. (arXiv:cond-mat/0401645).
- Harshe, G., Dougherty, J.P. and Newnham, R.E. (1993) Theoretical Modelling of 3-0/0-3 Magnetoelectric Composites. International Journal of Applied Electromagnetics in Materials, 4, 161-171.
- Chu, Y.H., Martin, L.W., Holcomb, M.B. and Ramesh, R. (2007) Controlling Magnetism with Multiferroics. Materials Today, 10, 16-23. http://dx.doi.org/10.1016/S1369-7021(07)70241-9
- Schmid, H. (1994) Magnetic Ferroelectric Materials. Bulletin of Materials Science, 17, 1411-1414. http://dx.doi.org/10.1007/BF02747238
- Ryu, J., Priya, S., Uchino, K. and Kim, H.E. (2002) Magnetoelectric Effect in Composites of Magnetostrictive and Piezoelectric Materials. Journal of Electroceramics, 8, 107-119. http://dx.doi.org/10.1023/A:1020599728432
- Fang, D., Wan, Y.P., Feng, X. and Soh, A.K. (2008) Deformation and Fracture of Functional Ferromagnetics. ASME Applied Mechanics Review, 61, Article ID: 020803, 23 pages.
- Sihvola, A. (2007) Metamaterials in Electromagnetics. Metamaterials, 1, 2-11. http://dx.doi.org/10.1016/j.metmat.2007.02.003
- Hill (Spaldin), N.A. (2000) Why Are There So Few Magnetoelectric Materials? Journal of Physical Chemistry B, 104, 6697-6709.
- Smolenskii, G.A. and Chupis, I.E. (1982) Ferroelectromagnets. Soviet Physics Uspekhi (Uspekhi Phizicheskikh Nauk, Moscow), 25, 475-493.
- Zakharenko, A.A. (2012) Thirty Two New SH-Waves Propagating in PEM Plates of Class 6 mm. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 162 pages.
- Zakharenko, A.A. (2010) Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 84 pages.
- Zakharenko, A.A. (2012) Twenty Two New Interfacial SH-Waves in Dissimilar PEMs. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 148 pages.
- Dieulesaint, E. and Royer, D. (1980) Elastic Waves in Solids: Applications to Signal Processing. Translated by Bastin, A. and Motz, M., Chichester [English], J. Wiley, New York, 511 pages.
- Lardat, C., Maerfeld, C. and Tournois, P. (1971) Theory and Performance of Acoustical Dispersive Surface Wave Delay Lines. Proceedings of the IEEE, 59, 355-368. http://dx.doi.org/10.1109/PROC.1971.8177
- Nye, J.F. (1989) Physical Properties of Crystals. Their Representation by Tensors and Matrices. Clarendon Press, Oxford, 385 pages.
- Auld, B.A. (1990) Acoustic Fields and Waves in Solids. Volumes I and II (Set of Two Volumes). 2nd Edition, Krieger Publishing Company, Malabar, 878 pages.
- Alshits, V.I., Darinskii, A.N. and Lothe, J. (1992) On the Existence of Surface Waves in Half-Infinite Anisotropic Elastic Media with Piezoelectric and Piezomagnetic Properties. Wave Motion, 16, 265-283. http://dx.doi.org/10.1016/0165-2125(92)90033-X
- Melkumyan, A. (2007) Twelve Shear Surface Waves Guided by Clamped/Free Boundaries in Magnetoelectroelastic Materials. International Journal of Solids and Structures, 44, 3594-3599. http://dx.doi.org/10.1016/j.ijsolstr.2006.09.016
- Ribichini, R., Cegla, F., Nagy, P.B. and Cawley, P. (2010) Quantitative Modeling of the Transduction of Electromagnetic Acoustic Transducers Operating on Ferromagnetic Media. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 57, 2808-2817. http://dx.doi.org/10.1109/TUFFC.2010.1754
- Thompson, R.B. (1990) Physical Principles of Measurements with EMAT Transducers. In: Mason, W.P. and Thurston, R.N., Eds., Physical Acoustics, Vol. 19, Academic Press, New York, 157-200.
- Hirao, M. and Ogi, H. (2003) EMATs for Science and Industry: Noncontacting Ultrasonic Measurements. Kluwer Academic, Boston.
2. Theory and Results
First of all, it is necessary to mention the high symmetry propagation directions for the transversely isotropic piezoelectromagnetic materials of class 6 mm. In these propagation directions, the propagation of the SH-waves possessing the anti-plane polarization must be coupled with both the electrical and magnetic potentials. This means that such propagation directions can also support the propagation of the purely mechanical Lamb waves possessing the in-plane polarization. As a result, this report has no interest in the propagation of purely mechanical Lamb waves. So, the wave propagation direction is along the plate surface and perpendicular to both the surface normal and the sixfold symmetry axis of the studied material of class 6 mm. The surface normal and the sixfold symmetry axis must be also perpendicular to each other [53] -[55] . It is possible to state that many such propagation directions can be found. However, the SH-wave speed in such propagation directions must be the same because this is the transversely isotropic case. Note that the high symmetry propagation directions are well-known and can be also found in [56] [57] . Also, it is worth noting that in the high symmetry propagation direction, the following independent nonzero material parameters exist: the stiffness constant C, piezomagnetic coefficient h, piezoelectric constant e, dielectric permittivity coefficient ε, magnetic permeability coefficient μ, and electromagnetic constant α, where C = C44 = C66, e = e16 = e34, h = h16 = h34, ε = ε11 = ε33, μ = μ11 = μ33, and α = α11 = α33 [53] -[55] , see also the famous books cited in [58] [59] .
The boundary conditions in the case when the treated material simultaneously possesses the piezoelectric, piezomagnetic, and magnetoelectric effects are perfectly described in [60] . To obtain the dispersion relations for the case of the mechanically free, electrically closed, and magnetically closed surfaces of the piezoelectromagnetic plate, the following points must be passed through:
• consider thermodynamic variables and functions;
• write constitutive relations;
• thermodynamically define material constants;
• compose equilibrium equations;
• exploit the electrostatics and magnetostatics in the quasi-static approximation;
• constitute coupled equations of motion in the differential forms;
• represent the tensor form of the equations of motion;
• treat the suitable high symmetry propagation directions for SH-waves;
• find the eigenvalues and the corresponding eigenvectors;
• employ the mechanical, electrical, and magnetic boundary conditions at the upper and lower surfaces of the piezoelectromagnetic plate.
As a result, the corresponding dispersion relations can be obtained for this case of the mechanical, electrical, and magnetic boundary conditions. Following book [53] , the following two dispersion relations for the determination of the velocities Vnew10 and Vnew11 of the tenth and eleventh new SH-waves propagating in the piezoelectromagnetic plate can be written:
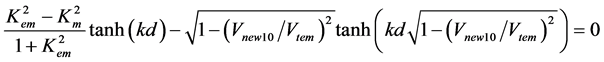 , (1)
, (1)
 . (2)
. (2)
In Equations (1) and (2), the velocities Vnew10 and Vnew11 are numbered similar to those used in [53] to avoid any confusion. It is also central to state that dispersion relations (1) and (2) are valid for calculation of the velocities of the fundamental modes when the velocities Vnew10 and Vnew11 are smaller than the speed Vtem of the shear-horizontal bulk acoustic wave (SH-BAW) coupled with both the electrical and magnetic potentials. The value of the SH-BAW velocity Vtem can be evaluated with the following expression:
 , (3)
, (3)
where r is the mass density of the piezoelectromagnetic plate.
In Expressions (1), (2), and (3), the following material parameter is also present:
 . (4)
. (4)
The material parameter  defined by Expression (4) is called the coefficient of the magnetoelectromechanical coupling (CMEMC). This dimensionless coefficient represents the material characteristic of the two-phase materials. However, in the dispersion relations written above the second dimensionless coefficient denoted by
defined by Expression (4) is called the coefficient of the magnetoelectromechanical coupling (CMEMC). This dimensionless coefficient represents the material characteristic of the two-phase materials. However, in the dispersion relations written above the second dimensionless coefficient denoted by 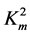 can be found. This coefficient of the magnetomechanical coupling (CMMC) represents a material characteristic of a purely piezomagnetic material and is defined by the following expression:
can be found. This coefficient of the magnetomechanical coupling (CMMC) represents a material characteristic of a purely piezomagnetic material and is defined by the following expression:
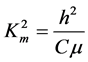 . (5)
. (5)
It is transparent in dispersion relations (1) and (2) that for kd → ¥, both the velocities Vnew10 and Vnew11 of the new dispersive SH-waves in the piezoelectromagnetic plate will approach some nondispersive SH-SAW velocity recently discovered by Melkumyan [61] . This SH-SAW velocity is called the piezoelectric exchange surface Melkumyan (PEESM) wave [6] and can be defined by the following expression:
 . (6)
. (6)
Also, it is possible to discuss in this report that for the case of a very small value of the electromagnetic constant α, this constant can be neglected, namely α = 0. This discussion is missed in [53] . Therefore, Expression (4) for the CMEMC  can be reduced to the following form:
can be reduced to the following form:
 . (7)
. (7)
where 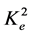 represents the coefficient of the electromechanical coupling (CEMC). It is a material characteristic of a pure piezoelectrics.
represents the coefficient of the electromechanical coupling (CEMC). It is a material characteristic of a pure piezoelectrics.
Using Expression (7) instead of (4), it is possible to write the following definitions instead of the SH-BAW and SH-SAW velocities defined by Expressions (3) and (6), respectively:
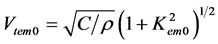 , (8)
, (8)
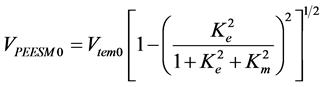 . (9)
. (9)
So, it is now possible to report the obtained results concerning the calculation of the dispersion curves for concrete transversely isotropic composite materials, namely to investigate the dependencies of the velocities Vnew10 and Vnew11 on the normalized half-thickness kd of the piezoelectromagnetic plate, where k and d respectively stand for the wavenumber in the propagation direction and the plate half-thickness. This is the main purpose of this paper. It is possible to briefly discuss the piezoelectromagnetic composites given in Table 1 for comparison. The table lists the material parameters for two famous composites such as BaTiO3-CoFe2O4 and PZT-5H-Terfenol-D. The material parameters of the composites were borrowed from papers [4] -[6] . In the table, one can find that the value of εμ for the BaTiO3-CoFe2O4 composite is an order larger than that for the other composite. Also, both composites have the dominant piezoelectric phase because the CMMC 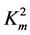 is significantly smaller than the CEMC
is significantly smaller than the CEMC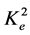 . It is well-known that the PZT-5H-Terfenol-D composite can possess a large value of the electromagnetic constant α that is the characteristic of the magnetoelectric effect. Therefore, to study this composite is preferable in this short report.
. It is well-known that the PZT-5H-Terfenol-D composite can possess a large value of the electromagnetic constant α that is the characteristic of the magnetoelectric effect. Therefore, to study this composite is preferable in this short report.
In the table, the value of the CMEMC for the PZT-5H-Terfenol-D composite is  ~ 0.8. Therefore, the value of the CMEMC for a hypothetic (composite) material graphically studied in Figure 1 is chosen as
~ 0.8. Therefore, the value of the CMEMC for a hypothetic (composite) material graphically studied in Figure 1 is chosen as 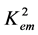 = 0.8. This figure shows the dependence on the second parameter such as
= 0.8. This figure shows the dependence on the second parameter such as  that can be found in dispersion relations (1) and (2). To understand the influence of this parameter on the fundamental mode dispersion relations, the values of
that can be found in dispersion relations (1) and (2). To understand the influence of this parameter on the fundamental mode dispersion relations, the values of 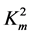 were chosen as follows:
were chosen as follows:  = 0.1, 0.4, and 0.7. In Figure 1, dispersion relations (1) and (2) are shown by the grey and black lines, respectively. It is natural that when the value of
= 0.1, 0.4, and 0.7. In Figure 1, dispersion relations (1) and (2) are shown by the grey and black lines, respectively. It is natural that when the value of 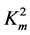 is significantly smaller that the value of
is significantly smaller that the value of 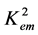 (case of
(case of 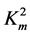 = 0.1 in the figure) both the normalized velocities Vnew10/Vtem and Vnew11/Vtem can be situated well below the SH-BAW velocity Vtem coupled with both the electrical and magnetic potentials. In contrast, the large value of
= 0.1 in the figure) both the normalized velocities Vnew10/Vtem and Vnew11/Vtem can be situated well below the SH-BAW velocity Vtem coupled with both the electrical and magnetic potentials. In contrast, the large value of 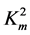 = 0.7, which is slightly below the value of
= 0.7, which is slightly below the value of 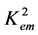 = 0.8, leads to the case when the velocities Vnew10/Vtem and Vnew11/Vtem for the corresponding fundamental modes of the new
= 0.8, leads to the case when the velocities Vnew10/Vtem and Vnew11/Vtem for the corresponding fundamental modes of the new
Table 1 . The material parameters of the piezoelectromagnetic composites. For these parameters there are the following values of the electromagnetic constant α: α2 = 0.0001 εµ [s2/m2] and α2 = 0.01 εµ [s2/m2] for BaTiO3-CoFe2O4 and PZT-5HTerfenol-D, respectively.
dispersive SH-waves are positioned just below Vtem. This already looks like the dispersion relations shown in Figure 2 for the BaTiO3-CoFe2O4 composite possessing the significantly smaller value of the CMEMC  ~ 0.16 listed in the table.
~ 0.16 listed in the table.
Figure 2 shows dispersion relations (1) and (2) for the fundamental modes of the new dispersive SH-waves propagating in the piezoelectromagnetic plates. Two composite materials listed in the table such as BaTiO3-CoFe2O4 and PZT-5H-Terfenol-D are compared. It is clearly seen in Figure 2 that the BaTiO3-CoFe2O4 composite with smaller value of the CMEMC  illuminates the weakly dispersive behaviors of the velocities Vnew10/Vtem and Vnew11/Vtem. However, the values of the velocity Vnew10 at the plate half-thickness kd → 0 can be situated significantly below the value of the SH-BAW velocity Vtem. This is true because the BaTiO3- CoFe2O4 composite has the value of Vtem twice as much compared with the PZT-5H-Terfenol-D composite. This peculiarity manifests that to use plates instead of the corresponding bulk samples can be preferable for investigation of the SH-wave propagation. The plates are also used to further miniaturize various technical devices based on smart materials. It is well-known that the sensitivity of some technical devices (for instant, biological and chemical sensors, delay lines) based on different dispersive and non-dispersive SH-waves can be more significant. It is also flagrant that the piezoelectromagnetic SH-waves can be produced by the electromagnetic
illuminates the weakly dispersive behaviors of the velocities Vnew10/Vtem and Vnew11/Vtem. However, the values of the velocity Vnew10 at the plate half-thickness kd → 0 can be situated significantly below the value of the SH-BAW velocity Vtem. This is true because the BaTiO3- CoFe2O4 composite has the value of Vtem twice as much compared with the PZT-5H-Terfenol-D composite. This peculiarity manifests that to use plates instead of the corresponding bulk samples can be preferable for investigation of the SH-wave propagation. The plates are also used to further miniaturize various technical devices based on smart materials. It is well-known that the sensitivity of some technical devices (for instant, biological and chemical sensors, delay lines) based on different dispersive and non-dispersive SH-waves can be more significant. It is also flagrant that the piezoelectromagnetic SH-waves can be produced by the electromagnetic
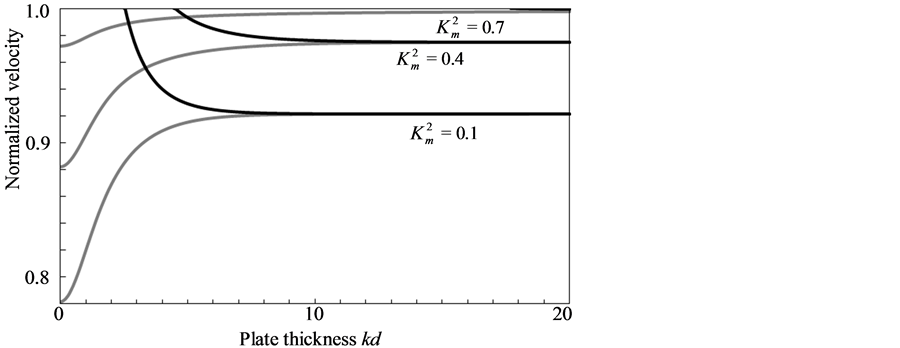
Figure 1. The dispersion relations for the fundamental modes of the new dispersive SH-waves propagating in the piezoelectromagnetic plates. For 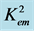 = 0.8, the following values of
= 0.8, the following values of  are used:
are used: 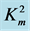 = 0.1, 0.4, and 0.7. The grey and black lines are for dispersion relations (1) and (2), respectively.
= 0.1, 0.4, and 0.7. The grey and black lines are for dispersion relations (1) and (2), respectively.

Figure 2. The fundamental modes of the new dispersive SH-waves propagating in the piezoelectromagnetic plates. The black lines are for the BaTiO3-CoFe2O4 composite and the grey lines are for the PZT-5H-TerfenolD composite.
acoustic transducers (EMATs) [62] . This non-contact method (EMAT) can offer a series of advantages in comparison with the traditional piezoelectric transducers [63] [64] . The results of this short report can be also useful for constitution of technical devices with a higher level of integration such as lab-on-a-chip, etc.
3. Conclusion
The propagation of new dispersive acoustic SH-waves in the transversely isotropic PEM plates was considered. The two-phase PEM composites such as BaTiO3-CoFe2O4 and PZT-5H-Terfenol-D were studied. For the plates, the case of the mechanically free, electrically closed, and magnetically closed surfaces was treated. The fundamental modes of two new dispersive SH-waves were numerically calculated. It was found that for large values of kd, the velocities of both the new dispersive SH-waves can approach the nondispersive SH-SAW velocity of the PEESM wave. For small values of kd, the value of the corresponding new SH-wave in the plate can be situated significantly below the value of the SH-BAW velocity Vtem. This can be convenient for experimental studies of the new dispersive SH-waves propagating even in such PEM materials as BaTiO3-CoFe2O4 in comparison with the nondispersive PEESM wave. It is thought that such new dispersive SH-waves can be also exploited in the nondestructive testing and evaluation. It is natural that various technical devices based on dispersive SH-waves and two-phase smart materials can be constituted, for instance, dispersive wave delay lines.
References
- Berlincourt, D.A., Curran, D.R. and Jaffe, H. (1964) Piezoelectric and Piezomagnetical Materials and Their Function in Transducers. In: Mason, W.P., Ed., Physical Acoustics, Academic Press, New York, 1A, 169-270.
- Annigeri, A.R., Ganesan, N. and Swarnamani, S. (2006) Free Vibrations of Simply Supported Layered and Multiphase Magnetoelectroelastic Cylindrical Shells. Smart Materials and Structures, 15, 459-467. http://dx.doi.org/10.1088/0964-1726/15/2/027
- Aboudi, J. (2001) Micromechanical Analysis of Fully Coupled Electromagnetothermoelastic Multiphase Composites. Smart Materials and Structures, 10, 867-877. http://dx.doi.org/10.1088/0964-1726/10/5/303
- Wang, B.-L. and Mai, Y.-W. (2007) Applicability of the Crack-Face Electromagnetic Boundary Conditions for Fracture of Magnetoelectroelastic Materials. International Journal of Solids and Structures, 44, 387-398. http://dx.doi.org/10.1016/j.ijsolstr.2006.04.028
- Liu, T.J.-Ch. and Chue, Ch.-H. (2006) On the Singularities in a Bimaterial Magnetoelectroelastic Composite Wedge under Antiplane Deformation. Composite Structures, 72, 254-265. http://dx.doi.org/10.1016/j.compstruct.2004.11.009
- Zakharenko, A.A. (2012) On Wave Characteristics of Piezoelectromagnetics. Pramana—Journal of Physics, 79, 275-285.
- Wang, Y.-Z., Li, F.-M., Huang, W.-H., Jiang, X., Wang, Y.-Sh. and Kishimoto, K. (2008) Wave Band Gaps in Two-Dimensional Piezoelectric/Piezomagnetic Phononic Crystals. International Journal of Solids and Structures, 45, 4203-4210. http://dx.doi.org/10.1016/j.ijsolstr.2008.03.001
- Ramirez, F., Heyliger, P.R. and Pan, E. (2006) Free Vibration Response of Two-Dimensional Magnetoelectroelastic Laminated Plates. Journal of Sound and Vibration, 292, 626-644. http://dx.doi.org/10.1016/j.jsv.2005.08.004
- Fiebig, M. (2005) Revival of the Magnetoelectric Effect. Journal of Physics D: Applied Physics, 38, R123-R152. http://dx.doi.org/10.1088/0022-3727/38/8/R01
- Kimura, T. (2012) Magnetoelectric Hexaferrites. Annual Review of Condensed Matter Physics, 3, 93-110. http://dx.doi.org/10.1146/annurev-conmatphys-020911-125101
- Ozgür, ü., Alivov, Ya. and Morkoc, H. (2009) Microwave Ferrites, Part 2: Passive Components and Electrical Tuning. Journal of Materials Science: Materials in Electronics, 20, 911-952. http://dx.doi.org/10.1007/s10854-009-9924-1
- Fiebig, M., Pavlov, V.V. and Pisarev, R.V. (2005) Magnetoelectric Phase Control in Multiferroic Manganites. Journal of the Optical Society of America B, 22, 96-118. http://dx.doi.org/10.1364/JOSAB.22.000096
- Park, Ch.-S. and Priya, Sh. (2012) Broadband/Wideband Magnetoelectric Response. Advances in Condensed Matter Physics (Hindawi Publishing Corporation), 2012, Article ID: 323165, 12 pages.
- Pullar, R.C. (2012) Hexagonal Ferrites: A Review of the Synthesis, Properties and Applications of Hexaferrite Ceramics. Progress in Materials Science, 57, 1191-1334. http://dx.doi.org/10.1016/j.pmatsci.2012.04.001
- Bichurin, M.I., Petrov, V.M. and Petrov, R.V. (2012) Direct and Inverse Magnetoelectric Effect in Layered Composites in Electromechanical Resonance Range: A Review. Journal of Magnetism and Magnetic Materials, 324, 3548-3550. http://dx.doi.org/10.1016/j.jmmm.2012.02.086
- Zakharenko, A.A. (2013) Piezoelectromagnetic SH-SAWs: A Review. Canadian Journal of Pure & Applied Sciences (SENRA Academic Publishers, Burnaby, British Columbia, Canada), 7, 2227-2240.
- Chen, T., Li, S.Y. and Sun, H. (2012) Metamaterials Application in Sensing. Sensors, 12, 2742-2765. http://dx.doi.org/10.3390/s120302742
- Bichurin, M., Petrov, V., Zakharov, A., Kovalenko, D., Yang, S.C., Maurya, D., Bedekar, V. and Priya, S. (2011) Magnetoelectric Interactions in Lead-Based and Lead-Free Composites. Materials, 4, 651-702. http://dx.doi.org/10.3390/ma4040651
- Srinivasan, G. (2010) Magnetoelectric Composites. Annual Review of Materials Research, 40, 153-178. http://dx.doi.org/10.1146/annurev-matsci-070909-104459
- Zhai, J., Xing, Z.P., Dong, S.X., Li, J.F. and Viehland, D. (2008) Magnetoelectric Laminate Composites: An Overview. Journal of the American Ceramic Society, 91, 351-358. http://dx.doi.org/10.1111/j.1551-2916.2008.02259.x
- Nan, C.W., Bichurin, M.I., Dong, S.X., Viehland, D. and Srinivasan, G. (2008) Multiferroic Magnetoelectric Composites: Historical Perspective, Status, and Future Directions. Journal of Applied Physics, 103, Article ID: 031101.
- Eerenstein, W., Mathur, N.D. and Scott, J.F. (2006) Multiferroic and Magnetoelectric Materials. Nature, 442, 759-765. http://dx.doi.org/10.1038/nature05023
- Spaldin, N.A. and Fiebig, M. (2005) The Renaissance of Magnetoelectric Multiferroics. Science, 309, 391-392. http://dx.doi.org/10.1126/science.1113357
- Khomskii, D.I. (2006) Multiferroics: Different Ways to Combine Magnetism and Ferroelectricity. Journal of Magnetism and Magnetic Materials, 306, 1-8. http://dx.doi.org/10.1016/j.jmmm.2006.01.238
- Cheong, S.W. and Mostovoy, M. (2007) Multiferroics: A Magnetic Twist for Ferroelectricity. Nature Materials, 6, 13-20. http://dx.doi.org/10.1038/nmat1804
- Ramesh, R. and Spaldin, N.A. (2007) Multiferroics: Progress and Prospects in Thin Films. Nature Materials, 6, 21-29. http://dx.doi.org/10.1038/nmat1805
- Kimura, T. (2007) Spiral Magnets as Magnetoelectrics. Annual Review of Materials Research, 37, 387-413. http://dx.doi.org/10.1146/annurev.matsci.37.052506.084259
- Kimura, T., Goto, T., Shintani, H., Ishizaka, K., Arima, T. and Tokura, Y. (2003) Magnetic Control of Ferroelectric Polarization. Nature, 426, 55-58. http://dx.doi.org/10.1038/nature02018
- Wang, K.F., Liu, J.M. and Ren, Z.F. (2009) Multiferroicity: The Coupling between Magnetic and Polarization Orders. Advances in Physics, 58, 321-448. http://dx.doi.org/10.1080/00018730902920554
- Ramesh, R. (2009) Materials Science: Emerging Routes to Multiferroics. Nature, 461, 1218-1219. http://dx.doi.org/10.1038/4611218a
- Delaney, K.T., Mostovoy, M. and Spaldin, N.A. (2009) Superexchange-Driven Magnetoelectricity in Magnetic Vortices. Physical Review Letters, 102, Article ID: 157203, 4 pages.
- Gopinath, S.C.B., Awazu, K. and Fujimaki, M. (2012) Waveguide-Mode Sensors as Aptasensors. Sensors, 12, 2136-2151. http://dx.doi.org/10.3390/s120202136
- Fert, A. (2008) Origin, Development, and Future of Spintronics (Nobel Lectures). Reviews of Modern Physics, 80, 1517-1530. http://dx.doi.org/10.1103/RevModPhys.80.1517
- Fert, A. (2008) Origin, Development, and Future of Spintronics (Nobel Lectures). Physics—Uspekhi, 51, 1336-1348. [(2008) Uspekhi Phizicheskikh Nauk (Moscow), 178, 1336-1348].
- Chappert, C. and Kim, J.V. (2008) Metal Spintronics: Electronics Free of Charge. Nature Physics, 4, 837-838. http://dx.doi.org/10.1038/nphys1122
- Bibes, M. and Barthélémy, A. (2008) Multiferroics: Towards a Magnetoelectric Memory. Nature Materials, 7, 425-426. http://dx.doi.org/10.1038/nmat2189
- Prellier, W., Singh, M.P. and Murugavel, P. (2005) The Single-Phase Multiferroic Oxides—From Bulk to Thin Film. Journal of Physics: Condensed Matter, 17, R803-R832. http://dx.doi.org/10.1088/0953-8984/17/30/R01
- Bichurin, M.I., Petrov, V.M., Filippov, D.A., Srinivasan, G. and Nan, S.V. (2006) Magnetoelectric Materials. Academia Estestvoznaniya Publishers, Moscow.
- Fetisov, Y.K., Bush, A.A., Kamentsev, K.E., Ostashchenko, A.Y. and Srinivasan, G. (2006) Ferrite-Piezoelectric Multilayers for Magnetic Field Sensors. The IEEE Sensor Journal, 6, 935-938. http://dx.doi.org/10.1109/JSEN.2006.877989
- Srinivasan, G. and Fetisov, Y.K. (2006) Microwave Magnetoelectric Effects and Signal Processing Devices. Integrated Ferroelectrics, 83, 89-98. http://dx.doi.org/10.1080/10584580600949105
- Priya, S., Islam, R.A., Dong, S.X. and Viehland, D. (2007) Recent Advancements in Magnetoelectric Particulate and Laminate Composites. Journal of Electroceramics, 19, 149-166. http://dx.doi.org/10.1007/s10832-007-9042-5
- Grossinger, R., Duong, G.V. and Sato-Turtelli, R. (2008) The Physics of Magnetoelectric Composites. Journal of Magnetism and Magnetic Materials, 320, 1972-1977. http://dx.doi.org/10.1016/j.jmmm.2008.02.031
- Ahn, C.W., Maurya, D., Park, C.S., Nahm, S. and Priya, S. (2009) A Generalized Rule for Large Piezoelectric Response in Perovskite Oxide Ceramics and Its Application for Design of Lead-Free Compositions. Journal of Applied Physics, 105, Article ID: 114108, 6 pages.
- Petrov, V.M., Bichurin, M.I., Laletin, V.M., Paddubnaya, N. and Srinivasan, G. (2003) Modeling of Magnetoelectric Effects in Ferromagnetic/Piezoelectric Bulk Composites. Proceedings of the 5th International Conference on Magnetoelectric Interaction Phenomena in Crystals, MEIPIC-5, Sudak, 21-24 September, 65-70. (arXiv:cond-mat/0401645).
- Harshe, G., Dougherty, J.P. and Newnham, R.E. (1993) Theoretical Modelling of 3-0/0-3 Magnetoelectric Composites. International Journal of Applied Electromagnetics in Materials, 4, 161-171.
- Chu, Y.H., Martin, L.W., Holcomb, M.B. and Ramesh, R. (2007) Controlling Magnetism with Multiferroics. Materials Today, 10, 16-23. http://dx.doi.org/10.1016/S1369-7021(07)70241-9
- Schmid, H. (1994) Magnetic Ferroelectric Materials. Bulletin of Materials Science, 17, 1411-1414. http://dx.doi.org/10.1007/BF02747238
- Ryu, J., Priya, S., Uchino, K. and Kim, H.E. (2002) Magnetoelectric Effect in Composites of Magnetostrictive and Piezoelectric Materials. Journal of Electroceramics, 8, 107-119. http://dx.doi.org/10.1023/A:1020599728432
- Fang, D., Wan, Y.P., Feng, X. and Soh, A.K. (2008) Deformation and Fracture of Functional Ferromagnetics. ASME Applied Mechanics Review, 61, Article ID: 020803, 23 pages.
- Sihvola, A. (2007) Metamaterials in Electromagnetics. Metamaterials, 1, 2-11. http://dx.doi.org/10.1016/j.metmat.2007.02.003
- Hill (Spaldin), N.A. (2000) Why Are There So Few Magnetoelectric Materials? Journal of Physical Chemistry B, 104, 6697-6709.
- Smolenskii, G.A. and Chupis, I.E. (1982) Ferroelectromagnets. Soviet Physics Uspekhi (Uspekhi Phizicheskikh Nauk, Moscow), 25, 475-493.
- Zakharenko, A.A. (2012) Thirty Two New SH-Waves Propagating in PEM Plates of Class 6 mm. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 162 pages.
- Zakharenko, A.A. (2010) Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 84 pages.
- Zakharenko, A.A. (2012) Twenty Two New Interfacial SH-Waves in Dissimilar PEMs. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbruecken-Krasnoyarsk, 148 pages.
- Dieulesaint, E. and Royer, D. (1980) Elastic Waves in Solids: Applications to Signal Processing. Translated by Bastin, A. and Motz, M., Chichester [English], J. Wiley, New York, 511 pages.
- Lardat, C., Maerfeld, C. and Tournois, P. (1971) Theory and Performance of Acoustical Dispersive Surface Wave Delay Lines. Proceedings of the IEEE, 59, 355-368. http://dx.doi.org/10.1109/PROC.1971.8177
- Nye, J.F. (1989) Physical Properties of Crystals. Their Representation by Tensors and Matrices. Clarendon Press, Oxford, 385 pages.
- Auld, B.A. (1990) Acoustic Fields and Waves in Solids. Volumes I and II (Set of Two Volumes). 2nd Edition, Krieger Publishing Company, Malabar, 878 pages.
- Alshits, V.I., Darinskii, A.N. and Lothe, J. (1992) On the Existence of Surface Waves in Half-Infinite Anisotropic Elastic Media with Piezoelectric and Piezomagnetic Properties. Wave Motion, 16, 265-283. http://dx.doi.org/10.1016/0165-2125(92)90033-X
- Melkumyan, A. (2007) Twelve Shear Surface Waves Guided by Clamped/Free Boundaries in Magnetoelectroelastic Materials. International Journal of Solids and Structures, 44, 3594-3599. http://dx.doi.org/10.1016/j.ijsolstr.2006.09.016
- Ribichini, R., Cegla, F., Nagy, P.B. and Cawley, P. (2010) Quantitative Modeling of the Transduction of Electromagnetic Acoustic Transducers Operating on Ferromagnetic Media. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 57, 2808-2817. http://dx.doi.org/10.1109/TUFFC.2010.1754
- Thompson, R.B. (1990) Physical Principles of Measurements with EMAT Transducers. In: Mason, W.P. and Thurston, R.N., Eds., Physical Acoustics, Vol. 19, Academic Press, New York, 157-200.
- Hirao, M. and Ogi, H. (2003) EMATs for Science and Industry: Noncontacting Ultrasonic Measurements. Kluwer Academic, Boston.


