Open Journal of Acoustics
Vol.3 No.3(2013), Article ID:36743,8 pages DOI:10.4236/oja.2013.33013
Holes Effects in Plane Periodic Multilayered Viscoelastic Media
1Département de Physique, Groupe de Mécanique et des Matériaux (GMM), Université de Ngaoundéré, Ngaoundéré, Cameroun
2Laboratoire Ondes et Milieux Complexes (LOMC), UMR 6294 CNRS, Université du Havre, Le Havre, France
Email: *pierre.marechal@univ-lehavre.fr
Copyright © 2013 Emmanuel Siryabe et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 16, 2013; revised August 16, 2013; accepted August 23, 2013
Keywords: periodic structures; holes; porosity; phononic crystal; forbidden bands; transmission; reflection; attenuation
ABSTRACT
This work deals with the study of the reflection and transmission properties of plane periodic structures composed of N periods (1 ≤ N ≤ 3) in the MHz frequency range. The period consists of two bounded plates presenting a high acoustic impedance contrast one of which is in aluminum, the other is in polyethylene. The longitudinal and transversal attenuations are considered in polyethylene and neglected in aluminum. We take into account the case of emerging holes in the polyethylene layer. Simulations are based on the stiffness matrix method (SMM) developed by Rokhlin. When attenuation is considered in polyethylene, the reflection coefficients are different depending on the insonification side. The comparison of results without or with holes configurations are performed and showed that throughout holes allow the rapid observation of forbidden bands. The attenuation of the whole multilayer is also determined.
1. Introduction
Phononic crystals (PC) are n-dimensional periodic structures (1 £ n £ 3) that are made of at least two materials with different mechanical properties. They are widely studied because of their very interesting properties such as band gaps in their dispersion curves. Many studies on perforated plate systems showed that the absorption performance depends upon the dimensions such as thickness, hole diameter and porosity, the depth of airspace and the number of the perforated plates [1-3]. Recently, the absorption performances of perforated panel systems were estimated by analytical approach [4,5], equivalent electro-acoustic circuit approach [6,7], and experimental approach in the kHz frequency range [8]. The aim of this work is to study the emerging holes effect in a layer constituting a period of a one-dimensional plane periodic structure. In previous studies [9-11], the reflection and transmission properties of N periods (1 < N < 8) of an elementary bilayer stack was studied. Here, the effect of the porosity ratio is investigated in a prospective way on the transmission, reflection and attenuation spectra in the MHz frequency range. The absorption of the system is deduced and evaluated. Theoretically, the reflection coefficient is obtained by using the stiffness matrix method (SMM) developed by Rokhlin, et al. [12], which is proved to be stable numerically, whatever the frequency range and the incidence angle. Two cases of insonification have been studied and showed that if we consider attenuation in one of the constitutive plates, the refection coefficients are different depending on the insonification side while the transmission coefficients are identical [9,10]. Simulations are performed on porous plates is comparison with massive plates. In this view, we consider drilled holes into the thickness of the plate. In Section 2, the studied configuration is described and the theoretical basis is recalled. In Section 3, theoretical transmission, reflection, and attenuation spectra of two configurations are compared and discussed, without and with holes, depending on the insonification side. In the final section, the conclusion and perspectives of this work are presented.
2. Periodic Isotropic Porous Structure
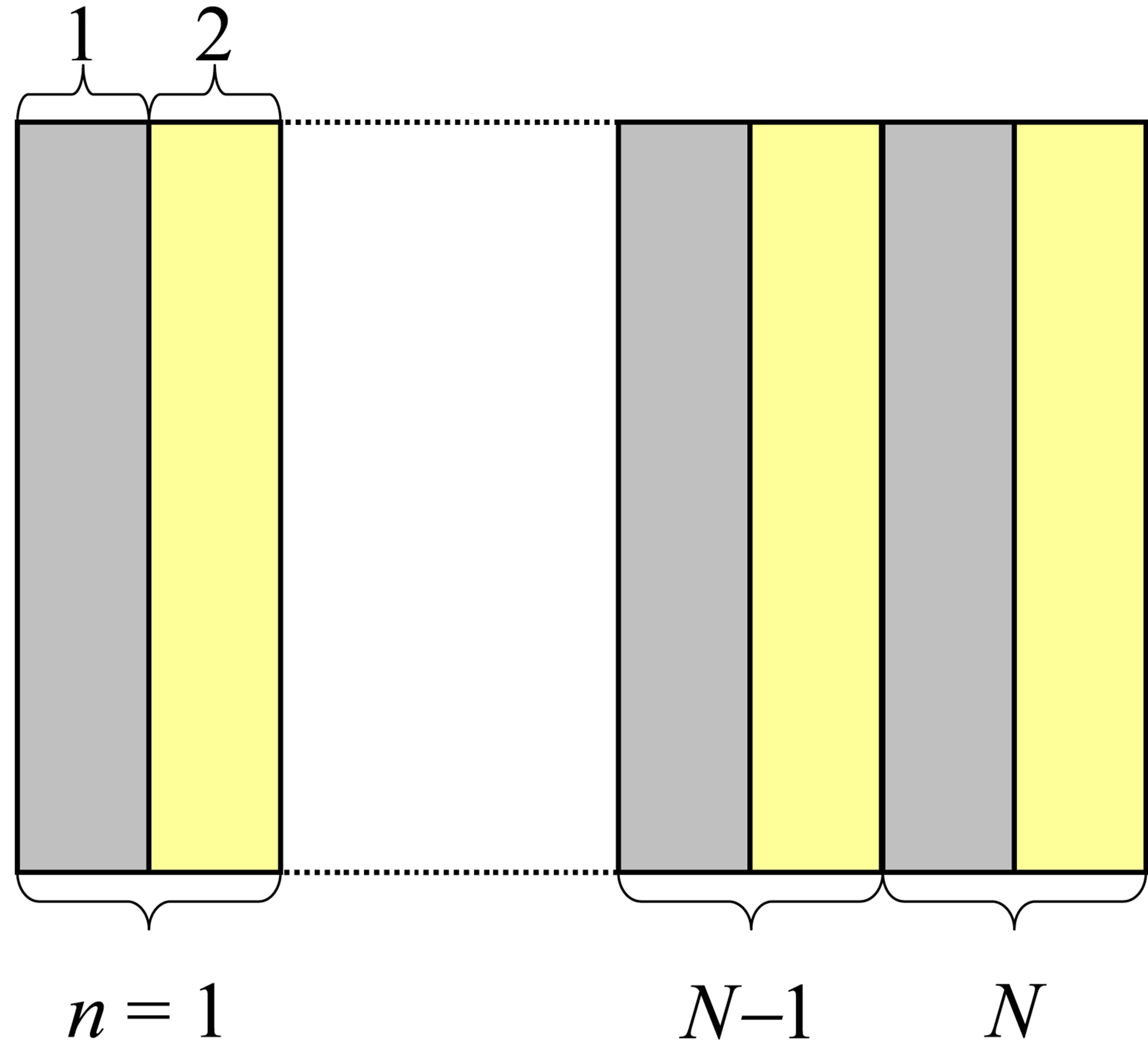
The geometry of the problem (Figure 1(a)) consists in N periods of a stack composed of np isotropic plates. In this study, a period consists in the bonding, supposed to be perfect, of two plates presenting a high acoustic impedance contrast. The studied multilayer structure is constituted of an elementary stack made of np = 2 isotropic plates (bilayer), and the number of periods varies from 1 to 5. Such a periodic structure based on a bilayer elementary stack has been investigated for Bragg backing purpose [13]. The acoustic impedance contrast between the two layers constituting the elementary stack was highlighted as a key parameter for the stopband flatness. In order to reach a high acoustic impedance contrast, we chose a metal/polymer elementary stack: aluminum and polyethylene plates. The acoustic impedance contrast was reinforced by considering drilled holes into the thickness of the polymer plated (Figure 1(b)). These holes allow to lower not only the effective density, but also the effective acoustic velocities in the drilled layer.
2.1. Effect of Porosity on Elastic Isotropic Properties
The effective elastic isotropic properties of composite materials, also known as effective medium theory (EMT), directly results from those of the constitutive materials and their spatial arrangement [14-17]. The effect of porosity ratio was widely investigated and various models were proposed and confronted [18-21]. This section is aimed at evaluating the effect of on the effective elastic properties. The porosities are considered as induced by randomly dispersed drilled holes along the thickness of a layer. In a first order approach, we consider the Voigt model of a perforated plate having mechanical properties X, filled by inclusions having mechanical properties Xi, where X stands for the bulk modulus K, shear modulus G and density r, respectively. The effective mechanical properties Xeff = {Keff, Geff, reff}, are related to those of the matrix X = {K, G, r} and those of the inclusion Xi = {Ki, Gi, ri}:
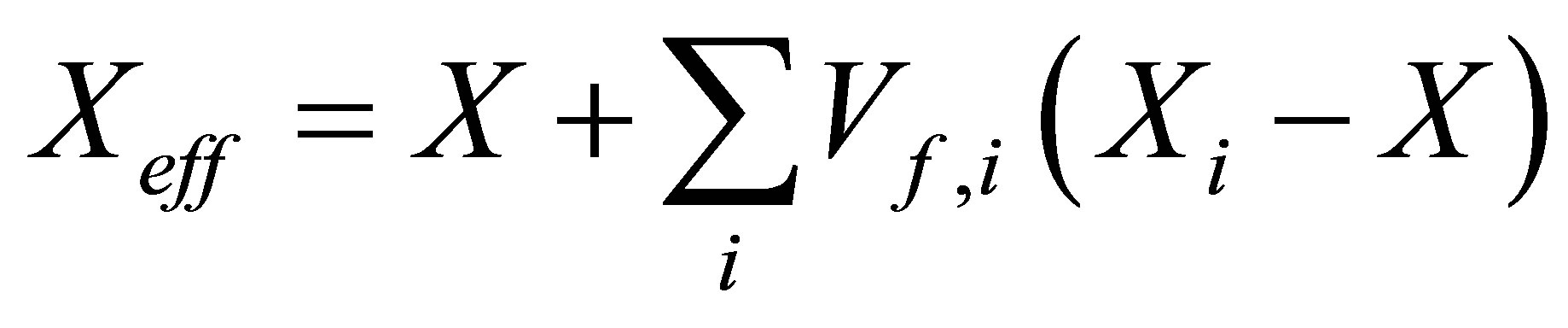 (1)
(1)
where Xi and Vf,i are the mechanical property and the volume fraction of inclusions, respectively. Considering the holes like inclusions, 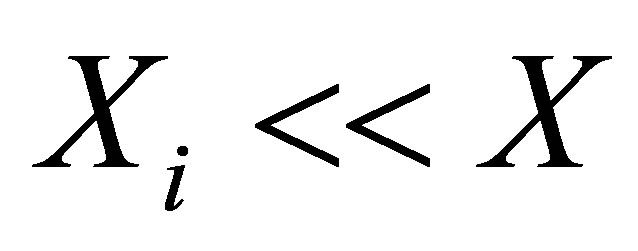 and Equation becomes:
and Equation becomes:
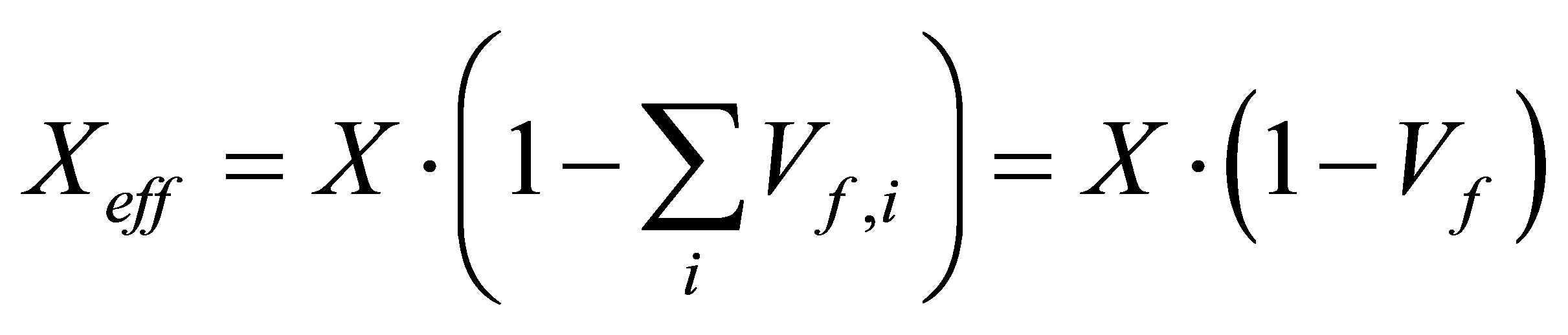 (2)
(2)
where Vf = Vholes/Vplate is the volume fraction of inclusions relatively to the full plate.
The effective elastic constants Xeff = {Keff, Geff, reff} (equation (2)) can be converted into Yeff = {Eeff, neff, reff} (equation ), where Eeff is the effective Young modulus, neff is the effective Poisson’s ratio and reff is the effective density, respectively:
 (a)
(a)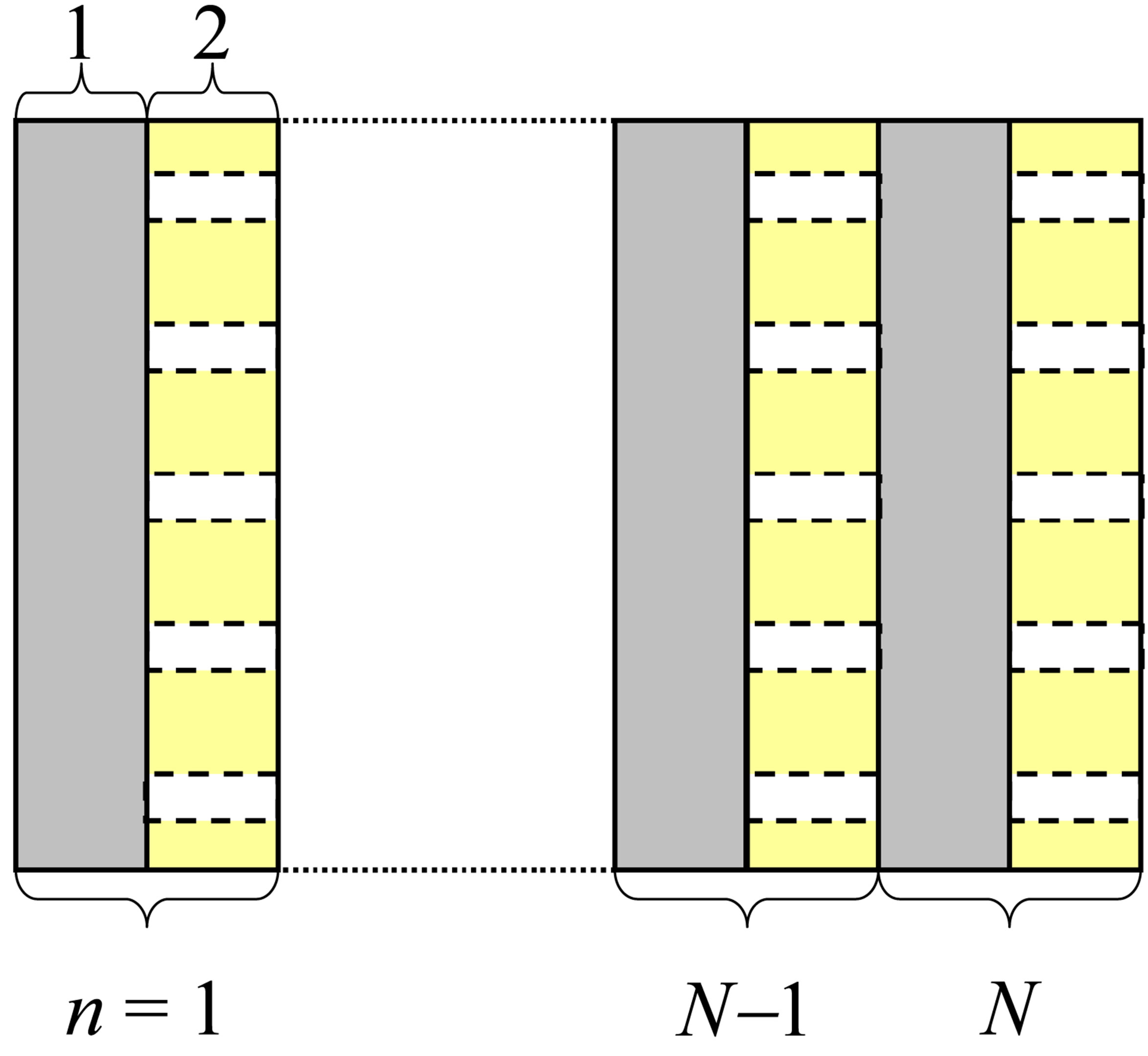 (b)
(b)
Figure 1. Multilayer structure constituted of N periods of an elementary stack of np = 2 layers (a) without porosities and (b) with a controlled porosity ratio Vf.
 (3)
(3)
The effective acoustic velocities Ceff = {CLeff, CTeff} are then deduced, where CLeff is the effective longitudinal phase velocity and CTeff is the effective transverse phase velocity. Using the effective elastic properties Yeff = {Eeff, neff, reff} obtained in equation (3), the effective acoustic properties of perforated plates are obtained:
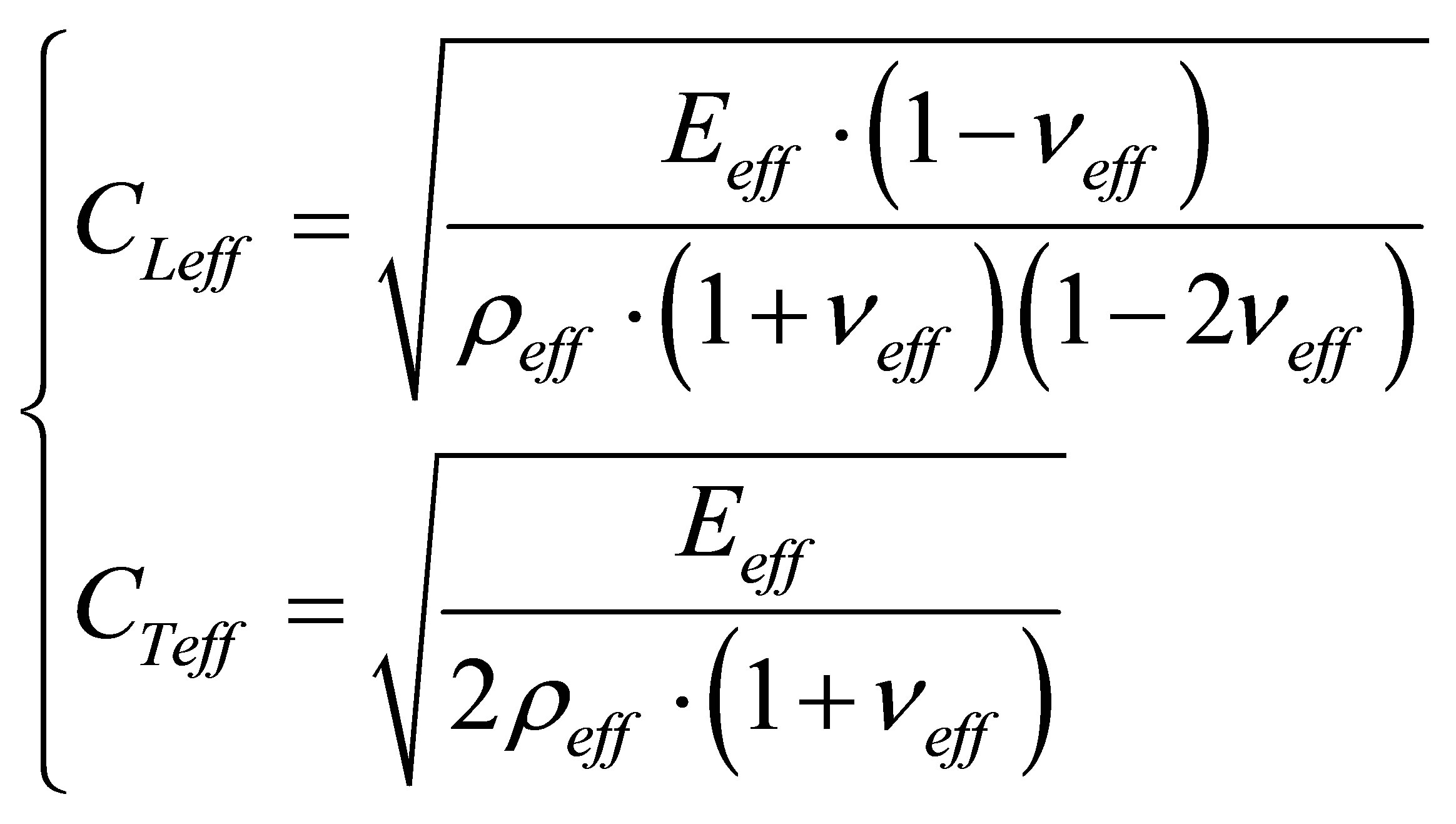 (4)
(4)
This approach, based on the Voigt model (equation (2)) is compared to improved homogenization approaches, considering various assumptions, such as the homogenization model developed by Gaunaurd, et al. [22,23], considering the volume fraction Vf of spherical inclusions (G-sph). These expressions are very close to the upper bounds formulated by Hashin and Shtrikman for the isotropic case (HS-iso) in 1963 [24] and for the transverse isotropic (orthotropic) case (HS-ort) in 1965 [25], respectively. In the case of air inclusions, the filling medium elastic constant can be neglected relatively to those of the matrix dense material (Table 1). These Hashin and Shtrikman homogenization formulas [26] were widely studied and discussed for various configurations [27-30]. In a general way, depending on the homogenization model, the effective elastic constants of the material can be written as:
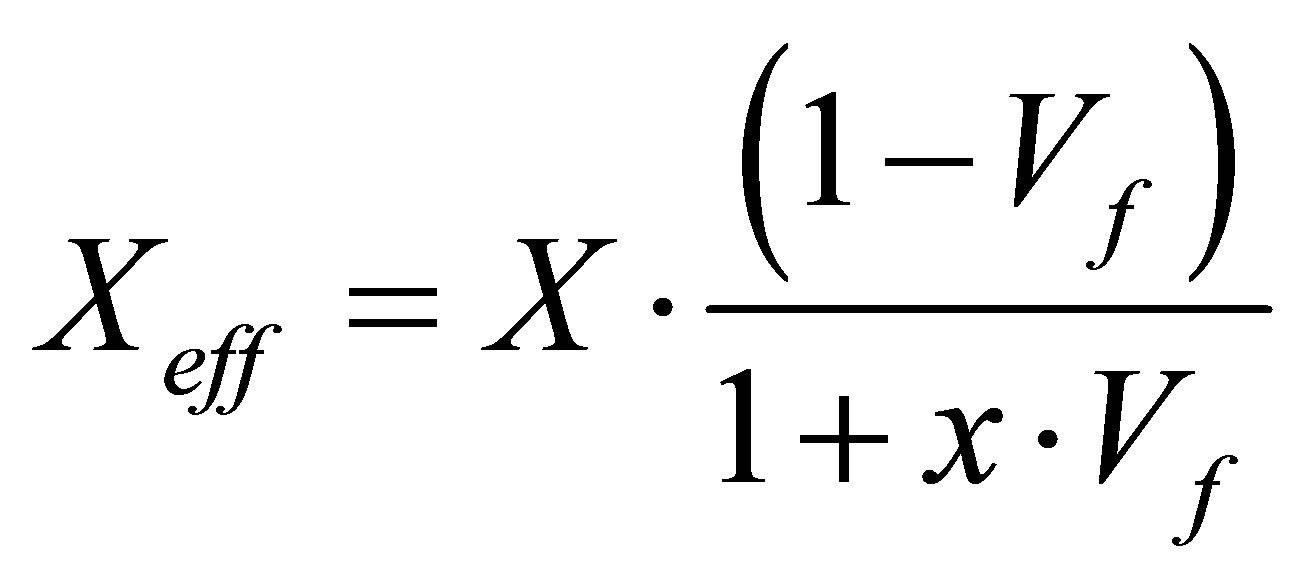 (5)
(5)
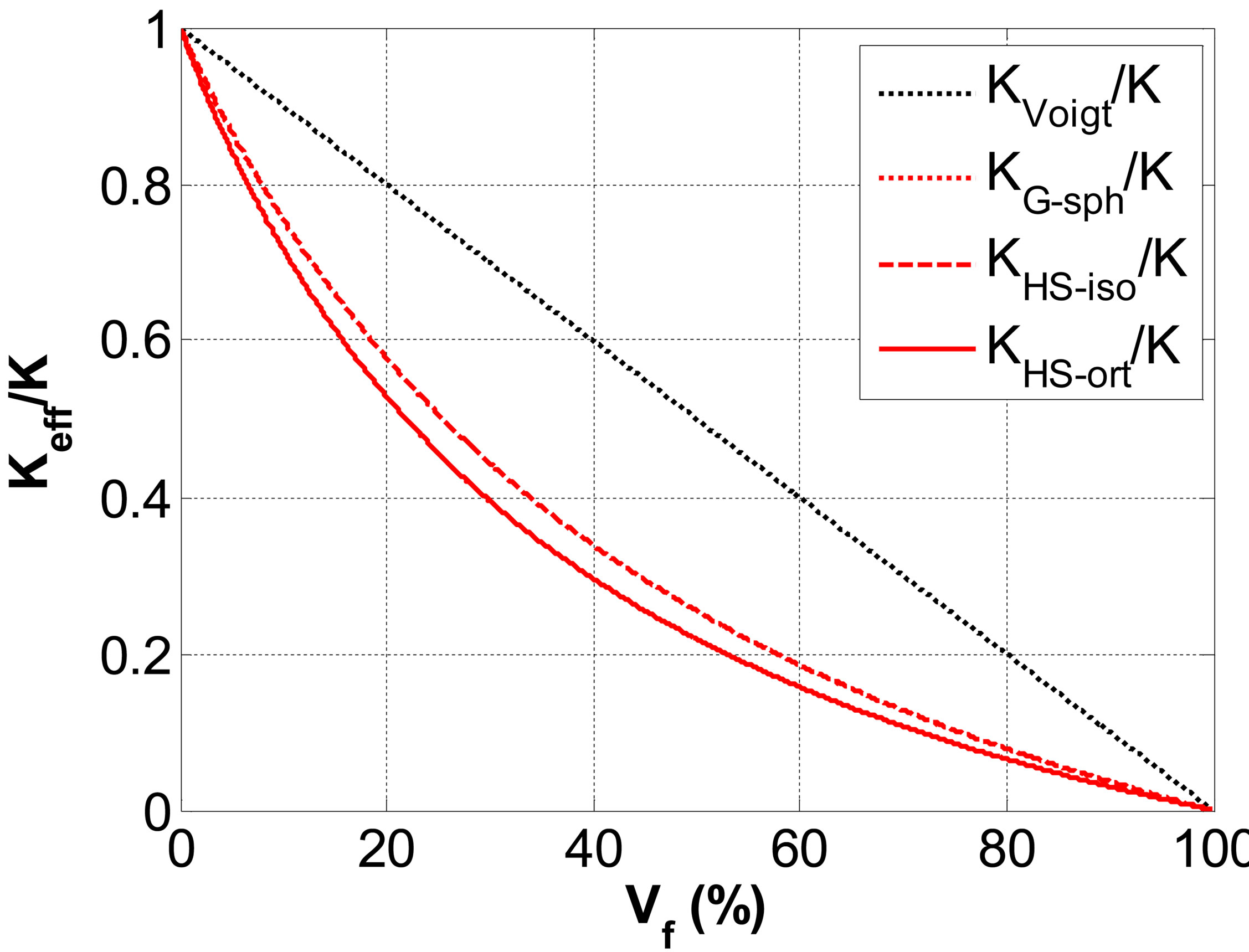
where, x = {k, g, r} is either a constant or a function depending on the homogenization model, associated to the elastic properties of the matrix X = {K, G, r}. For example, in the case of the Gaunaurd’s homogenization model (Table 1), one obtains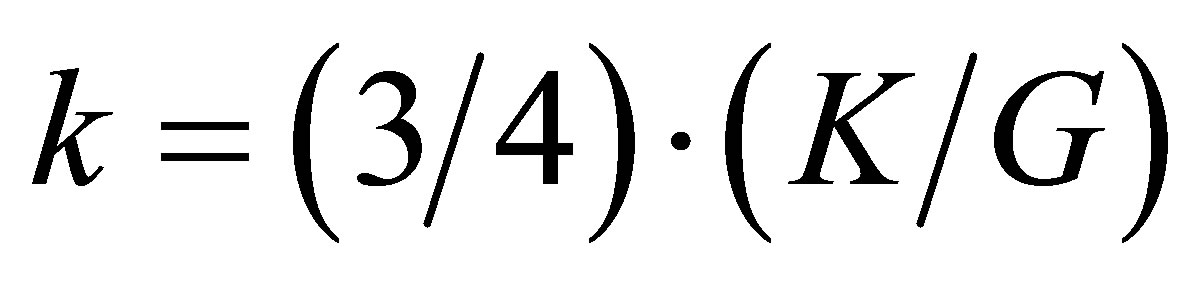 , g = 2/3, and r = 0. These homogenization models are compared through the plots of the normalized elastic constants Keff/K (Figure 2(a)) and Geff/G (Figure 2(b)) as a function of the void volume fraction Vf, in the case where the bulk to shear modulus ratio K/G = 8/3, corresponding to a Poisson’s ratio n = 1/3.
, g = 2/3, and r = 0. These homogenization models are compared through the plots of the normalized elastic constants Keff/K (Figure 2(a)) and Geff/G (Figure 2(b)) as a function of the void volume fraction Vf, in the case where the bulk to shear modulus ratio K/G = 8/3, corresponding to a Poisson’s ratio n = 1/3.
2.2. Orthotropic Composite Homogenization
In this study, the porosity ratio is induced by drilled holes, considered as cylindrical inclusions of air. Therefore, the orthotropic composite homogenization is the adequate formulation in order to evaluate the acoustic properties of a perforated plate. As a result of equations (3)-(5), the effective elastic constants Yeff = {Eeff, neff, reff} are, respectively:

Table 1. Effective elastic properties according to the homogenization models.
 (a)
(a)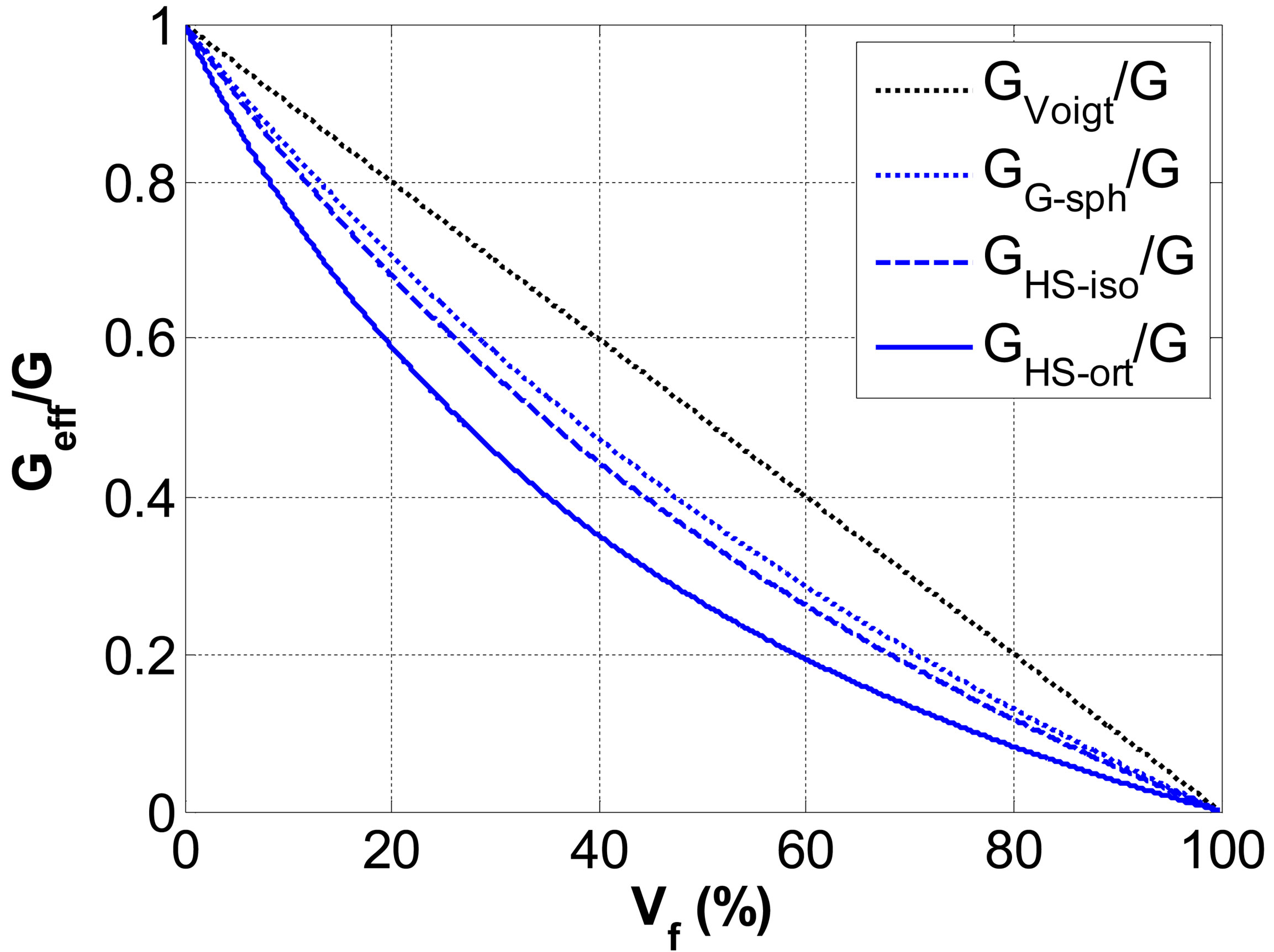 (b)
(b)
Figure 2. Normalized effective elastic properties according to the homogenization model (Voigt; G-sph; HS-iso; HSort), as a function of the volume fraction of porosity Vf: (a) normalized effective bulk modulus Keff/K and (b) normalized effective shear modulus Geff/G.
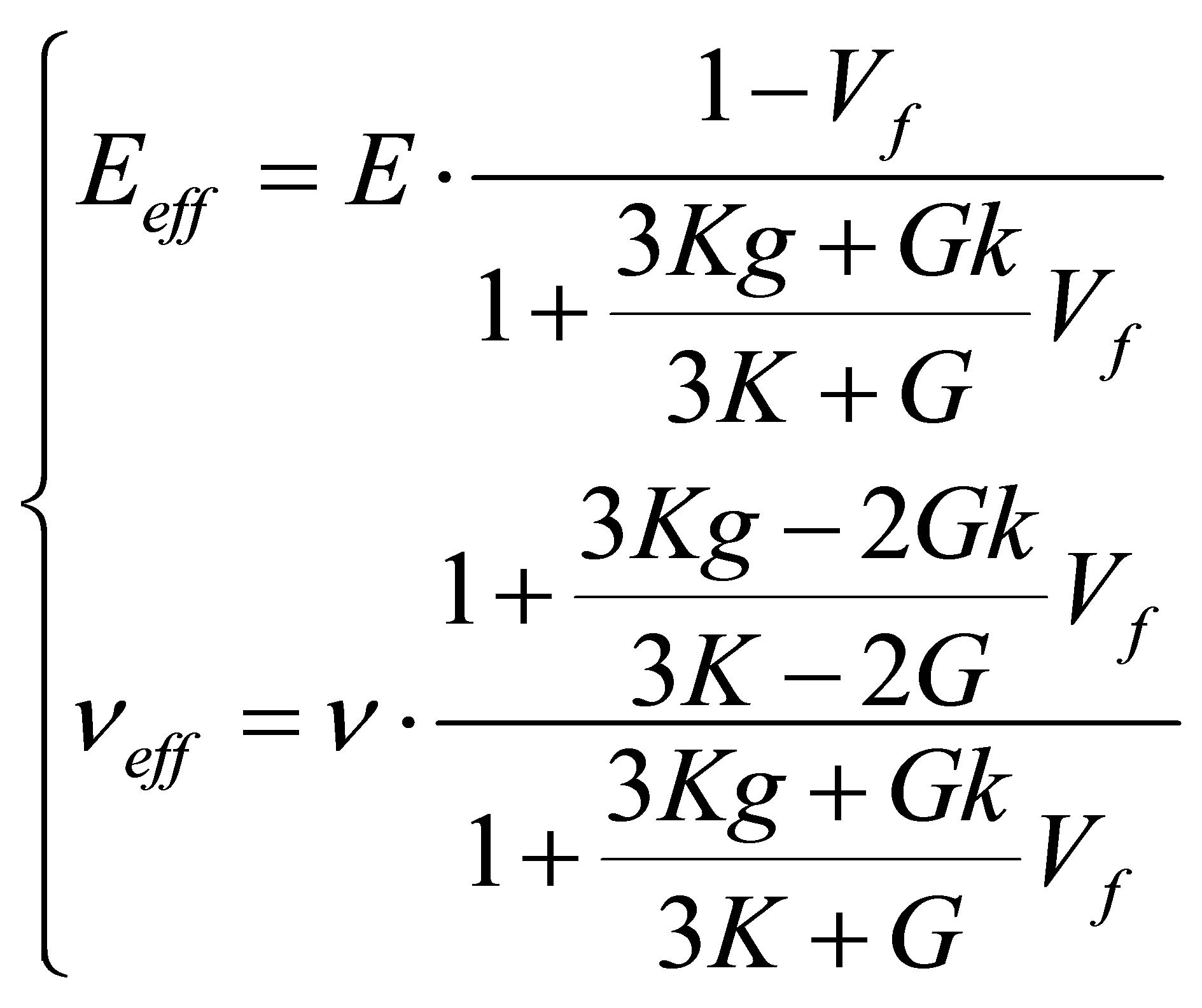 (6)
(6)
The normalized effective elastic constants

(equation (6)) are directly related to the bulk to shear modulus ratio K/G, which is itself a function of the Poisson’s ratio n. These normalized elastic constants Yeff/Y are plotted for n = 1/3 (Figure 3(a)), as a function of the void volume fraction Vf. This result (equation (6)) is used as input data to deduce the effective acoustic velocities Ceff = {CLeff, CTeff} (equation (4)) as a function of the volume fraction of vaccum Vf:
 (7)
(7)
 (a)
(a)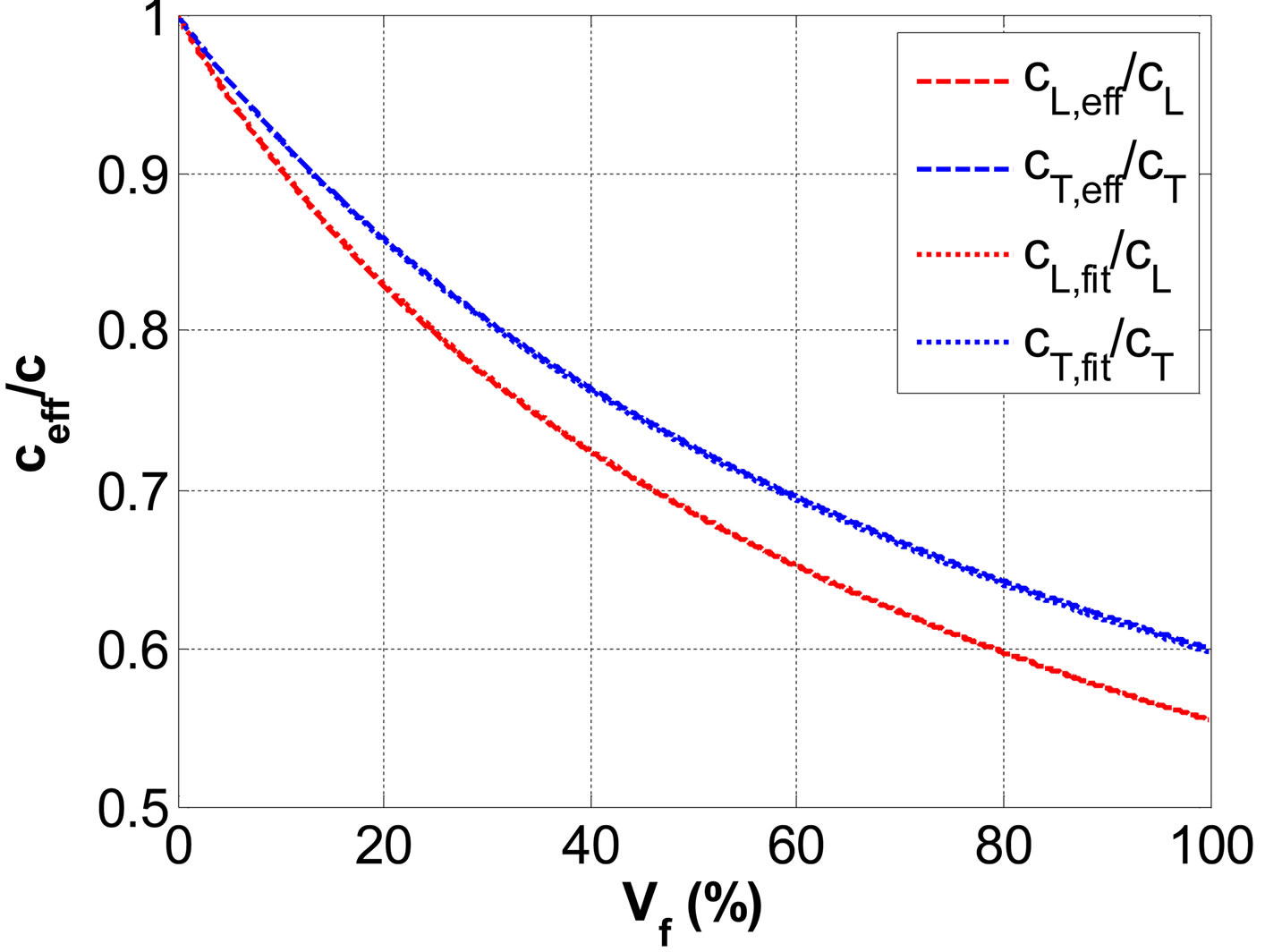 (b)
(b)
Figure 3. Effective elastic properties deduced from the HSort homogenization model: (a) normalized Young modulus, Poisson’s ratio and density (Eeff, neff, reff) and (b) normalized effective logitudinal velocities (CLeff, CTeff).
For a material having a Poisson’s ratio for n = 1/3, a fitting approach (Figure 3(b)) gives:
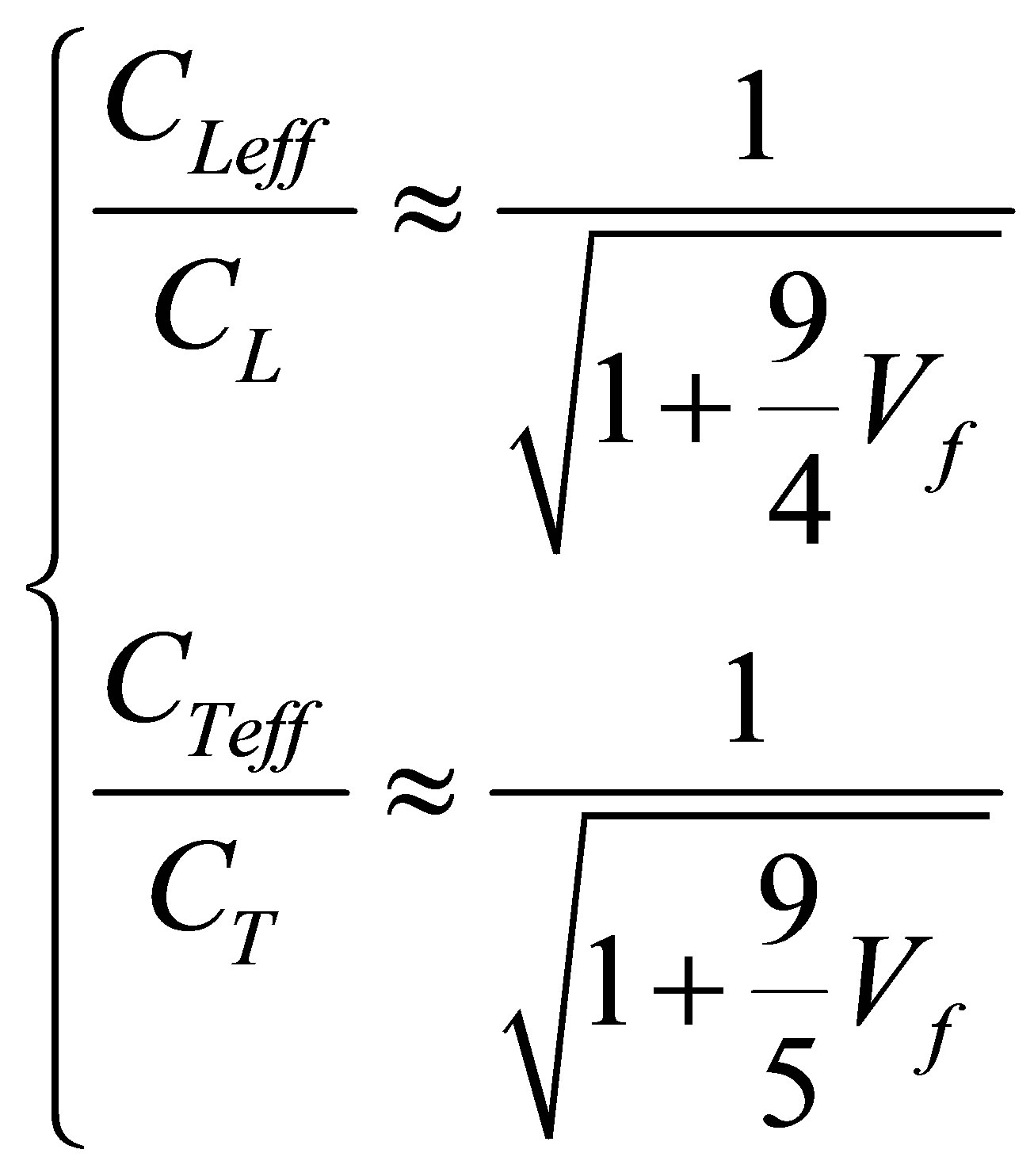 (8)
(8)
2.3. Wave Propagation through Multilayer Structure
In this subsection, the theoretical transmission, reflection, and attenuation spectra of plane multilayer structures are reminded. Without viscoelasticity, there is no attenuation and the energy conservation lead to |T|2 + |R|2 = 1. The consideration of viscoelasticity in one of the constitutive layers conduct to the loss of reciprocity of the reflection coefficient from one side to the other. We denote as Rd the reflection coefficient when the structure is insonified directly (Figure 4(a)) and Rr the reflection coefficient when it is insonified reversely (Figure 4(b)). The transmission coefficient is denoted as T. As illustrated by equation and Figure 4, the completion of the energy
 (a)
(a)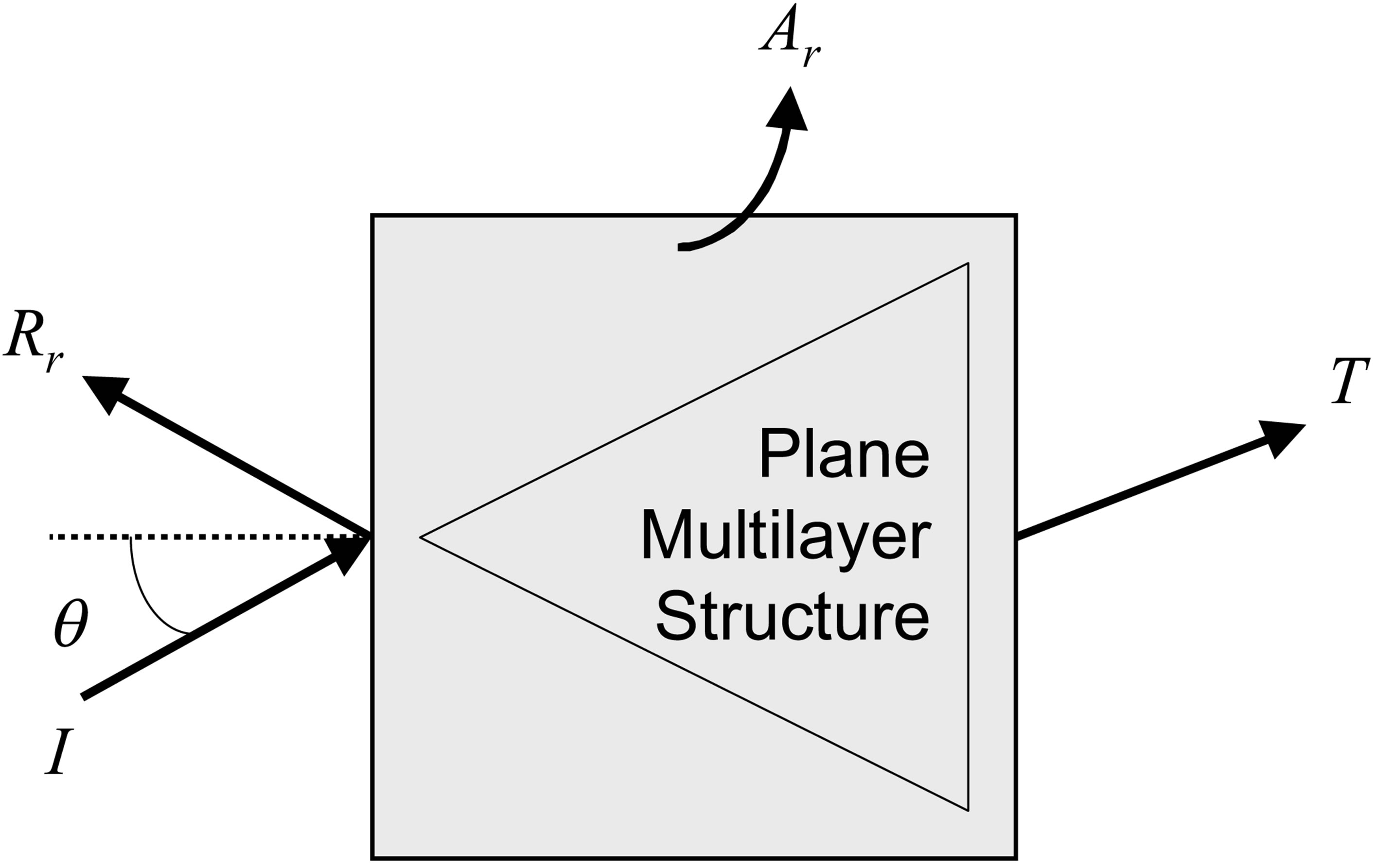 (b)
(b)
Figure 4. Scheme of the non-reversal properties of a periodic viscoelastic structure (a) for a direct insonification, resulting in (Rd, T, Ad) and (b) for a reverse insonification, resulting in (Rr, T, Ar).
conservation associated to the either direct (index d) or reverse (index r) insonification side results in an attenuation coefficient Ad or Ar:
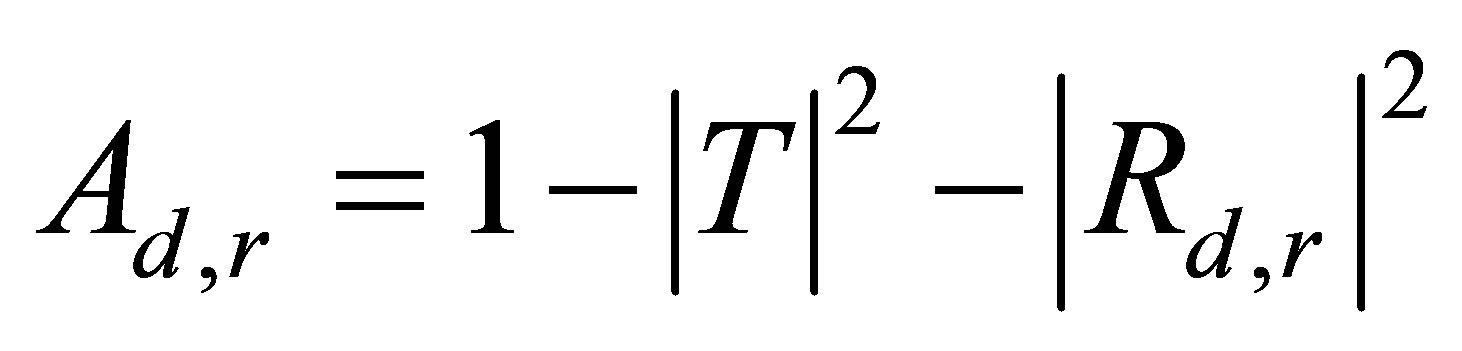 (9)
(9)
stiffness matrix method.
Those coefficients are obtained using the stiffness matrix method (SMM) developed by Rokhlin, et al. [12]. It defines the 4 × 4 compliance matrix for period n:
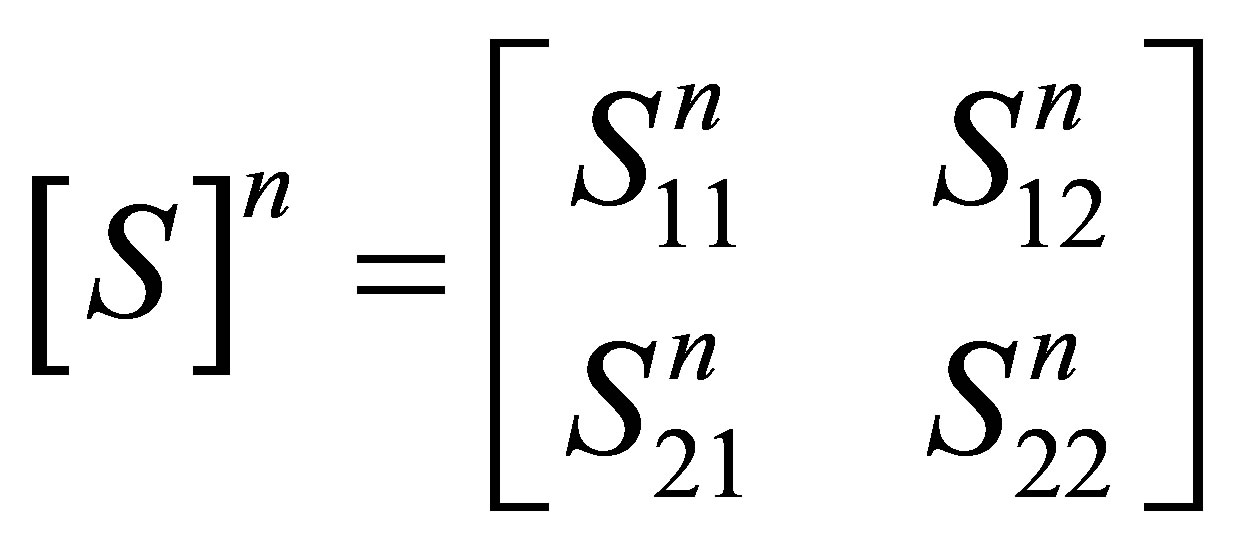 (10)
(10)
where Sij are 2 × 2 submatrices.
The submatrices Sij for N periods are deduced from the ones for (N - 1) periods and those of an additional nth layer by the following recursive relationships:
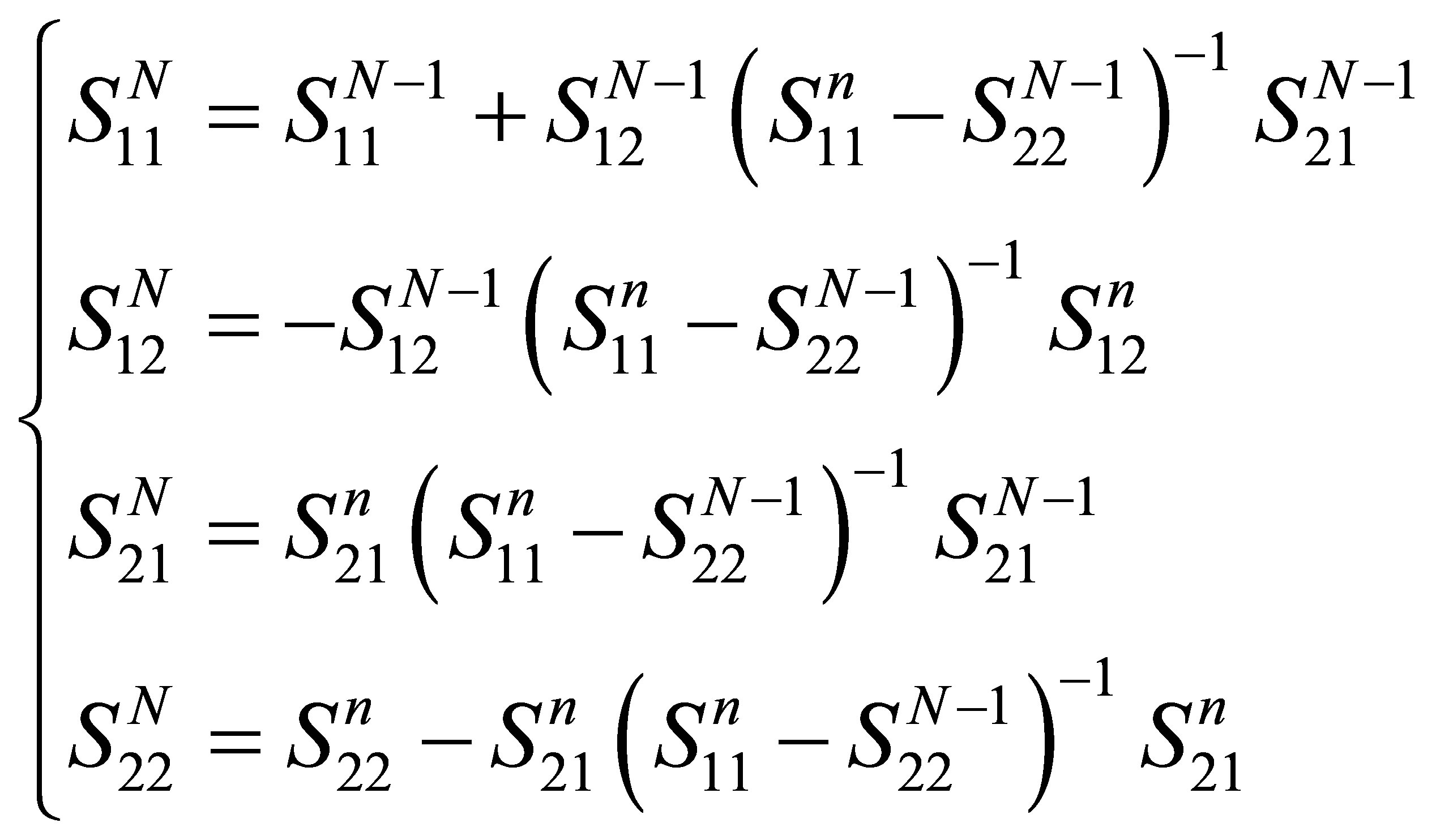 (11)
(11)
The transmission coefficient (T) and the direct and reverse reflection coefficients, Rd and Rr, are illustrated in Figures 4(a) and (b), respectively. They are expressed as functions of the (2, 2) elements of the submatrices Sij extracted from the global compliance matrix SN in the following relationships:

and ρF and CF are the density and wave velocity in the surrounding fluid medium, i.e. water.
3. Results
In this section, the theoretical reflection and transmission spectra (equation (12)) are plotted depending on the insonification side of the multilayer structure (Figure 4). The characteristics of each layer composing a period and those of the surrounding medium are summarized in Table 2. The calculated effective acoustic properties of the perforated polyethylene plate are calculated according to equation (7). The considered porosity ratio was evaluated on the basis of randomly dispersed drilled holes in the thickness of the polyethylene plate. The drilling diameter was considered small compared to the plate thickness. The chosen volume fraction is Vf = 20%. Hereafter, these constitutive layers are denoted as AL, PE and PEp, for aluminum, polyethylene and perforated polyethylene, respectively. Hereafter, the transmission, reflection or attenuation coefficients exhibits extrema at multiples of the first thickness mode defined as , where DfAL » 800 kHz, DfPE » 295 kHz, and DfPEp » 245 kHz, for the AL, PE and PEp plates respectively. These characteristics are observed and discussed (Figures 5-8) in the 0.75 - 3.25 MHz frequency
, where DfAL » 800 kHz, DfPE » 295 kHz, and DfPEp » 245 kHz, for the AL, PE and PEp plates respectively. These characteristics are observed and discussed (Figures 5-8) in the 0.75 - 3.25 MHz frequency
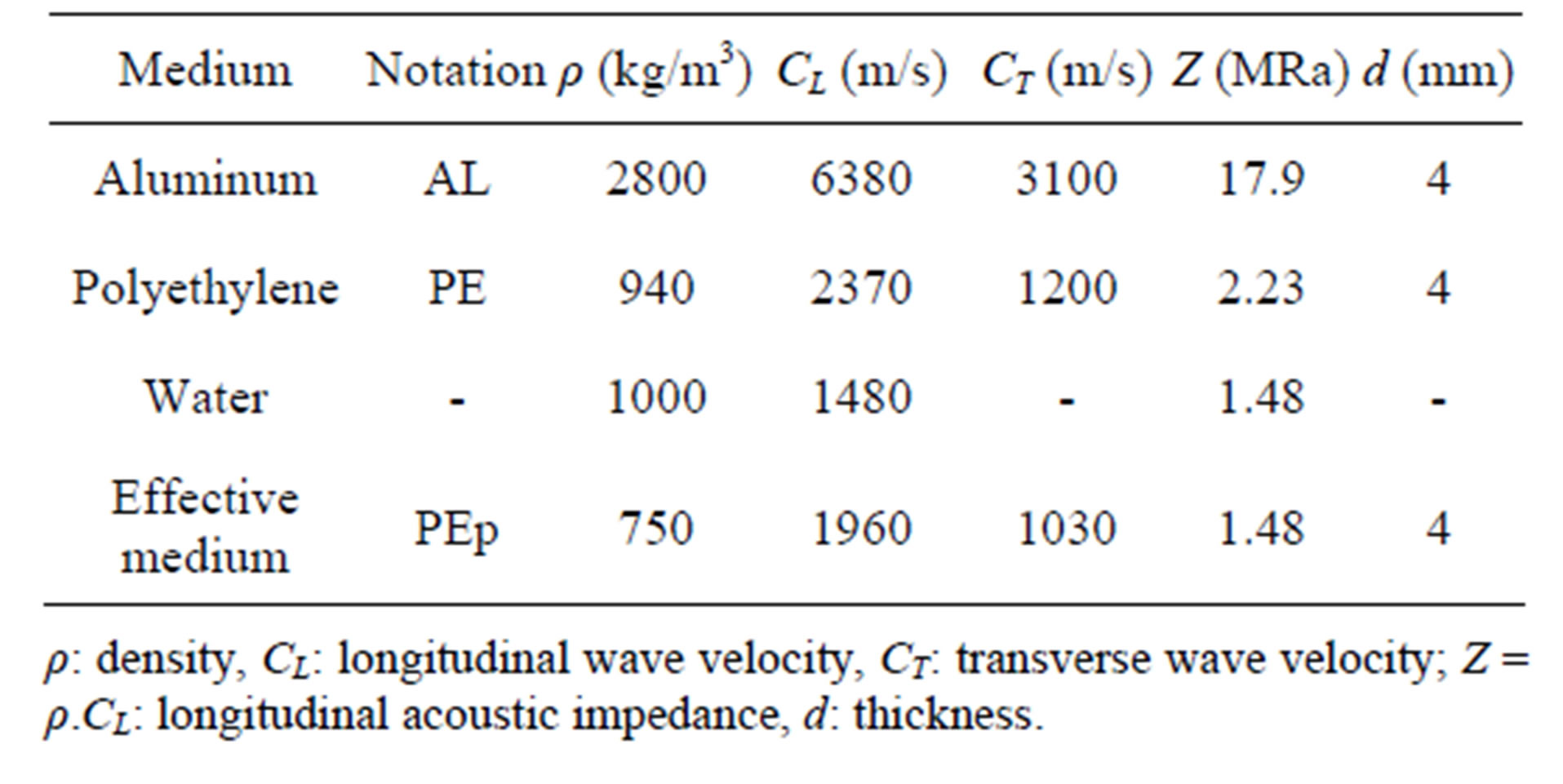
Table 2. Acoustics properties of each layer composing a period [9].
range. This frequency range corresponds to a 110% relative bandwidth of a 2.25 MHz center frequency transducer used for experimental purpose in preliminary works [9-11].
3.1. Viscoelasticity as Limiting Factor of the Periodicity Effect
A calculation without losses would show an identical reflection spectrum, whatever the direction: direct or reverse due to their complex conjugate numerators [31]. In the present case, we take into account the longitudinal absorption in polyethylene, by considering the longitudinal wave velocity as a complex that can be expressed as: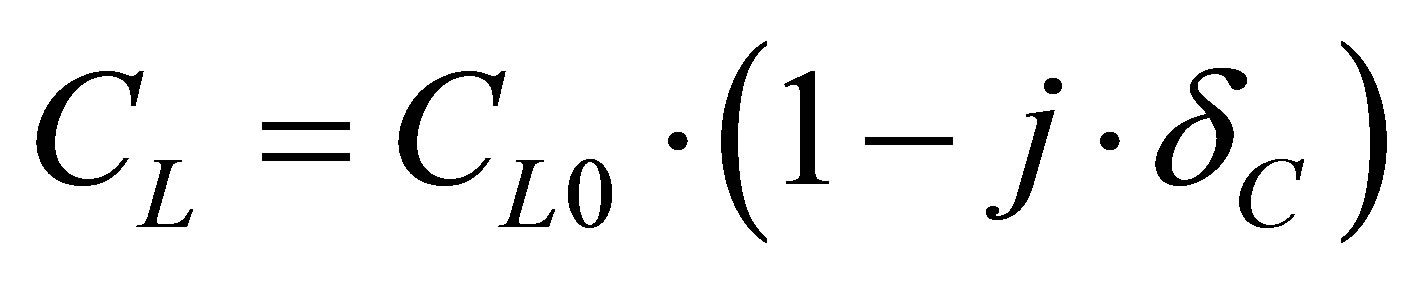 , what is a common assumption for solid materials. This implies that attenuation is linearly depending on the frequency as
, what is a common assumption for solid materials. This implies that attenuation is linearly depending on the frequency as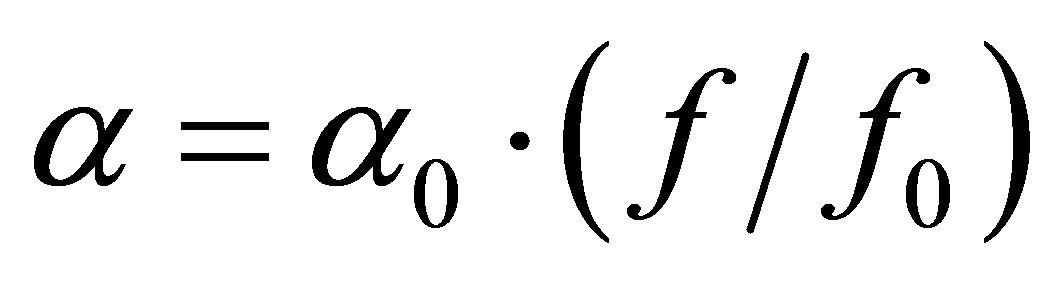 . Thus, losses are identified by successive approximations and fitted around δC = 1% in polyethylene. The reflection coefficients for the case of direct insonification AL/PE and AL/PEp are presented for N = 1, 2, 3 periods, in Figures 5(a) and (b), respectively. Lenoir. et al. [9] shown that, in the case of AL/PE configuration, the reflection coefficients reach their final spectra since N ³ 2 periods. It is also the case for the AL/PEp configuration for which the reflection spectrum is flattened. Effectively,
. Thus, losses are identified by successive approximations and fitted around δC = 1% in polyethylene. The reflection coefficients for the case of direct insonification AL/PE and AL/PEp are presented for N = 1, 2, 3 periods, in Figures 5(a) and (b), respectively. Lenoir. et al. [9] shown that, in the case of AL/PE configuration, the reflection coefficients reach their final spectra since N ³ 2 periods. It is also the case for the AL/PEp configuration for which the reflection spectrum is flattened. Effectively,
 (a)
(a) (b)
(b)
Figure 5. Reflection spectra |Rd|2 for a direct insonification, for N = 1, 2, 3 periods of (a) AL/PE and (b) AL/PEp periodic structures, respectively.
 (a)
(a) (b)
(b)
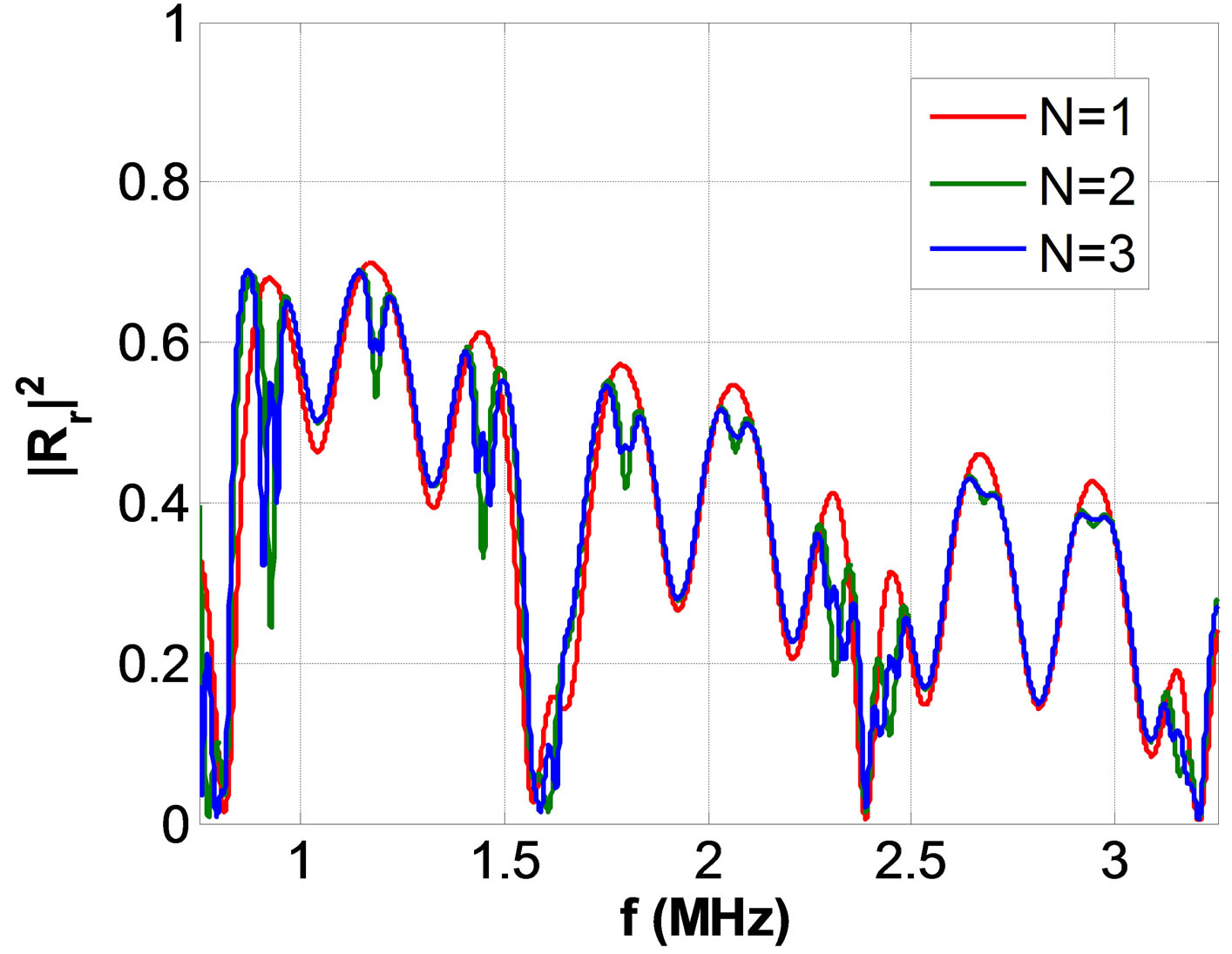
Figure 6. Reflection spectra |Rr|2 for a reverse insonification, for N = 1, 2, 3 periods of (a) PE/AL and (b) PEp/AL periodic structures, respectively.
 (a)
(a)
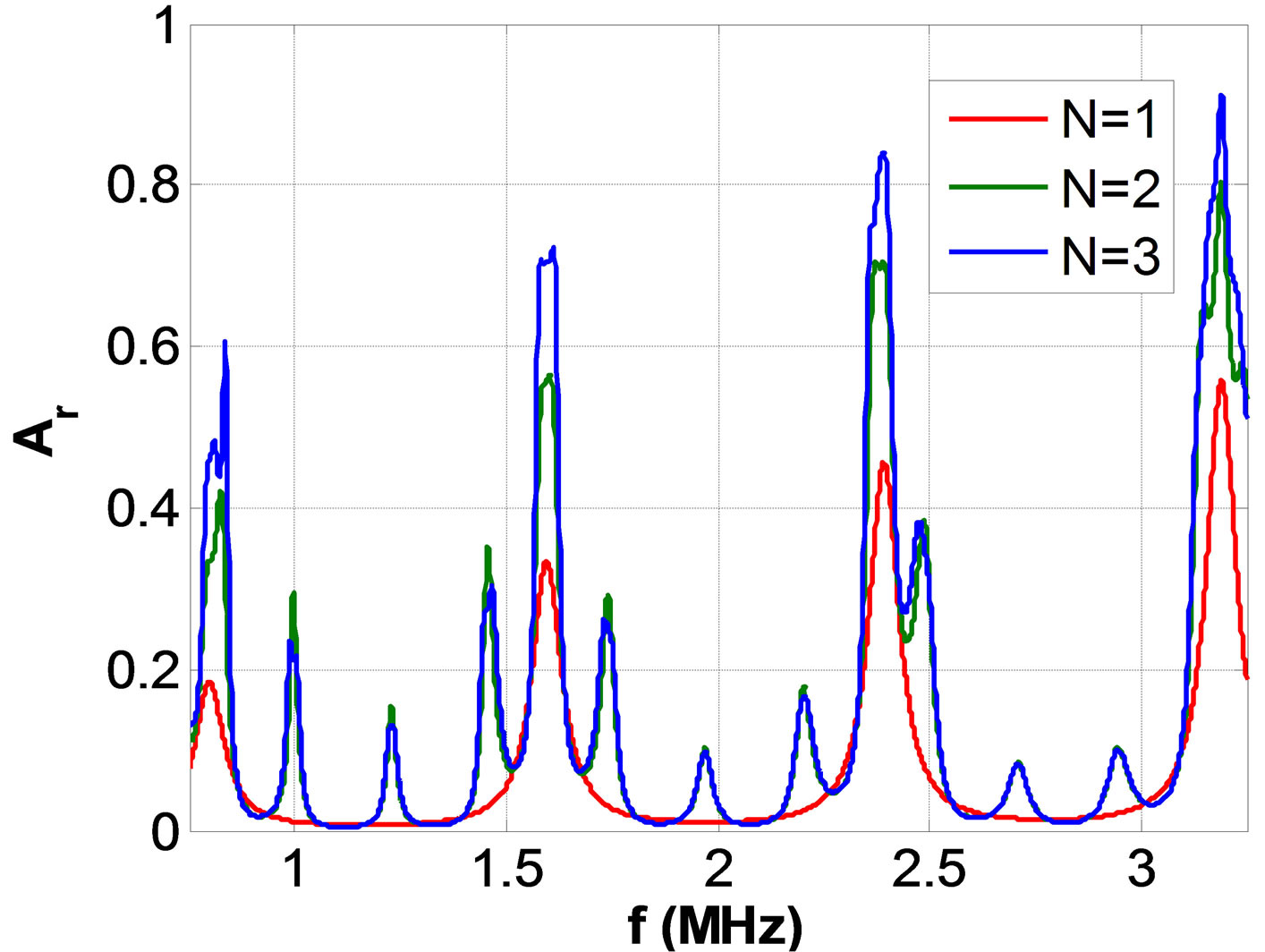
Figure 7. (a) Transmission spectra |T|2 for AL/PEp or PEp/ AL periodic structures and (b) Attenuation spectra Ar for PEp/AL periodic structures, both for N = 1, 2, 3 periods.
 (a)
(a) (b)
(b)
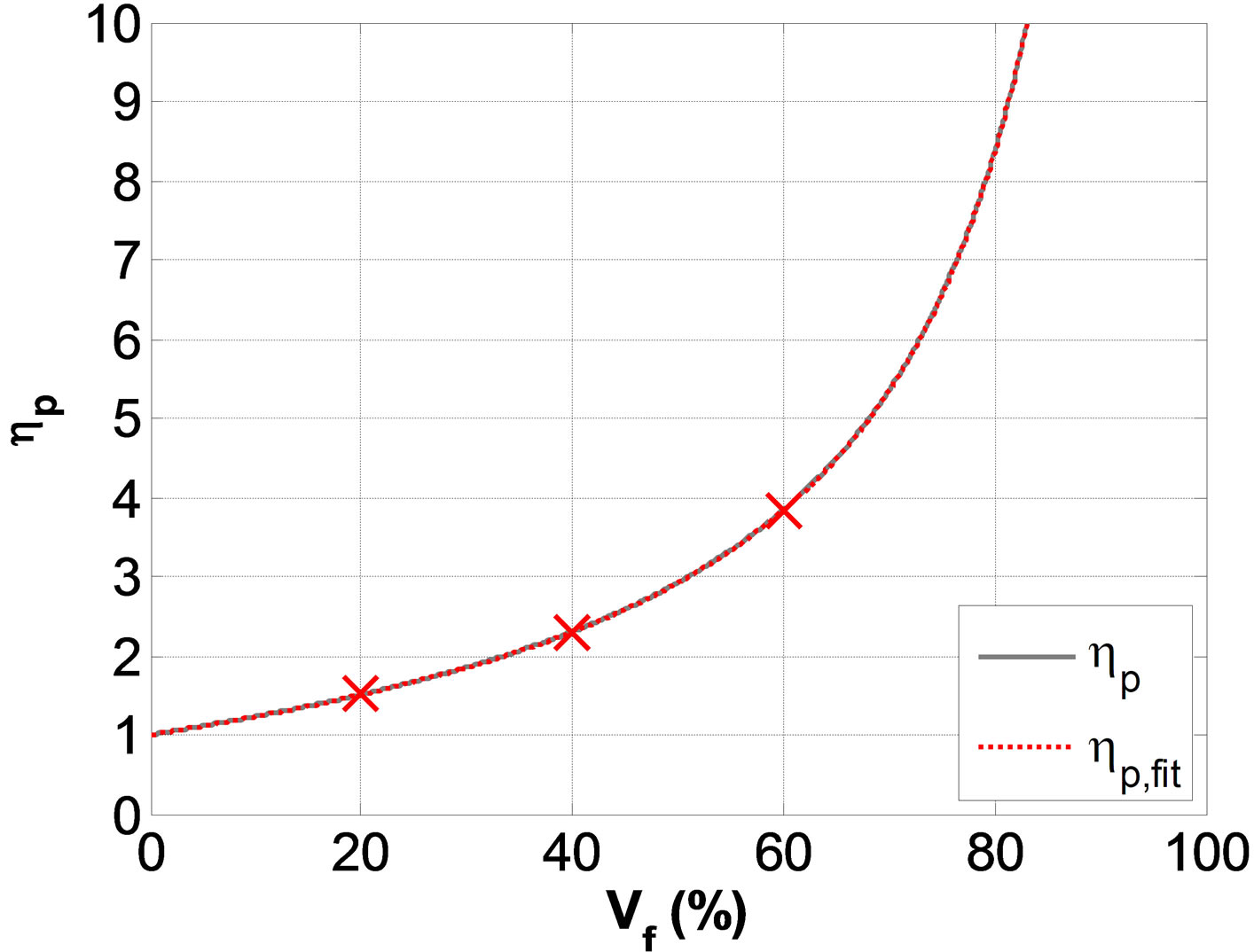
Figure 8. (a) Porosity efficiency on the acoustic impedance ratio ηp (Vf) of AL/Pep relatively to AL/PE, and resulting values for Vf = 20, 40 and 60% (red crosses) and (b) porosity ratio effect for Vf = 20, 40 and 60% on the reflection spectra |Rr|2, for N = 3 periods on PEp/AL periodic structures.
the presence of porosities in the polyethylene plates makes it behave like a slower propagation medium. Moreover, the wavelength in the porous PEp plate is smaller than the massive PE plate: lL,PEp < lL,PE. This results in an increase attenuation APEp in the PEp thickness, which is expressed here as:
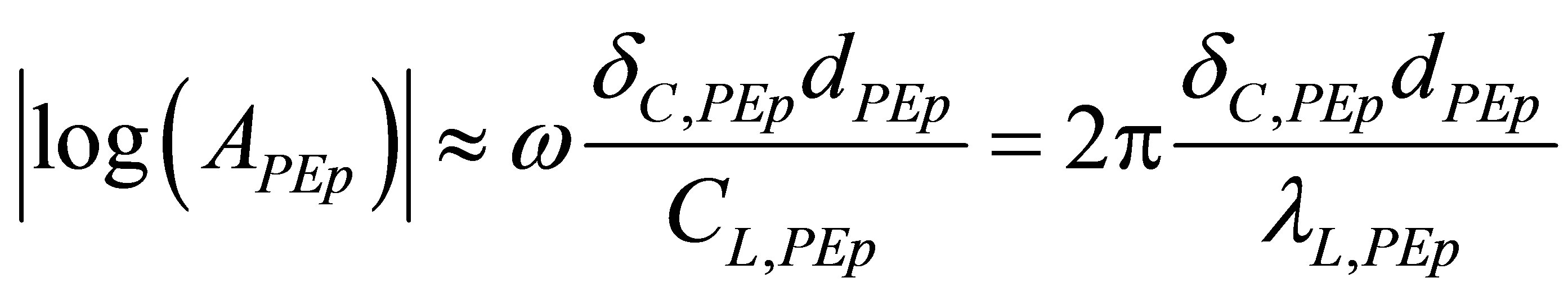 (13)
(13)
As demonstrated in Section 3, the effective velocity in the porous PEp layer decreases as a function of Vf (equations (7) and (8)). This can be summarized by: CL,PEp < CL,PE, causes APEp > APE. Moreover, due to porosities, losses in the porous PEp plate should also increase drastically: dC,PEp > dc,PE, also implying APEp > APE. Nevertheless, losses were considered strictly constant all along the study: we chose to fix dC,PEp = dC,PE = 1%. The case of reverse insonification, i.e. PE/AL and PEp/AL structures, is illustrated in Figures 6(a) and (b), respectively. In the PEp/AL configuration, the undulations practically disappear and the amplitude of the reflection coefficients strongly decreases with frequency, as does the attenuation APE or APEp (equation (13)), in the PE or PEp layers, respectively. Moreover, the minimum of the reflection coefficients tends towards zero for the case PEp/AL. Concerning the transmission coefficient, as observed on Figure 7(a), in both direct case AL/PEp or reverse case PEp/AL, the forbidden bands gaps appear since N ³ 2 periods. As a comparison, those reported by Lenoir et al. [10] on AL/PE or PE/AL configurations, who observed the forbidden bands gaps in the crystal only from N ³ 4 periods. The attenuation coefficient is also plotted in the case of reverse insonification of porous PEp based structures PEp/AL (Figure 7(b)). The amplitudes of the peaks increase according to the number of periods and frequency. The maxima are observed at the frequencies 1.6, 2.4 and 3.2 MHz, in the bandwidth of the transducer. In addition, the attenuation coefficient exhibits maxima at multiples of the frequency shift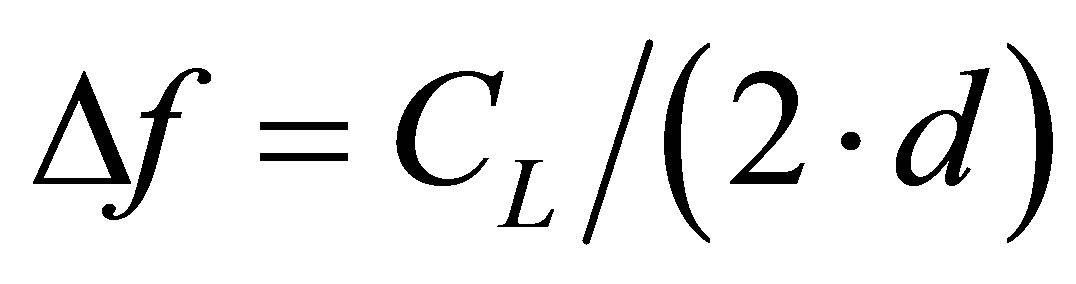 , where DfAL » 800 kHz and DfPEp » 245 kHz, for the AL and PEp plates respectively. As previously, in the case of PE/AL stacks, there were more fluctuations of the attenuation coefficient, unlike PEp/AL stacks, where fluctuations disappear faster as the number of periods N increases.
, where DfAL » 800 kHz and DfPEp » 245 kHz, for the AL and PEp plates respectively. As previously, in the case of PE/AL stacks, there were more fluctuations of the attenuation coefficient, unlike PEp/AL stacks, where fluctuations disappear faster as the number of periods N increases.
3.2. Acoustic Impedance Contrast
As mentioned in Section 1, the acoustic impedance contrast can be varied through the porosity ratio of the acoustically lighter layer. Thus, porosity efficiency hp on the acoustic impedance ratio is a figure of merit defined as
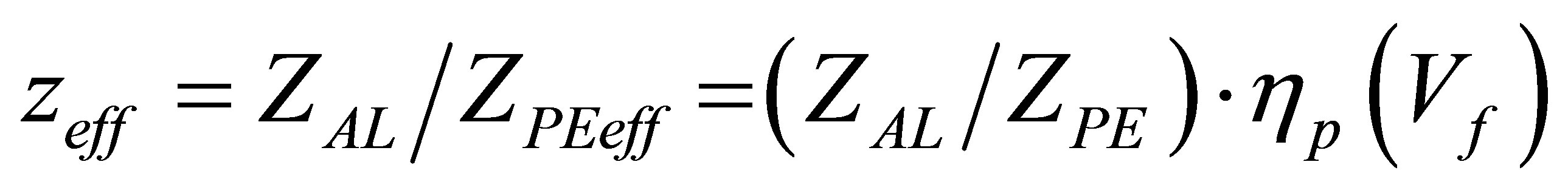 :
:
 (14)
(14)
The porosity efficiency approximated expression hp (equation (14) and Figure 8(a)) results form the HS-ort homogenization model (Equation (8)). The three volume fraction of porosity Vf = 20, 40, and 60%, corresponding to hp = 1.5, 2.3 and 3.8 respectively (Figure 8(a)) illustrates the effect of the acoustic impedance contrast (Figure 8(b)). It can be observed that the minima are periodically spaced by a frequency shift DfPEp » 245, 210 and 190 kHz, corresponding to the effective longitudinal velocities CL,PEp = 1960, 1720 and 1540 m/s associated to the porosity ratio Vf = 20, 40, and 60%, respectively. Moreover, the amplitude of the oscillations of the reflection spectra |Rr|2 due to the PEp effective properties are increased, since they are directly related to the acoustic impedance contrast.
4. Conclusion
In this study, the influence of the defects with emerging holes was investigated. The effective properties resulting from the induced porosity ratio were deduced from the HS-ort homogenization model. The reflection and transmission properties of ultrasonic waves in the multilayer periodic structure, highlighted that the emerging holes facilitate the appearance of the forbidden band gaps. Moreover, in the AL/PEp configuration, for a minimum number of periods (N = 1 or 2), the reflection coefficients do not evolve in a considerable way. Finally, with the crystal without holes, it takes at least two periods (N = 2) to reach the final shape of the reflection spectrum. With AL/PEp elementary stack, only one period (N = 1) is required to converge. It was showed theoretically that throughout holes and related effective properties at constant loss had a significant influence, not only in term of amplitude, but also in term of existence or position of minima of reflection. In the future work, we wish to investigate further experiments in order to propose a model for one-dimensional periodic structures with drilled calibrated porosity ratio drilled structures, in the perspective of ultrasoundproofing applications.
REFERENCES
- D. Maa, “Micro-Perforated-Panel Wideband Absorbers,” Noise Control Engineering Journal, Vol. 29, No. 3, 1987, pp. 77-84. doi:10.3397/1.2827694
- F.-C. Lee and W.-H. Chen, “Acoustic Transmission Analysis of Multi-Layer Absorbers,” Journal of Sound and Vibration, Vol. 248, No. 4, 2001, pp. 621-634. doi:10.1006/jsvi.2001.3825
- S. Hur, D. Lee and Y. Kwon, “A Study on the Sound Absorption Performance of Multiple Layer Perforated Plate Systems,” Proceedings of the KSME Spring Annual Conference, 2002, pp. 688-693.
- A. Nilsson and B. Rasmussen, “Sound Absorption Properties of a Perforated Plate and Membrane Construction,” Acta Acustica United with Acustica, Vol. 57, No. 3, 1985, pp. 139-148.
- X. Jing and X. Sun, “Experimental Investigations of Perforated Liners with Bias Flow,” Journal of the Acoustical Society of America, Vol. 106, No. 5, 1999, pp. 2436-2441. doi:10.1121/1.428128
- C. Zwikker and C. Kosten, “Sound Absorbing Materials,” Elsevier Pub. Co., New York, 1949.
- J. Kang and H. Fuchs, “Predicting the Absorption of Open Weave Textiles and Micro-Perforated Membranes Backed by an Air Space,” Journal of Sound and Vibration, Vol. 220, No. 5, 1999, pp. 905-920. doi:10.1006/jsvi.1998.1977
- D. Lee and Y. Kwon, “Estimation of the Absorption Performance of Multiple Layer Perforated Panel Systems by Transfer Matrix Method,” Journal of Sound and Vibration, Vol. 278, No. 4-5, 2004, pp. 847-860. doi:10.1016/j.jsv.2003.10.017
- O. Lenoir and P. Maréchal, “Study of Plane Periodic Multilayered Viscoelastic Media: Experiment and Simulation,” IEEE International Ultrasonics Symposium Proceedings, Rome, 20-23 September 2009, pp. 1028-1031. doi:10.1109/ultsym.2009.5441518
- O. Lenoir, P. Maréchal, and P. Rembert, “Study of Period and Structure Modes of Periodic Multilayers with The S Matrix Formalism,” Congrès Français de Mécanique, Marseille, 2009. http://mathserv.cnam.fr/~wilk/CFM2009/Guide_du_congressiste/sessions/DOC/975.pdf
- P. Maréchal and O. Lenoir, “Effet de Déperiodisation dans une Structure Multicouche Plane Viscoélastique: Expérience et Simulation,” In : Société Fraçaise d’Acoustique SFA, Ed., 10 ème Congrès Français d’Acoustique, Lyon, 2010.
- S. Rokhlin and L. Wang, “Stable Recursive Algorithm for Elastic Wave Propagation in Layered Anisotropic Media: Stiffness Matrix Method,” Journal of the Acoustical Society of America, Vol. 112, No. 3, 2002, pp. 822-834. doi:10.1121/1.1497365
- P. Maréchal, L. Haumesser, L. Tran-Huu-Hue, J. Holc, D. Kuscer, M. Lethiecq and G. Feuillard, “Modeling of a High Frequency Ultrasonic Transducer Using Periodic Structures,” Ultrasonics, Vol. 48, No. 2, 2008, pp. 141- 149. doi:10.1016/j.ultras.2007.11.007
- S. Ahmed and F. Jones, “A Review of Particulate Reinforcement Theories for Polymer Composites,” Journal of Materials Science, Vol. 25, No. 12, 1990, pp. 4933-4942. doi:10.1007/BF00580110
- E. Garboczi and A. Day, “An Algorithm for Computing the Effective Linear Elastic Properties of Heterogeneous Materials: Three-Dimensional Results for Composites with Equal Phase Poisson Ratios,” Vol. 43, No. 9, 1995, pp. 1349-1362.
- J. Poutet, D. Manzoni, F. Hage-Chehade, J.-F. Thovert and P. Adler, “The Effective Mechanical Properties of Random Porous Media,” Journal of the Mechanics and Physics of Solids, Vol. 44, No. 10, 1996, pp. 1587-1620. doi:10.1016/0022-5096(96)00051-8
- S. Torquato, “Effective Stiffness Tensor of Composite Media: II. Applications to Isotropic Dispersions,” Journal of the Mechanics and Physics of Solids, Vol. 46, No. 8, 1998, pp. 1411-1440. doi:10.1016/S0022-5096(97)00083-5
- K. Pithia, “An Approximate Calculation on the Elastic Constants of a Solid Containing Varying Volume Fractions of Cavities,” Physica A: Statistical Mechanics and its Applications, Vol. 222, No. , 1995, pp. 25-31.
- A. Roberts and E. Garboczi, “Elastic Properties of Model Porous Ceramics,” Journal of the American Ceramic Society, Vol. 83, No. 12, 2000, pp. 3041-3048. doi:10.1111/j.1151-2916.2000.tb01680.x
- S. Meille and E. Garboczi, “Linear Elastic Properties of 2D and 3D Models of Porous Materials Made from Elongated Objects,” Modelling and Simulation in Materials Science and Engineering, Vol. 9, No. 5, 2001, pp. 371- 390. doi:10.1088/0965-0393/9/5/303
- M. Wang and N. Pan, “Elastic Property of Multiphase Composites with Random Microstructures,” Journal of Computational Physics, Vol. 228, No. 16, 2009, pp. 5978- 5988. doi:10.1016/j.jcp.2009.05.007
- G. C. Gaunaurd and H. Uberall, “Resonance Theory of the Effective Properties of Perforated Solids,” Journal of the Acoustical Society of America, Vol. 71, No. 2, 1982, pp. 282-295. doi:10.1121/1.387452
- G. Gaunaurd, E. Callen and J. Barlow, “Pressure Effects on the Dynamic Effective Properties of Resonating Perforated Elastomers,” Journal of the Acoustical Society of America, Vol. 76, No. 1, 1984, pp. 173-177. doi:10.1121/1.391090
- Z. Hashin and S. Shtrikman, “A Variational Approach to the Theory of the Elastic Behaviour of Multiphase Materials,” Journal of the Mechanics and Physics of Solids, Vol. 11, No. 2, 1963, pp. 127-140. doi:10.1016/0022-5096(63)90060-7
- Z. Hashin, “On Elastic Behaviour of Fibre Reinforced Materials of Arbitrary Transverse Phase Geometry,” Journal of the Mechanics and Physics of Solids, Vol. 13, No. 3, 1965, pp. 119-134. doi:10.1016/0022-5096(65)90015-3
- Z. Hashin, “Analysis of Composite Materials—A Survey,” Journal of Applied Mechanics, Vol. 50, No. 3, 1983, pp. 481-505. doi:10.1115/1.3167081
- C. H. Arns, M. A. Knackstedt, W. V. Pinczewski and E. J. Garboczi, “Computation of Linear Elastic Properties from Microtomographic Images: Methodology and Agreement between Theory and Experiment,” Geophysics, Vol. 67, No. 5, 2002, pp. 1396-1405. doi:10.1190/1.1512785
- C. Hsieh, W. Tuan and T. Wu, “Elastic Behaviour of a Model Two-Phase Material,” Journal of the European Ceramic Society, Vol. 24, No. 15-16, 2004, pp. 3789-3793. doi:10.1016/j.jeurceramsoc.2004.02.002
- C. Hsieh and W. Tuan, “Elastic Properties of CeramicMetal Particulate Composites,” Materials Science and Engineering: A, Vol. 393, No. , 2005, pp. 133-139. doi:10.1016/j.msea.2004.10.009
- H. Hu, L. Onyebueke and A. Abatan, “Characterizing and Modeling Mechanical Properties of Nanocomposites— Review and Evaluation,” Journal of Minerals & Materials Characterization & Engineering, Vol. 9, No. 4, 2010, pp. 275-319.
- H. Franklin, E. Danila and J. Conoir, “S-Matrix Theory Applied to Acoustic Scattering by Asymmetrically FluidLoaded Elastic Isotropic Plates,” Journal of the Acoustical Society of America, Vol. 110, No. 1, 2001, pp. 243- 253. doi:10.1121/1.1373636
NOTES
*Corresponding author.

