ABSTRACT

The paper presents an analytical method of identifying the curvature of the turnout diverging track consisting of sections of varying curvature. Both linear and nonlinear (polynomial) curvatures of the turnout diverging track are identified and evaluated in the paper. The presented method is a universal one; it enables to assume curvature values at the beginning and end point of the geometrical layout of the turnout. The results of dynamics analysis show that widely used in railway practice, clothoid sections with nonzero curvatures at the beginning and end points of the turnout lead to increased dynamic interactions in the track-vehicle system. The turnout with nonlinear curvature reaching zero values at the extreme points of the geometrical layout is indicated in the paper as the most favourable, taking into account dynamic interactions occurring in the track-vehicle system.

Keywords:

Railway Turnouts, Curvature Modelling, Dynamics Analysis

1. Introduction

Typical, used since the beginning of railway engineering, geometrical layout of the turnout diverging track consists of a single circular arc without transition curves. It introduces sudden, abrupt changes of the horizontal curvature of the layout at the beginning and end of the turnout diverging track, which increases dynamic interactions in the track-vehicle system, particularly unfavourable in high speed rail (HSR). Investigation and evaluation of geometrical layouts of the turnout diverging track are still a current issue.

Recently, aiming at smoothing changes of the curvature at the neuralgic regions of the turnout diverging track, the clothoid sections have been introduced at both sides of the circular arc [1] [2] [3] . The curvature of the applied clothoid sections in many cases does not reach zero value at the extreme points (i.e. at the beginning and end points of the turnout). The paper presents the evaluation of the selected geometrical layouts of the turnout diverging track to indicate the most favourable solution for HSR.

In the turnout with linear curvature sections, a diverging track is divided into three zones (Figure 1):

・ a beginning zone of the length, in which curvature increases linearly from

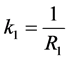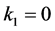(or) to,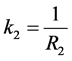

・ a middle zone of the length 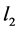with constant curvature,

・ an end zone of the length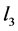, in which curvature decreases linearly from

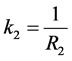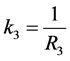, to (or).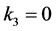

The various values of curvature and length of each section can be applied in the designing process. Curvature of the turnout diverging track is described by an analytical function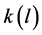, where 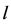stands for the length of the curve.

This paper presents the identification of analytical functions 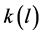for linear curvature sections (i.e. clothoid sections) as well as for nonlinear curvature sections in the polynomial form. The identified curvatures have been compared using the dynamic model, described in [4] , to find out the most favorable solution from the point of view of minimizing the dynamic effects.

In this paper, the Cartesian coordinates of the turnout diverging tracks are not presented. The method of the identification of the Cartesian coordinates from the curvature 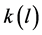is described in [4] . The determination of parametric equations and requires the expansion of the integrands into Taylor series [5] using Maxima package [6] .

2. Application of the Linear Curvature Sections

2.1. Solution for the Beginning Zone

In the beginning zone of the turnout the considered issue is identified by boundary

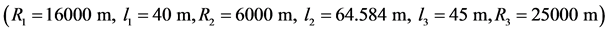conditions [2]

(1)

and a differential equation

. (2)

After determining the constants, the solution of the differential problem (1), (2) is as follows:

. (3)

The slope of the tangent at the end of the zone, for, is defined by the formula:

. (4)

2.2. Solution for the Middle Zone

In the circular arc zone, i.e. for, curvature is constant:

. (5)

At the end of circular arc the slope of the tangent is defined by the formula:

. (6)

2.3. Solution for the End Zone

In the end zone of the turnout the following boundary conditions are adopted:

(7)

for the differential Equation (2). After determining the constants, the solution of the differential problem (2), (7) is as follows:

. (8)

The slope of the tangent at the end of the turnout is defined by the formula:

, (9)

from which the turnout angle can be obtained as

. (10)

3. Application of the Nonlinear Curvature Sections

The curvature of the turnout diverging track in Figure 1 is not undoubtedly an ideal solution. The adoption of more gentle changes of the curvature at both sides of the circular arc and the assumption of zero curvature value at the extreme points (i.e. the turnout beginning and end points) of the geometric layout are worth considering.

3.1. Solution for the Beginning Zone

The following boundary conditions have been adopted:

(11)

to the differential equation

(12)

with assumption, that coefficient.

As a result of solving the differential problem (11), (12) the following curvature has been obtained:

. (13)

Function describing the curvature in the considered zone should be monotonic and should increase for. In order to obtain a feasible solution the coefficient C should be properly adjusted. It has been shown, that the appropriate. Taking into account the length of the parametric curve (13) and a curve of linear curvature (i.e. generalized clothoid) the most favourable assumption seems to be C = 1.5. Curvature in this case is as follows:

. (14)

At the end of the zone, for, the slope of the tangent is described by the formula:

. (15)

3.2. Solution for the Middle Zone

Similarly to the middle zone described in the section 2.2, i.e. for, the curvature is constant. The slope of the tangent at the end of the circular arc, for, is described by the formula:

. (16)

3.3. Solution for the End Zone

Assuming the boundary conditions:

(17)

for the differential Equation (12) the following solution has been obtained:

(18)

where

Assuming C = 1.5 the following coefficient formulas have been obtained:

The slope of the tangent at the end of the turnout, for, is defined by the formula:

. (19)

In Figure 2 the curvature of the turnout diverging track (for C = 1.5) with nonlinear curvature sections has been shown. The geometric parameters of the turnouts presented in Figure 1 and Figure 2 are conform.

4. Selection of the Geometrical Layouts of Turnout Diverging Tracks

In order to ensure a reliable comparative analysis of the geometrical layouts presented in Table 1, the following common assumptions have been adopted:

・ the turnout angle 1:n , where n = 50,

・ the curvature values, and are common to all turnouts,

・ the circular arc radius,

・ the length of the beginning zone and the end zone are similar and ensures the fulfillment of the kinematic conditions,

・ the length of the circular arc ensures reaching the assumed value of the turnout angle.

The highest velocity on a circular arc without superelevation (i.e. in the middle zone) results from the following condition:

,

while in the extreme zones the condition is as follows

where:

V―train velocity [km/h],

R―circular arc radius [m],

―acceleration on circular arc [m/s²],

―permissible value of acceleration on circular arc [m/s²],

―function describing lateral acceleration in the zones of changing curvature,

―rate of acceleration changes in the zone of changing curvature [m/s³].

―permissible value of parameter [m/s³].

It is assumed that and.

On a circular arc without transition curves (turnout 1) the acceleration changes linearly from 0 to along the length of the rigid base of wagon. Taking into account

for

with condition

the limit of the velocity is obtained as follows

. (20)

On a circular arc in the middle zone with sections of changing curvature in the beginning and end zones the limit of the velocity is described by the formula

(21)

In the beginning zone where curvature changes linearly a rate of acceleration changes is constant. In this zone the following condition should be fulfilled:

,

from which the minimal length of the beginning zone can be determined:

. (22)

Nonlinear curvature (polynomial) induces changing rate of acceleration changes along the length of the turnout. The following condition should be fulfilled:

An increase by 50% of the limit value is justified by the fact, that the value occurs only once (for l = 0), and next decreases, reaches at the end of the section (for) zero value. The condition (22) can be applied also for the end zone of the turnout.

For the assumed turnout angle 1:50 (i.e. n = 50) the following slope of the tangent has been obtained, using Equation (10):

Assuming for the turnout diverging track 1 (Table 1), using Equation (20) the maximal velocity. The length of the circular arc is obtained as follows:. The velocity limit in turnouts 2 ÷ 7 results from the Equation (21): (in the comparative analysis of the turnouts, presented in section 6, it was assumed).

The geometrical parameters of the selected seven turnouts are presented in Table 1. The lengths of the sections and result from condition (22), while the length results from the assumed slope of the tangent in the Equation (9) for linear curvature:

(23)

and in the Equation (19) for nonlinear curvature:

. (24)

The function of lateral acceleration along the layout, as proved in [4] , results directly from the layout curvature. The assumed functions of lateral acceleration for selected turnouts are presented in Table 2.

5. The Dynamic Model

With increased speed requirements on railways, the dynamic effects minimization is a current issue, especially in HSR. Basing on the assumption that horizontal curvature changes are a forcing factor of the lateral oscillations, selected seven geometrical layouts of the turnout diverging track are compared in terms on their impact on the dynamic interactions occurring in a rail-vehicle system. In the presented comparative analysis of the layouts, structural aspects of the rail

vehicle are omitted.

A dynamic model with one degree of freedom, consisting of a mass with a spring and a damper is applied to compare the dynamic interactions occurring on the various turnout diverging tracks. An additional parameter―a length of the rigid base of a wagon has been introduced, which results in referring to the lateral acceleration of the wagon mass center (arithmetic mean of accelerations occurring in the front and rear bogies).

The lateral acceleration occurring along the turnout diverging track can be described by the separate functions dedicate for different turnout zones. Assuming constant velocity along the turnout, as it is done in this paper, function for each turnout zone is presented in Table 2. Considered case includes driven horizontal harmonic oscillations X [7] described by the equation

(25)

where:

D―Lehr’s damping coefficient,

―free oscillation frequency,

.

Lehr’s damping coefficient D is used as a damping measure in the railway engineering. In the presented paper D = 0.175 and ω = 3.5 π/s are assumed. The assumed value of D has been obtained in the experimental research presented in [8] . As proved in [9] this assumption has no impact on conclusions from the comparative analysis of dynamic properties of railway geometrical layouts.

The function of oscillations, describing lateral displacement of the vehicle under the force, is the solution to the differential Equation (25). The function is the resultant of the static component and the system oscillations. From the point of view of dynamic effects evaluation the resultant acceleration of oscillation motion is essential. The maximum amplitude of the acceleration of oscillating motion and indicator defined as follows

(26)

where:

―the point at which curvature of the turnout diverging track changes,

―the length of the section on which oscillations are damped,

are assumed as criteria of the dynamic effects evaluation presented in Section 6.

6. Results of the Dynamics Analysis

The length of the rigid base (it has been assumed) used in the dynamic model results in more gentle changes of lateral acceleration, It is presented in Figure 3 and Figure 4 as the linea_corr for turnout 1 and 2 (Table

1).

The acceleration of oscillating motion, computed numerically using the dynamic model described in section 5, for the selected seven geometrical layouts of turnout diverging track (Table 2 and Table 3) is presented in Figures 5-12.

Apart from the beginning and end zones of the turnout diverging track, the dynamic interactions occur also at the beginning and end of the middle zone, as shown in Figure 7.

The comparative analysis of the selected layouts of the turnouts diverging track has been carried out using dynamic indicators: (26) and, based on acceleration of oscillating motion from Figures 5-12. The computed values of and for the selected seven turnouts are presented in Table 3.

As shown evidently in Table 3 and Figures 5-12 the greatest values of acceleration in oscillating motion occur in the beginning and the end zone of the turnout diverging track, wherein the value of the acceleration is influenced by the assumed curvatures and. In geometrical layouts of the turnout diverging track, in which or (turnout 2 and 5 in Figure 2, Figure 3 and Figure 10), the dynamic interactions are significantly greater (approximately 100 times greater) than in the layouts in which and (turnout 4 and 7 in Figure 9 and Figure 12).

The assumption of (turnout 3―Figure 8 and turnout 6―Figure 11) results in a radical reduction of the acceleration in oscillating motion in the end zone of the turnout diverging track. The simultaneous adoption of both conditions: and leads to a reduction of the dynamic interactions

along the whole turnout diverging track; it is concerned layouts with sections of linear curvature (turnout 4―Figure 9) as well as layouts with sections of nonlinear curvature (turnout 7―Figure 12).

The presented results leads to conclusion that widely applied in a railway practice “clothoid sections” with curvatures at the beginning and end points of the turnout diverging track are not justified. The dynamic properties of the layout can be significantly improved by assuming and at the mentioned points, accepting the fact that the length of the resulting turnout will

slightly increase (Table 1).

The acceleration in oscillating motion occurring at the beginning and at the end of the middle zone is not dependent on the curvatures values and, adopted in the beginning and the end zone of the turnout, but depends on the curvature characteristics. Linear curvatures and (turnouts 2 ÷ 4, Figures 6-9) induce greater values of dynamic indicators (Table 3) than nonlinear ones (turnouts 5 ÷ 7, Figures 10-12).

Taking into account the dynamic properties and the length of the layout, the turnout diverging track 7 is definitely the most favourable. Turnout 7 in comparison with turnout 4 has better dynamic properties in the middle zone, shorter length and insignificantly worse values of dynamic indicators in the beginning and end zones (Table 3).

7. The Most Favourable Geometrical Layout of the Turnout Diverging Track

As a result of dynamics analysis it has been proved that the most favourable dynamic properties can be achieved by applying a nonlinear curvature in the beginning and end zones of the turnout diverging track and assuming zero curvature value at the extreme points of the geometrical layout.

Assuming and the curvature of the turnout is defined as follows:

・ in the beginning zone, for, based on the Equation (14) the following formula is obtained

(27)

・ in the middle zone, i.e. for, the curvature is constant

・ in the end zone, for the curvature is described by the Equation (18) with the following coefficient values:

The slope of the tangent at the end of the turnout, for, is as follows

. (28)

In Figure 13 the curvature of the most favorable turnout diverging track 7 is presented.

8. Conclusions

Typical turnout diverging track consists of a single circular arc without transition curves. It introduces sudden, abrupt changes of the horizontal curvature of the layout at the beginning and end of the turnout diverging track, which increases dynamic interactions in the track-vehicle system, particularly unfavourable in HSR.

The paper presents a universal, analytical method of identifying the curvature of the turnout diverging track. Both linear and nonlinear (polynomial) curvatures of the turnout diverging track are identified and evaluated using a dynamic

model. The presented method enables to assume the curvature values at the beginning and end point of the geometrical layout of the turnout. The length of the circular arc is adjusted to obtain the assumed turnout angle.

Recently, aiming at smoothing changes of the curvature at the neuralgic regions of the turnout diverging track, the clothoid sections have been introduced at both sides of the circular arc. The curvature of the applied clothoid sections changes linearly but in many cases does not reach zero value at the extreme points (i.e. at the beginning and end points of the turnout). The results of dynamics analysis presented in the paper show that clothoid sections with nonzero curvature at the beginning and end points of the turnout lead to increased dynamic interactions in the track-vehicle system. Dynamic interactions can be decreased by applying curvature reaching zero at the extreme points of the turnout.

The paper presents the evaluation of the selected seven geometrical layouts of the turnout diverging track and indicates the most favourable solution for HSR. The most favourable from the dynamic properties point of view is the turnout diverging track with nonlinear curvature reaching zero values at the extreme points of the turnout.

Cite this paper

Koc, W. and Palikowska, K. (2017) Dynamic Analysis of the Turnout Diverging Track for HSR with Variable Curvature Sections. World Journal of Engineering and Technology, 5, 42-57. https://doi.org/10.4236/wjet.2017.51005

References