World Journal of Engineering and Technology
Vol.02 No.03(2014), Article ID:48695,9 pages
10.4236/wjet.2014.23022
CAE Characterization and Optimization of Automotive Seat Rattle Noise
Milad Tatari1, Mohammad Fard2*, Naser Nasrollahzadeh1, Mohammad Mahjoob1
1Department of Mechanical Engineering, School of Engineering, University of Tehran, Tehran, Iran
2School of Aerospace, Mechanical and Manufacturing Engineering, RMIT University, Melbourne, Australia
Email: m.tatari@ut.ac.ir, *mohammad.fard@rmit.edu.au, n.nasrolahzadeh@ut.ac.ir, mmahjoob@ut.ac.ir
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 May 2014; revised 15 July 2014; accepted 30 July 2014
ABSTRACT
The vehicle seat rattles or, in general, BSR (buzz, squeak, and rattle) noises are one of the major issues, which are directly linked to the NVH (noise, vibration and harshness) quality of the vehicle. Predicting and improving the seat BSR noise in early design phase is still challenging. This is mainly due to the complexity, nonlinearity and uncertainty of the impact mechanism at joints contributed to the rattle. Here, it is shown that there is a strong link between the seat structural dynamics and the seat rattle noise so that the seat rattle noise can be predicted and controlled from the seat structural analysis in early design phase. Accordingly, two experiments are designed for this study. The first experiment is set up to characterize the seat resonant frequencies and its corresponding structural mode-shapes. The second experiment is designed to measure the seat- radiated noise when it goes under vibration excitation. Alternatively, a concept CAE (Computer Aided Engineering) model of the seat is developed and the seat structural dynamics is character- ized by using this analytical model. The model is developed to allow designing the seat-structure modifications as well as examining the effects of the modifications on the rattle noise. Compari- sons of the results of the simulation and experiment validate the developed CAE model. The re- sults confirm that by changing the seat resonant frequency, the rattle noise and in general BSR noise can be improved or controlled accordingly. Consequently, for the seat system which has an identifiable structural dynamics, the BSR noise can be managed and controlled in early design phase by using the seat CAE model.
Keywords:
Rattle Noise, Structural Dynamics, Resonant Frequency, Mode Shape, Modal Analysis, CAE Concept Model

1. Introduction
The vehicle seat is one of the major components that have potential to be a source of annoying BSR (buzz, squeak, and rattle) noise [1] . Controlling BSR is becoming essential with the trend toward using lightweight materials combined with the increase in number of the seat sub-components such as electronic gadgets [2] . Moreover, in the quiet cabin of the modern vehicles, BSR has become more prominent as customers perceive BSR as direct indicators of vehicle build quality and durability [3] . According to a market survey, squeaks and rattles are the third most important customer concern in cars after three months of ownership [3] . Furthermore, upcoming electric cars will highlight the importance of the BSR issues [4] . BSR is generally caused by loose or overly flexible elements under excitation. BSR is originated from frictional movement between two parts or from the impact between two parts. The rattle noise is caused when surfaces close to each other move perpendicular to each other due to insufficient attachments or insufficient structural strength [4] . In general, the main causes of the BSR are structural deficiencies, incompatible material pairs, and poor geometrical design [4] [5] .
Modern advances in the vehicle noise and vibration control engineering have reduced the transmission of the vibration or noise from different sources such as powertrain or road into the passenger cabin [1] [6] . This is mainly due to the development and innovations in virtual or analytical techniques for the structure-borne or airborne noise control in early design phase [7] [8] . Despite the importance of the BSR noises, many of them are detected after production phase of the components, or some even after the vehicle is launched. Therefore, predicting and controlling BSR in the early design phase is important to be investigated [9] [10] . In other words, a possible analytical design method minimizes find-and-fix physical tests and provides an upfront solution for the BSR noise. Nevertheless, development of a robust analytical method for improving the BSR in the vehicle components has always been challenging. This is mainly due to the complexity, nonlinearity, and uncertainty of the dynamics of the impact or sliding mechanisms at joints contributed to the BSR. Some vehicle components such as door trims exhibit a wide range of critical frequencies with no proper global mode shapes and their BSR may happen in a wide excitation frequency band [11] . Nevertheless, the vehicle seat structure has a robust structural dynamics, which generally exhibits a maximum three known vibration mode shapes at low frequencies [12] [13] (<80 Hz). Furthermore, in modern vehicles, the seat is exposed to the low level of the floor or seat mountings vibrations, which unlikely causes the seat sub-components BSR at frequencies away from the seat resonances.
This paper shows that the seat rattle noise can be predicted and controlled in early design phase by characterizing and controlling the seat structural dynamics. Experiments are designed to first characterize the seat resonant frequencies/mode-shapes and second to measure the seat rattle noise. It is shown that the rattles of the seat components can be predicted and managed by modifying the seat structural dynamics. Such upfront knowledge about the seat rattle can greatly assist to provide robust solutions for preventing or controlling the seat rattle in early design phase [4] . The structural dynamics of the seat is also characterized by using the developed CAE (Computer Aided Engineering) model of the seat [12] [14] - [16] . The concept modelling method is used for the CAE modelling of the seat structure [14] [16] . The model is developed to allow us to probe the effects of seat- structure modifications on the rattle noise. Comparisons of the results of the simulation and experiment validate the developed CAE model. The experiment and simulation results show that the seat has two structural resonances in low frequency range (<50 Hz); one at around 31 Hz, which is the seat torsion and the other at around 48 Hz, which is the seat fore-aft bending. The noise measurement result reveals that the seat generates high level of the rattle noise when the seat excitation vibration is close to the seat structure torsion resonance (31 Hz). We have further confirmed that the occurrence of the rattle is related to the seat structural dynamics and it can be controlled and managed by modifying the structure. Two modifications are designed by using the seat CAE model. One modification is designed for increasing the seat torsion resonance nearly 4 Hz, and a second modification is done for decreasing the seat torsion resonance nearly 4 Hz. The designed modifications are then applied on the test seat and the rattle noise is measured on the two modified seats. The results show no more high level of the rattle noise for the two modified seats. These confirm that by changing the seat resonant frequency, the rattle noise and in general BSR noise can be changed accordingly. Consequently, for the seat system, which has an identifiable structural dynamics, the BSR noise can be managed and controlled in early design phase by using the seat CAE model. Furthermore, such early phase modifications of the seat structure are more robust than merely tuning the joints associated with BSR. In fact, the proposed modifications of the structure control the seat resonances and therefore transfer less vibration into the sub-components, which are vulnerable to rattle.
2. Method
2.1. Seat Modeling
A selected vehicle seat (a mid-size sedan car) is modelled by using FE methods and CAE techniques. The model of the seat must be correlated with its corresponding test data and it will be used instead of the seat. In other words, the model is developed to characterize the major seat structural dynamic behaviours such as resonant frequencies and corresponding mode shapes. Hence, a concept model, which characterizes the main attributes of the system, is developed for the seat. It is worthwhile to mention that due to the need of the industry for the fast and high performance computations, the CAE concept modeling method of the automotive body is still an attractive research area for the automotive CAE investigators [17] . According to the CAE concept modeling, the FE model of the seat structure is created via concept beams and joints. The detailed method of CAE modeling or concept modeling is extensively discussed in the literature [12] - [15] . Altair Hyper Works and MSC Nastran software are used for modeling and processing of the seat. The seat frame is made from steel and the steel properties have been used for the structure of the CAE model.
Main members of the seat are modelled using beam elements (e.g., PBEAM in Nastran software) such that their cross sections have exactly been the same as the corresponding sections at the seat. Therefore, all calculated properties of the beam elements such as bending and torsional moments of inertia are as close as possible to the physical model of the seat structure. For example, the seat members such as backrest, side members are simplified using beam modeling approximation.
In CAE concept modelling method, creation of a simple and reliable model for the joints is very important. Extensive researches are reported in the literature about the concept modelling of the main joints in the structure [15] . In this research, Guyan method [18] is used to create simple and reliable concept joints. Guyan Reduction is a method to condense the FE model of structures into a reduced description in terms of the stiffness and mass matrices at the end nodes where the joints connect to the corresponding members. Neglecting the inertia effects in calculating reduced model, Guyan method is also called static condensation. Equation (1) is the general form of the static finite element model.
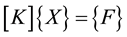 (1)
(1)
where K is the stiffness matrix, F and X are the force and the displacement vectors, respectively. By identifying boundary degrees of freedom (index b), which must be retained in the solution, and internal degrees of freedom (index i), which are to be removed by static condensation, the system of Equation (1) can be partitioned as follows:
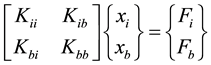 (2)
(2)
By substitution of 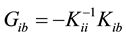 into the first row of Equation (2), the Equation (3) is derived:
into the first row of Equation (2), the Equation (3) is derived:
 (3)
(3)
Finally static condensation matrix is obtained as:
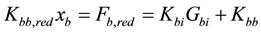 (4)
(4)
The details about Guyan method can be found in the literature [18] .
In addition, it is important to note that static condensation gives exact stiffness matrix, while it is just an approximation for the mass matrix. Therefore when this method is exploited it is assumed that inertia forces on internal DOFs are less important than elastic forces transmitted by the boundary DOFs.
After modelling the seat structure; cushion mass effects are added to the structure using non-structural mass. In other words, the foam cushions are not modelled in detailed as their stiffness contribution to the seat structure are negligible in low frequencies (<80 Hz). The total mass of the seat cushion, in the selected vehicle seat, is 6.0 kg.
2.2. Experimental Method
2.2.1. Modal Testing
Experimental modal analysis is utilized to characterize the seat structural resonant frequencies and its corresponding mode shapes. Impact hammer test, which is a common method in modal testing, was used to extract the seat structural resonances and mode shapes. The modal test setup consisted of a hammer (Rion PH-51), charge amplifier (B & K 2786), three axial accelerometers, data logger (B & K 356˚C) and Pulse 12 software. The seat structure was suspended from bungee cords (elastic ropes) to allow the seat system to be nearly free in six axes. Therefore, the seat modal characteristics were measured in the free-free boundary condition. The mounting of the accelerometers to the different parts of the seat frame was done using adhesive wax [12] . To obtain proper mode shapes, thirteen points of the seat frame were measured.
2.2.2. Noise Measurement
In order to measure the BSR noise, the seat is excited by single sine inputs with frequencies between 10 Hz to 60 Hz. Note that we have applied sweep sine inputs to the seat to tune the test frequencies. The generated noise is measured at four points near right and left sides of the seat. The noise measurement system consisted of B & K microphone (B & K 2669), electromagnetic shaker (B & K 4808), amplifier (B & K 2719), data logger (B & K 356˚C) and Pulse 12 software. During the experiment, background noise was retained below 36 dB (A) at the running condition of the vibration shaker. The temperature and humidity were kept at 22.5˚C and 35% respectively. The test setup for noise measurement points at four selected points are illustrated in Figure 1.
3. Results
3.1. Simulation and Experimental Results
As already mentioned, to identify the seat rattle noise mechanism and its relation with the seat structure, it is required to characterize the seat structural dynamics. In addition to the experiment the model-based simulation results are also required for tuning and controlling the seat rattle noise. The seat structure exhibited two major torsion and for-aft bending structural modes in low vibration frequencies (<50 Hz) where the structure has more potential to be rattled. The two obtained mode shapes are illustrated in the Figure 2. As it is shown in Figure 2, the results of the experiments and corresponding model-based simulation are consistent, so that both have exhibited two torsion and for-aft shapes. Note that the experimental mode shapes are obtained from the thirteen tri-axial accelerometers.
Following the comparison of the experiment and simulation results, the values of the resonant frequencies and the values of MAC (modal Assurance Criteria) [19] have been compared (Table 1) between the experiment and the simulation. Taking above-mentioned materials into consideration, the natural frequencies error percent (∆%) and MAC of the concept and advanced models are computed to validate the developed NVH concept model. The MAC index between similar modes of two models is calculated by Equation (5), in which  and
and 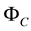 are the Matrix of Eigen vectors for the experimental results and concept model, respectively, and superscript T denotes the transpose of a vector and k shows mode number. The Eigen vectors are constructed by using main structure nodes in the test and corresponding nodes in the concept model (total thirteen nodes).
are the Matrix of Eigen vectors for the experimental results and concept model, respectively, and superscript T denotes the transpose of a vector and k shows mode number. The Eigen vectors are constructed by using main structure nodes in the test and corresponding nodes in the concept model (total thirteen nodes).
Figure 1. Test setup and four selected points for measuring the sound pressure level.
Figure 2. Seat structural dynamics: torsion modes (top) and bending modes (bottom) from simulation (left) and experiment (right) are similar.
Table 1. Comparison of the seat resonant frequencies and corresponding mode shapes between the experiment and simulation.
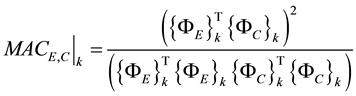 (5)
(5)
A MAC value equal to unity indicates a 100% similarity between the vibration mode shape obtained from the simulation and that of obtained from the experiment. The MAC values, in the Table 1, for the two seat torsion and fore-aft bending modes are found to be above 0.9 (Table 1), which indicates a good consistency between the modes of the developed model and the test data. Comparison of the values of torsion and fore-aft bending resonant frequencies indicate very low discrepancies (∆ < 3%).
To further validate the develop model, the inertance frequency Response Functions (FRF) are compared, between the test data and corresponding simulation data, when the seat is excited at one specified point on its frame Figure 3. Note that, here, the inertance FRF indicates the FRF that its output is measured at input point or its input and output points are same. The input and output are both measured at point “X” that is shown in Figure 3. The similarity between the FRF graphs from the test and simulation (Figure 3) further validates the developed model.
3.2. Noise Source Identification
The radiated sound pressure levels (SPL) are measured when the seat is under the excitation, at four points, which has already been numbered 1 to 4 in Figure 1. The results show that when the excitation frequency ap-

Figure 3. Comparison of the inertance FRF at point “X” between the simulation and experiment (b). The measurement point “X” is also illustrated (a).
proaches to the seat torsion resonant frequency (31 Hz), the sub-components of the seat near the seat belt buckle starts rattling. Accordingly, comparison of the SPLs measured by four microphones indicates that the microphone #3, shown in Figure 1, received higher SPL than other three microphones. Figure 4 compares the SPLs obtained from the four microphones when the seat is excited by a single sine input with 31 Hz frequency (equal to the seat torsion resonance). As it is observed, the rattle causes higher noise level (here 70 dB SPL) mainly at frequencies below 2500 Hz. Note that even the seat is excited by a single sine vibration, the rattle noise can be occurred in a wide frequency range. Furthermore, the rattle noise is also functions of additional physical properties such as the contact surface and materials of the rattling parts [3] .
By decreasing or increasing the excitation frequency from 31 Hz to 25 Hz or 35 Hz, the rattle noise is also considerably decreased (Figure 5). In other words, a wide band rattle noise is seen when the seat is excited at its resonance frequency. This confirms that the occurrence of the seat sub-components rattle is linked to the seat resonant frequency, so that by changing the excitation frequency away from the seat structural resonance, the rattle noise can be managed.
3.3. The Effects of the Seat Structure Optimization on the Rattle Noise
As it was seen, seat structural dynamic characteristics have large contributions to the seat rattle noise generation. The rattle noise can be predicted and controlled in early design phase by analyzing and modifying the seat structure. Generally, by changing the seat resonant frequencies away from the critical source vibrations such as engine or road inputs, less vibration is transferred to the seat components and therefore the BSR noise can largely be controlled in early design phase. For example, the automotive engine idling vibration transfers relatively large amount of vibration into the seat at frequencies nearly below 30 Hz. Thus, it is sometimes a wise decision, while we manage the seat resonances for the rattle noise, to keep the seat resonant frequencies e.g., above the engine idling frequency band.
Here we have used two strategies to change the seat resonant frequencies and examine the changes of the seat rattle noise. One strategy is based on increasing the stiffness of the structure and the other strategy is addition of a lumped mass (called mass/damper) to the structure (Figure 6). For these purposes, we have first used the developed seat CAE concept model and changed the seat resonant frequency. The designed modifications are then implemented in the physical model. Finally, the modifications effects are investigated on the rattle noise. The modifications of the model are examined to demonstrate the effectiveness of the concept modeling and its advantages to improve and control the rattle or in general BSR noise in the early design phase.
For increasing the stiffness of a part of the seat structure in the model, we increased the young module of the specified part (Figure 6) to change the torsion resonant frequency to 34.5 Hz. For modification of the structure
Figure 4. SPL at four selected points when the seat excited at its 31 Hz resonant frequency.
Figure 5. Comparison of the seat radiated SPLs with those of neighbouring frequencies (25 Hz and 35 Hz) when excitation frequency is equal to seat resonance frequency (31 Hz).

Figure 6. Modifications of the seat CAE model for changing the resonant frequency by increasing the stiffness (a) and addition of a mass/damper (b).
by adding mass, we have added a 1 kg lumped mass on the specified (Figure 6) point of the structure. Having used the proposed mass damper, the simulated seat torsion resonant frequency has decreased to 27.2 Hz. Comparison of the inertance FRF of the original seat CAE model with those of the modified models is shown in Figure 7. The original torsion resonant frequency (first peak) is shifted in accordance with each modification (Figure 7).
After confirming the sufficient effects of the modifications on the CAE model, the test seat is modified accordingly. For increasing the stiffness, we have welded a beam on the same part as it has done on the CAE model. For modification by mass/damper, a 1 kg mass is also added fixed (bolted) on the seat. The shifts of the torsion resonant frequency, due to the modifications, have become similar to the CAE model (Figure 8). The original 31 Hz torsion resonant frequency, obtained from experiment, has changed to 33.2 Hz and 28.5 Hz for modified seats (Figure 8).
Measurements of the original and the two modified seats radiated noises confirm that by controlling the seat structural dynamics, the rattle noise can be managed accordingly (Figure 9). When the original and the two modified seats have been excited with a 31 Hz sinusoidal input frequency, despite the original seat, the modified seats have not exhibited any significant radiated rattle noise (Figure 9). In the frequency range from 500 up to 1500 Hz SPL is decreased nearly 10 dB (Figure 9).
Figure 7. Effectiveness of the seatback stiffener and mass damper on the frequency shifting.
Figure 8. Comparison of the original seat frequency response function with modified seat (experimental results).
Figure 9. Experiment results: comparison of the original seat (before modification) radiated SPLs with those of modified seats when the seat excitation frequency is equal to resonance frequency (31 Hz).
4. Conclusions
The vehicle seat is one of the major components that have potential to be a source of annoying rattle noise. A possible analytical design method minimizes find-and-fix physical tests and provides an upfront solution for the rattle noise. Some vehicle components such as door trims exhibit a wide range of critical frequencies with no proper global mode shapes and their BSR may happen in a wide excitation frequency band. Nevertheless, the vehicle seat structure has a robust structural dynamics with identifiable vibration resonances and mode shapes. Accordingly, this paper demonstrated that controlling the seat structural dynamics is a robust upfront solution for improving the seat rattle and, in general, the seat BSR. Two experiments were conducted for this study. The first experiment was set up to characterize the seat resonant frequencies and its corresponding structural mode- shapes. The second experiment was performed to measure the seat radiated noise when it goes under vibration excitation. Alternatively, a CAE model of the seat was developed and the seat structural dynamics was characterized using the CAE model. The concept modelling method was used for the CAE modelling of the seat structure. The model was developed to allow designing the seat-structure modifications as well as predicting the effects of the modifications on the rattle noise. Comparisons of the results of the simulation and experiment validated the developed CAE model. The seat structure exhibited two major torsion and for-aft bending structural modes in low vibration frequencies (<50 Hz) where the structure has more potential to be rattled. The results of the experiments and corresponding CAE model-based simulation were consistent, so that both have exhibited two torsion and for-aft shapes.
The noise measurement results revealed that the seat generates high level of the rattle noise when the seat excitation vibration is close to the seat structure torsion resonance (here 31 Hz). We have further confirmed that the occurrence of the rattle noise is related to the seat structural dynamics and it can be controlled and managed by modifying the structure. Two modifications were designed using the seat CAE model. One modification was designed for increasing the seat torsion resonance nearly 4 Hz, and a second modification was done for decreasing the seat torsion resonance nearly 4 Hz. The designed modifications were then applied on the test seat and the rattle noise is measured on the two modified seats. The results confirmed that by changing the seat resonant frequency, the rattle noise can be changed accordingly. Consequently, for the seat system which has an identifiable structural dynamics, the rattle noise can be managed and controlled in early design phase using the seat CAE model.
Early phase modifications of the seat structure for controlling the seat rattle noise or, in general, the seat BSR noise are more robust than find-and-fix tuning of the joints or contact points associated with BSR. The modifications of the structures, for improving the BSR, manage the seat resonances and therefore transfer less vibration into the sub-components with potential for rattling. Moreover, the upfront knowledge about the seat vibration mode shapes, which contributes to the BSR noise, also assists to improve and optimize the locations of the joints associated with BSR.
References
- Rao, M.D. (2003) Recent Application of Viscoelastic Damping for Noise Control in Automobiles and Commercial Airplanes. Journal of Sound and Vibration, 262, 457-474. http://dx.doi.org/10.1016/S0022-460X(03)00106-8
- Cerrato-Jay, G., Gabiniewicz, J. and Gatt, J. (2001) Automatic Detection of Buzz, Squeak and Rattle Events. SAE Noise and Vibration Conference & Exposition, Traverse City, 30 April-3 May 2001.
- Kavarana, F. and Reiders B. (1999) Squeak and Rattle-State of the Art and Beyond. SAE Noise and Vibration Conference & Exposition, Traverse City, 17-20 May 1999.
- Gosavi, S.S. (2005) Automotive Buzz, Squeak and Rattle (BSR) Detection and Prevention. TATA Technologies Ltd., ARAI Pune, 661-667. http://dx.doi.org/10.4271/2005-26-056
- Broo, F. and Derico, J. (1995) Silicon Elastomer Reduces Noise, Vibration, and Squeaks in Vehicle Instrument Panels. SAE Technical Paper 950635.
- Fard, M.A., Ishihara, T. and Inooka, H. (2003) Transmission of the Translational Trunk Vibration to the Head-Neck Complex. JSME International Journal Series C, 46, 116-122. http://dx.doi.org/10.1299/jsmec.46.116
- Eiss, N., Lee, E. and Trapp, M. (1997) Frictional Behavior of Automotive Interior Polymeric Material Pairs. SAE Technical Paper 972056, 1479-1496.
- Shin, S. and Cheong, C. (2010) Experimental Characterization of Instrument Panel Buzz, Squeak, and Rattle (BSR) in a Vehicle. Journal of Applied Acoustics, 71, 1162-1168.
- Hagiwara, I. and Ma, Z.D. (1992) Development of Eigen mode and Frequency Response Sensitivity Analysis Methods for Coupled Acoustic-Structural Systems. JSME International Journal, Series III, 35, 229-235.
- Ma, Z.D. and Hagiwara, I. (1992) Sensitivity Calculation Method for Conducting Modal Frequency Response Analysis of Coupled Acoustic-Structural Systems. JSME International Journal, Series III, 35, 14-21.
- Nolan, S., Yao, Y., Tran, V., Weber, W. and Heard, G. (1996) Instrument Panel Squeak and Rattle Testing and Requirements. IMAC-XIV, SEM, 490-494.
- Fard, M. (2011) Structural Dynamics Characterization of the Vehicle Seat for NVH Performance Analysis. SAE Paper 01-0501.
- Lo, L., Fard, M., Subic, A. and Jazar, R. (2013) Structural Dynamic Characterization of a Vehicle Seat Coupled with Human Occupant. Journal of Sound and Vibration, 332, 1141-1152. http://dx.doi.org/10.1016/j.jsv.2012.10.010
- Donders, S., Takahashi, Y., Hadjit, R., Van Langenhove, T., Brughmans, M., Van Genechten, V. and Desmet, W. (2009) A Reduced Beam and Joint Concept Modeling Approach to Optimize Global Vehicle Body Dynamics. Finite Elements in Analysis and Design, 45, 439-455. http://dx.doi.org/10.1016/j.finel.2008.12.004
- Mundo, D., Hadjit, R., Donders, S., Brughmans, M., Mas, P. and Desmet, W. (2009) Simplified Modeling of Joints and Beam-Like Structures for BIW Optimization in a Concept Phase of the Vehicle Design Process. Finite Elements in Analysis and Design, 45, 456-462. http://dx.doi.org/10.1016/j.finel.2008.12.003
- Mundo, D., Donders, S., Hadjit, R., Stigliano, G., Mas, P. and Van der auweraer, H. (2010) Concept Modeling of Automotive Beams, Joints and Panels. Proceedings of the 3rd WSEAS International Conference on Finite Differences, Finite Elements, Finite volumes & Boundary Elements, Bucharest, 20-22 April 2010.
- Chapman, C. and Pinfold, M. (2001) The Application of Knowledge Based Engineering Approach to the Rapid Design and Analysis of an Automotive Structure, Advances in Engineering Software, 32, 903-912. http://dx.doi.org/10.1016/S0965-9978(01)00041-2
- Guyan, R. (1965) Reduction of Stiffness and Mass Matrices. AIAA Journal, 3, 380-387. http://dx.doi.org/10.2514/3.2874
- Ewins, D.J. (1984) Modal Testing, Theory and Practice. Research Studies Press, Ltd., Taunton, UK.
NOTES
*Corresponding author.











