Journal of Electronics Cooling and Thermal Control
Vol.3 No.1(2013), Article ID:29412,7 pages DOI:10.4236/jectc.2013.31005
Evaluation of Inherent Uncertainties of the Homogeneous Effective Thermal Conductivity Approach in Modeling of Printed Circuit Boards for Space Applications
Space Mechanics and Control Division/National Institute for Space Research (DMC/INPE), São José dos Campos, Brazil
Email: rafael.costa@inpe.br
Received January 28, 2013; revised March 1, 2013; accepted March 10, 2013
Keywords: PCB; Spacecraft Thermal Control; Effective Conductivity
ABSTRACT
Electronic components are normally assembled to printed circuit boards (PCBs). Such components generate heat in operation which must be conducted away efficiently from the small mounting areas to frames where the PCB is fixed. The temperature of the component depends on heat dissipation rate, technology and parameters of mounting, component placement and finally effective thermal conductivity (keff) of the board. The temperature of some components may reach significant magnitudes over 100˚C while the PCB frame is kept at near-ambient temperature. The reliability of electronic components is directly related to operating temperature, so the thermal project should be able to provide a correct temperature prediction of all PCB components under the hottest operational condition. In space applications, the main way to spread and reject heat of electronic equipment is by thermal conduction once there is no air available to apply convection-based cooling techniques. The PCB keff is an important parameter for the electronics thermal analysis when the PCB is modeled as a simplified homogeneous board with a unique thermal conductivity. In this paper, an intrinsic uncertainty of such approach is firstly reveled and its magnitude is evaluated for a real space use PCB. The simulation uses SINDA/FLUINT Thermal Desktop and aims to determine the keff of the PCB by comparison between a detailed multi-layered anisotropic model and an equivalent homogeneous single-layer model. The model was validated using available data for two-layered FR4-copper PCB. Multiple simulations are performed with different dissipating component position and mounting area.
1. Introduction
When it comes to the development of electronic equipment for space applications, there is a trend of miniaturization of the electronic components, the increase of heat dissipation per component as well as the increased density of component mounting in Printed Circuit Boards (PCB) and finally, the increase of PCB number in electronic equipment boxes.
Dissipated heat in each component causes its own temperature to rise. Depending on thermal conditions that the component is exposed, it may reach temperatures above 100˚C while the PCB frame is kept at near-ambient temperature. Such high temperature exposure can damage electronic systems in different ways. First, the electronic components may simply be burnt-out once the functional temperature limit is exceeded. Second, component parameter values usually vary with temperature and it is important not to exceed the manufacture’s temperature range defined as operational limits. Above such temperatures, the components are no longer guaranteed to be within specification, [1]. Finally, the reliability of electronic components is tremendously related to operating temperature, and according to [2], component failure rate is increased exponentially with temperature rise even within the operational limits, so lower temperatures extend the component lifetime. Thus, thermal project of the electronic equipment is an important aspect of a system’s overall design, in order to ensure that the electronic components will not violate established temperature limits and will have their operational temperature as low as possible.
It underlines the importance of an accurate thermal analysis through the design process of electronics. The PCB is a basic element of all electronic equipment, a correct prediction of temperature distribution over its area and provides the necessary information for temperature evaluation of each component mounted on the PCB. In space applications, the only way to spread and reject heat of electronic equipment is by thermal conduction over the PCB once there is no pressurized air available to use the regular convection-based cooling techniques, such as dissipating fins or fans.
In equipments and instruments for space application, PCBs are often assembled in a package where they are fitted through the perimeter to a structural frame. The frames are mounted in the equipment case in such a way that provides a good thermal contact with the equipment bas. Finally, the equipment is bolted to the satellite structural panel, where the temperature should be maintained by the satellite thermal control subsystem.
The frame structure provides a thermal conductive path from dissipating components to the equipment base surface acting as a local heat sink for each board; therefore, the temperature distribution over the PCB area can be analyzed separately, considering that the frame temperature is fixed as a boundary condition. Once we have the temperature map over the PCB, the temperature of each component can be easily obtained by local thermal balance.
Temperature over the component mounting area is strongly dependent on its thermo-physical properties. The PCB is usually manufactured in FR4 with thermal conductivity about , what is considered to be low, but the conductive traces are made of deposited copper and contribute on in-plane thermal conductivity, assisting in heat spreading from hot areas below dissipating components.
, what is considered to be low, but the conductive traces are made of deposited copper and contribute on in-plane thermal conductivity, assisting in heat spreading from hot areas below dissipating components.
In the past, PCBs used to have only one or two signal layers, but modern technologies have allowed the production of very complex PCBs that have several intermediate conductive layers. Such arrangement makes thermal properties of those PCBs strongly anisotropic.
The temperature map over the PCB could be obtained by the use of numerical methods available through some commercial software such as ANSYS Iceboard (former TASPCB), HyperLynx Thermal (Former BETAsoft), FLOTHERM.PCB, SINDA/FLUINT Thermal Desktop, ESATAN and others, or even by analytical methods [3, 4].
However, almost all of the methods are based on the assumption that the multi-layer PCB can be thermally represented by an equivalent homogeneous plate with certain effective thermal conductivity (keff) that could provide the same thermal effect as a real multi-layer PCB with anisotropic properties.
In this context, thermal modeling of heat conduction in multi-layer boards is occasionally simplified by using the keff concept. Such parameter combines the influences of individual layer conductivities into a single value that can be applied as if the board had only one homogeneous layer where overall thickness and surface area are preserved.
Some analytical methods have been proposed to calculate keff, where arithmetic mean, geometric mean and harmonic mean are among them. All of these methods are based on the cross-plane conductivity (series) and the in-plane conductivity (parallel) are generally considered to be the lower and upper limits for the keff respectively, but the difference between their values can reach 10 times. This paper also aims to contribute on how to estimate the keff of a typical multilayer PCB for space applications by direct numerical simulation. The uncertainty of such method is evaluated.
2. Thermal Effective Conductivity Determination of PCBs
2.1. Canonical Methods
According to [5], the parameter thermal effective conductivity used in PCB thermal analysis could be determined by the use of simplified analytical methods, where keff is calculated based on the cross-plane conductivity (ks) with resistances in series and the in-plane conductivity (kp) with resistances in parallel, Equations (1) and (2).
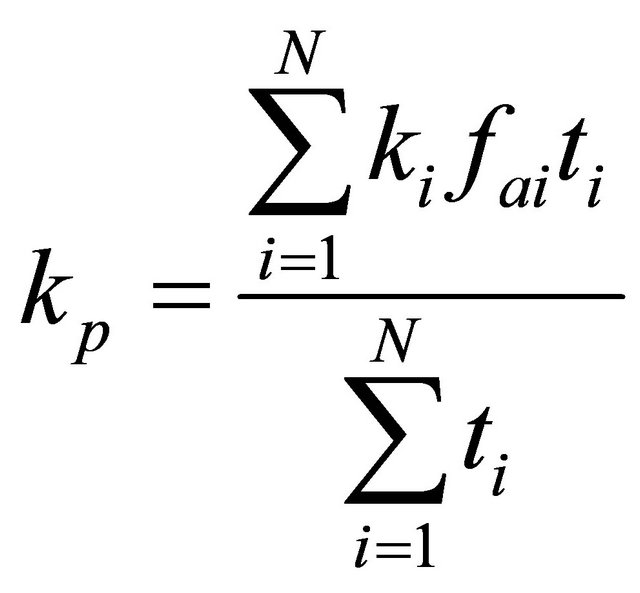 (1)
(1)
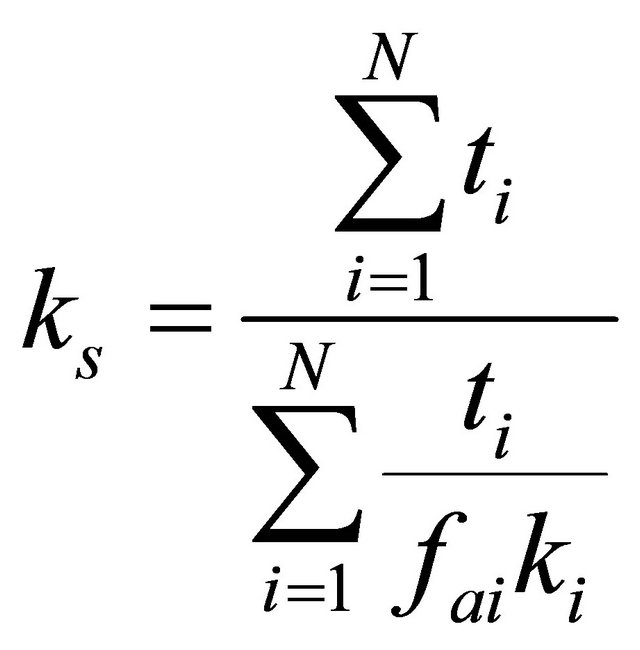 (2)
(2)
where:
ti: layer thickness (m)
ki: layer thermal conductivity (W/m˚C)
fai: copper covering area factor The concept of the isotropic effective thermal conductivity is usually introduced as a unique homogeneous property keff as a function of ks and kp. Several combinations of these parameters are commonly used to determine the value of keff, such as arithmetic mean, geometric mean and harmonic mean. Figure 1 shows the simple laminated structure assumed to represent the PCB.
This approach is extremely easy to use, but provides results with uncertainties of order of 10 times, which is unacceptable in electronics thermal analysis, particularly for space applications.
2.2. Numerical Simulation Method
The method consists of creating a conjugate pair of a detailed and a simplified model that represent the same PCB layout and afterwards comparing them. The detailed model is constructed as a multi-layer board wherein each of the layers has the same thickness and thermal conductivity

Figure 1. Simplification of the PCB laminated structure.
as in the real PCB. Each signal layer with copper traces is treated as a homogeneous layer with an equivalent thermal conductivity equal to the copper conductivity weighted by the fraction of the area covered with copper. The covering area was estimated by a pixel count technique based on a CAD design of the PCB.
On the other hand, the simplified model is a singlelayer board, which thickness is obtained by summing all the layers thicknesses of the detailed model, with a unique thermal conductivity value called effective thermal conductivity (keff). The same boundary conditions and heat loads are applied both to the detailed and simplified models. Figure 2 shows the both models configurations.
Initially, we execute the simulation for the detailed model where the component (heat source) will reach certain temperature in steady state regime. After that, we run several simulations using the simplified model modifying the board’s conductivity until the component reaches the same temperature as in the complex model. Equation (3) mathematically describes the process, where the temperature difference in the component must be minimized by changing the value of keff.
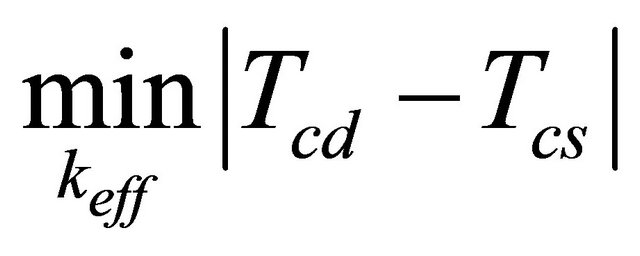 (3)
(3)
When the temperature difference is less than 0.1˚C, it is considered that the minimum was reached and this conductivity can represent the effective thermal conductivity of the detailed model.
2.3. Theoretical Basis
Let us consider the theoretical relations behind the use of the homogeneous conception in the PCB thermal analysis. In a typical PCB, the main heat path between a dissipating component and a heat sink frame can be simplified as shown in Figure 3. The heat passes along the in-plane direction (which has the maximum thermal conductivity —kp) and then goes down to a frame area in the crossplane direction (which has the minimum thermal conductivity—ks).
In such models, it is intended to approach this mechanism as a homogeneous passage through an artificial Detailed Model
Simplified Model
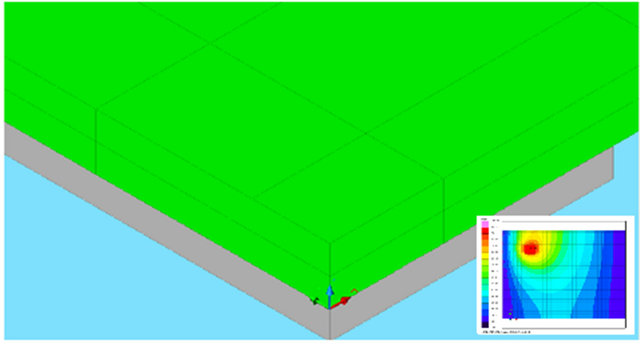
Figure 2. Detailed and simplified models configuration.

Figure 3. Heat path between the dissipating component and the cold frame.
media with an equivalent effective thermal conductivity keff. This equivalency comes from the equality of the conductance per unit of PCB Ly length, Equation (4).
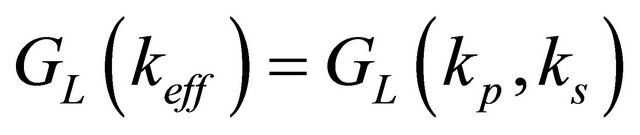 (4)
(4)
For this simplified geometry,
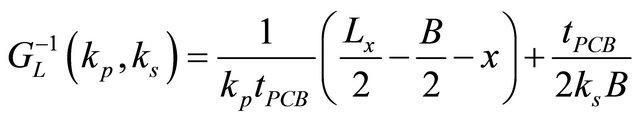 (5)
(5)
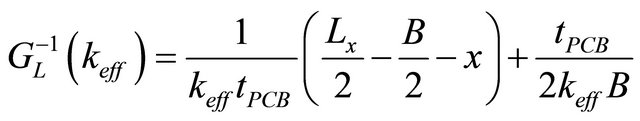 (6)
(6)
where:
GL: isotropic conductance (W/˚C)tPCB: board thickness (m)B: frame width (m)Lx: board horizontal lengthLy: board vertical lengthx: distance between the board center and the dissipating component.
In Equation (5), the two terms correspond to the thermal resistances of the heat paths along and normal to the surface from the dissipating electronic component to the frame. Equation (6) represents the same resistances as a function of keff.
Resolving Equation (4), with substitution (5) and (6) we have:
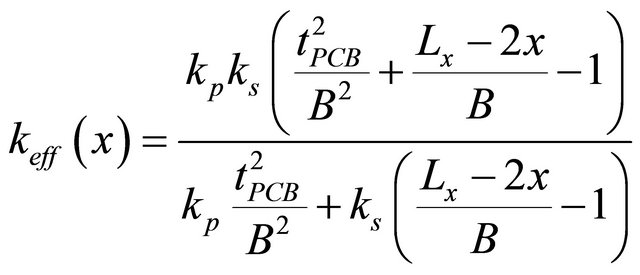 (7)
(7)
All dimensions are related to the frame width B. Therefore it is possible to use relative lengths instead, Equation (6).
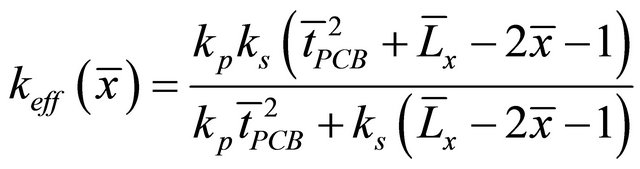 (8)
(8)
The parameter keff is a function of x, i.e. its value varies with x.
Equation (6) will never be independent of x once kp and ks are different, i.e. the uncertainty is intrinsic to this approach when an anisotropic PCB is approximated by an isotropic model.
We could even evaluate the limits of the keff variation considering the entire area where the components could be mounted, Equation (7).
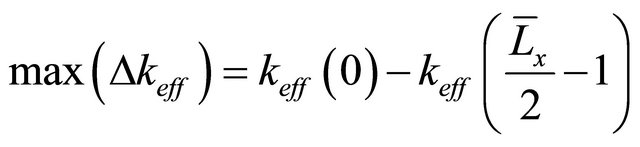 (9)
(9)
After substituting, we have:
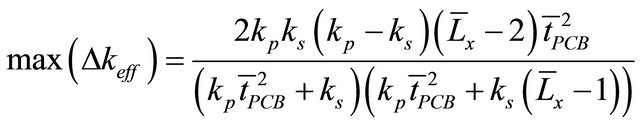 (10)
(10)
This equation represents the theoretical range of the intrinsic uncertainty for the homogeneous board approach.
3. Space Use PCB with 6 Copper Layers
The PCB sample used for the analysis was a 160 mm × 215 mm × 2 mm, consisted by 6 signal layers (conductive): top, grounding, power, inner 1, inner 2 and bottom. Each layer has a certain percentage of copper and a fiberglass reinforced epoxy (FR4) is used as a dielectric material between layers; photographs of the PCB are shown in Figure 4.
From the board’s project we can see the 6 signal layers TOP

BOTTOM

Figure 4. External layers of the PCB used in satellite equipment.
in Figure 5. The copper coverage has been estimated for each signal layer in order to apply a percentage factor (fa) over the copper thermal conductivity (kcu = 400 W/mK) in the model.
As previously done, 2 equivalent models were created, a detailed (11 layers) and a simplified (1 layer). The only boundary condition imposed to the model were two 10 mm wide frame kept at constant temperature of 20˚C, which were placed at the bottom surface with heat transfer coefficient of 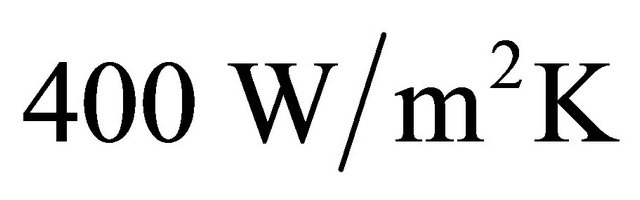 as contact condition. Several mesh configurations have been tested with gradual refining in order to get stable results that were achieved by setting 30 × 30 × 2 edge type nodes for all board layers with
as contact condition. Several mesh configurations have been tested with gradual refining in order to get stable results that were achieved by setting 30 × 30 × 2 edge type nodes for all board layers with  for the contact between them. Table 1 shows the layer composition of the detailed model, each of the signal layers with conductive traces was treated as a homogeneous layer with an equivalent thermal conductivity equal to copper conductivity (400 W/mK) multiplied by the percentage of copper covering area, which was estimated by a pixel count technique based on the PCB’s electrical project.
for the contact between them. Table 1 shows the layer composition of the detailed model, each of the signal layers with conductive traces was treated as a homogeneous layer with an equivalent thermal conductivity equal to copper conductivity (400 W/mK) multiplied by the percentage of copper covering area, which was estimated by a pixel count technique based on the PCB’s electrical project.
For the heat load, a 2 W dissipating component was created in 3 size configurations: 10 × 8 mm, 20 × 8 mm and 20 × 16 mm with 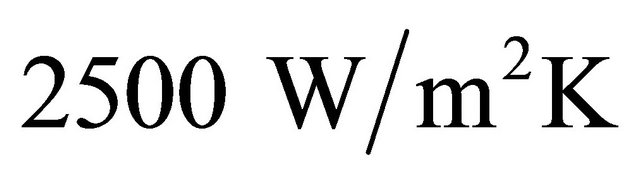 for the contact conductance with the top board surface. Such component has been placed in 13 different locations, see Figure 6.
for the contact conductance with the top board surface. Such component has been placed in 13 different locations, see Figure 6.
The positioning coordinates are presented at Table 2, considering the lower left corner as the origin (0,0).
TOP GND
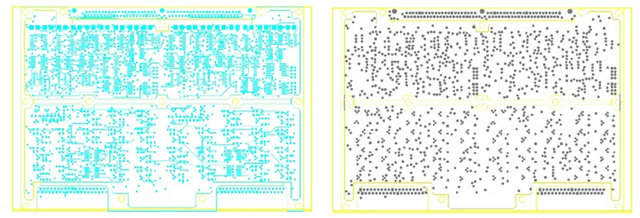
INNER 1 POWER
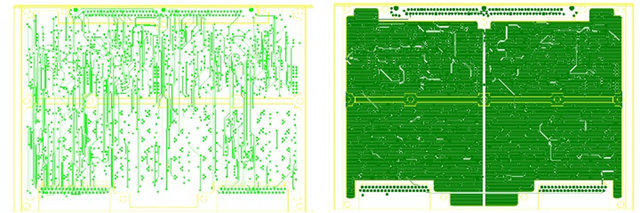
INNER 2 BOTTOM

Figure 5. Layout of the 6 copper layers.
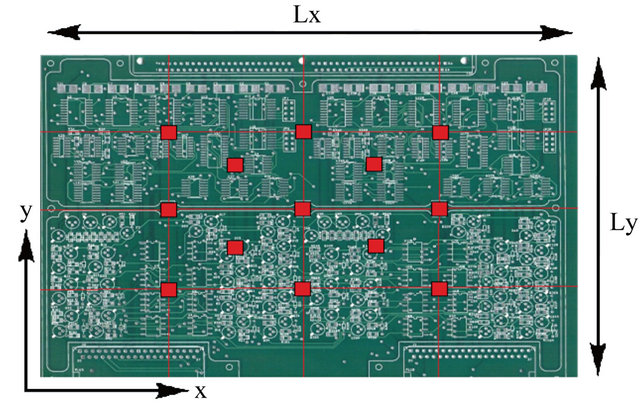
Figure 6. Component positioning over the PCB.
Table 1. Detailed model composition.
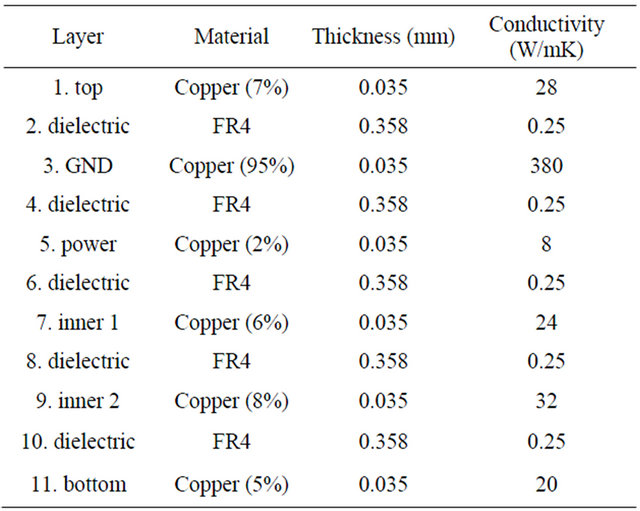
Table 2. Component position over the board.

4. Results and Discussions
We run the simulation for the 13 positioning cases changing the component size three times, which generated the results for effective conductivity mean for each component position and its standard deviation, presented in Table 3.
It is observed that the uncertainty due to the influence of component size is approximately ±3.2%, which is considered quite small and will be always adjusted according to the mounting technique.
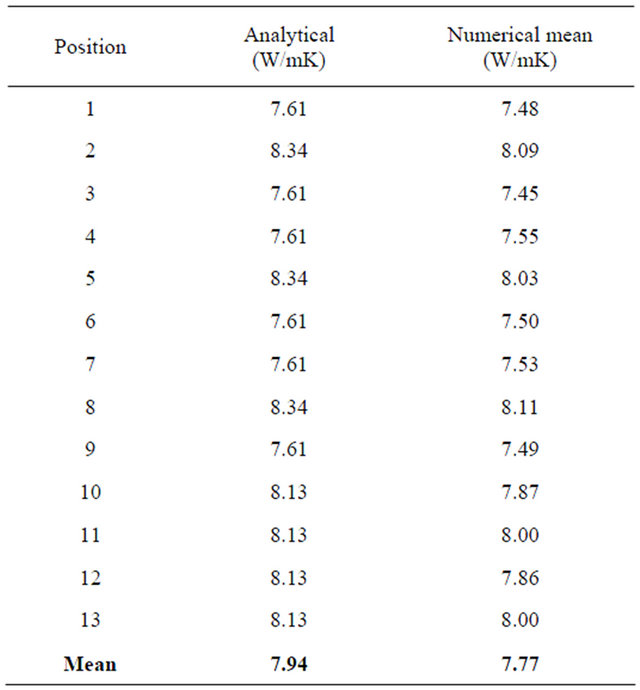
Theoretical values were also calculated using Equation (7) for the same positions. The analytical and numerical simulation results are presented in Table 4.
In order to get aware of any tendencies in our data, we have placed the origin of the system at the board’s center and plotted the mean of the adjusted keff against the component’s horizontal position (x axis), thereby generating the chart presented in Figure 7. The analytical values extracted from Equation (7) are also plotted for comparison. The deviation between the numerical simulation and the analytical evaluation is 2.1%.
In Figure 7 there is a clear tendency of keff to be higher when the dissipative element is placed at the center of the PCB and consequently far from the frames. It fits the theoretical trend by Equation (7), and keff has its maximum magnitude when x is 0 (at the center).
This tendency occurs because the detailed model has several layers and its conductivity becomes anisotropic. When the element is positioned near the frames with fixed temperature, its keff is more affected by the crossplane ks than the in-plane kp. Since kp > ks, the isotropic keff near the frames is artificially reduced.
This study demonstrates an important conclusion that for the use of a model with isotropic thermal conductivity
Table 3. Results for the isotropic keff obtained after the model adjustment.

Table 4. Theoretical and simulation values of keff for the analyzed sample.
one should use the additional margin of uncertainty to the keff values due to the component placement influence in the case that the boundary conditions represent the fixation of the board on frames, which is very typical in electronic equipment for space use. For the component positions, presented in Figure 6 by red marks, the uncertainty is about ±6.5%. If entire available PCB area would be used for the component mounting, the uncertainty may
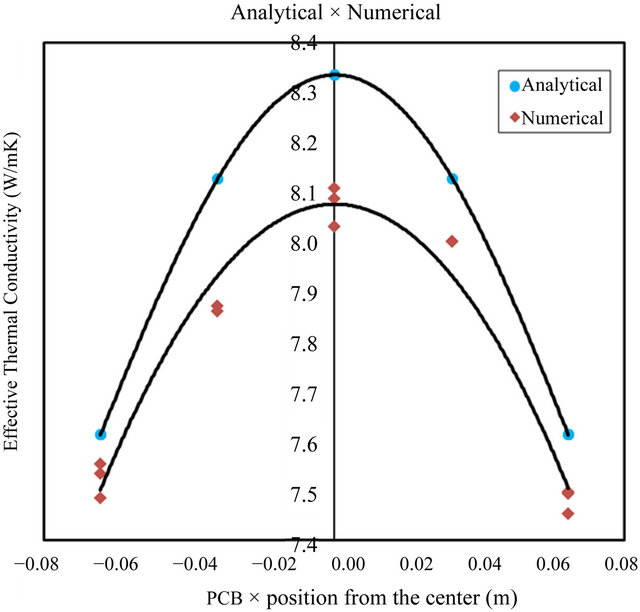
Figure 7. Effective thermal conductivity mean against the horizontal position of the component.
reach the theoretical value of ±24.3%, according to Equation (10).
4. Conclusions
The study firstly revealed an intrinsic uncertainty in the keff value when using the homogeneous isotropic model approach to thermally analyze electronic equipment at the PCB level for space use.
Based on the results presented, we could clearly confirm that the effective thermal conductivity has a decreasing tendency as further the component is placed from the center of the board, i.e. close to the heat sink frame. This tendency occurs because the detailed model has an anisotropic thermal behavior, so when the element is placed near the frames, its keff is more affected by the ks than the kp. The keff value is artificially reduced because kp > ks. When using an isotropic keff model, a ±6.5% uncertainty margin should be considered if the boundary conditions are found in space applications, where the PCB is fixed to frames on its perimeter. The maximum theoretical uncertainty for this PCB is ± 24.3%.
Also, it was observed that the uncertainty due to the influence of component size is approximately ±3.2%, which could be also considered, but is less important.
Developed analytical expression (Equation (10)) may be used to roughly estimate the maximal inherent uncertainty for frame-installed PCBs for space use.
5. Acknowledgements
The authors would like to thank the support of the Space Mechanics and Control Division—DMC of ETE (General Coordination of Engineering and Space Technology) of the National Institute for Space Research—INPE.
REFERENCES
- M. Carchia, “Electronic/Electrical Reliability,” Carnegie Mellon University, Pittsburgh, 1999.
- R. Remsburg, “Thermal Design of Electronic Equipment,” CRC Press, London, 2001.
- V. V. Vlassov, “Analytical Model of the Two-Dimensional Temperature Distribution over a Single Electronic Circuit Board,” Reterm—Thermal Engineering (Engenharia Térmica), Vol. 3, 2003, pp. 32-37.
- V. V. Vlassov, “A Tool for Thermal Analysis of Electronic Boards with Multiple Heat Sources and Sinks,” SAE Paper 2005-01-3058, 2005. http://www.sae.org/technical/papers/2005-01-3058
- J. R. Culham, P. Teertstra and M. M. Yovanovich, “The Role of Spreading Resistance on Effective Conductivity in Laminated Substrates,” Future Circuits, Vol. 6, 2000, pp. 73-78.

