Advances in Materials Physics and Chemistry
Vol.05 No.08(2015), Article ID:58795,8 pages
10.4236/ampc.2015.58031
Dependence of the Structure, Optical Phonon Modes and Dielectric Properties on Pressure in Wurtzite GaN and AlN
Huanyou Wang1*, Yaqi Chen1, Yalan Li1,2, Xiangyan He1
1Department of Physics and Electronic Information Engineering, Xiangnan University, Chenzhou, China
2College of Physical Science and Technology, Huazhong Normal University, Wuhan, China
Email: *whycs@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 June 2015; accepted 11 August 2015; published 14 August 2015
ABSTRACT
The density functional perturbation theory (DFPT) is employed to study the structure, optical phonon modes and dielectric properties for wurtzite GaN and AlN under hydrostatic pressure. In order to calculate accurately the Born effective charges and high frequency dielectric tensors, we utilize two sum rules to monitor this calculation. The calculated optical phonon frequencies and longitudinal-transverse splitting show an increasing with pressure, whereas the Born effective charges and high frequency dielectric tensors are found to decrease with pressure. In particular, we analysed the reason for discrepancy between this calculation and previous experimental determination of pressure dependence of the LO-TO splitting in AlN. The different pressure behavior of the structural and lattice-dynamical properties of GaN and AlN is discussed in terms of the strengths of the covalent bonds and crystal anisotropy. Our results regarding dielectric Grüneisen parameter are predictions and may serve as a reference.
Keywords:
GaN AlN, Lattice Dynamics, Dielectric, Pressure

1. Introduction
The group-III nitrides GaN and AlN are currently being actively investigated in view of their promising potential for short-wavelength electroluminescence devices and high-temperature, high-power, and high-frequency electronics [1] - [5] . An important motivation for high-pressure investigations stems from the fact that group-III- nitride layers are commonly subjected to large built-in strain since they are often grown on different substrates having considerable lattice mismatch.
The understanding the effect of pressure on the vibrational properties is quite important. Its knowledge allows one to correlate macroscopic thermodynamic parameters with properties on the atomic scale. The neutron scattering, electron energy loss spectroscopy, IR absorption, Raman spectroscopy, and diamond anvil cell etc. experimentally have been used to study phonons and related properties. Perlin et al. [6] and Kuball et al. [7] performed the high-pressure Raman studies for AlN, estimating the pressure coefficients of Raman-active modes. They reported that under pressure, the LO-TO (E1) splitting slightly decreased and the LO-TO (A1) splitting increases. Afterwards, Goñi et al. [8] compared the pressure dependence of the Raman-active modes in GaN and AlN with ab initio calculations and found a small but increasing LO-TO (E1) splitting under pressure. However, a decrease of the LO-TO splitting for both A1 and E1 modes in AlN was estimated in recent Raman measurements of Yakovenko et al. [9] and Francisco et al. [10] . Meanwhile, Francisco et al. studied the optical phonon modes and pressure dependences of AlN by means of ab initio lattice dynamical calculations, but being a increase of the LO-TO splitting for both A1 and E1 modes. Perlin et al. [11] compared pressure dependence of the A1 (TO), A1 (LO) phonon modes and effective transverse charge of wurtzite GaN by Raman scattering and means of tight-binding formalism. In contrast with the extensive range of experimental studies on the pressure effect on the phonon dispersion of semiconductors, theoretical works on the topic are relatively sparse. The pressure dependence of the LO-TO splitting in GaN and AlN is an issue of controversy. In a polar lattice, the splitting of the optical phonon modes is determined by two parameters, Born effective charge of the lattice ions and the screening of the Coulomb interaction, which depends on the electronic part of the dielectric constant in the phonon frequency regime.
In this work, we study the pressure effect on phonon and relevant properties for GaN up to 50 GPa and AlN up to 20 GPa by DFPT computations. Firstly, we calculate and analyse the evolution with pressure of the unit cell shape (i.e., c/a ratio) and unit cell geometry (i.e., internal parameter u) of GaN and AlN. In the following section, it will study pressure dependence of zone-center optical phonon modes and the LO-TO splitting of both the A1 and E1 modes. Next, it will calculate and discuss the pressure dependence of Born effective charge tensors 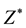 and the high frequency dielectric tensor
and the high frequency dielectric tensor . Finally, it will predict dielectric Grüneisen paramete
. Finally, it will predict dielectric Grüneisen paramete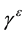 .
.
2. Theory and Computational Details
2.1. Theory
The interatomic force constants (IFC’s) describing the atomic interactions in a crystalline solid are defined in real space as [12]
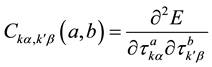 (1)
(1)
Here,  is the displacement vector of the kth atom in the ath primitive unit cell (with translation vector
is the displacement vector of the kth atom in the ath primitive unit cell (with translation vector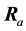 ) along the α axis. E is the Born-Oppenheimer (BO) total energy surface of the system (electrons plus clamped ions).
) along the α axis. E is the Born-Oppenheimer (BO) total energy surface of the system (electrons plus clamped ions).
The vibration frequencies 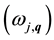 and polarization vectors
and polarization vectors 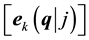 of the phonon modes with wave vec-
of the phonon modes with wave vec-
tor 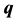 are determined by solving the eigenvalue matrix equation
are determined by solving the eigenvalue matrix equation
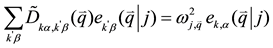 (2)
(2)
where 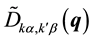 is the dynamical matrix, which is related to the Fourier transform of the IFC’s.
is the dynamical matrix, which is related to the Fourier transform of the IFC’s.
The dielectric constant mainly is influenced by two factors which are the electron and phonon,
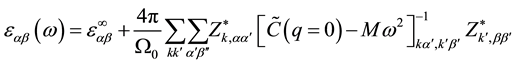 , (3)
, (3)
where 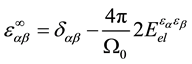 is electronic contribution to the dielectric constant;
is electronic contribution to the dielectric constant; 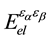 is the second deriva-
is the second deriva-
tive of the total electronic energy with respect to a perturbing electric field along directions α and β; 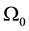 and M are the unit cell volume and mass; to other variables, see Ref. [12] .
and M are the unit cell volume and mass; to other variables, see Ref. [12] .
The Born effective charge is defined as the variation of the force on a given atom under the application of an electric field
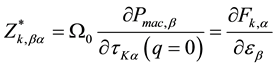 (4)
(4)
where 

The second sum rule guarantees that the charge neutrality is also fulfilled at the level of the Born effective charges. For every direction 


By the above sum rules, we can monitor whether the calculation is well converged with respect to numerical parameters, like the number of plane waves, the sampling of BZ, and the number of points of the exchange-correlation grid.
2.2. Computational Details
We use a first-principles pseudopotential method base on the density functional perturbation theory with wave function represented in a plane-wave basis set. This work is performed employing the ABINT package [13] . A review of the method (and of the algorithm used for the convergence of electronic density and atomic positions) can be found in Ref. [14] . The effect of the approximation to the exchange-correlation (XC) energy is considered. The pseudopotential for Ga, Al and N atoms are generated according to scheme of Troullier and Martin [15] . Brillouin-zone integrations were performed using 12 × 12 × 8 k-point mesh, and phonon frequencies were computed on a 6 × 6 × 4 q-point mesh. Plane-wave basis sets with a cutoff of 40 Hartree were used. These calculating parameters are chosen to guarantee the total energy error in 0.1 mHartree.
3. Results and Discussion
In Figure 1, we show the evolution with pressure of the unit cell shape (i.e., c/a ratio) and unit cell geometry (i.e., internal parameter u) of the wurtzite structure GaN and AlN.
The calculations were performed in two steps. In the first step, we calculate the total energy of the bulk wurtzite crystal as a function of the unit cell volume. Then, using the definition of pressure, 
ficients of 

is completely different. The values c/a (u) are remarkably smaller (larger) than the ideal values and decrease
(increase) with rising hydrostatic pressure, with a slope of 

× 10−4. Our results for c/a are in reasonable agreement with experimental studies of the lattice constants under pressure [16] [17] .
For most stable wurtzite-type structures c/a ratio and the u parameter are strongly correlated; If c/a decreases, then u increases in such a way that the inequivalent bond lengths R(1) (along the c direction with bond length


Figure 1. Structural parameters of wurtzite GaN and AlN under hydrostatic pressure. Asterisk and open circles are experimental results from Ref. [16] for GaN and Ref. [17] for AlN.
(in the hexagonal plane and is threefold degenerate with bond length

with the calculated one (0.3745). In the case of AlN there is, however, a larger deviation between the estimated value (0.3784) and the calculated one (0.3803). This finding can be attributed to the stronger covalent bonding of AlN, which preserves the ideal tetrahedral bond angles.
The pressure dependence of zone-center optical phonon modes and the LO-TO splitting of both the A1 and E1 modes are plotted in Figure 2 (GaN) and Figure 3 (AlN). Table 1 summarizes fitting pressure coefficients of the A1 and E1. In general, the agreement between our calculated values at zero pressure and other theoretical values [8] is reasonably good. The calculated frequencies are slightly above other experimental data, which is likely due to underestimation of the lattice parameters as is usual in DFT-LDA calculations. Also, the calculated pressure coefficients are typically smaller than other experimental values. Also interesting is the difference between the pressure dependence of the LO-TO splittings in AlN. According to our calculations both the LO-TO splitting of both the A1 and E1 modes are almost constant or even increase slightly with increasing pressure. An increase of the LO-TO splitting for the A1 mode was found Manjόn et al. [18] and Goñi et al. [8] and attributed to the decrease of the refractive index with pressure in AlN as suggested by ab initio calculations [19] . The experimental discrepancies could be due to differences in sample preparation and pressure environment that may affect the pressure response of the Raman modes in AlN [9] . Additionally, the weak intensity of the TO and LO modes reported by Kuball et al. [7] might have resulted in an inaccurate determination of the pressure coefficients and LO-TO splittings.
Taking the angular dispersion of the TO modes, 
The LO-TO splitting is a function of Born effective charges Z* and infrared dielectric constant

where 

Figure 2. The zone-center optical frequencies for the wurtzite GaN as functions of pressure (upper panel). Pressure dependence of the LO-TO splitting for both the A1 and E1 modes in GaN (lower panel). Open circles and asterisk are taken from experimental results for A1 from Ref. [11] and Ref. [8] for GaN respectively.
Figure 3. The zone-center optical frequencies for the wurtzite AlN as functions of pressure (upper panel). Pressure dependence of the LO-TO splitting for both the A1 and E1 modes in AlN (lower panel). Open circles and asterisk are taken from experimental results for A1 and E1 from Ref. [10] for AlN respectively.
modes. It is a measure of the change in electronic polarization due to ionic displacements. For atom k, 
Although there are four atoms in the unit cell of the wurtzite structure the nonsymmorphic space group 
Table 1. Fitting parameters used for the pressure dependence of the phonon frequencies in GaN and AlN . For comparison theoretical and experimental results in other literatures are also shown.
aThis work, bRef. [8] , cRef. [11] , dRef. [8] , eRef. [7] , fRef. [10] , gRef. [9] , hRef. [8] .
acoustic sum rule:


tensor are existent. Contrary to the effective charges, the form of the dielectric tensor is determined by the symmetry of the crystal and is expected to be diagonal for the wurtzite structure. The dielectric tensors 


The calculated Born effective charge tensors at zero pressure agree well with the experimental data obtained from first-order Raman-scattering experiments [21] . To the best of our knowledge, no other experimental data of the Born effective charge tensors for GaN and AlN exist. The calculated Born effective charges 

Our results concerning 

The average value 
The pressure dependence of 




to characterize the pressure dependence of the dielectric constants. For GaN and AlN, we have found that the
perpendicular and parallel components of 




4. Conclusion
In summary, first-principles calculations in the framework of the DFPT are carried out to study the pressure
Figure 4. Born effective charge versus pressure for wurtzite GaN and AlN.
Figure 5. High-frequency dielectric constant versus pressure for wurtzite GaN and AlN.
dependences of structure, phonon and dielectric properties for wurtzite GaN and AlN. Our results show that pressure dependence of the wurtzite parameters c/a are reasonably well, as measured by high pressure X-Ray diffraction studies. The calculated pressure dependence of optical phonon frequencies, Born effective charges, dielectric constants is agreement with other theoretical data available. However, the calculated pressure coefficients of optical phonon frequencies are smaller than other experimental values, and pressure dependence of the LO-TO splittings in AlN between calculated and experimental data is contrary. The pressure dependence of



Cite this paper
HuanyouWang,YaqiChen,YalanLi,XiangyanHe, (2015) Dependence of the Structure, Optical Phonon Modes and Dielectric Properties on Pressure in Wurtzite GaN and AlN. Advances in Materials Physics and Chemistry,05,316-324. doi: 10.4236/ampc.2015.58031
References
- 1. Schubert, E.F. and Kim, J.K. (2005) Solid-State Light Sources Getting Smart. Science, 308, 1274-1278.
http://dx.doi.org/10.1126/science.1108712 - 2. Kuykendall, T., Ulrich, P., Aloni, S. and Yang, P. (2007) Complete Composition Tunability of InGaN Nanowires Using a Combinatorial Approach. Nature Materials, 6, 951-956.
http://dx.doi.org/10.1038/nmat2037 - 3. Simon, J., Protasenko, V., Lian, C., Xing, H. and Jena, D. (2010) Polarization-Induced Hole Doping in Wide—Band-Gap Uniaxial Semiconductor Heterostructures. Science, 327, 60-64.
http://dx.doi.org/10.1126/science.1183226 - 4. Dong, L., Yadav, S.K., Ramprasad, R. and Alpay, S.P. (2010) Band Gap Tuning in GaN through Equibiaxial In-Plane Strains. Applied Physics Letters, 96, Article ID: 202106.
http://dx.doi.org/10.1063/1.3431290 - 5. Wang, H.Y., Xu, H., Huang, T.T. and Deng, C.S. (2008) Thermodynamics of Wurtzite GaN from First-Principle Calculation. The European Physical Journal B, 62, 39-43.
http://dx.doi.org/10.1140/epjb/e2008-00121-2 - 6. Perlin, P., Polian, A. and Suski, T. (1993) Raman-Scattering Studies of Aluminum Nitride at High Pressure. Physical Review B, 47, 2874-2879.
http://dx.doi.org/10.1103/PhysRevB.47.2874 - 7. Kuball, M., Hayes, J.M. and Prins, A.D. (2001) Raman Scattering Studies on Single-Crystalline Bulk AlN under High Pressures. Applied Physics Letters, 78, 724-726.
http://dx.doi.org/10.1063/1.1344567 - 8. Goni, A.R., Siegle, H., Syassen, K., Thomsen, C. and Wagner, J.M. (2001) Effect of Pressure on Optical Phonon Modes and Transverse Effective Charges in GaN and AlN. Physical Review B, 64, Article ID: 035205.
http://dx.doi.org/10.1103/PhysRevB.64.035205 - 9. Yakovenko, E.V., Gauthier, M. and Polian, A. (2004) High-Pressure Behavior of the Bond-Bending Mode of AIN. JETP, 98, 981-985.
http://dx.doi.org/10.1134/1.1767565 - 10. Manjón, F.J., Errandonea, D., Romero, A.H., Garro, N., Serrano, J. and Kuball, M. (2008) Lattice Dynamics of Wurtzite and Rocksalt AlN under High Pressure: Effect of Compression on the Crystal Anisotropy of Wurtzite-Type Semiconductors. Physical Review B, 77, Article ID: 205204.
http://dx.doi.org/10.1103/physrevb.77.205204 - 11. Perlin, P., Suski, J. and Ager, W. (1999) Transverse Effective Charge and Its Pressure Dependence in GaN Single Crystals. Physical Review B, 60, 1480-1483.
http://dx.doi.org/10.1103/PhysRevB.60.1480 - 12. Gonze, X. and Lee, C. (1997) Dynamical Matrices, Born Effective Charges, Dielectric Permittivity Tensors, and Interatomic Force Constants from Density-Functional Perturbation Theory. Physical Review B, 55, 10355-10368.
http://dx.doi.org/10.1103/PhysRevB.55.10355 - 13. Gonze, X., Beuken, J.M. and Caracas, R. (2002) First-Principles Computation of Material Properties: The ABINIT Software Project. Computational Materials Science, 25, 478-492.
http://dx.doi.org/10.1016/S0927-0256(02)00325-7 - 14. Payne, M.C., Teter, M.P., Allan, D.C., Arias, T.A. and Jonannopoulos, J.D. (1992) Iterative Minimization Techniques for Ab initio Total-Energy Calculations: Molecular Dynamics and Conjugate Gradients. Reviews of Modern Physics, 64, 1045-1097.
http://dx.doi.org/10.1103/RevModPhys.64.1045 - 15. Troullier, N. and Martins, J.L. (1991) Efficient Pseudopotentials for Plane-Wave Calculations. Physical Review B, 43, 1993-2006.
http://dx.doi.org/10.1103/PhysRevB.43.1993 - 16. Ueno, M., Onodera, A., Shimomura, O. and Takemura, K. (1992) X-Ray Observation of the Structural Phase Transition of Aluminum Nitride under High Pressure. Physical Review B, 45, 10123-10126.
http://dx.doi.org/10.1103/PhysRevB.45.10123 - 17. Ueno, M., Yoshida, M., Onodera, A., Shimomura, O. and Takemura, K. (1994) Stability of the Wurtzite-Type Structure under High Pressure: GaN and InN. Physical Review B, 49, 14-21.
http://dx.doi.org/10.1103/physrevb.49.14 - 18. Manjón, F.J., Errandonea, D., Garro, N., Romero, A.H., Serrano, J. and Kuball, M. (2007) Effect of Pressure on the Raman Scattering of Wurtzite AlN. Physica Status Solidi (b), 244, 42-47.
- 19. Wagner, J.M. and Bechstedt, F. (2002) Properties of Strained Wurtzite GaN and AlN: Ab initio Studies. Physical Review B, 66, 115202.
http://dx.doi.org/10.1103/PhysRevB.66.115202 - 20. Venkataraman, G., Feldkamp, L.A. and Sahni, V.C. (1975) Dynamics of Perfect Crystals. MIT Press, Cambridge, Massachusetts, 202.
- 21. Sanjurjo, J.A., Lopez-Cruz, E., Vogl, P. and Cardona, M. (1983) Dependence on Volume of the Phonon Frequencies and the IR Effective Charges of Several III-V Semiconductors. Physical Review B, 28, 4579-4584.
http://dx.doi.org/10.1103/PhysRevB.28.4579 - 22. Xu, Y.N. and Ching, W.Y. (1993) Electronic, Optical, and Structural Properties of Some Wurtzite Crystals. Physical Review B, 48, 4335-4351.
http://dx.doi.org/10.1103/PhysRevB.48.4335 - 23. Bungaro, C., Rapcewicz, K. and Bernholc, J. (2000) Ab initio Phonon Dispersions of Wurtzite AlN, GaN, and InN. Physical Review B, 61, 6720-6725.
http://dx.doi.org/10.1103/PhysRevB.61.6720 - 24. Christensen, N.E. and Gorczyca, I. (1994) Optical and Structural Properties of III-V Nitrides under Pressure. Physical Review B, 50, 4397-4415.
http://dx.doi.org/10.1103/PhysRevB.50.4397 - 25. Karch, K. and Bechstedt, F. (1997) Ab initio Lattice Dynamics of BN and AlN: Covalent versus Ionic Forces. Physical Review B, 56, 7404-7415.
http://dx.doi.org/10.1103/PhysRevB.56.7404 - 26. Gorczyca, I., Christensen, N.E., Pelzery Blancá, E.L. and Rodriguez, C.O. (1995) Optical Phonon Modes in GaN and AlN. Physical Review B, 51, 11936-11939.
http://dx.doi.org/10.1103/PhysRevB.51.11936
NOTES
*Corresponding author.








