Advances in Materials Physics and Chemistry
Vol.3 No.2(2013), Article ID:32650,14 pages DOI:10.4236/ampc.2013.32018
Structure and Thermoelectric Properties of Nanostructured (Bi, Sb)2Te3 (Review)
1Department of semiconductor materials, Giredmet Ltd., Moscow, Russia
2Department of functional and structural materials, Technological Institute of Superhard and New Carbon Materials, Troitsk, Russia
3Department of dielectric and semiconductor materials, National University of Science and Technology “MISIS”, Moscow, Russia
Email: *girlab22@mail.ru
Copyright © 2013 Igor A. Drabkin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 23, 2013; revised May 3, 2013; accepted May 15, 2013
Keywords: Solid Solutions (Bi, Sb)2Te3 P-Type; Nanostructure; Spark Plasma Sintering; Conductivity; Hall Effect; Hole Free Path; Seebeck Coefficient; Thermal Conductivity; Figure of Merit
ABSTRACT
The investigation of the structure and thermoelectric properties of nanostructured solid solutions (Bi, Sb)2Te3 p-type has been carried out. The samples were obtained by grinding of original compositions in a planetary ball mill and by spark plasma sintering (SPS). Initial powder has an average particle size of 10 - 12 nm according to transmission electron microscopy, and the size of the coherent scattering region (CSR) obtained by X-ray line broadening. During sintering at Ts = 250˚C - 400˚C, the grain size and CSR increased, which was associated with the processes of recrystallization. The maximum of size distribution of CSR shifts to larger sizes when Ts increases so that no broadening of X-ray lines at Ts = 400˚C can take place. At higher Ts, the emergence of new nanograins is observed. The formation of nanograins is conditioned by reducing of quantity of the intrinsic point defects produced in the grinding of the source materials. The study of the electrical conductivity and the Hall effect in a single crystal allows to estimate the mean free path of the holes-L in the single crystal Bi0.5Sb1.5Te3 which at room temperature is 2 - 5 nm (it is much smaller than the dimensions of CSR in the samples). The method for evaluation of L in polycrystalline samples is proposed. At room temperature, L is close to the mean free path in single crystals. Scattering parameter holes in SPS samples obtained from the temperature dependence of the Seebeck coefficient are within the measurement error equal to the parameter of the scattering of holes in a single crystal. The figure of merit ZT of SPS samples as a function of composition and sintering temperature has been investigated. Maximum ZT, equal to 1.05 at room temperature, is obtained for the composition Bi0.4Sb1.6Te3 at Ts = 500˚C and a pressure of 50 MPa. The causes of an apparent increase in thermoelectric efficiency are discussed.
1. Introduction
The last years have been characterized by the emergence of a large number of investigations of nanostructured thermoelectric materials, primarily on the basis of solid solutions (Bi, Sb)2Te3. Despite the lack of notable practical results received to date, the interest to work in this direction is not waning, because it indicates the way on which it is possible to get the long-awaited increase in thermoelectric efficiency ZT for various thermoelectric devices. The results received to date are values of ZT = 1.4 [1] to ZT = 1.8 [2].
Various aspects of the current state of work on the bulk nanostructured materials and their development prospects are contained in [3-6]. In most investigations, the nanostructured material is obtained by grinding in a planetary ball mill with the subsequent consolidation of nanopowders by hot pressing [4]. In some cases melt spinning is used [7,8], and then compacting is performed by spark plasma sintering method [8].
This work is largely devoted to experimental works on nanostructural material on the basis of (Bi, Sb)2Te3 held in Russia [9-16]. All of them began around the same time and used similar techniques as those in papers [1,2,17]. To create bulk nanocrystalline thermoelectric materials by mechanical activation process in a planetary ball mill with subsequent hot pressing was previously suggested in [13] for creating percolate structures based on fullerenes. The results obtained in subsequent research are partially shown in [14-16].
In the present work compacting bulk nanostructured materials on the basis of solid solutions (Bi, Sb)2Te3 are obtained by the spark plasma sintering method (SPS), which has a number of advantages over the traditional method of hot pressing [18]. All of the above mentioned works often do not contain information relating to obtaining samples, so the comparison of the properties presented in different works is somewhat difficult. In this paper an attempt of a systematic comparison of the structural and thermoelectric properties of nanostructured thermoelectric materials with their composition and the regime of obtaining them is made.
2. Preparation of Samples
Nanostructured samples were received from nanopowder of previously synthesized material of desired composition. For synthesis Bi (99.999), Sb (99.999), Te (99.999) were used. The synthesis was made by direct alloying the components in sealed quartz ampoules previously evacuated. The ingots were subjected to milling in protective atmosphere in the high-energy planetary ball mill AGO-2U-type (Russia) or Retsch PM400. Parallel to ingot milling powder source material was made by mechanochemical synthesis of original components. In using these methods no differences in the size and composition of nanoparticles, or thermoelectric prperties of bulk material were detected. SPS was made in the installation SPS-511S. Nanopowder billet previously received by cold pressing was placed in a graphite press mold. All nanopowder operations were performed in the glove box in protective atmosphere to control the moisture and O2. O2 concentration was maintained at a level below 10 ppm to prevent oxidation of the nanopowder. The disc shaped samples sintered in the graphite press mold had a thickness from 3 up to 10 mm and diameter of 20 mm. Sintering was conducted at temperatures from 250˚C to 550˚C under pressure from 30 to 70 MPa for 5 min. Samples of the desired size, depending on the method of measuring the properties were cut out from the discs by electro-erosive cutting machine ART-151 (Russia).
3. Structural Investigation
Structural researches of powders and sintered material were carried out by the X-ray method on diffractometer Bruker D8 with the use of CuKα of radiation. Morphology of the surface of a fracture of the sintered samples in secondary electrons was watched through the scanning electron microscope (SEM) of JSM-6480LV of JEOL firm. The research of the samples structure by a method of transmission electronic microscopy was carried out in electron microscope of JEM 2100 with high resolution of JEOL firm, the microscope can work both in a diffraction mode, and an image mode. The resolution of the microscope is at point 2.3 Å and in spectral line-1.4 Å (direct increase to 1.5 million times). The determination of the elemental composition in the local regions of the sample was determined by energy dispersive spectrometry method, the consoles INCA DRY COOL Company OXFORD Instruments being used. The properties of bulk nanostructured material are to a large extent dependent on those of the source powders. Powder particles were found to be single-phase and to have the composition of the source material. The average particle size determined according to transmission electron microscopy was 10 - 12 nm, which corresponds to the size of coherent scattering regions (CSR) defined by X-ray line broadening.
The powder is agglomerated. The agglomerate size depending on the milling conditions varies from 0.2 μm to several μm. The bright-field image of several powder agglomerates is shown in Figure 1(a). Figure 1(b) shows the diffraction pattern of the relevant area.
The broadened rings in the electron diffraction pattern indicate the finely dispersed structure of the agglomerates. Individual particles that make up the agglomerates are clearly visible on the dark-field image obtained in the

Figure 1. Bright-field (a) and dark-field (c) image of several powder agglomerates. Diffraction pattern corresponding to the agglomerate area (b), high resolution image of a single agglomerate particle in a transmission electron microscope (d).
reflexes, which can be seen on the ring diffraction pattern (Figure 1(c)). Figure 1(d) shows a high-resolution image of single agglomerate particle of ~12 nm size.
Saving the nanocrystalline state in compact samples is a major problem associated with the negative impact of recrystallization processes that lead to the enlargement of the grains. The microstructure of the samples sintered at high temperature is usually judged by the morphology of the fracture surface when observed in a scanning electron microscope. Figure 2 shows SEM images of the fracture surface for the samples obtained by SPS at different sintering temperatures  from 250˚C to 400˚C. At Ts = 350˚C and Ts = 400˚C the grains grow to the size of a few micrometers and acquire crystal faces, which indicates actively proceeding process of recrystallization. The samples annealed at lower temperatures have a highly dispersed structure, the fragments of the fracture surface are not faceted.
from 250˚C to 400˚C. At Ts = 350˚C and Ts = 400˚C the grains grow to the size of a few micrometers and acquire crystal faces, which indicates actively proceeding process of recrystallization. The samples annealed at lower temperatures have a highly dispersed structure, the fragments of the fracture surface are not faceted.
CSR was used as the main characteristic of the structure at the nanoscale size in the our papers (e.g. [14,19]). When the grain size is up to several tens of nanometers the CSR size coincides with the grains size, revealed in the image of the fracture surface of compact samples in a scanning electron microscope (as, for example, it was noted above for the nanopowder). CSR are part of the internal structure for larger grains. CSR dimensions are defined by grain fragmentation caused by different mechanisms related to various types of structural defects. The curves of the size distribution of CSR obtained by X-ray diffraction for samples at Bi0.4Sb1.6Te3 are in Figure 3 for Ts = 250˚C (1), Ts = 300˚C (2), Ts = 450˚C (3), Ts = 500˚C (4). The values along the y axis are the relative

Figure 2. SEM images of the fracture surface in secondary electrons for the samples obtained by the SPS method at Ts = 250˚C (a); Ts = 300˚C (b); Ts = 350˚C (c) and Ts = 400˚C (d).
volume of CSR in various sizes 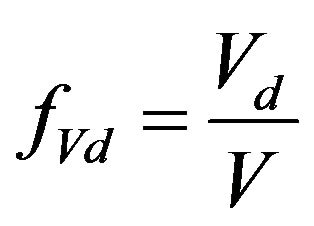 where
where 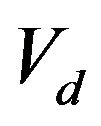
is CSR volume with size d, and 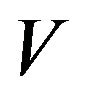 is the total volume of CSR. The accepted method of measurement can reliably determine the size of CSR only if d ≤ 300 nm. Therefore the distribution curves shown in Figure 3 are limited by this value. In the studied sintering temperature range CSR have maximum volume fraction in CSR size —from 50 to 200 nm.
is the total volume of CSR. The accepted method of measurement can reliably determine the size of CSR only if d ≤ 300 nm. Therefore the distribution curves shown in Figure 3 are limited by this value. In the studied sintering temperature range CSR have maximum volume fraction in CSR size —from 50 to 200 nm.
Figure 3 also shows that the volume fraction of CSR with d ≥ 150 increases when 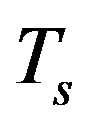 is increased from 250 to 300˚C. Simultaneously, the maximum in the distribution of CSR shifts to higher value of d. At
is increased from 250 to 300˚C. Simultaneously, the maximum in the distribution of CSR shifts to higher value of d. At  ˚C CSR size increased to such values that broadening of X-ray diffraction peaks is no longer observed. However, at higher
˚C CSR size increased to such values that broadening of X-ray diffraction peaks is no longer observed. However, at higher 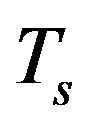 the volume fraction of CSR for d ≥ 150 nm decreases and the distribution of CSR in size moves to smaller values of CSR. As a result the values of CSR at Ts = 500˚C are significantly lower than that at Ts = 250˚C.
the volume fraction of CSR for d ≥ 150 nm decreases and the distribution of CSR in size moves to smaller values of CSR. As a result the values of CSR at Ts = 500˚C are significantly lower than that at Ts = 250˚C.
In [20] the distribution of the number of nanograins in the nanostructured sample Bi0.5Sb1.5Te3 is given. In order to proceed to the distribution of CSR on their quantity 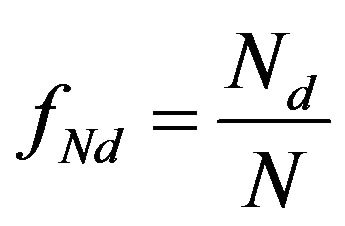 where
where —the number of CSR size dand N-the total number of CSR, it is necessary to divide the volume distribution into the volume of these regions, which is proportional to d3. Thus obtained distribution of CSR number is shown in Figure 4.
—the number of CSR size dand N-the total number of CSR, it is necessary to divide the volume distribution into the volume of these regions, which is proportional to d3. Thus obtained distribution of CSR number is shown in Figure 4.
The construction of Figure 4 was carried out on a logarithmic scale, because then the curves are symmetric with respect to the distribution maximum. The maximum number of CSR corresponds to the range of sizes from 20

Figure 3. The relationship between the volume fraction and the size of CSR in samples Bi0.4Sb1.6Te3, sintered at temperatures of 250˚C, 300˚C, 450˚C and 500˚C.
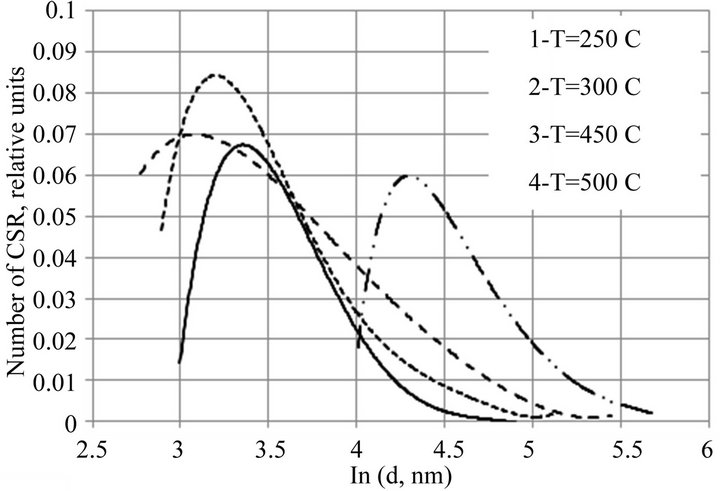
Figure 4. The relationship between the number of CSR and their size in the samples Bi0.4Sb1.6Te3, sintered at temperatures of 250˚C, 300˚C, 450˚C and 500˚C.
to 75 nm, the maximum on the distribution curves shifted to significantly smaller CSR compared to the maximum volume fraction. The displacement depends on the slope of 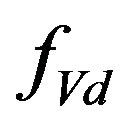 in the region before the maximum. When the slope is less, the displacement is greater. The symmetry of the curves in the logarithmic scale indicates that they can be satisfactorily described by a log-normal distribution in which the probability density of the number of CSR with the size of d is given by:
in the region before the maximum. When the slope is less, the displacement is greater. The symmetry of the curves in the logarithmic scale indicates that they can be satisfactorily described by a log-normal distribution in which the probability density of the number of CSR with the size of d is given by:
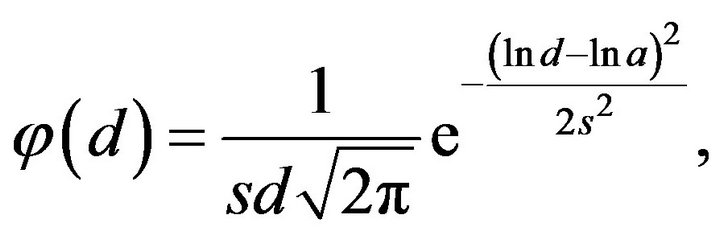 (1)
(1)
where a and s are parameters of the distribution. For a log-normal distribution a is the median, i.e. the number of grains with a size larger than a equals the number of grains with a size smaller than a. For the most interesting, in view of their nanostructure, samples obtained at 450˚C and 500˚C, the median value is 36 and 46 nm respectively. However, the total volume for the size of CSR, less than the median does not exceed a few percent. Recalculation of the number distribution of grain sizes [20] into their volume fraction shows that the volume fraction of nanograins with sizes less than 100 nm is very small and does not exceed 2% to 4%. Besides, our attention was drawn to a shift to the small size and, simultaneously, the broadening of the distribution 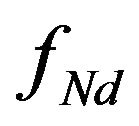 at the sintering temperature Ts = 450˚C versus Ts = 300˚C. This is certainly due to the grinding process of CSR and appearing of a large number of CSR of small size.
at the sintering temperature Ts = 450˚C versus Ts = 300˚C. This is certainly due to the grinding process of CSR and appearing of a large number of CSR of small size.
For a more complete picture of the structure of the samples, sintered at different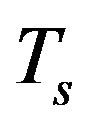 , the study was conducted by transmission electron microscopy. Even at
, the study was conducted by transmission electron microscopy. Even at 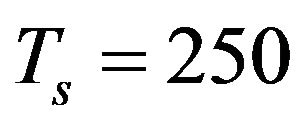 ˚C the grains are the size on the order more than the starting powder particles and continue to grow with increasing the sintering temperature to Ts = 400˚C. The samples sintered at temperatures from Ts = 250˚C to Ts = 350˚C show a significant difference in grain size, which practically disappears at the sintering temperature Ts = 400˚C. All this is the result of recrystallization, which is consistent with the increase of CSR, but which are still smaller than the size of the grains. At temperatures of Ts = 250˚C - 300˚C the fragmentation of some grains occurs due to dislocations. At Ts = 350˚C in the material structure there appear nanoparticles (Figures 5 (a) and (b)) the amount of which does not increase with increasing temperature. According to energy-dispersive X-ray spectroscopy analysis the composition of the nanoparticles does not differ from that of the surrounding grains. That is why it is possible to suggest that these nanoparticles are inherited from the original powder. In some grains, twinning occurs (Figure 5(c)). With increasing
˚C the grains are the size on the order more than the starting powder particles and continue to grow with increasing the sintering temperature to Ts = 400˚C. The samples sintered at temperatures from Ts = 250˚C to Ts = 350˚C show a significant difference in grain size, which practically disappears at the sintering temperature Ts = 400˚C. All this is the result of recrystallization, which is consistent with the increase of CSR, but which are still smaller than the size of the grains. At temperatures of Ts = 250˚C - 300˚C the fragmentation of some grains occurs due to dislocations. At Ts = 350˚C in the material structure there appear nanoparticles (Figures 5 (a) and (b)) the amount of which does not increase with increasing temperature. According to energy-dispersive X-ray spectroscopy analysis the composition of the nanoparticles does not differ from that of the surrounding grains. That is why it is possible to suggest that these nanoparticles are inherited from the original powder. In some grains, twinning occurs (Figure 5(c)). With increasing  the quantity of grain junctions approaching the equilibrium angle of 120 degrees (Figure 5(d)) grows. According to transmission electron microscopy the samples sintered at Ts = 400˚C have a more perfect internal structure of the grains, which is consistent with the sharp increase in the size of the CSR.
the quantity of grain junctions approaching the equilibrium angle of 120 degrees (Figure 5(d)) grows. According to transmission electron microscopy the samples sintered at Ts = 400˚C have a more perfect internal structure of the grains, which is consistent with the sharp increase in the size of the CSR.
At Ts = 450˚C, the images of transmission electron microscopy are changed dramatically. A large amount of nanosized grains, located both inside and on the grain boundaries (Figure 6(a)) appear. The total volume of new nanograins is not great. The distribution curve of volume fraction of CSR in sizes (Figure 3) shows an increase in the relative fraction of CSR with d < 100 nm and a decrease in the fraction of CSR with the size of d > 200


Figure 5. Bright-field images of the structure of the thermoelectric material Bi0.4Sb1.6Te3, obtained by SPS method at sintering temperatures Ts = 250˚C - 400˚C: (a) Nanoparticles in the grains of the sample (Ts = 250˚C - 350˚C); (b) A high-resolution nanoparticles on the boundary between two grains; (c) A grain with a twin crystals; (d) The junction of three grains (Ts = 400˚C).

Figure 6. Bright-field images of the structure of the thermoelectric material Bi0.4Sb1.6Te3, obtained by SPS method at 450˚C: (a) Nanoparticles in the sample grains; (b) The high-resolution image of nanoparticles in the volume of the grain; (c) The high-resolution image of nanoparticles at the junction of three grains; (d) The comparison of the composition of the solid solution in the nanoparticle and the surrounding grain, defined by local energy-dispersive X-ray spectroscopy.
nm. The decrease of CSR occurs at very low micro strains. with confidence that the emergence of nanograins is due to secondary recrystallization. Thus, the grain growth in the recrystallization process imposes itself on the secondary recrystallization process, which actively takes place at temperatures above Ts = 450˚C.
At 500˚C, the amount of new nanoparticles increases Figure 6(b) shows the images of nanoscale grains at high resolution in the volume and on the border with large grains (Figure 6(c)). The results of energy dispersive X-ray spectroscopy (Figure 6(d)) indicate that the composition of nanosized grains is not different from that of the sample as a whole. So it is possible to conclude substantially, they increase in size and have a good faceting (Figure 7). So the grains of different size are observed in the volume of the “old” grains: a newly originated nucleus and the grains which had time to grow up at a later stage of recrystallization. In some cases, the newly grown small grains occupy the entire volume of the “old” grain. In the structure of sintered at 500˚C samples there appear pores. The formation and subsequent growth of nanograins during secondary recrystallization lead to the fragmentation of the “old” grain and result in the reduction of the CSR size.
The driving force of the formation of small grains at the secondary recrystallization may be accounted for by

Figure 7. Bright-field images (a), (b) of the structure of Bi0.4Sb1.6Te3, sintered at a temperature of 500˚C.
reducing both of energy in the grains boundaries and bulk energy of the grains. Solid solutions of bismuth antimony telluride in their physical properties are strongly anisotropic materials. They are characterized by a strong anisotropy of crystal growth in different directions [22]. The grain boundaries energy is also highly dependent on the orientation of the boundary. In recrystallization the grains grow preferentially in the direction of the greatest rate of growth, and thus formed boundaries between the grains have a random orientation which does not correspond to the borders with minimum energy. Therefore at some temperatures “new” grains of the same composition can be generated, their boundaries have a lower energy than that of the “old” grain boundaries. Consequently, despite the fact that the total length of the border increases, their total energy can be reduced.
Another possibility is to reduce the energy associated with intrinsic defects. In the absence of dislocations the latter can be intrinsic point defects (IPD) arising in the process of samples preparation. In this case, we can assume that the emerging new grains have a lower concentration of IPD compared to that of the “old” grain. The high concentration of IPD in the bulk material may be caused by their appearance in the source powder particles as a result of grinding in a high-energy ball milling. In this case, for the implementation of recrystallization process an inhomogeneous density distribution of IPD in nanoscale level is required. The emergence of such local inhomogeneity in the SPS samples can have various technological reasons related to both the process of milling and the peculiarities of their sintering. The reduction of the grains volume concentration of IPD occurs in the process of secondary recrystallization. As this process is caused by atom diffusion, the secondary recrystallization is active at high sintering temperatures in the conditions of the increased mobility of IPD. Excess of IPD can both go to the grain boundaries and form clusters in the bulk of the grains. The pores in the structure of the samples sintered at Ts = 450˚C - 500˚C observed in the electron microscope indicate that the IPD have vacancy nature.
The formation of donor defects in materials obtained by extrusion of the thermoelectric material Bi0.5Sb1.5Te3 is well known [22]. The value of the thermoelectric power in such materials is much larger than in crystalline materials of the same composition. Electrical data presented below in the section “Thermoelectric Properties”, indicate similar processes for SPS. In the SPS samples sintered at temperatures Ts = 250˚C - 350˚C, the Seebeck coefficient is larger and conductivity is less than the corresponding values in single crystal samples of the same composition. At elevated SPS temperatures there appears a simultaneous increase in the electrical conductivity and a decrease of the Seebeck coefficient, which shows an increase in the concentration of holes. Therefore, we can assume that the secondary recrystallization causes reduction of IPD donor type in grain volume.
The combination of these results suggests that the main type of defects in the bulk grains are donating IPD vacancy type, which are likely to be not isolated, but presented in the form of nanoscale associations. Perhaps these associations are centers of origin of new nanograins. It is possible to assume a scheme for the formation of IPD. Rhombohedral lattice Bi2Te3 consists of layers Te(1)-BiTe(2)-Bi-Te(1) perpendicular to the threefold axis [21]. The formation of vacancies  can easily take place in any mechanical treatment because of the weak van der Waals bonds between the layers of Te(1)-Te(1). Formed in the process free Te atoms can be located between the same layers because of a large distance between them. These vacancies can be filled with Bi atoms due to the small difference in electronegativity between Bi and Te. As a result there appear anti-site defects
can easily take place in any mechanical treatment because of the weak van der Waals bonds between the layers of Te(1)-Te(1). Formed in the process free Te atoms can be located between the same layers because of a large distance between them. These vacancies can be filled with Bi atoms due to the small difference in electronegativity between Bi and Te. As a result there appear anti-site defects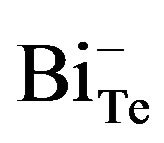 , which is accompanied by the formation of vacancies
, which is accompanied by the formation of vacancies 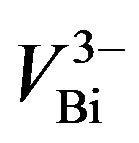 in cationic sublattice. In [23] the following scheme of interaction between vacancies and anti-site defects
in cationic sublattice. In [23] the following scheme of interaction between vacancies and anti-site defects 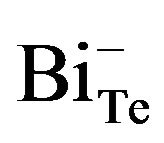 is suggested:
is suggested:
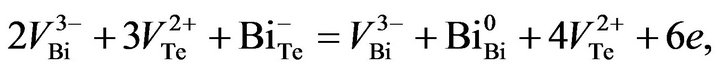 (2)
(2)
where e—an electron charge. As a result in the p-type material carrier concentration in the cold-pressed billet reduces and after subsequent sintering it increases due to annealing of the donor defects.
4. Determination of the Mean Free Path of the Holes in a Single Crystal Bi0.5Sb1.5Te3
The most common considerations tell us that the scattering of charge carriers at the grain boundaries will significantly affect the kinetic effects only when the grain size is comparable to the mean free path of the charge carrier. Therefore the determination of the mean free path in the polycrystalline material plays a main role in understanding how large nanostructures (grains, CSR) should be to influence the properties of polycrystalline materials.
In anisotropic crystals the relationship between the electric current density j and the electric field E and a weak magnetic field H is given by [21]
 (3)
(3)
where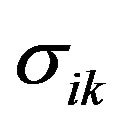 —components of the conductivity tensor of the second rank,
—components of the conductivity tensor of the second rank,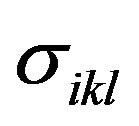 —third-rank tensor, repeated indices being summed. For lattice symmetry of solid solutions Bi2Te3-Sb2Te3 tensors
—third-rank tensor, repeated indices being summed. For lattice symmetry of solid solutions Bi2Te3-Sb2Te3 tensors 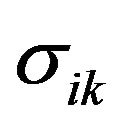 and
and  have only two independent components. If we choose the coordinate axes so that zy plane coincides with one of the three planes of the crystal symmetry, the direction of x-axis coincides with the twofold axis direction, and the direction of z axis coincides with the direction of the threefold axis [24], then tensor
have only two independent components. If we choose the coordinate axes so that zy plane coincides with one of the three planes of the crystal symmetry, the direction of x-axis coincides with the twofold axis direction, and the direction of z axis coincides with the direction of the threefold axis [24], then tensor 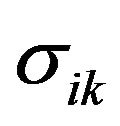 is diagonal and it is only components in the plane perpendicular to the threefold axis
is diagonal and it is only components in the plane perpendicular to the threefold axis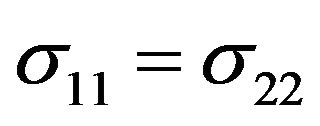 , and in the direction parallel to the threefold axis
, and in the direction parallel to the threefold axis 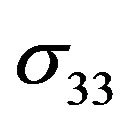 that are non-zero. Tensor
that are non-zero. Tensor 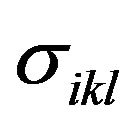 has nonzero components:
has nonzero components:
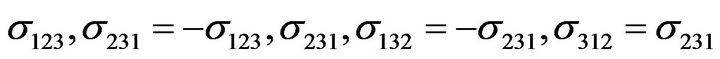
Expressions for the components of these tensors can be found in [21], the transition from the notation [24] to the notation of [21] being carried out by the index changes .
.
The definition of the independent tensor components  and
and 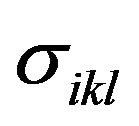 requires two independent measurements for different orientations of the current directions and electric field. However, the approximation of isotropic scattering and knowledge of the parameters of the band structure allows us to use only one measurement. Within six-ellipsoidal model [25] the components of the electrical conductivity can be expressed as
requires two independent measurements for different orientations of the current directions and electric field. However, the approximation of isotropic scattering and knowledge of the parameters of the band structure allows us to use only one measurement. Within six-ellipsoidal model [25] the components of the electrical conductivity can be expressed as
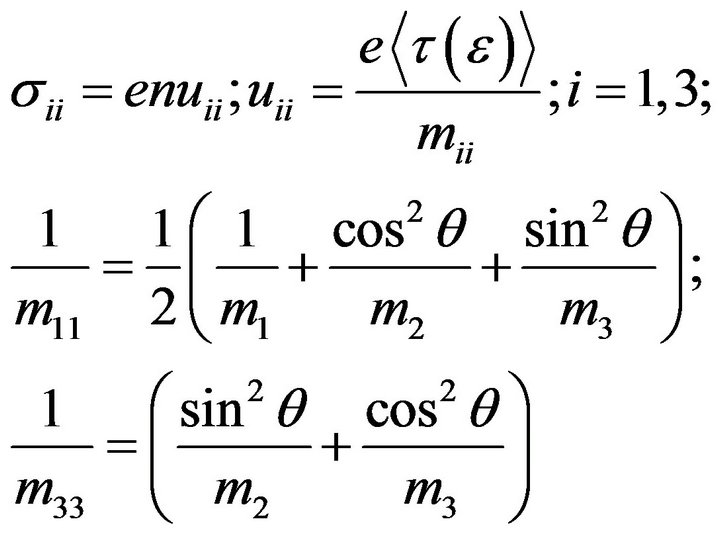 (4)
(4)
where —the charge of the electron,
—the charge of the electron,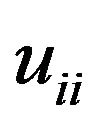 —mobility for the particular direction ii,
—mobility for the particular direction ii, —the concentration of charge carriers
—the concentration of charge carriers —effective masses , corresponding to the three axes of the ellipsoid of constant energy,
—effective masses , corresponding to the three axes of the ellipsoid of constant energy,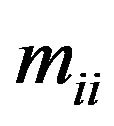 — the effective masses of conduction for the particular direction ii,
— the effective masses of conduction for the particular direction ii, —the angle of rotation of the ellipsoid in the reflection plane about the axis y,
—the angle of rotation of the ellipsoid in the reflection plane about the axis y,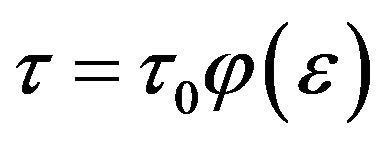 —relaxation time,
—relaxation time, —averaged over the energy relaxation time. Averaging function
—averaged over the energy relaxation time. Averaging function 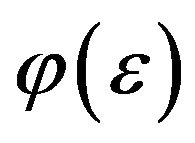 is the following
is the following
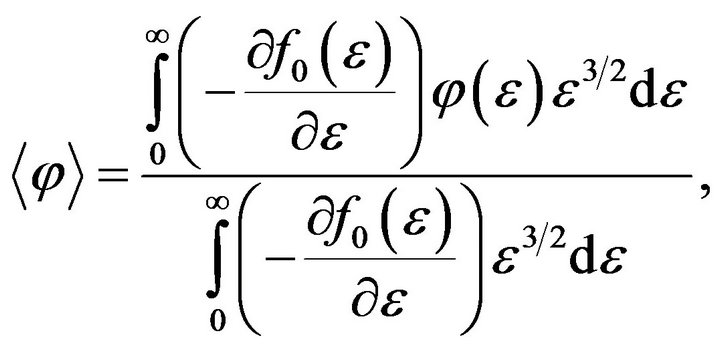 (5)
(5)
where  is the Fermi function.
is the Fermi function.
Components 123 and 231 of tensor 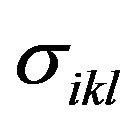 are
are
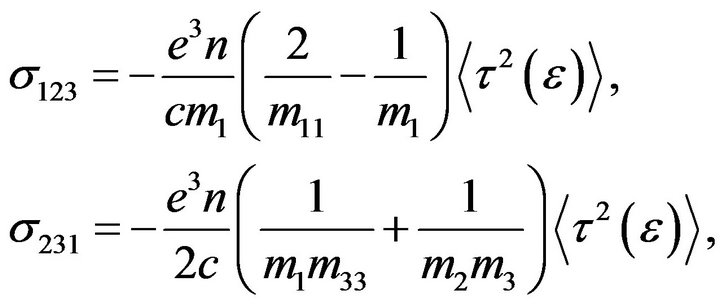 (6)
(6)
where c—light speed.
The connection between  and the concentration of charge carriers is given by
and the concentration of charge carriers is given by
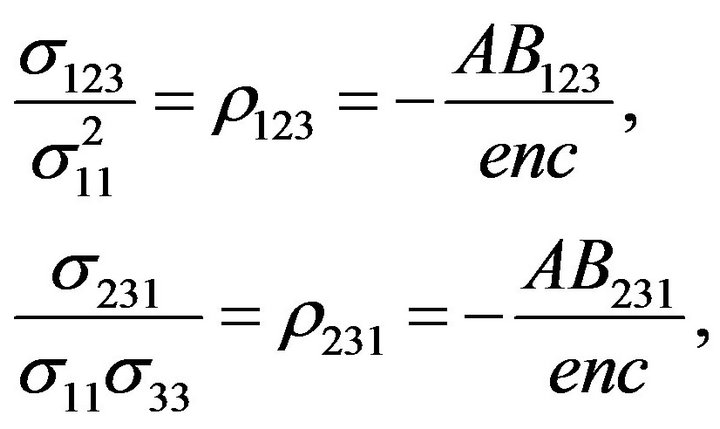 (7)
(7)
where 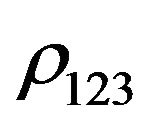 and
and 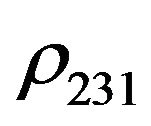 -corresponding Hall coefficients,
-corresponding Hall coefficients, –the Hall factor,
–the Hall factor, 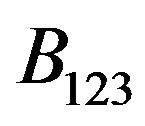 and
and 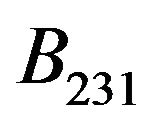 -anisotropy factors.
-anisotropy factors.
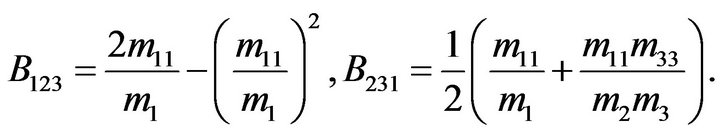 (8)
(8)
The Hall factor is expressed in the usual way
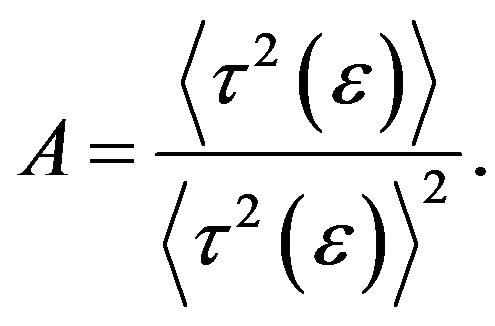 (9)
(9)
The concentration of charge carriers is
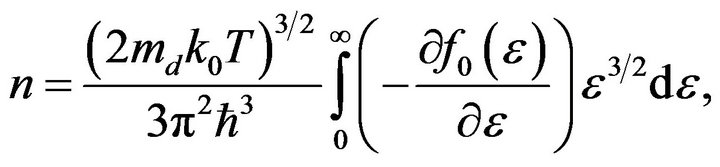 (10)
(10)
where —the effective mass of density of states,
—the effective mass of density of states,
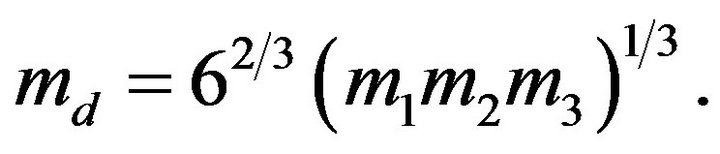 Equations (4)-(10) allow, for known model parameters [25], to calculate all the tensor components
Equations (4)-(10) allow, for known model parameters [25], to calculate all the tensor components  and
and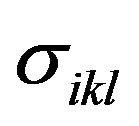 , the data on the electrical conductivity and the Hall coefficient measured for one direction being used.
, the data on the electrical conductivity and the Hall coefficient measured for one direction being used.
Effective masses used in the calculations are shown in Table 1.
The data in Table 1 show that it is possible to consider, with sufficient accuracy, the anisotropy factors  to be equal to 0.8.
to be equal to 0.8.
The mean free path for momentum in the direction ii—
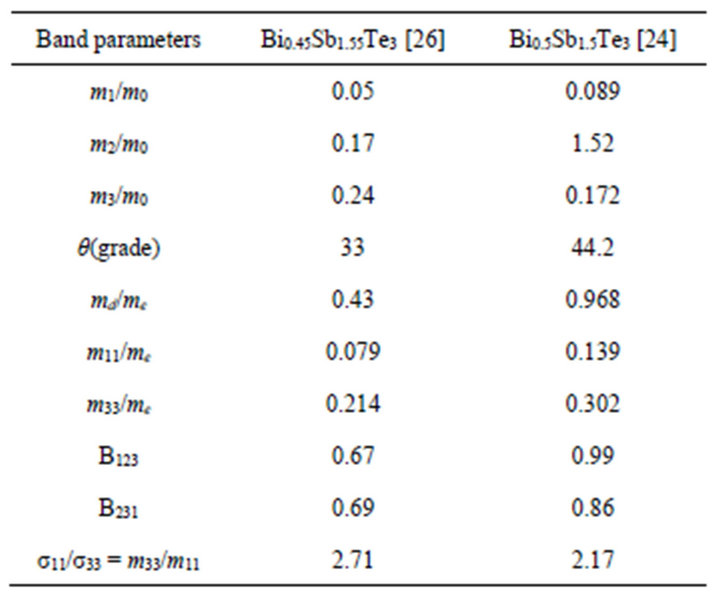
Table 1. The band parameters used in the calculation of the transport properties of the solid solution of antimony and bismuth telluride.
 can be defined as an average distance passed by a charge carrier during relaxation time for momentum. It can be approximately assumed that
can be defined as an average distance passed by a charge carrier during relaxation time for momentum. It can be approximately assumed that 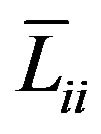 is the distance traveled at an average speed during average relaxation time. Both approaches are equivalent under degeneration.
is the distance traveled at an average speed during average relaxation time. Both approaches are equivalent under degeneration.
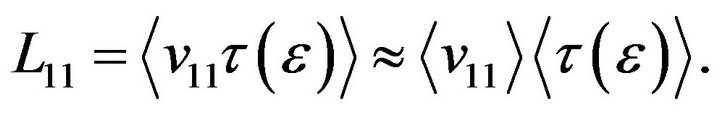 (11)
(11)
The average relaxation time can be found from the mobility (4). To find the average speed in six ellipsoid model [21] it is necessary to average quasi-momentum for the direction parallel to the threefold axis, and for the direction parallel to cleavage planes. It is sufficient to perform averaging for one ellipsoid, because for the rest of them, the results are equivalent. The expression for the mean velocity in this case can be represented as:
 (12)
(12)
where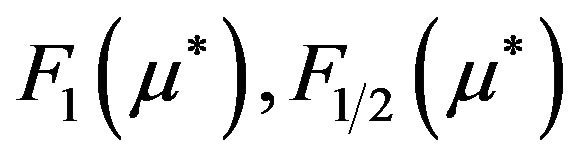 —appropriate Fermi integrals—
—appropriate Fermi integrals—
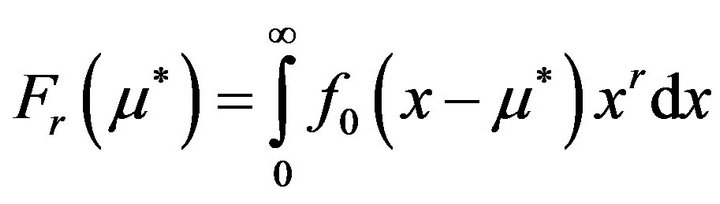 , and
, and —the reduced Fermi level, and
—the reduced Fermi level, and  are
are
 (13)
(13)
and
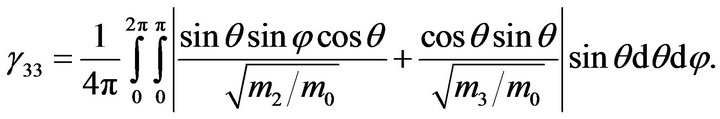 (14)
(14)
The speed that is close to the maximum, in the degenerate case can be found from
 (15)
(15)
Expression (15) is convenient for estimating the upper limit of the mean free path. At room temperature it overestimates the value of the mean free path, calculated from Equations (12)-(14) by about 50% - 80%, but that is not critical to this consideration. Figure 8 shows the temperature dependence of the electrical conductivity and the Hall coefficient for single crystal Bi0.5Sb1.5Te3 [27].
Figure 8 shows the drop in conductivity with increasing temperature from 10 K to room temperature, which is associated with the fall of the mobility and the growth of the Hall coefficient, due to the removal of degeneracy and the growth of the Hall factor A. Considering that all the impurities are ionized, and the Hall factor for degeneracy is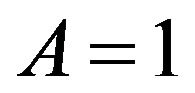 , the carrier concentration in the sample is 3.3 × 1019 cm−3.
, the carrier concentration in the sample is 3.3 × 1019 cm−3.
Dependence of the mobility 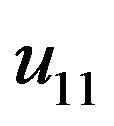 on temperature is shown in Figure 9.
on temperature is shown in Figure 9.
The calculation of the temperature dependence of the mean free path by the Formulas (11)-(14) is shown in Figure 10. Figure 10 shows that the mean free path

Figure 8. Temperature dependence of the electrical conductivity 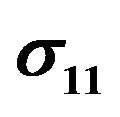 and the Hall coefficient
and the Hall coefficient 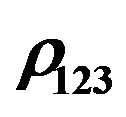 at low temperatures for a single-crystal sample Bi0.5Sb1.5Te3.
at low temperatures for a single-crystal sample Bi0.5Sb1.5Te3.
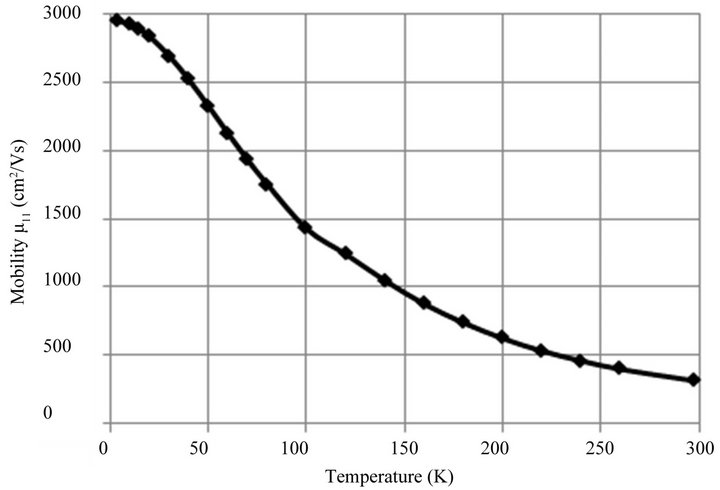
Figure 9. The dependence of the mobility 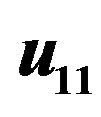 in the single crystal Bi0.5Sb1.5Te3 on the temperature.
in the single crystal Bi0.5Sb1.5Te3 on the temperature.
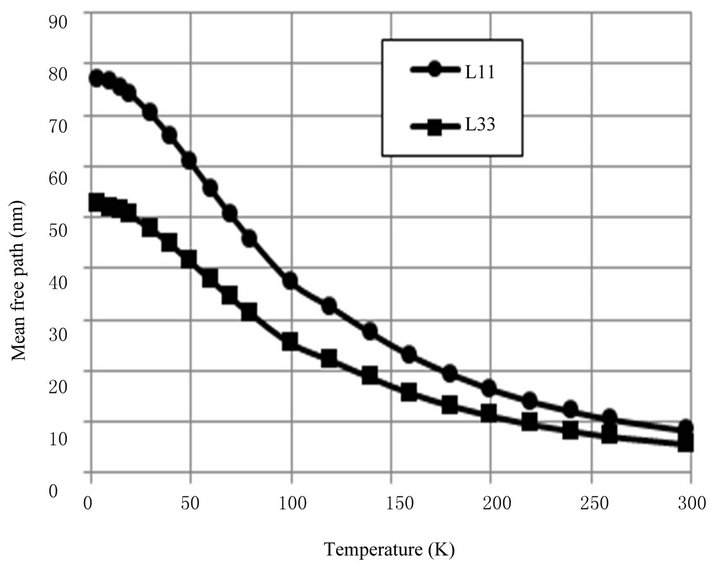
Figure 10. The dependence of the mean free paths in the single crystal Bi0.5Sb1,5Te3 on temperature.
for momentum in Bi0.5Sb1.5Te3 at room temperature is less than 5 nm, and the condition of the influence of scattering at grain boundaries on the kinetic effects in nanostructured samples antimony telluride requires the size of the individual grains or CSR of such an order. Thus, one can say with certainty that the nanostructured samples, obtained by the SPS method or by hot pressing [1] do not satisfy the condition of the proximity values of the grain sizes (or CSR) and the mean free path of charge carriers for momentum. Therefore, the scattering of charge carriers on the grain boundaries can hardly play a significant role in the transport process in such materials.
5. Determination of the Mean Free Path of the Holes in the Nanostructured Bi0.5Sb1.5Te3
We assume that polycrystalline SPS material is generally isotropic, neglecting the small texture observed in [36]. However, individual grains that make up the polycrystalline material are anisotropic. We assume that the properties of the individual grains can be described on the basis of the results obtained for single crystals, and therefore to estimate the electrical properties of the grains we can use the theoretical concepts of their properties, as to measure electrical properties of individual grains in a compact polycrystalline material is a completely impossible task.
The transition from the electrical properties of the grains to the electrical properties of isotropic polycrystalline material is carried out in the effective medium model [21,28,29]. It is used to calculate the electrical parameters of the polycrystalline material consisting of anisotropic grains with known properties. In our case it is necessary to solve the inverse problem: to restore the properties of the grains using the known properties of the isotropic polycrystalline sample, on the base of the results obtained from the study of electrical properties of single crystals [27].
The weak point of the effective medium model is the neglect of the processes at the grain boundaries. This assumption is valid if the characteristic dimensions, which can be represented by the mean free path of the holes, are much smaller than the size of the grains. The evaluation of the free path of the holes, held in the previous section, confirms the validity of this approach.
The relation between the electrical conductivity of the polycrystal in the effective medium model and electrical conductivity tensor components in a single crystal is given by [28,21]
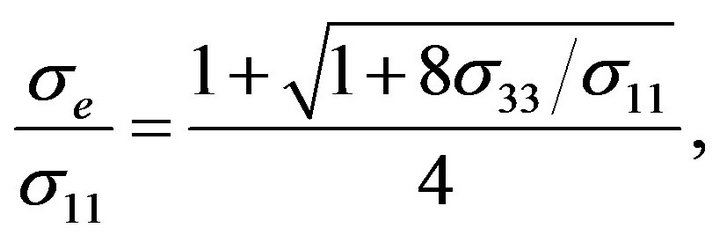 (16)
(16)
where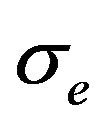 —the electrical conductivity of the polycrystal. Thus, using the data in Table 1, it is possible to get both components of the electrical conductivity tensor of individual crystal grains by measuring the electrical conductivity of polycrystalline. If we assume that the ratio
—the electrical conductivity of the polycrystal. Thus, using the data in Table 1, it is possible to get both components of the electrical conductivity tensor of individual crystal grains by measuring the electrical conductivity of polycrystalline. If we assume that the ratio 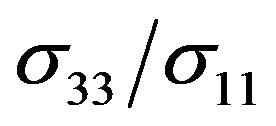 does not depend on the grain size, the expression (16) is valid regardless of the fractional composition of the grains forming the polycrystal.
does not depend on the grain size, the expression (16) is valid regardless of the fractional composition of the grains forming the polycrystal.
The relationship between the effective value 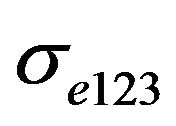 in a polycrystalline sample and the third-order tensors
in a polycrystalline sample and the third-order tensors 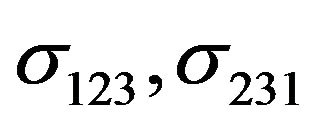 in a single crystal, in the effective medium approximation, is given in [30]
in a single crystal, in the effective medium approximation, is given in [30]
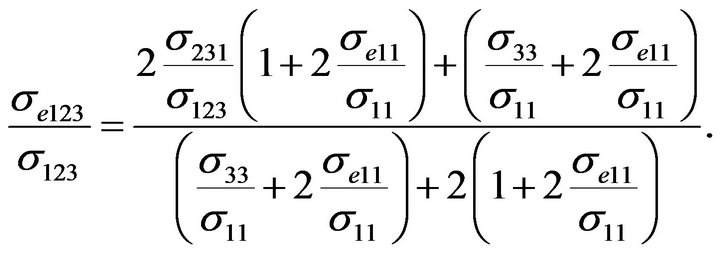 (17)
(17)
For the Hall coefficient in the isotropic polycrystal we have
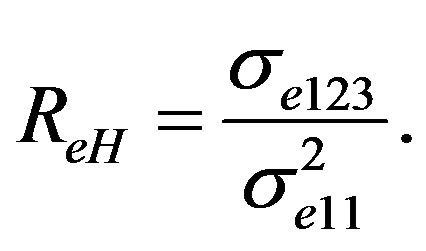 (18)
(18)
From Equations (7)-(11) we obtain
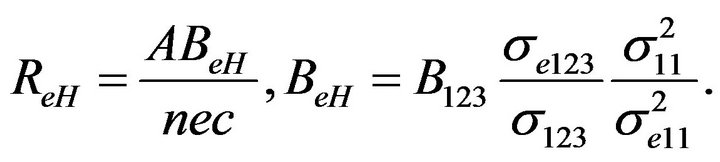 (19)
(19)
Thus, with the help of Equations (16)-(19) and the data on the effective mass (Table 1) it is possible to find the concentration of holes in polycrystalline solid solutions of antimony and bismuth telluride using the measurements of electrical conductivity and the Hall effect. The relations between the parameters of the polycrystal and those of a single crystal in the effective medium approach are given in Table 2.
Table 2 shows that, in spite of the fact that the effecttive masses in own axes of the ellipsoids, obtained by different authors [24,26], are quite noticeably different,
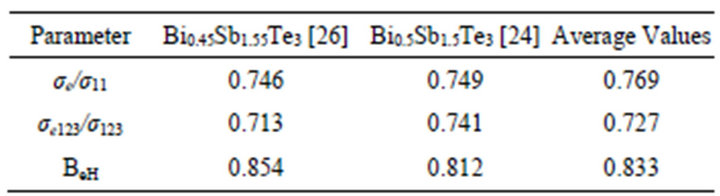
Table 2. The relationship between the single crystal parameters and the parameters of the polycrystal.
values necessary to us in a polycrystalline sample do not differ much. Therefore, to find properties of the individual single crystal grains forming a poly crystal from the properties of polycrystalline sample we can use the obtained average values of Table 2. After calculation of the components of the conductivity tensor and the carrier concentration in individual grains, we can proceed to the determination of the mean free path in individual grains.
We define the effective mobility in polycrystalline samples as
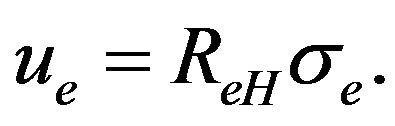 (20)
(20)
It is determined by measuring the electrical conductiveity and the Hall effect in polycrystalline samples. From Equations (16)-(19) it follows that
 (21)
(21)
Using Equation (21) we can calculate the values of mobility and the mean free path in individual grains [27] in a polycrystalline sample just as it was done for single crystals.
The results of the calculation of the mean free paths for polycrystalline nanostructured samples obtained by SPS method are shown in Figures 11 and 12. The reduction of the mean free path when Ts decreases cannot be attributed only to the reduction of the contact area between the grains, as this should not lead to a change in the temperature dependence . It can be seen from the Figures 11 and 12 that the values
. It can be seen from the Figures 11 and 12 that the values  and
and 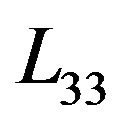 for the SPS polycrystalline samples at room temperature are on the order of several nanometers. So near to room temperature the size of CSR is one or two orders of magnitude larger than the mean free path of the holes in the grains. Thus it is possible to conclude that the scattering processes that decrease
for the SPS polycrystalline samples at room temperature are on the order of several nanometers. So near to room temperature the size of CSR is one or two orders of magnitude larger than the mean free path of the holes in the grains. Thus it is possible to conclude that the scattering processes that decrease 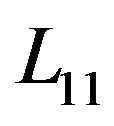 and
and 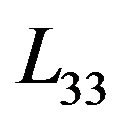 in the samples can be associated mainly with defects within the grains, i.e. with IPD, presence of which follows from the structural studies described earlier. This is especially true for the samples, which were obtained at low sintering temperatures (240˚C - 260˚C). Reduction of the concentration of IPD at the increase of
in the samples can be associated mainly with defects within the grains, i.e. with IPD, presence of which follows from the structural studies described earlier. This is especially true for the samples, which were obtained at low sintering temperatures (240˚C - 260˚C). Reduction of the concentration of IPD at the increase of 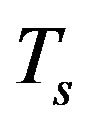 must be accompanied by an increase in mobility and, as a consequence, in the mean free path of holes, which is clearly seen from the Figures 11 and 12.
must be accompanied by an increase in mobility and, as a consequence, in the mean free path of holes, which is clearly seen from the Figures 11 and 12.
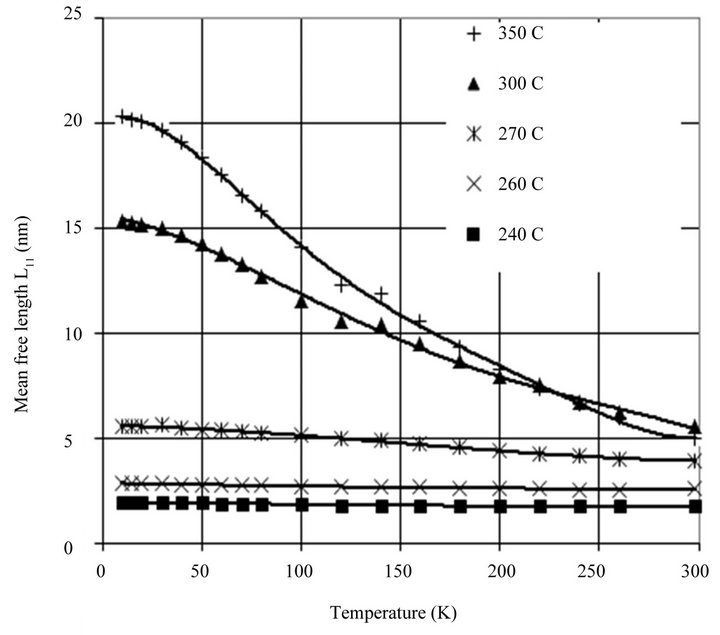
Figure 11. The dependence of the mean free path of holes in individual grains along cleavage planes L11 in SPS samples Bi0.5Sb1.5Te3. The sintering temperatures are shown in the figure.
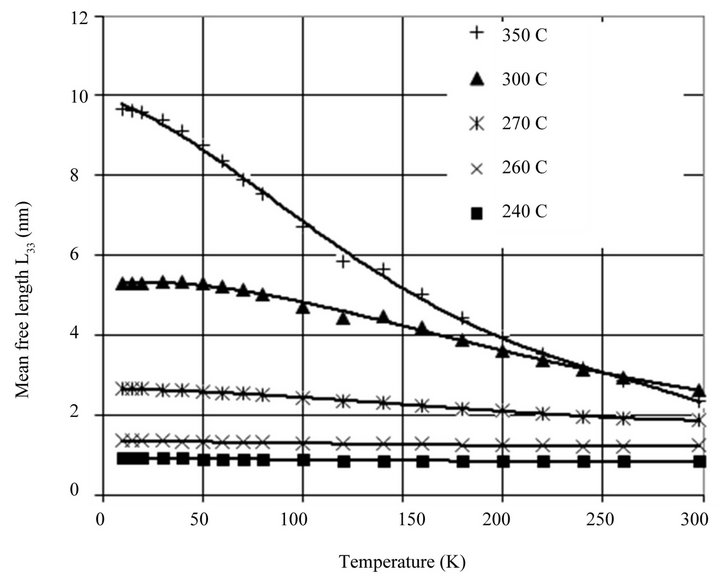
Figure 12. The dependence of the mean free path of holes in individual grains along the threefold axis L33 in SPS samples Bi0.5Sb1.5Te3. The sintering temperatures are shown in the figure.
As the temperature decreases due to the increase of the holes mean free path the difference between the latter and the value of CSR is less dramatic, and at low temperatures the effect of grain boundaries on the scattering mechanisms of holes can be permitted.
Thus, the results of the investigation of the holes mean free paths are in good agreement with the model, resulting from structural studies of SPS samples.
Figures 11 and 12 show that at low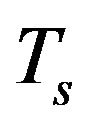 , the mean free path of the holes is very small, so the study of the Seebeck coefficient can restrict temperatures to Ts = 300˚C and Ts = 350˚C and compare the received data to those for a single crystal. Figure 13 shows the temperature dependence of the Seebeck coefficient for the SPS samples [31] and for a single crystal.
, the mean free path of the holes is very small, so the study of the Seebeck coefficient can restrict temperatures to Ts = 300˚C and Ts = 350˚C and compare the received data to those for a single crystal. Figure 13 shows the temperature dependence of the Seebeck coefficient for the SPS samples [31] and for a single crystal.
Figure 13 shows that the slopes of the curves for SPS samples and a single crystal are very close, so any radical changes in the scattering parameters 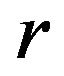 cannot be expected. The scattering parameter is found by solving the equation
cannot be expected. The scattering parameter is found by solving the equation
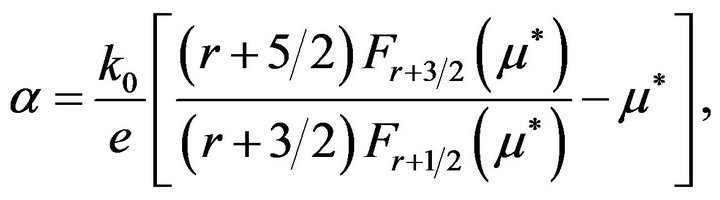 (22)
(22)
where 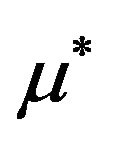 is the reduced Fermi level given by (10) and
is the reduced Fermi level given by (10) and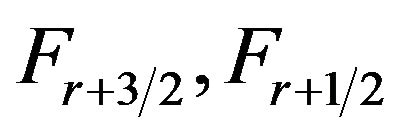 —Fermi integrals. The results of the calculation of the scattering parameter r are shown in Figure 14 [31]. Figure 14 shows that the scattering parameter r forthe samples obtained by SPS method at Ts = 350˚C and Ts = 300˚C is in good agreement with the scattering parameters for a single crystal and is equal to −0.75 ± 0.03, so it is difficult to expect any radical changes in the values of the Seebeck coefficient of SPS
—Fermi integrals. The results of the calculation of the scattering parameter r are shown in Figure 14 [31]. Figure 14 shows that the scattering parameter r forthe samples obtained by SPS method at Ts = 350˚C and Ts = 300˚C is in good agreement with the scattering parameters for a single crystal and is equal to −0.75 ± 0.03, so it is difficult to expect any radical changes in the values of the Seebeck coefficient of SPS
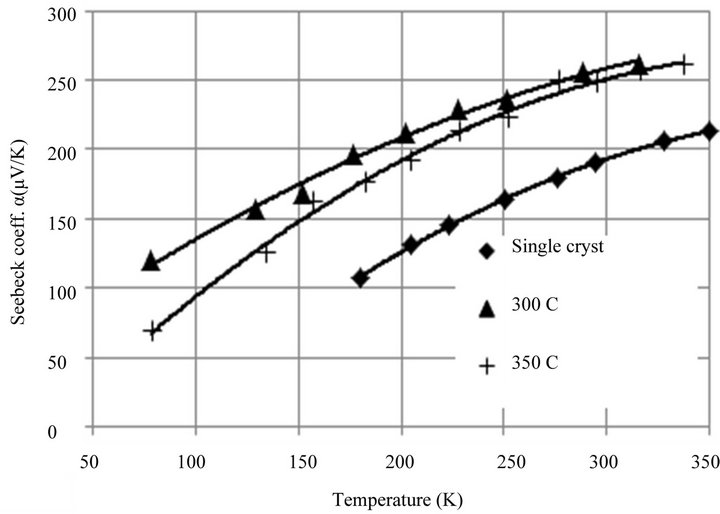
Figure 13. The temperature dependence of the Seebeck coefficient for SPS samples and for a single crystal.
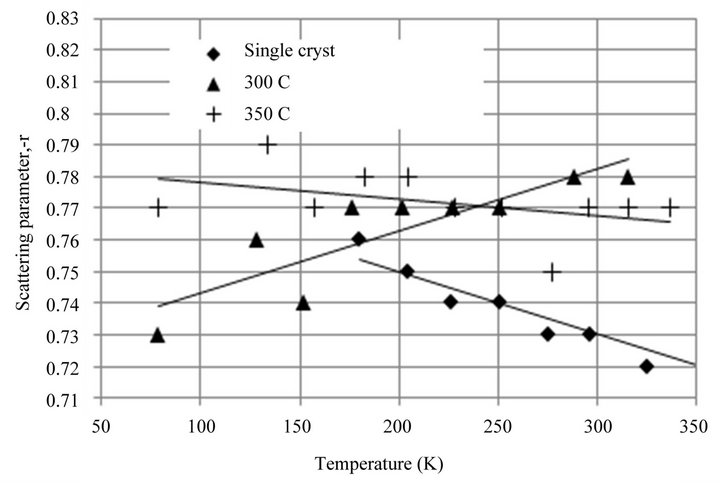
Figure 14. The dependence of the scattering parameter r on the temperature for the SPS samples and a single crystal. The sintering temperatures are shown in the figure.
samples compared to the Seebeck coefficient in a single crystalline samples with the same concentration of charge carriers. The difference of this scattering parameter from the acoustic dissipation parameter 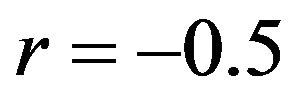 observed in Bi2-xSbxTe3 [26] and explained by influence of the heavy zone for high hole concentration.
observed in Bi2-xSbxTe3 [26] and explained by influence of the heavy zone for high hole concentration.
6. Thermoelectric Properties
Before discussing the results of the measurements of thermoelectric properties, the criteria for confidence to the results of measurements of these properties must be specified. Back in the 60s last century, it became clear that the separate measurement of thermoelectric parameters leads to a very high error in the measurement of figure of merit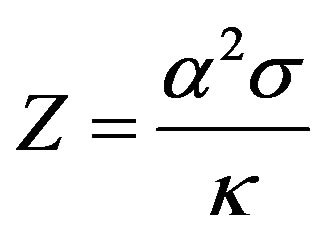 , where α—the Seebeck coefficient, σ electrical conductivity, κ-thermal conductivity. When the standard mean error of the measurements of individual parameters is about 5% then the average measurement error
, where α—the Seebeck coefficient, σ electrical conductivity, κ-thermal conductivity. When the standard mean error of the measurements of individual parameters is about 5% then the average measurement error  is at 20%. For measuring
is at 20%. For measuring  a technique has been developed [32], which allows to measure all these parameters on a single sample in a single measurement cycle, with the same temperature differences for
a technique has been developed [32], which allows to measure all these parameters on a single sample in a single measurement cycle, with the same temperature differences for  and
and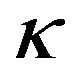 , and the same geometry for
, and the same geometry for  and
and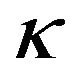 . The total accuracy of this method is about 10%. Its disadvantage is that it is necessary to have relatively large samples with a characteristic size of about 10 mm. The most universal method of measuring Z is that of Harman [33]. This method allows to determine
. The total accuracy of this method is about 10%. Its disadvantage is that it is necessary to have relatively large samples with a characteristic size of about 10 mm. The most universal method of measuring Z is that of Harman [33]. This method allows to determine  from the voltage drop across the sample at a constant and alternating current
from the voltage drop across the sample at a constant and alternating current 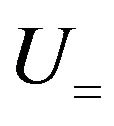 and
and , respectively. In this case,
, respectively. In this case, 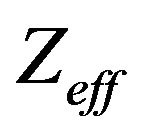 turns out to be
turns out to be
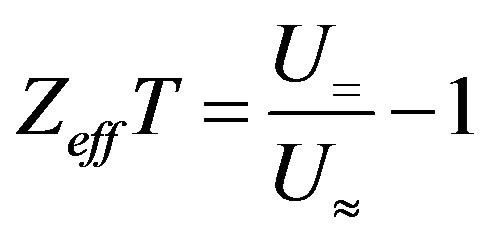 . The value of
. The value of 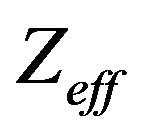 at room temperature is 5% - 12% less than Z. The simulation of heat loss [34,35] can significantly reduce this discrepancy, and then the total error is less than 5%. This method allows to measure figure of merit of the samples with the characteristic dimensions of about one mm. Its disadvantage is that the results somewhat distort contact resistances. Therefore, we can assume that only the data of
at room temperature is 5% - 12% less than Z. The simulation of heat loss [34,35] can significantly reduce this discrepancy, and then the total error is less than 5%. This method allows to measure figure of merit of the samples with the characteristic dimensions of about one mm. Its disadvantage is that the results somewhat distort contact resistances. Therefore, we can assume that only the data of  received by using one of the two methods are credible.
received by using one of the two methods are credible.
The above mentioned methods automatically provide the measurement of the thermal and the electrical conductivity of samples in one direction. The failure to do this can also lead to significant discrepancies in the results of the measurements of , as was shown in [36].
, as was shown in [36].
The measurement of the thermoelectric properties of bulk nanostructured materials (Bi, Sb)2Te3 at room temperature were determined by the Harman method on samples of size 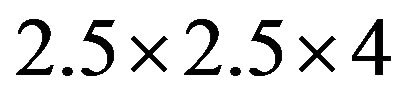 mm3. The characteristic feature of this method is that the thermoelectric figure of merit
mm3. The characteristic feature of this method is that the thermoelectric figure of merit , as α and σ, is determined directly from the experiment, and the thermal conductivity κ is calculated by the formula
, as α and σ, is determined directly from the experiment, and the thermal conductivity κ is calculated by the formula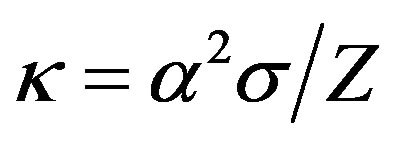 . In this case, electrical and thermal conductivity was determined for the same sample in the same direction.
. In this case, electrical and thermal conductivity was determined for the same sample in the same direction.
Figure 15 shows the results of measurements of the thermoelectric properties at room temperature by the Harman method for samples sintered at 450˚C and pressure of 50 MPa. Bi content in BixSb2–xTe3 varied in the range of x from 0.3 to 0.5.
It is possible to see a monotonic increase in electrical conductivity as the concentration of Bi decreases. This is due to the fact that the major acceptors determining the electrical conductivity in p-type material are antisite defects of the metal in Te positions. The energy of formation of the structural defect 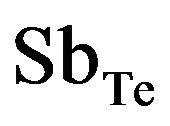 is less than that of
is less than that of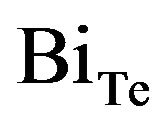 . Therefore the concentration of acceptor antisite defects increases with the increase of Sb content in solid solution, resulting in the increase of electrical conductivity. The Seebeck coefficient and thermal conductivity
. Therefore the concentration of acceptor antisite defects increases with the increase of Sb content in solid solution, resulting in the increase of electrical conductivity. The Seebeck coefficient and thermal conductivity
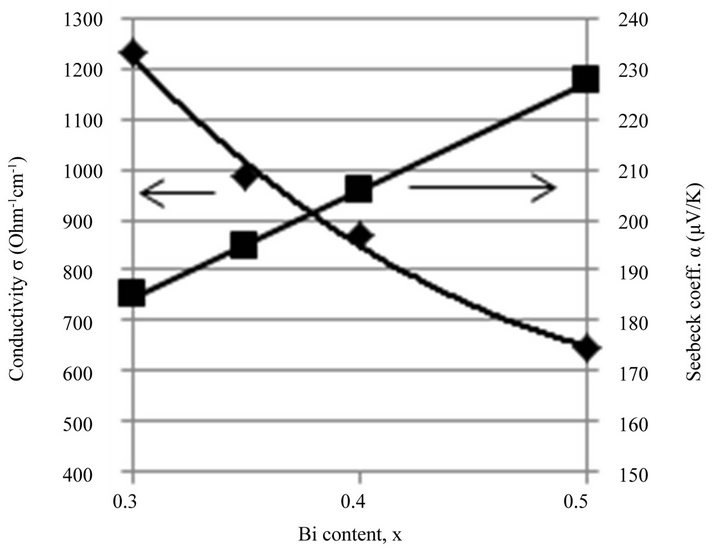
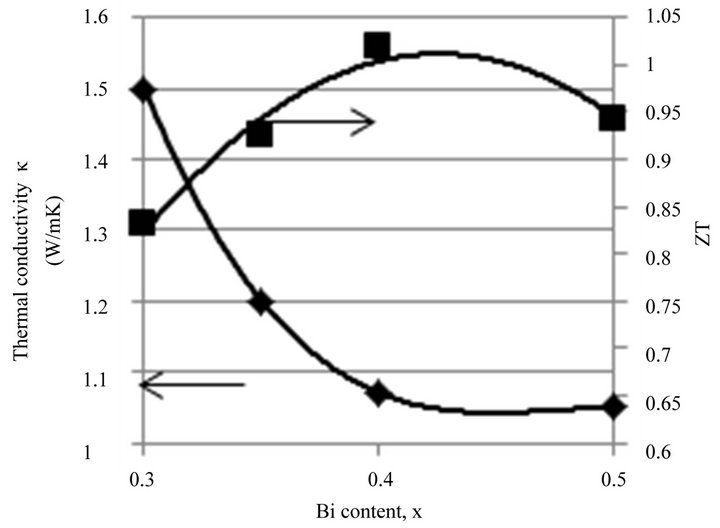
Figure 15. The dependence of thermoelectrical properties at room temperature of SPS samples sintered at temperature of 450˚C and pressure of 50 MPa on the composition of the solid solution BixSb2–xTe3.
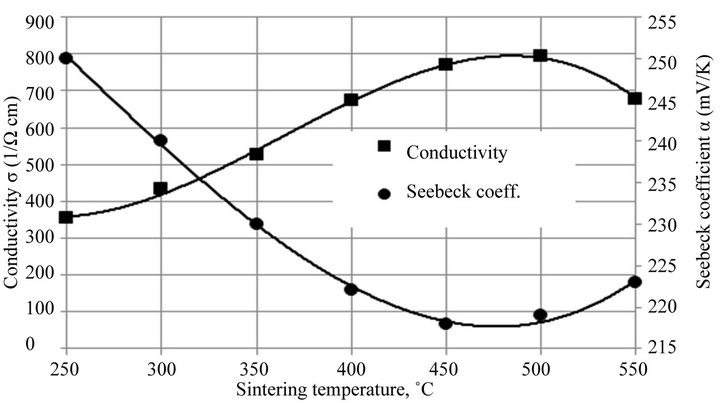
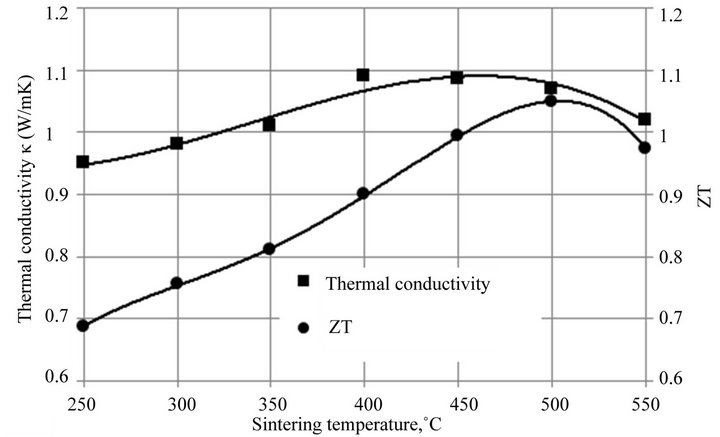
Figure 16. The dependence of electrical properties at room temperature of the samples Bi0.4Sb1.6Te3 on sintering temperature.
of the solid solution change accordingly. It is known that for single crystalline materials in the system BixSb2–xTe3 maximum figure of merit can be observed in the composition with x = 0.5. Moreover, to reduce the concentration of holes an excess of tellurium which is a donor is added. The value of the Seebeck coefficient for the optimum single crystal composition is in the range of 200 - 210 mV/K. For nanostructured samples of the same composition the Seebeck coefficient is much larger 230 - 240 mV/K. Taking into consideration the very slight change of the scattering parameter r, discussed above, this change can be attributed to donor effect of IPD. Therefore, the best properties for nanostructured samples are to be achieved with a larger content of Sb in comparison with a single crystal, and as Figure 15 shows, the nanostructured samples with composition Bi0.4Sb1.6Te3 possess the maximum thermoelectric efficiency.
For the samples of this composition, the dependence of the thermoelectric properties on the sintering temperature in the range of 250˚C to 550˚C is investigated. The results are shown in Figure 16.
7. Discussion
A completely new result is in the discovery of CSR grinding to the size smaller than 50 nm achieved by secondary recrystallization at the sintering temperatures above 400˚C. This process induced by interaction of structural defects is a self-organizing method to obtain nanostructured Bi0.4Sb1.6Te3. The advantage of this method of forming nanostructures is also in the fact that it takes place against the background of already formed at high temperature contacts between individual grains, when the area of the contact spot coincides with the area of the grain boundaries. Besides, the high-temperature sintering decreases the concentration of internal IPD produced by grinding the material. All this leads to the fact that to get good nanostructures and good electrical properties, it is necessary to perform compression at temperatures higher than 400˚C.
As the observed effect is stipulated by the defects formed during the preparation of the sample, it should be also observed in the preparation of nanostructured samples by hot pressing. One should keep in mind the difference in the time characteristics of the instrument in which the compaction of the samples is executed at SPS and hot pressing.
The question of any scattering at the boundaries of CSR and nanograins remains open. The achieved level of ZT for nanostructured polycrystals is close to the best results for single crystals, which seems a bit unusual if it is not attributed to this positive influence on the thermoelectric properties of the processes at the grain boundary. This impact should not be large, considering the small mean free path of the charge carriers in a single crystal, which at room temperature is about 5 nm for the direction perpendicular to the threefold axis and 2 nm for the parallel to threefold axis. The estimations of the mean free path of the phonons [37] also give approximately the same value (5 nm). At the maximum volume fraction of CSR, which is located at 50 nm, the difference between the dimensions of CSR and the mean free path seems to be not so discouraging. If there are processes, related to energy filtering of charge carriers [16] rather than to scattering, then the obtained at SPS size of CSR is very promising for the manifestation of the effects associated with these processes, since the mean free path for energy elastic scattering can significantly exceed the mean free path for a momentum. As the rapid increase in the mean free path manifests itself with decreasing temperature, all the effects connected with the influence of the boundaries of CSR and nanograins should be better expressed at low temperatures.
Nanostructured material can be represented as a twocomponent mixture of crystal grains either with conventional thermoelectric properties (micrograins) or with improved properties (nanograins). Individual nanograins can be isolated from each other, or they can be combined in a continuous chain if their concentration exceeds the percolation threshold. For all the models that describe the electrical or thermal conductivity of such systems [28,38], the resulting value is defined by mass concentration or, what is the same in our case, by volume fraction of the components. The measured CSR value is a volume fraction of nanocomponents and thus it is more informative from this point of view. It should be noted that the relatively small difference in the electrical or thermal conductivity of the components of the mixture (2 - 3 times) leads to the fact that the dependence on the volume fraction of the above mentioned models is linear in the volume fraction. There being a low volume fraction of nanoscale structures with small CSR, the resulting effect cannot be significant, even at high thermoelectric properties of nanoscale structures.
8. Acknowledgements
The authors thank V. T. Bublik for help in structural investigations and Z. M. Dashevsky and V. A. Kasian for help in low temperature measurements.
REFERENCES
- B. Poudel, Q. Hao, Y. Ma, X. Y. Lan, A. Minnich, B. Yu, X. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, “High-Thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys,” Science, Vol. 320, No. 5876, 2008, pp. 634-638. doi:10.1126/science.1156446
- S.J. Fan, J. Zhao, J. Guo, Q. Yan, J. Ma and H. Hоng, “Р-Type Bi0,4Sb1,6Te3 Nanocomposites with Enhanced Figure of Merit,” Applied Physics Letters, Vol. 96, No. 182104, 2008, pp. 456-459.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, “Bulk Nanostructured Thermoelectric Materials: Current Research and Future Prospects,” Energy & Environmental Science, Vol. 2, No. 5, 2009, pp. 466-479. doi:10.1039/b822664b
- Y. Lan, A. J. Minnich, G. Chen and Z. Ren, “Enhancement of Thermoelectric Figure-of-Merit by a Bulk Nanostructuring Approach,” Advanced Functional Materials, Vol. 20, No. 3, 2010, pp. 357-376. doi:10.1002/adfm.200901512
- W. Liu, X. Yan, G. Chen and Z. Ren, “Recent Advances in Thermoelectric Nanocomposities,” Nano Energy, Vol. 1, No. 1, 2012, pp. 42-56. doi:10.1016/j.nanoen.2011.10.001
- M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, “Perspectives on Thermoelectrics: From Fundamentals to Device Applications,” Energy & Environmental Science, Vol. 5, No. 1, 2012, pp. 5147-5162.
- Y. Horio, H. Yamashita and T. Hayashi, “Microstructure and Crystal Orientation of Rapidly Solidified (Bi,Sb)2 (Te,Se)3 Alloys by the Liquid Quenching Technique,” Materials Transaction, Vol. 45, No. 8, 2004, pp. 2757- 2760. doi:10.2320/matertrans.45.2757
- W. Xie, J. He, H. J. Kang, X. Tang, S. Zhu, M. Laver, S. Wang, J. R. D. Copley, C. M. Brown, Q. Zhang and T. M. Tritt, ”Identifying the Specific Nanostructures Responsible for the High Thermoelectric Performance of (Bi,Sb)2 Te3,” Nano Letters, Vol. 10, No. 9, 2010, pp. 3283-3289. doi:10.1021/nl100804a
- L. P. Bulat, V. B. Osvensky, G. I. Pivovarov, A. A. Snarskii and E. V. Tatyanin, “On the Effective Kinetic Coefficients of Thermoelectric Nanocomposites,” Proceedings of 6th European Conference on Thermoelectrics, Paris, 2-4 July 2008, pp. 12-1-12-6.
- L. P. Bulat, I. A. Drabkin, V. B. Osvensky, G. I. Pivovarov, A. A. Snarskii and E. V. Tatianin, “About Thermoelectric Properties of Bulk Nanostructures,” Thermoelectrics and Their Application, Sankt-Petersburg, 2008, pp. 39-43. (In Russian)
- L. P. Bulat, I. A. Drabkin, V. B. Osvensky and G. I. Pivovarov, “On Thermoelectric Properties of Materials with Nanocrystalline Structure,” Journal of Thermoelectricity, No. 4, 2008, pp. 26-34.
- L. P. Bulat, V. T. Bublik, I. A. Drabkin, V. V. Karatayev, V. B. Osvensky, G. I. Pivovarov, D. A. Pshenai-Severin, Е. V. Tatyanin and N. Yu. Тabachkova, “Bulk Nanostructured Thermoelectrics Based on Bismuth Telluride,” Journal of Thermoelectricity, No. 3, 2009, pp. 67-72.
- L. P. Bulat, G. I. Pivovarov and A. A. Snarskii, “Thermoelectrics Based on Fullerenes,” Thermoelectrics and Their Application, Sankt-Petersburg, 2006, pp. 39-40.
- L. P. Bulat, V. T. Bublik, I. A. Drabkin, V. V. Karataev, V. B. Osvenskii, Yu. N. Parkhomenko, G. I. Pivovarov, D. A. Pshenai-Severin and N. Yu. Tabachkova, “Bulk Nanostructured Polycrystalline p-Bi-Sb-Te Thermoelectrics Obtained by Mechanical Activation Method with Hot Pressing,” Journal of Electronic Materials, Vol. 39, No. 9, 2010, pp. 1650-1653. doi:10.1007/s11664-010-1250-0
- L. P. Bulat, I. A. Drabkin, V. V. Karataev, V. B. Osvenskii, Y. N. Parkhomenko, D. A. Pshenai-Severin, G. I. Pivovarov and N. Y. Tabachkova, “Energy Filtration of Charge Carriers in a Nanostructured Material Based on Bismuth Telluride,” Physics of the Solid State, Vol. 53, No. 1, 2011, pp. 29-34. doi:10.1134/S1063783411010082
- L. P. Bulat, D. A. Pshenai-Severin, V. V. Karatayev, V. B. Osvenskii, Yu. N. Parkhomenko, V. Lavrentev, A. Sorokin, V. D. Blank, G. I. Pivovarov, V. T. Bublik and N. Yu. Tabachkova, “Chapt. 23: Bulk Nanocrystalline Thermoelectrics Based on Bi-Sb-Te Solid Solution,” In: A. A. Hashim, Ed., The Delivery of Nanoparticles, INTECH, Rijeka, 2012, pp. 453-486.
- B. Yu, D. Z. Wang, G. Chen and Z. F. Ren, Y. Ma, Q. Hao, B. Poudel, G. Chen, Y. Lan, B. Yu, D. Wang and Z. Ren, “Enhanced Thermoelectric Figure-of-Merit in p-Type Nanostructured Bismuth Antimony Tellurium Alloys Made from Elemental Chunks,” Nano Letters, Vol. 8, No. 8, 2008, pp. 2580-2584. doi:10.1021/nl8009928
- V. T. Bublik, D. I. Bogomolov, Z. M. Dashevsky, I. A. Drabkin, V. V. Karataev, M. G. Lavrentiev, G. I. Pivovarov, V. B. Osvenski, A. I. Sorokin and N. Y. Tabachkova, “A Comparison of the Structure of the Thermoelectric Material Bi0.5Sb1.6Te3, Obtained by Hot Pressing and Spark Plasma Sintering,” Izvestia VUZov. Materialy Electronnoi Techniki, No. 2, 2011, pp. 61-65. (In Russian)
- V. T. Bublik, L. P. Bulat, V. V. Karataev, I. I. Maronchuk, V. B. Osvenski, Q. I. Pivovarov, D. A. Pshenai-Severin and N. Yu. Tabachkova, “On the Possibility of Saving the Nanostructured State in Obtaining Bulk Thermoelectric Materials Based on Bismuth and Antimony Chalcogenides,” Izvestia VUZov. Phisika, Vol. 53, No. 3/2, 2010, 37-41. (In Russian)
- Y. Lan, B. Poudel, Y. Ma, M. S. Dresselhaus, G. Chen and Z. Ren, “Structure Study of Bulk Nanograined Thermoelectric Bismuth Antimony Telluride,” Nano Letters, Vol. 9, No. 4, 2009, pp. 1419-1422. doi:10.1021/nl803235n
- B. M. Goltsman, B. A. Kudinov and I. A. Smirnov, “Semiconductor Thermoelectric Materials Based on Bi2Te3,” Nauka, Moskow, 1972, p. 320. (In Russian)
- A. N. Dubrovina and A. O. Teut, “Impurities in Thermoelectric Materials Based on Bi2Te3,” Izvestia AN SSSR. Neorganicheskie Materialy, Vol. 26, No. 6, 1990, pp. 1199-1203. (In Russian)
- L. D. Zhao, B. P. Zhang, J. F. Li, H. L. Zhang and W. S. Liu, “Enhanced Thermoelectric and Mechanical Properties in Textured n-Type Bi2Te3 Prepared by Spark Plasma Sintering,” Solid State Sciences, Vol. 10, No. 5, 2008, pp. 651-658. doi:10.1016/j.solidstatesciences.2007.10.022
- M. Stordeur, M. Srölzer, H. Sobottam and V. Rieder, “Investigation of the Valence Band Structure of Thermoelectric (Bi1-xSbx)2Te3 Single Crystals,” Physica Status Solidi (b), Vol. 150, No. 1, 1988, pp. 150-176. doi:10.1002/pssb.2221500120
- J. R. Drabble and R. Wolf, “Anisotropic Galvanomagnetic Effects in Semiconductors,” Proceedings of the Physical Society: Section B, Vol. 69, No. 11, 1956, pp. 1101- 1108.
- L. N. Luk’yanova, V. A. Kutasov, P. P. Konstantinov and V. V. Popov, “Thermoelectric Figure-of-Merit in p-Type Bismuth-and-Antimony-Chalcogenide Based Solid Solution,” Physics of the Solid State, Vol. 52, No. 8, 2010, pp. 1599-1605. doi:10.1134/S1063783410080068
- V. T. Bublik, Z. M. Dashevsky, I. A. Drabkin, V. V. Karataev, V. A. Kas’yan, M. G. Lavrent’yev, V. B. Osvenski, G. I. Pivovarov, D. A. Pshenai-Severin, A. I. Sorokin, N. Yu. Tabachkova and N. Bohmstein, “Transport Properties in the Temperature Range 10 - 300 K Nanostructured p-Bi0.5Sb1.5Te3, Produced by Spark Plasma Sintering,” Thermoelectrics and Their Application, SanktPetersburg, 2008, pp. 39-43. (In Russian)
- V. I. Odelevsky, “Calculation of Generalized Conductivity of Heterogeneous Mixtures,” Journal Technicheskoi Phisiki, Vol. 21, 1951, pp. 1379-1381. (In Russian)
- D. Stroud, “Generalized Effective Medium Theory for the Conductivity of an Inhomogeneous Medium,” Physical Review B, Vol. 112, No. 8, 1975, pp. 3368-3373. doi:10.1103/PhysRevB.12.3368
- T.-K. Xia, D. Stroud, “Theory of the Hall Coefficient of Polycrystals: Application to a Simple Model for La2-x MxCuO4 (M=Sr,Ba),” Physical Review B, Vol. 37, No. 1, 1988, pp. 119-122.
- V. T. Bublik, Z. M. Dashevsky, I. A. Drabkin, V. V. Karataev, V. A. Kas’yan, M. G. Lavrent’yev, V. B. Osvenski, G. I. Pivovarov, D. A. Pshenai-Severin, A. I. Sorokin, N. Yu. Tabachkova and N. Bohmstein, “Thermoelectric properties of nanostructured p-Bi0,5Sb1,5Te3, Obtained by Spark Plasma Sintering,” Thermoelectrics and Their Application, Sankt-Petersburg, 2008, pp. 53-57. (In Russian)
- A. V. Petrov, “Method for Measuring Thermal Conductivity of Semiconductors at High Temperatures,” Sbornik trudov I i II Soveshaniy po Thermoelectrichestvu, M-L, 1963, 27-32. (In Russian)
- T. C. Harman, “Spesial techniques for measurement of thermoelectric properties,” Journal of Applied Physics, Vol. 29, No. 8, 1958, pp. 1373-1374. doi:10.1063/1.1723445
- A. Abrutin, I. Drabkin and V. Osvenski, “Corrections Used when Measuring Thermoelectric Properties by Harman Method,” Proceedings of the 2nd Conference on Thermoelectric, Krakov, 15-17 September 2004, 5p.
- V. N. Abrutin, I. A. Drabkin, I. I. Maronchuk and V. B. Osvenski, “Measurement of Thermoelectric Samples by Harman Method,” Thermoelectrics and Their Application, Sankt-Petersburg, 2004, pp. 303-308. (In Russian)
- J. J. Shen, L. P. Hu, T. J. Zhu and X. B. Zhao, ”The Texture Related Anisotropy of Thermoelectric Properties in Bismuth Telluride Based Polycrystalline Alloys,” Applied Physics Letters, Vol. 99, No. 124102, 2011, pp. 356-359.
- L. P. Bulat, I. A. Drabkin, V. V. Karataev, V. B. Osvenskiǐ and D. A. Pshenaǐ-Severin, “Effect of Boundary Scattering on the Thermal Conductivity of a Nanostructured Semiconductor Material Based on the BiXSb2-XTe3 Solid Solution,” Physics of the Solid State, Vol. 52, No. 9, 2010, pp. 1836-1841. doi:10.1134/S1063783410090088
- G. N. Dulnev and Yu. P. Zarichnyak, “Thermal Conductivity of Mixtures and Composites,” Energiya, 1974. (In Russian)
NOTES
*Corresponding author.

