Received 22 July 2015; accepted 9 October 2015; published 15 October 2015

ABSTRACT

This paper provides a theoretical framework for explaining counterintuitive behaviors of a university choosing an unfavorable consequence in the long term while attempting to optimally allocate its resources in the short term. Our analysis demonstrates the process through which conflicting interests among different departments within an institution may lead to an internal allocation arrangement, which would not necessarily yield the highest possible outcome for the whole.

Keywords:

University Decision Making, Resource Allocation, Prestige Maximization

1. Introduction

Regardless of profit or non-profit nature of productive activities, every organization faces the challenge of achieving objectives through internally allocating limited resources. An institution of higher education, for instance, is recognized as a prestige-seeking entity allocating limited resources among academic units, while providing multiple products and services for their stakeholders, which include students, parents, communities, and governments [1] -[9] . Conflicting interests within a higher education institution, however, are documented in James [5] and Massy [6] , for different departments competing in a zero-sum game with the faculty trying to increase the prestige of only their particular department rather than the overall prestige of the institution. Moreover, Johnson and Turner [10] attribute differences in the number of tenure-track or tenured faculty across academic departments to political forces within the institution, which causes the “stickiness of the adjustment process”.

This paper lays out a simple theoretical framework for understanding a counterintuitive outcome of such conflicting behaviors leading to an unfavorable consequence while an institution attempts to optimally allocate resources into multiple activities. The analysis is carried out particularly with not-for-profit organizations such as higher education institutions and hospitals in mind, whose aims are considered to be serving the public need under financial constraints, yet seeking to improve social reputation or prestige [11] -[13] .

2. Prestige Function and Existence of the Optimal Allocation

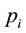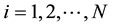Assume that an institution of higher education provides N distinguishable fields of study as well as functionally differentiated outputs such as student teaching, research, community services, or a mixture of these services, from which it gains separately independent prestige for. There exists no definite ceiling for achievable prestige, but it is assumed to be non-negative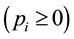, and let 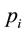be a continuous and strictly increasing function of financial input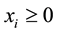, which is internally allocated to the ith field of activity. The value of prestige being equal to zero in a specific field i is equivalent to nonexistence of the activity within the institution,

and thus 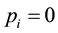only when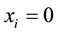. Let 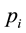be also regulated by, , 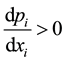and,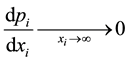

for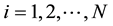. In other words, the prestige function 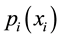is depicted as a typical S-shaped curve. The overall prestige of an institution is conceived as the sum of the partial prestige collected from each activity

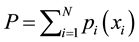, and the institution allocates the available resources, 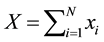, so as to maximize its overall prestige.

The basic setup formulated as above enables us to explore the optimizing allocation arrangement, which maximizes the overall prestige of an institution.¹ Considering that the institutional activities are bound by the

resource constraint, the optimization problem is simply denoted as

with the required first-order condition

(1)

The second-order condition for maximization

(2)

must also be satisfied for an arbitrary vector of, where δ indicates an infinitesimal change and satisfies. Then, we may state the following proposition.

Proposition 1. For a sufficiently small amount of available resources, a university never finds the optimal allocation set, which yields the highest possible institutional prestige.

Proof: See Appendix.

For intuitive validity of Proposition 1, assume a university with N = 2 and an allocation arrangement; that is, department 1 receives all the resources while department 2 receives none. Even if a small amount of the resources are transferred from department 1 and reallocated to department 2, i.e., , the level of prestige gained by department 2, , could be smaller than the prestige lost by department 1, , due to the S-shaped partial prestige curves. In such a scenario, the university concentrates all the resources into one department without being able to find the highest potential institutional prestige. The proof of Proposition 1 demonstrates that there exists such a threshold, i.e., , below which the solution to the optimization problem only finds the prestige “minimizing” allocation set.²

3. Optimal Allocation Set and Attainable University Prestige

In this section, we assume that the total financial resources granted to a university (by the state or other stakeholders) in one period is proportionate with the institutional prestige established in the previous period. The university strives for the highest possible overall prestige, as exemplified in global university rankings, through optimally allocating the available resources as much as the internal “adjustability” permits, which of course is confined by the internal rigidity existing due to conflicting interests among competing departments [5] [6] [10] . We examine whether the financial resources allocated repeatedly over time under such environments converge to any certain steady point.

3.1. Stable Management Point

Assume that the total budget granted to a university in period is determined according to the assessment of reputation or prestige demonstrated in the previous period. The total funding received by the university in

period is then represented by, where indicates the overall institutional prestige measured in period. Additional assumptions are imposed on the total resources that, , , and it is bounded above, thus approaching the least upper bound as which simply indicates that the amount of resources awarded to a university has a limit.

Suppose now that a university begins its operations at with the original allocation arrangement and.³ Given the initial resources and allocation, the university earns the total prestige in period, and the budget granted for the next period is determined as. We assume that the preliminary arrangement in period is made at the beginning of that period, based on the allocation rule applied to each department i,. The final arrangement in period is then made upon modifying the preliminary set in search of even higher attainable prestige than would otherwise be achieved with.⁴ The adjustment made from the preliminary allocations to the final arrangement is denoted by for all.

In practice, however, there might be internal rigidity in altering the allocation ratio assigned to each department, which makes it difficult for an institution to change the allocation composites drastically from the previously assigned ratios, as noted by Johnson and Turner [10] as “stickiness of the adjustment process”. Therefore, the modifications in the allocation arrangement may be realized only within a limited range of magnitude.

In order to accommodate such internal rigidity, the adjustment made from the initial allocation set to the final arrangement may be restrained by the following inequalities:

(3)

(4)

where is the overall prestige achievable with the preliminary allocations, and is the final overall prestige realized in period. The summations in the conditions (3)

and (4) are defined for all the departments for which the resource allocated in the previous period was not equal to 0. The inequality in (3) means that a large modification in the allocations does not occur unless a large increase in the total prestige can be expected as a result of the modified arrangement. The inequality in (4) simply describes the condition whereby even if a large increment would be obtained in the total prestige, the modification of the arrangement is limited by a certain ceiling. Both and are unique to each university and regu-

late the organizational adjustability to internally shift the allocations from the initial to the final set in a single period. Under these conditions, we are now ready to state the following proposition regarding the convergence of the process.

Proposition 2. Given any initial conditions, a university reaches the optimal allocation arrangement at which the maximal prestige is achieved: 1) with all departments, or 2) with only departments, where represents the number of department closures, or otherwise 3) no resources are allocated to any of the departments (i.e., the university ceases operations).

Proof: See Appendix.

What is stated in Proposition 2 appears a sterile result at first, but an important implication drawn from Proposition 2 is that the point of convergence may represent an inferior state for a university in terms of achieving the highest potential objective. In the following subsection, it is demonstrated for a heuristic example with, that a university may end up with optimizing at a “corner solution” where the institutional prestige realized as a result of “optimal” choices over time is lower than that yielded at the other corner solution.

3.2. An Example of Non-traditional Corner Solution

Suppose that a sufficiently funded university with departments is originally optimizing in the interior at. If the university resources plunge into a threshold, such as, in period due to a

severe budget cut, then the optimizing position shifts from the local maximum (point A) to the global minimum (point B) as depicted in Figure 1. The internal rigidity in settling financial matters, due to conflicting interests among competing departments, limits its mobility to shift the allocations within a certain capacity. Thus, the university moves toward a new allocation set, which yields the highest prestige, but it does so only within a limited range (indicated with “tick marks” in Figure 1 below).

Then, whether the new allocation set moves to the right or left from the prestige minimizing point B depends on the highest overall prestige found “within the mobility range”. In the graph, the new allocation set is reached

at point C, where the level of gained institutional prestige is the highest within the “ticked range”. If the institutional budget in period is determined by the overall prestige realized in the previous period, then the resources granted in period would be even smaller than the resources received in period. Beginning from point D in period, the highest institutional prestige within the mobility range is found at point E, where all the resources are concentrated into department 2, while department 1 is left with no funding, i.e., an allocation set.

As described so far, the process would typically repeat over the courses of modified allocations and corresponding overall prestige, ultimately reach the leftmost “corner solution” where the total budget is poured into only one of the two departments. As verified in this example, a university may well end up with an undesirable outcome in the long run even though the short-run optimizing process is achieved repeatedly. The result is dependent on the location of the initial allocation, internal adjustability which regulates the mobility range, as well as the shape of the total prestige curve in the neighborhood of new allocations.

4. Conclusion

This paper examines an important scenario, which a standalone institution of higher education is predicted to follow in order to achieve its potential maximal performance when the available resources are severely limited. Our result clearly indicates that a collection of multiple departmental performances does not necessarily yield the highest level of institutional prestige; that is, diversification of functional specialties is not necessarily the prudent approach to attaining the highest potential recognition when a university faces a scarcity in its financial resources. We also find that the limited internal adjustability caused by conflicting interests within a university impedes the goal of attaining the best outcome in the long term although the university “optimally” allocates its resources in the short term.

Acknowledgements

This paper was completed while S.P.W. was a visiting scholar at the University of California, Berkeley. We are grateful to colleagues at UC Berkeley for valuable comments and discussions on earlier drafts of the paper and would like to express sincere gratitude for all the encouragement and general resources provided by the Center for Studies in Higher Education and UC Berkeley.

Cite this paper

YasumiAbe,Satoshi P.Watanabe, (2015) Implications of University Resource Allocation under Limited Internal Adjustability. Theoretical Economics Letters,05,637-646. doi: 10.4236/tel.2015.55074

References

Appendix

Proof of Proposition 1

For all the fields of activities, place the corresponding values of partial prestige in decreasing order of for, where indicates the level of input maximizing the value of. That is, so that the last element in the order, , gives the lowest value of all.

Suppose the resource allocated to the Nth field is. Since, by the proposed construct, for, there exists an allocation for every such that, which lies to the left of. Denote such an allocation as as shown in Figure S1 below.

More explicitly,

(A1)

and the individually allocated resources sum to.

It is obvious that is continuous and strictly increasing over the domain, and. For the allocation arrangement with the budgetary constraint, the first-order condition (1) is satisfied by construct for all and, and the positive definite condition (2) for minimization is also satisfied. Thus, for a sufficiently small amount of available resources, i.e., where, there exists an allocation arrangement which minimizes the prestige of an institution.

For the uniqueness of the (global) minimum in the interior, suppose the total resources available for the institution is reduced further to an extremity such that. Under such an extreme condition, however the resource is allocated, every coordinate must lie on the left side of. For if this is not the case and even a single allocation lies on the right side of, it implies which by itself exceeds the total available resources. In order to simplify the notation in the following discussion, we denote.

Suppose there exists, other than, a different allocation set which yields the extremum under the same resource constraint. Since these allocations must satisfy, there exist for at least one such that and at least one j such that. If this is not the case, then it implies that the two allocation sets are identical, which contradicts the initial statement for the two sets being differentiated from each other. Since both and lie on the left side of while and also lying on the left side of, the following relation must be established for individual allocations, , , and,

(A2)

The result in (A2) clearly indicates, contradicting the required first-order condition (1), and so there exists no allocation set other than which yields the extremum under the budgetary constraint. This proves that for sufficiently small, the allocation set is the only arrangement capable of reaching the extremum, which turns out to be the global minimum found in the interior.

Suppose further that optimization is sought with the closures of departments. Then, the financial resources initially allotted to these departments would be redistributed among the existing departments with the same budgetary constraint. As a result of the closures of the fields, however, the relation is established, from which we find that the binding condition continues to be sustained for an operation of the activities. Therefore, the preceding result is preserved for the resource level, yielding the minimum as the only extremum in the interior.

Proof of Proposition 2

Let be the allocation arrangement made at the outset with the constraint. The partial prestige is defined by for, which sums to the overall institutional prestige. Then, the total resources received by the institution in period may be denoted as, based on which the new allocation arrangement is made. The initial and subjective allocation criterion at the beginning of a new period is transmitted from the immediately previous period for all, and modifications are made to the initial set in search of even higher prestige within the limited range of the organizational adjustability, reaching the final allocation set. This process may be applied iteratively for arbitrary large periods. Then, there exist only two possible scenarios to be considered.

Scenario 1.

Since for all, the preliminary total prestige evoked at the beginning of period is at least as large as the total prestige realized in the previous period; that is,. Because the modified allocation is made with additional adjustments to the preliminary set in search of even higher overall prestige, it is obvious that which in turn connects to the budget to be received in the next period,. A simple iteration of this process demonstrates that the total resources reveal a non-decreasing sequence, i.e., , for periods.

The equality for all periods in the above sequence is established only when, which means that the preliminary allocation set has in fact reached the (local) maximum and equals the previous allocation set. Since the initial allocation ratios are determined by the subjectively fixed criterion, the result gives. Thus, the equality holds only for the set giving the (local) maximum with, which is equivalent to the convergence of the sequence at the outset. Therefore, in the first scenario of a non-decreasing sequence, only the strictly increasing sequence of total resources, , remains to be examined.

Scenario 2.

If the total resources granted in period increase, , as a result of the allocation arrangement in period, then the sequence begins to strictly increase afterwards. This is equivalent to the first scenario with a strictly increasing sequence. If the equality holds, the preliminary allocation in period is given by for all because of the subjectively assigned criterion. Since the preliminary prestige in period is the same as the total prestige realized in period, i.e., , the relation must hold after the modifications are made from the preliminary set to the final arrangement. The equality between the prestige in two periods, , is established only if the modifications would produce no increment in the total prestige, which implies that the set has in fact yielded a (local) maximum and no further reallocation would be sought thereafter. In this case, the total resources become, for, which clearly indicates the convergence of the sequence. If the total prestige is strictly increasing, , then the total resources also increase strictly, , and the sequence begins to reveal a strictly increasing pattern as in the first scenario. Finally, if, then the relation between and must be examined through the same process described above.

To summarize both scenarios, other than the clearly convergent cases, the total resources evolve in one of the following paths:

・ Strictly increasing

・ Strictly decreasing up to a certain point, then strictly increasing thereafter

・ Strictly decreasing

The common feature for all three paths is that they eventually turn to monotone sequences (either strictly increasing or decreasing). Since the sequence is bounded below and has the least upper bound, the sequence is convergent either way.⁵ If is strictly increasing, then it approaches a constant limit, whereas if is strictly decreasing the sequence converges either to 0 or a non-zero limit. If converges to 0, it clearly means that every allocation in converges to 0. Therefore, it suffices to only examine the cases where is a monotone sequence and convergent to a non-zero limit.

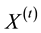
We first note that convergence of means the convergence of because the total resource is a continuous function of the total prestige,. We now examine how the resources and allocations progress over time. The overall change in the allocation arrangement from period to period is decomposed into

two separate movements from the set to and from to the final arrangement. Let and represent such modifications made at each stage,

(A3)

(A4)

with corresponding changes in the total prestige

(A5)

(A6)

Substituting the definition in equation (A3) yields

(A7)

Therefore, the convergence of sequence results in convergence of to 0 in the above relation (A7), which in turn implies that, thus its summation in (A5), also converge to 0. Furthermore, a combined definition of (A5) and (A6) yields. The finding that converges to 0, along with the convergent sequence, implies converges to 0. Since we are examining the cases where the sequence converges to a non-zero limit, the allocation is not equal to 0 for all. Then, the denominator of the right-hand side in (A8) below, which is simply a rewritten form of the rigidity condition (3) for period,

(A8)

has a positive sign, which affirms that the right-hand side of the inequality in (A8) converges to 0. This means that on the left-hand side also converges to 0, and so we have shown that both and converge to 0. Finally, using the relation which is drawn from the definitions (A3) and (A4), we have proved that converges.

If the point of convergence does not yield any of 1), 2), and 3) stated in Proposition 2, the value of prestige added by the modification process from to is arbitrarily large near, which contradicts the fact that both and converge to 0. Therefore, the allocation set approaches one of 1), 2), and 3) in Proposition 2, which we shall call the stable management point to signify its stability as the allocation set enabling an institution to operate at its maximal prestige, except for the case 3).

NOTES

¹Abe and Watanabe [14] , based on this framework, demonstrate that enhancement of interdisciplinary effort may hinder prestige maximization of a university, through misallocation of internal resources.

² indicates the level of input maximizing the value of . See Proof of Proposition 1 in Appendix for details.

³For notational simplification in this and following sections, we write to denote.

⁴Thus, we assume that the preliminary arrangement is made in each period at first, based on the subjective criterion. The shift in the allocations made from the initial set to the final arrangement may be considered as modifications for accommodating the discrepancy found between the subjective and objective assessment results.

⁵This is simply the result of the Monotone Convergence (Sequence) Theorem, which states that every bounded monotone sequence in R converges to an element of R.