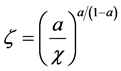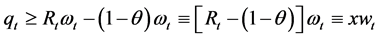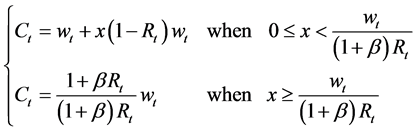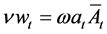Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:51629,9 pages
10.4236/tel.2014.49097
Credit Markets Development and Economic Growth: Theory and Evidence
Seifallah Sassi
Laboratory of Applied Economics and Finance, University of Carthage, Tunis, Tunisia
Email: seifallah.sassi@yahoo.fr
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2014; revised 7 September 2014; accepted 1 November 2014
ABSTRACT
The purpose of this paper is to study jointly the effects of consumer credit market and investment credit market on economic growth. We introduce consumer credit market in Schumpeterian frame- work. Under credit market imperfections, our model predicts a negative effect of the development of consumer credit market and a positive effect of the development of investment credit market on economic growth. We next confront the model on a panel of 27 European’s countries over the period 1995-2012. Using GMM dynamic panel data estimation, empirical results confirm our theo- retical predictions. Credit composition may give explanation of the ambiguous credit-growth nexus and its heterogeneity across country.
Keywords:
Credit Markets Development, Economic Growth, Consumer Credit, Investment Credit, Panel Data

1. Introduction
Major theoretical literature on financial development and economic growth supports the argument that credit market development has a positive effect on economic growth by enhancing capital accumulation and technological changes. A general consensus exists among economists that a well-developed credit system spurs economic growth by improving resources allocation channeled into investment, reducing information and transaction costs and allowing risk management to finance riskier but more productive investments and innovations. However, recent empirical studies don’t support the finance-led growth hypothesis. This finding is considered as a puzzle for theories underpinning for the importance of credit market development for growth. This conflicting finding is proved by a number of recent papers.
Using GMM dynamic panel data estimation and Pooled Mean Group estimator, with two indicators of financial development, Favara (2003) [1] found no evidence on the impact of financial development on growth pattern and concluded that the conventional positive causality of financial development on economic growth was based on average effects which vary varied according to the sample and the period considered and the techniques used.
Loayza and Rancière (2006) [2] have provided evidence, on a sample of 75 countries during the period 1960- 2000, that the impact of private domestic credit on economic growth is significantly positive in the long run but significantly negative in the short-term.
Ben Naceur and Ghazouani (2007) [3] and Saci et al. (2009) [4] , used dynamic panel models on respectively, 11 MENA countries and 30 developing countries, and find evidence of a positive effect of stock markets development but a meaningful negative effect of bank development on growth.
In presence market imperfections, credit market development isn’t able to lead the expected effect on growth. Credit market imperfections are mainly asymmetric information, adverse selection, high information, transaction, and monitoring costs and credit market repression in the form of borrowing constraints imposed by government interventions. Asymmetric information and high transaction costs led to interlinkage of markets which reduced the degree of competition in the economy (Braverman and Stiglitz, 1982 [5] ). Bernanke, Gertler and Gilchrist (1999) [6] showed the imperfections add persistence to the macroeconomic dynamics. Credit constraints have distributional impacts on the business cycles and thereby volatility and growth Aghion and Banerjee (2005) [7] . A particularly important consequence of such imperfections is the existence of credit rationing. With rationed credit markets, the business cycle is amplified and the long-term investment becomes procyclical. Thus, these imperfections seem to have serious implications on the growth path in developing and developed countries.
Empirical studies use generally credit to private sector as proxy of credit market development and don’t distinguish the specific effect of each credit market, consumer and investment credit markets, on economic growth. Certainly, investment and consumer credit have different effects on economic development and a specific transmission channel. Schumpeter (1911) [8] believed that the credit to enterprise was the necessary premise for the realization of the innovative processes. Jappelli and Pagano (1994) [9] argued that alleviating credit constraints on households reduced the savings rate, with negative repercussions for economic growth. Galor and Zeira (1993) [10] provided evidence that consumer credit could affect positively economic growth only if it’s invested in human capital and/or microenterprises. Using a dataset of 45 developed and developing countries, Beck, Büyük- karabacak, Rioja et Valev (2012) [11] found evidence that investment credit raised economic growth whereas household credit had no significant effect on real-economy performance. Dos Santos P. (2011) [12] was one of the pioneers who examined the distinctive transmission channel of investment and consumption credit using a Marxian framework. He showed that economies with higher relative share of consumption credit would generally suffer from a lower rate of net credit extension and higher levels of financial risk than comparable economies.
This paper aims to investigate this field in the attention to provide theoretical and empirical explanations to the credit-growth puzzle. To do so, we investigate the relationship between credit markets development and eco- nomic growth in the presence of financial markets imperfections. We introduced consumer credit market in the theoretical framework of Aghion, Howitt and Mayer Foulkes (2005) [13] ; and we considered credit market imperfections in both, consumer and investment credit markets. The result is a Schumpeterian model with two period overlapping generations, in which each credit market has a specific effect on economic development. The model predicts that the development level of consumer credit market has a negative effect on convergence to the technology frontier thus on economic growth whereas the development level of investment credit market has a positive on growth. These causalities are maintained till the development level of credit market reaches the optimum; after that, credit markets development will have no effect on economic development. These predictions were tested and supported empirically using system GMM estimators of dynamic panel on cross-sectional data of 27 European countries during the period 1995-2012.
The paper is organized as follows. In Section 2, we develop the theoretical framework of Aghion et al. (2005) [13] by introducing consumer credit market in the model. Section 3 tests empirically the theoretical implications of the model using panel data of European countries. Section 4 is the conclusion.
2. The Model
We develop the two-period overlapping generations model of Aghion et al. (2005) [13] . The framework supposes that between m economies in the world, there are only exchanges of technological ideas. The population of each country P is fixed and normalized to unity. Each generation is composed of two types of agents, lenders and borrowers. Borrowers are further divided into two groups as consumers and entrepreneurs who differ in their preferences. Each of the labor market, capital market, and the loans market is a competitive market.
2.1. The General Sector
There is one multi-purpose “general” good, produced according to the production function:
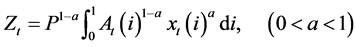 (1)
(1)
where
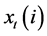 is the input of the latest version of intermediate good
is the input of the latest version of intermediate good
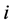 and
and
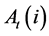 is the productivity parameter associated with it.
is the productivity parameter associated with it.
The general good is used for consumption and as input to product and develop the intermediate goods. Since the general good is produced under perfect competition, the price of an intermediate good will be:
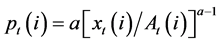 (2)
(2)
2.2. Intermediate Sectors
If in an intermediate sector, there is a successful innovation, the productivity of this sector will equal the productivity at the world technology frontier
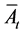 which grows with a positive constant rate. Therefore, the productivity of a sector
which grows with a positive constant rate. Therefore, the productivity of a sector
 evolve according:
evolve according:
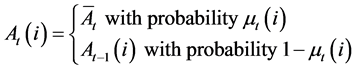
In each intermediate sector, there some people who are able to produce a new version of intermediate good for a unit cost equal to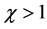 . We assume that the market price of the last generation intermediate good will be
. We assume that the market price of the last generation intermediate good will be . So the quantity demanded will be:
. So the quantity demanded will be:
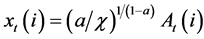 (3)
(3)
An unsuccessful innovator will earn nothing and the profit of a successful innovator will be:
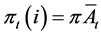 (4)
(4)
where
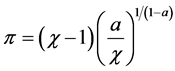
2.3. Aggregate Behavior
For notational convenience, “average productivity” is defined as:
 (5)
(5)
Let’s assume that at equilibrium the probability of innovation will be the same for all intermediate sector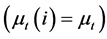 ; so average productivity will be equal to:
; so average productivity will be equal to:
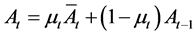 (6)
(6)
The technology gap is defined as: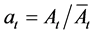
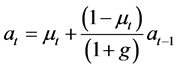
Therefore the production function (1) of the “general” good can expressed as:

where où
Under perfect competition, the wage rate will be:
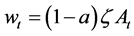
2.4. Innovation
Let’s define R&D investment function as:
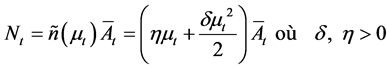
where

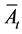
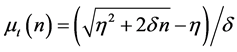
And his expected net payoff is given as:
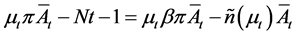
2.5. Credit Markets
For analytical convenience, it is assumed that banks operate at no cost and they don’t earn profit. Thus interest rates for lenders and borrows are the same and equal to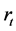
2.5.1. Consumer Credit Market
1) Consumer Credit Market Imperfections
To introduce credit market imperfections, we suppose that there are some dishonest agents who are able to sacrifice a proportion
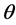
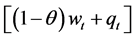
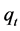
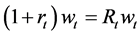
Obviously, if
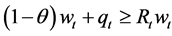
All consumers will apply for a loan then miss repayment if the credit is granted. So banks impose a natural credit constraint on consumers and set credit at fixed proportion

We represent the development of Consumer Credit market by the cost parameter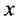
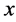
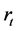
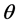
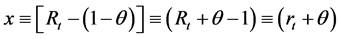
This means that, in one hand, banks are able to supply more credit and take more risk by increasing interest rate
2) Supply of Consumer Credit
Each consumer is endowed with one unit of labor in his first period of life. His wage rate
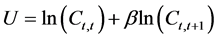
where
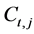
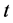
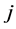
Since consumer has no endowment in his first period of life, his is obliged to apply for a credit. Thus, with no credit constraints, the optimal consumption is the solution of this system:

The optimal plan for consumers is to consume
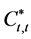
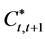


From Equation (14), the credit size supplied at the first period equal to
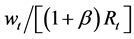
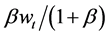
Therefore, under perfect credit market, the total optimal consumption for an agent:
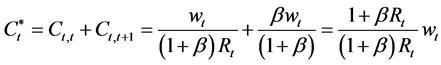
Now, under credit market imperfections, the credit granted,
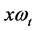
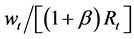
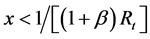
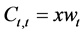
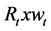
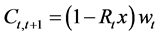
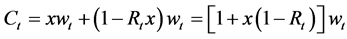
Since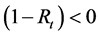
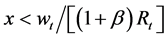
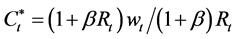
Therefore, the total consumption evolves according to:
The development level of consumer credit market
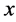
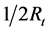
2.5.2. Investment Credit Market
1) Investment Credit Market Imperfections
Each entrepreneur is endowed with a wage rate at the end of his first period of life. To invest

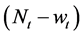
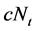
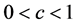
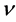
where v depends positively on the hiding cost
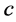
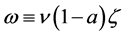
The development level of investment credit market is represented by parameter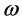
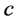
2) Supply of Investment Credit
In equilibrium and under perfect credit market, an entrepreneur will choose the probability
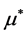

The optimal R&D investment equal to:
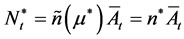
where
But with credit market imperfections, an entrepreneur is credit rationed if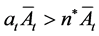
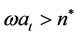

And he will innovate with probability:
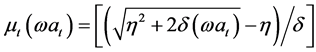
Therefore, the investment evolves according to:
The development level of investment credit market
2.6. Credit Markets Development and Economic Growth
For closed economy without government, we can write the GDP per capita as:
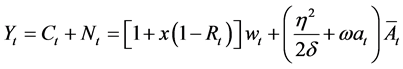
Therefore GDP per capita is a decreasing function of the development level of consumer


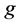
3. Empirical Evidence
3.1. Methodology
To test our theoretical model, we use a second-order Taylor expansion to approximate
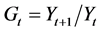
Our theoretical model is approximated by the following growth regression:
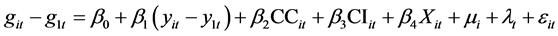
where g denotes the growth rate of per-capita GDP, y the initial log of per-capita GDP, CC the log of consumer credit, CI the log of investment credit and X a set of control variables. Control variables used in our econometric investigation are GC the log of government consumption to GDP, INF inflation rate and Trade the log of the ratio of exports plus imports to GDP. Country 1 is the technology leader.
Given the specification of Equation (23), our regression is considered as a dynamic panel model. So, efficient estimators are given through the generalized method of moments. Arellano and Bover (1995) [14] and Blundel and Bond (1998) [15] shows that the system GMM estimator provide a more efficient estimator than the difference GMM estimator. The estimates were made by the one step and two step system GMM. In the one-step estimator, the error term
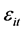
As a robustness check, we use data over five years instead of annual to prevent any biased estimates and to capture business cycle movements.
An important step that is relevant to the estimation of our model is to conduct M2 test, Sargan test, Hansen test and Kleibergen-Paap tests. The M2-test checks problem regarding the second-order serial autocorrelation of the error terms. The sargan test verifies that the instruments used are not correlated with the residuals. The Hansen test and the Kleibergen-Paap test provides statistics for weak instruments due to an over-identification and under-identification, respectively.
3.2. Data
Our model is tested a balanced sample of 27 European’s countries3 over the period 1995-2012. Germany is considered as the leader of the 27 European’s countries in our sample. Disaggregated data on credit were extracted from Europeen Credit Research Institute Database. The WDI-World Bank database is the source for other macroeconomic variables. Table A1 and Table A2 in Appendix report respectively summary statistics and empirical correlations between variables.
The dataset shows that growth rate of GDP per capita is negatively correlated with consumer credit and positively correlated with investment credit. Macroeconomic indicators have the expected correlation sign with the economic growth: growth rate of GDP per capita is negatively correlated with government consumption as inflation and positively correlated with trade.
3.3. Empirical Results
The results from estimating Equation (23) are reported in Table 1. System GMM regressions on annual data are reported in columns (1) and (2). These results confirms theoretical predictions and show that consumer credit has a significant negative effect on convergence to the leader growth rate and investment credit promotes positively the convergence at 5% significance level for the two specifications, one step and two step system GMM. In regression (3) and (4), we use data over five years instead of annual as a robustness check and to capture business cycle movements. Columns (3) and (4) confirm our main findings: consumer credit affects negatively and significantly the catch-up of technological frontier however investment credit has a positive effect.
Our findings give an explanation of the ambiguous credit-growth nexus in empirical literature since its uses aggregate credit to private sector as proxy of credit market development. Empirical studies must consider credit composition and study a distinctive effect of each market. In developed and developing countries, consumer credit market continues has an “explosive” trend while investment credit market show weak growth rate.
Theory provide evidence about the positive effect of investment credit on economic growth through capital accumulation, productivity growth and resource allocation but the effect of consumer credit on economic growth is ambiguous. Using a sample of 25 countries, Jappelli and Pagano (1994) [9] provide evidence that the development of consumer credit market has a negative effect on economic growth through reducing saving rate. Galor and Zeira (1993) [10] and De Gregorio (1996) [17] show that consumer credit affect positively economic growth only if it’s invested in human capital and/or microenterprises.
Furthermore, our findings provide also a clarification of theheterogeneity of credit-growth nexus across country. This can be explained by the disparity of the composition of credit across country and sample.
Our results shows that a negative relationship between relative growth rate and the initial GDP per capita relative to the leader. Thus the hypothesis of conditional convergence is validated. This concept assumes that each country converges to its own long-run equilibrium path and record a high growth rate when it’s far from the path.
Table 1. Dynamic panel-data estimation dependent variable: relative growth rate to the leader
T-Student are reported in parentheses. ***, **, and * indicate significance levels at 1, 5, and 10 percent, respectively. For the M2 test for autocorrelation, the null hypothesis is that the errors in the first-difference regression exhibit no second-order serial correlation. For Sargan test, the null hypothesis is that the instruments used are not correlated with the residuals. For the Kleibergen-Paap test of under-identification, the null hypothesis is that the instruments used are potentially weak. For Wald Test, M2 test, Sargan Test, Hansen Test and the Kleibergen-Paap test the p-values are reported.
The control variables have the expected sign and are tightly estimated. The harmful effect of inflation rate on economic growth is confirmed by a negative and significant sign in the two specifications of the GMM estimator. Government consumption has a positive and significant effect on economic growth at least at 5% level in all specification. This finding proves that public consumptions in European countries are spending mainly in investment and infrastructure which improve economic growth (Kneller, Bleaney, and Gemmell, 1999 [18] ). The trade openness is positively correlated to economic growth. Trade openness boosts economic growth by facilitating the exchange of goods and services and by improving capital allocation efficiency.
Our results are robust: M2 confirms the absence of a second-order serial correlation of the residuals in the differenced regression. The Sargan test confirms no correlation between the used instruments and the residuals. Finally the Hansen and the Kleibergen-Paap test do not detect any problem of over-identifications and under- identifications restrictions and confirm the validity of variables in differences and in levels as instruments in system GMM.
4. Conclusions
This paper attempts to distinguish the specific effect of consumer and investment credit markets on economic growth. We develop the theoretical framework of Aghion et al. (2005) [13] by introducing consumer credit market in the model and by considering credit market imperfections in both, consumer and investment credit markets.
The model predicts that the development level of investment credit market affects positively convergence to the technology frontier, however, consumer credit market development affects negatively convergence. On a balanced sample of 27 European’s countries over the period 1995-2012, estimations were conducted using system GMM on annual data and data over five years. Empirical results produce evidence to support our predictions: Credit market promotes economic growth by lending to productive enterprises whereas consumer credit has a significant negative effect on real-economy performance. Our findings provide a missing piece of the credit-growth puzzle. The positive effect of investment credit market is dampening by the reverse relationship between consumer credit market and economic growth.
Banks must control the credit composition and the growth rate of the relative share of consumer credit. The increase of consumer credit induced a decline in the trade balance (Büyükkarabacak & Krause, 2009 [19] ) and a high level of financial volatility (Büyükkarabacak & Valev, 2010 [20] ).
References
- Favara, G. (2003) An Empirical Reassessment of the Relationship between Finance and Growth. International Monetary Fund Working Paper Series, 1-46.
- Loayza, N.V. and Ranciere, R. (2006) Financial Development, Financial Fragility, and Growth. Journal of Money, Credit and Banking, 38, 1051-1076. http://dx.doi.org/10.1353/mcb.2006.0060
- Ben Naceur, S. and Ghazouani S. (2007) Stock Markets, Banks and Growth in Some Mena Region Countries. Research in International Business and Finance, 21, 297-315. http://dx.doi.org/10.1016/j.ribaf.2006.05.002
- Saci, K., Giorgioni, G. and Holden, K. (2009) Does Financial Development Affect Growth? Applied Economics, 41, 1701-1707. http://dx.doi.org/10.1080/00036840701335538
- Braverman, A. and Stiglitz, J. (1982) Sharecropping and the Interlinking of Agrarian Markets. American Economic Review, 72, 695-715.
- Bernanke, B.S., Gertler, M. and Gilchrist, S. (1999) The Financial Accelerator in a Quantitative Business Cycle Frame- work. In: Taylor, J.B. and Woodford, M., Eds., Handbook of Macroeconomics, 1341-1393.
- Aghion, P. and Banerjee, A. (2005) Volatility and Growth. Oxford University Press, Oxford. http://dx.doi.org/10.1093/acprof:oso/9780199248612.001.0001
- Schumpeter, J.A. (1911) The Theory of Economic Development. Cambridge.
- Jappelli, T. and Pagano, M. (1994) Saving, Growth, and Liquidity Constraints. Quarterly Journal of Economics, 106, 83-109. http://dx.doi.org/10.2307/2118429
- Galor, O. and Zeira, J. (1993) Income Distribution and Macroeconomics. Review of Economic Studies, 60, 35-52. http://dx.doi.org/10.2307/2297811
- Beck, T., Büyükkarabacak, B., Rioja, F. and Valev, N. (2012) Who Gets the Credit? And Does It Matter? Household vs. Firm Lending across Countries. The B.E. Journal of Macroeconomics, 12, 1-46.
- Dos Santos, P. (2011) Production and Consumption Credit in a Continuous-Time Model of the Circuit of Capital. Research on Money and Finance, Discussion Paper No. 28.
- Aghion, P., Howitt, P. and Mayer-Foulkes, D. (2005) The Effect of Financial Development on Convergence: Theory and Evidence. Quarterly Journal of Economics, 120, 173-222.
- Arellano, M. and Bover, O. (1995) Another Look at the Instrumental Variable Estimation of Error-Components Models. Journal of Econometrics, 68, 29-51. http://dx.doi.org/10.1016/0304-4076(94)01642-D
- Blundell, R. and Bond, S. (1998) Initial Conditions and Moment Restrictions in Dynamic Panel Data Models. Journal of Econometrics, 87, 115-143. http://dx.doi.org/10.1016/S0304-4076(98)00009-8
- Windmeijer, F. (2005) A Finite Sample Correction for the Variance of Linear Efficient Two-Step GMM Estimators. Journal of Econometrics, 126, 25-51. http://dx.doi.org/10.1016/j.jeconom.2004.02.005
- De Gregorio, J. (1996) Borrowing Constraints, Human Capital Accumulation and Growth. Journal of Monetary Economics, 37, 49-71. http://dx.doi.org/10.1016/0304-3932(95)01234-6
- Kneller, R., Bleaney, M. and Gemmell, N. (1999) Fiscal Policy and Growth: Evidence from OECD Countries. Journal of Public Economics, 74, 171-190. http://dx.doi.org/10.1016/S0047-2727(99)00022-5
- Büyükkarabacak, B. and Krause, S. (2009) Studying the Effects of Household and Firm Credit on the Trade Balance: The Composition of Funds Matters. Economic Inquiry, 47, 653-666. http://dx.doi.org/10.1111/j.1465-7295.2008.00173.x
- Büyükkarabacak, B. and Valev, N.T. (2010) The Role of Household and Business Credit in Banking Crises. Journal of Banking and Finance, 34, 1247-1256. http://dx.doi.org/10.1016/j.jbankfin.2009.11.022
Appendix
Table A1. Summary statistics.
Table A2. Pairwise correlation matrix.
NOTES
1It’s supposed that
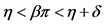
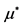
2
3Austria, Belgium, Bulgaria, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Latvia, Lithuania, Luxembourg, Malta, Netherlands, Poland, Portugal, Romania, Slovak Republic, Slovenia, Spain, Sweden, United Kingdom.