Theoretical Economics Letters
Vol.05 No.01(2015), Article ID:53710,3 pages
10.4236/tel.2015.51005
Financial Intermediaries in a Search Theoretic Model of Bilateral Exchange
Andrew C. Chang
Division of Research and Statistics, Federal Reserve Board, Washington DC, USA
Email: a.christopher.chang@gmail.com


ABSTRACT
Received 9 December 2014; accepted 28 January 2015; published 30 January 2015
This note investigates an effect of financial intermediaries on bilateral exchange. In a search theoretic framework, it is possible for Pareto inefficient outcomes in bilateral exchanges between firms and laborers, when firms are forced to secure liquidity through financial intermediaries and are unable to communicate the value of the firm to the intermediary. The quantity of labor supplied to firms in the model is below the Pareto optimal level.
Keyword
Search Theory

1. Introduction
Financial intermediaries are thought to facilitate market transactions through the provision of liquidity, which may lead to the optimal level of investment by firms. However, the actual level of liquidity provided by financial intermediaries may be sub-optimal when there exist information asymmetries between the firm and the intermediary [1] . This problem becomes more acute when the asymmetric information among firms becomes greater, as when firms finance projects for research and development [2] .
This note shows that it is possible for Pareto inefficient outcomes in bilateral exchanges between firms and laborers when firms must secure liquidity to hire laborers through financial intermediaries and the firms are unable to communicate their value with the financial intermediaries. In a search theoretic framework, the quantity of labor supplied to firms is below the Pareto optimal level.
In the model, there are firms, laborers and intermediaries. Firms exchange wages for labor from laborers. However, to finance wages, firms must borrow from intermediaries. As intermediaries do not know the true value of the firm and capital accumulation is costly, they form contracts with the firms with terms that lead to a Pareto inefficient amount of output. This note adds to the literature on financial intermediaries [3] [4] .
2. The Environment
Time is discrete and continues forever. There are three types of agents: firms, laborers, and intermediaries. Each agent is infinitely lived and there are continuums of each type of agent on a unit measure. Every period is characterized by two sub-periods. Following [5] , I label the first sub-period the day market (DM) and the second sub-period the centralized market (CM).
Every agent is rational and maximizes some objective function. Agents discount between periods at a time- invariant rate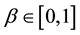 , and do not discount within a period (that is, do not discount between the DM and the CM).
, and do not discount within a period (that is, do not discount between the DM and the CM).
Firms are profit maximizing and produce a single output good y according to the production function
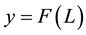 , where L is labor. Output is sold in a perfectly competitive market at price
, where L is labor. Output is sold in a perfectly competitive market at price . The production function for the firm satisfies the usual convexity assumptions and transversality conditions:
. The production function for the firm satisfies the usual convexity assumptions and transversality conditions: ,
,
 ,
,
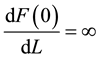 , and
, and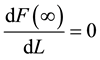 . The production function is also normalized such that
. The production function is also normalized such that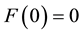 .
.
Laborers produce labor at cost −c(L) with similar assumptions on convexity and transversality: ,
,
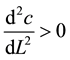 ,
,
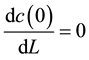 , and
, and . Laborers derive a positive utility from wages w, assumed to be linear and separable from c(L). As with firms, c(0) is normalized to 0.
. Laborers derive a positive utility from wages w, assumed to be linear and separable from c(L). As with firms, c(0) is normalized to 0.
Intermediaries loan money m to firms in the DM and are repaid by firms a sum r in the CM. Intermediaries cannot produce goods and must sign contracts with firms in order to consume. Intermediaries extract a fraction of the surplus from the trade between firms and laborers through a transfer of profits from the firm to the intermediary. Intermediaries are risk averse and raising capital costs the intermediary h(m), where the same assumptions on convexity and transversality apply to h(m) as c(L)1. There is a non-negativity constraint on all relevant variables: r, m, L, and w.
The timing of events is as follows: at the beginning of the DM firms and laborers form a bilateral match. Each firm may only be matched to at most one laborer in each period. In a symmetric fashion, each laborer may only be matched to at most one firm in a given period. Each firm is also matched with an intermediary.
After firms and intermediaries are matched, the intermediary proposes a contract to the firm {r, m} where m is the monetary loan from the intermediary to the firm to be loaned in the DM and r is the eventual repayment in the CM. There is perfect contract enforcement. Firms may either accept or reject this offered contract. Accepting the contract allows firms to purchase labor from laborers to produce according to the production function . Rejecting the contract results in zero production for the firm that period as firms are unable to hire labor without money from the intermediary.
. Rejecting the contract results in zero production for the firm that period as firms are unable to hire labor without money from the intermediary.
If a firm decides to accept the contract, then the firm may use the loan money m from the intermediary to offer a wage w to the laborer. The firm may only use the loaned money from the intermediary to offer a wage, so 0 ≤ w ≤ m. In return for consuming wage w in the DM, laborers supply labor L to the firm in the CM, which the firm can use to produce its output at the rate F(L). Firms and laborers use a generalized Nash bargaining solution to determine the distribution of surplus from this trade. The generalized Nash solution at period t follows Equation (1) for some
 2.
2.
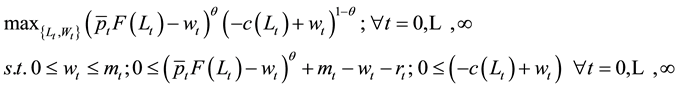 (1)
(1)
After firms produce and sell their output in the CM, firms repay the loan repayment amount r to the intermediaries. At the end of the period, all matches are destroyed and the cycle repeats again next period. Each variable r, m, L, and w can be offered in perfectly divisible units.
The objective functions for firms, labors, and intermediaries are shown in Equations (2), (3) and (4)3.
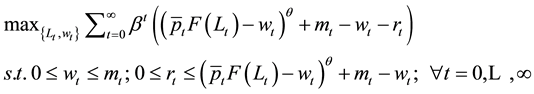 (2)
(2)
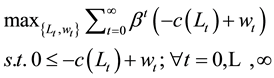 (3)
(3)
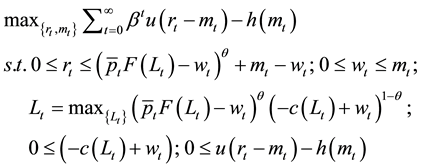 (4)
(4)
Consistent with asymmetric information between lenders and borrowers, I assume that intermediaries have imperfect knowledge about the firm and can only observe that the firm requires
 to optimize profits, where
to optimize profits, where
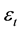 is white noise.
is white noise.
In this context, θ represents the relative bargaining power of firms and laborers with higher θ indicating more firm bargaining power.
3. Model Results
When considering optimization at a particular period t, I omit the t subscripts for brevity. In addition, variables with a superscript * denote a Pareto optimal level for that variable.
If the intermediaries were to have perfect information about the firms’ activities and could raise capital for sufficiently low cost, then the level of output would be Pareto efficient, as intermediaries could extract all of the surplus from the firm. First, consider the bargaining problem between the firm and the laborer. Taking natural logs of the bargaining solution and letting μ denote a Lagrange multiplier, the Karush-Kuhn-Tucker Lagrangian can be written as Equation (5)4.
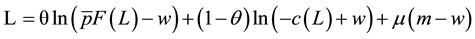 (5)
(5)
If the wage constraint does not bind, then firms and laborers trade optimally and the outcome is Pareto efficient. The first order conditions at the maximum of Equation (5) are:
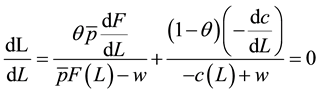 (6)
(6)
 (7)
(7)
which results in the optimal labor
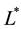 being traded.
being traded.
However, under imperfect information and costly capital accumulation, the constraint may bind (w = m) and the quantity of labor traded will be inefficiently low. Taking the first order condition of the Karush-Kuhn-Tucker Lagrangian in Equation (5) with respect to wage when the constraint binds yield Equation (8).
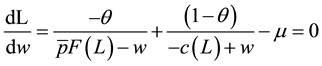 (8)
(8)
Substituting Equation (6) into Equation (8) and rearranging:
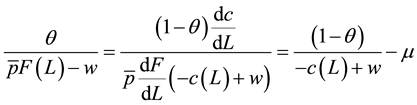 (9)
(9)
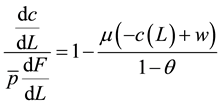 (10)
(10)
Because of the participation constraint
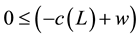 and bounds on
and bounds on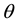 ,
,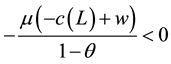 . Since
. Since
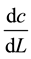 and
and
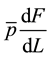 are both positive, when the wage constraint binds
are both positive, when the wage constraint binds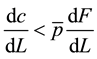 . Therefore, firms would be
. Therefore, firms would be
willing to hire more labor and households would want to supply more labor, which implies that the total surplus generated at this point is below the maximum amount, or that
Acknowledgements
The views expressed in this paper are mine and are not necessarily those of the Federal Reserve Board or the Federal Reserve System. I wish to thank Guillaume Rocheteau and an anonymous referee for helpful comments. I am responsible for any errors.
References
- Arrow, K.J. (1962) Economic Welfare and the Allocation of Resources for Invention. In: Nelson, R.R., Ed., The Rate and Direction of Inventive Activity, Princeton University Press, Princeton, 609-626.
- Hall, B.H. and Lerner, J. (2009) The Financing of R & D and Innovation. NBER Working Paper 15325.
- Allen, F. and Santomero, A.M. (2001) What Do Financial Intermediaries Do? Journal of Banking and Finance, 25, 271-294. http://dx.doi.org/10.1016/S0378-4266(99)00129-6
- Antunes, A., Cavalcanti, T. and Villamil, A. (2013) Costly Intermediation and Consumption Smoothing. Economic Inquiry, 51, 459-472. http://dx.doi.org/10.1111/j.1465-7295.2012.00471.x
- Nosal, E. and Rocheteau, G. (2011) A Search Approach to Money, Payments, and Liquidity. MIT Press, Cambridge.
- Beck, T., Demirg c-Kunt, A. and Levine, R. (2000) A New Database on the Structure and Development of the Financial Sector. World Bank Economic Review, 14, 271-294. http://dx.doi.org/10.1093/wber/14.3.597
NOTES

1See [6] for data on financial intermediation costs.
2In this context, θ represents the relative bargaining power of firms and laborers with higher θ indicating more firm bargaining power.
3Non-negativity constraints apply for all types of agents.

4The non-negativity conditions on w and L will always hold with the participation constraints on the firm and the laborer, so I omit them.

