Theoretical Economics Letters
Vol. 3 No. 5A1 (2013) , Article ID: 36267 , 9 pages DOI:10.4236/tel.2013.35A1005
Deforestation, Forest Fallowing, and Soil Conservation in Shifting Cultivation
Faculty of Humanities and Social Sciences, University of Tsukuba, Tsukuba, Japan
Email: takasaki@sk.tsukuba.ac.jp
Copyright © 2013 Yoshito Takasaki. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 21, 2013; revised July 21, 2013; accepted August 21, 2013
Keywords: Shifting Cultivation; Deforestation; Forest Fallowing; Soil Conservation
ABSTRACT
To design effective policies for rainforest conservation in shifting cultivation systems, it is crucial to have a better understanding of shifting cultivators’ decision making. This paper develops a unified dynamic farm model of shifting cultivation, addressing two lacunae in extant theoretical works: taking into account differences between primary and secondary forests and potential roles of on-farm soil conservation. The model unifies shifting cultivator’s decisions about primary-forest clearing, forest fallowing, and on-farm soil conservation by incorporating new soils acquired from cleared primary/secondary forest land into on-farm soil dynamics. I examine how three distinct policies—forest protection (e.g., protected areas), fallow management (e.g., improved fallow), and on-farm soil management (e.g., biochar in Amazonia)—alter primary-forest clearing (deforestation) and fallow length. The analysis reveals that although all three policies reduce deforestation, only on-farm soil management leads to longer fallow, i.e., sustainable secondary fallow forest.
1. Introduction
Shifting cultivation is a dominant agricultural system in tropical forests. Shifting cultivators transform nutrients stored in standing forests to soils by slashing, felling, and burning forests (i.e., slash-and-burn) [1,2]. Not only is shifting cultivation one of the major causes of deforestation and forest degradation, but also, the associated forest-cover change results in other environmental problems, such as soil degradation, biodiversity loss, and reduced carbon sequestration [1,3-6]. To design effective policies for rainforest conservation in shifting cultivation systems, having a better understanding of shifting cultivators’ decision making is crucial. This paper develops a new shifting-cultivation model to address two major lacunae in the literature [7].
First, extant theoretical works do not distinguish between primary and secondary forests1,2. In general, protecting primary forest with greater biodiversity needs to be given a higher priority than secondary forest protection. At the same time, as primary forest becomes scarce in the tropics, researchers and practitioners pay greater attention to secondary fallow forest.3 In particular, short fallow results in less matured secondary forest with limited biomass accumulation and poor protection of erodible soils, as well as low biodiversity, weak carbon sequestration, and limited timber and non-timber forest products [4-6,12,13].
The second lacuna is the investigation into potential roles of on-farm soil conservation. Among poor shifting cultivators, forest-based soil-management options—forest clearing and fallowing—outweigh on-farm soil conservation [14]. This is because when degraded land can be easily replaced, farmers have little incentive to adopt expensive, input-based soil-conservation measures. Although developing locally adoptable, effective on-farm soil-conservation measures in tropical forests has been a daunting task [15], soil scientists’ recent growing interest in biochar in Amazonia may lead to a significant improvement in soil fertility and soil carbon sequestration in shifting cultivation systems [16-19].4 At the same time, various management measures to improve fallows by planting species that replenish soil nutrient stocks faster than plants in natural succession are available and have been practiced across the tropics [20-22].5
To fill these two lacunae, the paper unifies shifting cultivator’s decisions about primary-forest clearing, forest fallowing, and on-farm soil conservation. I do so by extending the land-replacement-modeling approach, which explicitly captures shifting cultivators’ motive for clearing forests: to acquire new fertile soils [7,27]. As labor is a key scarce factor among shifting cultivators in land-abundant tropical environments [28], the model highlights the tradeoff in labor allocations associated with primary/secondary-forest clearing and on-farm soil management; cleared primary forest is more fertile than secondary forest land, but the former clearing is more labor intensive, and the alternative “slash-and-char” system is also labor intensive [29]. In particular, the model incorporates new soils acquired from cleared primary/ secondary forest land into on-farm soil dynamics. Although my model best reflects shifting cultivation practices among Amazonian peasants [10,11], the modeling framework can be widely applied to other shifting cultivation systems in the tropics.
This unified model allows me to examine how policies can alter shifting cultivators’ decisions about primaryforest clearing and fallow length, which determine the two key outcomes of rainforest conservation: protecting primary forest and maintaining sustainable secondary fallow forest which are keys for reducing emissions from deforestation and forest degradation (REDD) [30]. I compare three policies—soil management interventions for fallow and cultivated land, respectively, as discussed above, and forest-protection measures [31].6 Although many empirical studies show that protected areas can significantly reduce tropical deforestation [32-35], systematic empirical works on the roles of fallow and onfarm soil management for rainforest consevation in shifting cultivation systems are lacking. The comparative static analyses reveal that although not only forest protection but also fallow and on-farm soil management reduces deforestation in the long run, only on-farm soil management increases fallow length.
As is any theoretical model, my unified model is built on various assumptions (detailed below). In particular, a fixed land size is assumed. This assumption is restrictive, because cleared primary forest usually adds to land holdings [7]. Then, it is possible that better on-farm soil management encourages shifting cultivators to clear more primary forest to expand land holdings in response to increased returns to farming. The theoretical literature, however, has not yet fully integrated shifting-cultivation practices and land accumulation [11].7 The paper is a first attempt to model shifting cultivation in a way that addresses the two major lacunae in the literature discussed above; developing a more comprehensive model, especially one endogenizing land accumulation, is an important agenda for future research.
The rest of the paper is organized as follows. Section 2 develops the dynamic farm model, derives the optimal path of labor allocations, and characterizes the steadystate equilibrium. Section 3 conducts comparative static analyses on policy impacts. The last section concludes.
2. The Model
Let us consider a representative farmer who cultivates agricultural land with the size of 1. Let a and b (0 < a, b < 1, a + b < 1) denote the land that is replaced with newly cleared primary and secondary fallow forest lands, respectively. Cleared forests bring new soils. Secondary forest is less fertile but easier to clear than primary forest [37]. Primary-forest land is homogeneous in terms of soil fertility, and the soil stock per unit forest land is assumed to be 1, with no loss of generality. Contrarily, the fertility of secondary forest land is determined by fallow length [38]. Following Larson and Bromley [39], I assume a fixed land allocation between swidden and fallow. Then, the size of fallow forest land is written as θ(1 − a), where θ is the fixed ratio of fallow land to swidden land 1 − a. Fallow length N is given by θn, where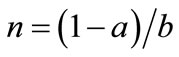 , i.e., the ratio of swidden land to the land switched between swidden and fallow (n > 1, because a + b < 1).8 Thus, fallow length is determined by both primaryand secondary-forest clearings: If both clearings diminish, fallow becomes longer; if the diminished and augmented clearings coexist, their net effect on fallow length is generally ambiguous. With a fixed θ, the fertility of fallow land is determined only by n: The fallow-land fertility per unit of land is
, i.e., the ratio of swidden land to the land switched between swidden and fallow (n > 1, because a + b < 1).8 Thus, fallow length is determined by both primaryand secondary-forest clearings: If both clearings diminish, fallow becomes longer; if the diminished and augmented clearings coexist, their net effect on fallow length is generally ambiguous. With a fixed θ, the fertility of fallow land is determined only by n: The fallow-land fertility per unit of land is , where k’ > 0, k” < 0, and η is a fixed productivity parameter of soil regeneration under natural fallow. ηk’ measures the rate of soil regeneration per unit of fallow length. Secondary fallow forest land never becomes more fertile than primary-forest land, i.e.,
, where k’ > 0, k” < 0, and η is a fixed productivity parameter of soil regeneration under natural fallow. ηk’ measures the rate of soil regeneration per unit of fallow length. Secondary fallow forest land never becomes more fertile than primary-forest land, i.e., .
.
The farmer’s soil regeneration technology on the cultivated land uses labor as a unique input [40,41]. Letting m denote the labor per unit land allocated to on-farm soil management, the total regenerated soil is a concave function of non-replaced land 1 − a − b and labor input on the non-replaced land m(1 − a − b). With a constant-returns-to-scale regeneration function, the total regenerated soil is written as αh(m)(1 − a − b), where αh(m) is the regenerated soil per unit land, such that ,
, 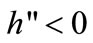 , and α is a fixed productivity parameter of on-farm soil regeneration. The regenerated soil on the non-replaced land never becomes more fertile than primary forest land, i.e.,
, and α is a fixed productivity parameter of on-farm soil regeneration. The regenerated soil on the non-replaced land never becomes more fertile than primary forest land, i.e.,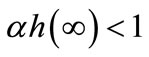 . The farmer’s cultivation intensity also affects soil dynamics; the more labor-intensive the cultivation, the more soil is lost. Total soil loss is given by βl, where l is labor allocated to cultivation and β is constant soil loss per unit of cultivation labor.
. The farmer’s cultivation intensity also affects soil dynamics; the more labor-intensive the cultivation, the more soil is lost. Total soil loss is given by βl, where l is labor allocated to cultivation and β is constant soil loss per unit of cultivation labor.
An example of the fertility profile across plots (for given a and b) is depicted by the solid line ABCDEF in Figure 1, where each plot is displayed in the decreasing order of fertility. The total soil stock x, the area below ABCDEF, consists of a on the newly cleared primary forest land OG, ηkb on the cleared secondary forest land GH, and the soil on the remaining plots HK. The fertility profile after cultivation and the replacement and abandonment of the infertile plots IJ and JK, respectively, is depicted by the broken line LM9. The area between ABCDEF and LMIK is total soil loss resulting from cultivation βl. The revised fertility profile of OI after regeneration is given by the dotted line NP (LM has shifted upward by αh). In the next cultivation, NP becomes old plots and shifts rightward by a + b (at a steady state, NP and EF are the same). Hence, the evolution of soil stock x on the farm land is written as10:

Figure 1. Soil fertility profile across plots.
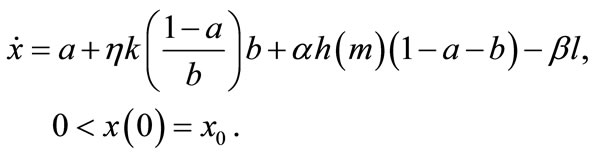 (1)
(1)
The farmer acquires new soil a and loses regenerated soils on the abandoned plots . Thus, 1 − αh(m), which is positive, represents the net soil addition per unit crop land through primary-forest clearing. Similarly,
. Thus, 1 − αh(m), which is positive, represents the net soil addition per unit crop land through primary-forest clearing. Similarly,  captures the net soil addition through secondary-forest clearing, which is also shown to be positive below.
captures the net soil addition through secondary-forest clearing, which is also shown to be positive below.
The following three assumptions are made. First, primary forest is locally abundant, open-access, and unmanaged. Thus, forest stock is exogenous to the private farmer. This institutional setup, which is common in the deforestation literature [7,42,43], applies to many tropical areas, especially those where rapid deforestation is an emergency problem, as in Amazonia. Second, all cleared lands, both farm land and fallow land, are secure under customary tenure (usufruct). This institutional setup applies to peasants and indigenous populations in Amazonia11. Third, the farmer earns no income from standing primary and secondary forests in the form of non-timber forest products. Because to add such earning options would augment the benefit of maintaining standing forests, the present model ignoring them is considered to be “conservative” in the study of forest clearing.12
With the fixed amount of primary forest land, more forest clearing requires longer travel for clearing. Labor required to clear a primary forest land is given by πs(a)where s(0) = 0, 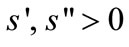 , and a fixed parameter π increases as the per-capita stock of primary forest declines (e.g., through the establishment of protected areas). A linear clearing function is assumed for secondary fallow forest with the proximity to the farmer’s plots: The farmer allocates τb labor to clear b secondary forest, where τ is a fixed marginal labor cost, which is always smaller than that of primary-forest clearing, i.e., τ < πs’(0).13
, and a fixed parameter π increases as the per-capita stock of primary forest declines (e.g., through the establishment of protected areas). A linear clearing function is assumed for secondary fallow forest with the proximity to the farmer’s plots: The farmer allocates τb labor to clear b secondary forest, where τ is a fixed marginal labor cost, which is always smaller than that of primary-forest clearing, i.e., τ < πs’(0).13
The farmer’s crop output is a function of soil stock and cultivation labor,  , where f(0,l) = f(x,0) = 0, fx, fl > 0, fxx, fll < 0, and fxl ≥ 0 (the subscripts represent derivatives in a standard manner). Concavity is guaranteed by the non-negativity of the determinant of the Hessian matrix of f, i.e.,
, where f(0,l) = f(x,0) = 0, fx, fl > 0, fxx, fll < 0, and fxl ≥ 0 (the subscripts represent derivatives in a standard manner). Concavity is guaranteed by the non-negativity of the determinant of the Hessian matrix of f, i.e.,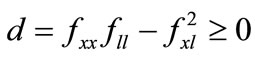 . The farmer hires labor lh at a fixed wage w in a perfect labor market, and alternatively, the negative lh means that he/she sells labor14. The farmer’s labor time constraint is
. The farmer hires labor lh at a fixed wage w in a perfect labor market, and alternatively, the negative lh means that he/she sells labor14. The farmer’s labor time constraint is
 (2)
(2)
where L is his/her time endowment. With a perfect labor market, the farmer’s utility maximization is recursive: The farmer maximizes the profit first [51].
The farmer chooses cultivation labor, soil conservation labor, and secondaryand primary-forest clearing over time to maximize his/her discounted total profits:
 (1), (2)where p is a fixed crop price and r is a fixed discount rate (risk is ignored). The current-value Hamiltonian is given by
(1), (2)where p is a fixed crop price and r is a fixed discount rate (risk is ignored). The current-value Hamiltonian is given by

where λ is the current-value costate variable for soil stock.
Given an internal solution, the first-order necessary conditions for optimality are (1) plus the following:
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
Equation (3) indicates that farming labor is chosen to the point where the value of the marginal product of labor equals wage, plus the marginal value of soil loss resulting from cultivation. Equation (4) suggests that soil conservation labor is chosen to the extent that the value of the marginal product of on-farm soil regeneration equals forgone wage. In Equation (5), secondary fallow forest is cleared to the extent that the value of net soil addition, plus the saved wage through a reduction in soil conservation labor (more intensive secondary-forest clearing involves more land replacement), equals the forgone wage through clearing, plus the value of the forgone marginal soil regeneration on the fallow land through shortened fallow. The interpretation of Equation (6) with respect to primary-forest clearing is analogous. Equation (7) is the standard costate condition, giving the optimal evolution of the shadow value of soil stock. Transversality conditions are given by Equation (8). Because the Hamiltonian is jointly concave in the state and control variables, these necessary conditions are sufficient for optimality15.
The steady-state equilibrium, the existence of which is assumed, is shown to be unique and stable, as follows. The steady-state equilibrium (x*, λ*) is given by  in Equations (1) and (7), and once the steady-state values for x* and λ* are known, those for l*, m*, b*, and a* are obtained recursively from (3)-(6). Substituting l, m, b, and a from Equations (3)-(6), the canonical system is expressed by (1) and (7). Linearising the system at the steady state yields the following Jacobian matrix:
in Equations (1) and (7), and once the steady-state values for x* and λ* are known, those for l*, m*, b*, and a* are obtained recursively from (3)-(6). Substituting l, m, b, and a from Equations (3)-(6), the canonical system is expressed by (1) and (7). Linearising the system at the steady state yields the following Jacobian matrix:

where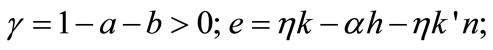 φ = 1 − αh − (k − αh)n−1 > 0;
φ = 1 − αh − (k − αh)n−1 > 0; ,
,  , and J21 ≥ 0, where Jmn is the (m, n) factor of matrix J. Because the
, and J21 ≥ 0, where Jmn is the (m, n) factor of matrix J. Because the 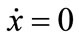 and
and  loci, respectively, are upward and downward sloping in the λ-x space, the equilibrium (x*λ*), which is determined as their intersection, is unique. Because
loci, respectively, are upward and downward sloping in the λ-x space, the equilibrium (x*λ*), which is determined as their intersection, is unique. Because 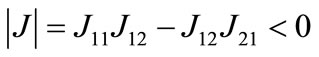 and
and 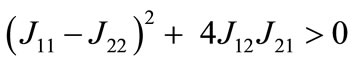 , both characteristic roots are real and have opposite signs, and thus the equilibrium is stable as a saddle point [54].
, both characteristic roots are real and have opposite signs, and thus the equilibrium is stable as a saddle point [54].
3. Policy Analysis
The comparative statics of l*, m*, b*, a*, and x* with respect to exogenous variables can be obtained from Equations (3), (5), (6), (1), and (7) with the substitution of λ from (4). The determinant of the Hessian matrix of the system of these five equations is given by:
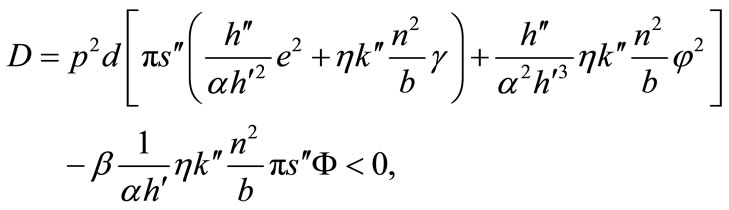
where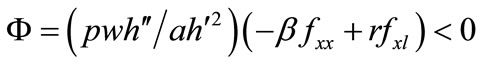 . Secondaryforest-clearing labor is assumed to be greater than soilconservation labor, i.e., τ > m; then, e > 0 (see Equation (5)).
. Secondaryforest-clearing labor is assumed to be greater than soilconservation labor, i.e., τ > m; then, e > 0 (see Equation (5)).
I consider three policies: 1) forest protection (higher π); 2) improved fallow to augment soil regeneration under fallow (higher η); and 3) on-farm soil management to augment soil regeneration on non-replaced cultivated land (higher α). Key outcome measures are primary-forest clearing a* and fallow length N* in the long run (the asterisks represent the steady-state equilibrium). With a fixed θ, effects on N* are qualitatively the same as those on . To facilitate interpretations, soil conservation labor m* is also examined.
. To facilitate interpretations, soil conservation labor m* is also examined.
The comparative statics are reported in Table 1. Many results of the two soil management measures, but not forest protection, depend on farming technology: Many results are ambiguous when d > 0, but most ambiguities vanish when d = 0. This is because for the latter technologies, all adjustments in Equations (3) and (7) are determined by the shadow value of soil stock, which unambiguously increases with augmented soil conservation labor (see Equation (4)), because adjustments in cultivation labor and soil stock cancel each other out (note that no other endogenous variables appear in Equations (3) and (7)). With d > 0, this neutrality of farming technology vanishes because of the adjustments in crop production. Many empirical works that estimate the production functions of shifting cultivation employ a CobbDouglas technology, for which d = 0 [55-57]. The summary of the comparative static results in Table 2 is based on those with d = 0 for soil-management measures; those for forest protection do not depend on the sign of d.
First, forest protection always reduces and increases primaryand secondary-forest clearing, respectively. As the former becomes more costly than the latter, this shift


Table 1. Comparative statics.
is an obvious result of substitution. Although these two impacts counteract each other in determining fallow length, the secondary-forest effect always outweighs the primary-forest effect, resulting in shorter fallow. Thus, protecting primary forest involves less sustainable secondary forest as a tradeoff. In contrast, soil-conservation labor input is always augmented. This is because the farmer offsets a decrease in the acquisition of fertile soil from primary forest land, which is greater in magnitude than an increase in the acquisition of less fertile soil (as a result of shortened fallow) from secondary forest land.
Second, the results for improved fallow are qualitatively the same as those for forest protection. Secondary forest is substituted for primary forest in the farmer’s soil management portfolio, as follows. On one hand, primary-forest clearing is reduced, because with higher η, its marginal cost ηk’—reduced soil regeneration under fallow—increases more than its benefit (see Equation

Table 2. Summary of comparative static results.
(6)). On the other hand, secondary-forest clearing is augmented, because higher η increases fallow soil minus the forgone marginal soil regeneration on the fallow land, ηk − ηk’n (≡ g > 0 because e > 0) (see Equation (5)). As the latter effect unambiguously outweighs the former, fallow always becomes shorter. To offset the balance of these two forest-based soil managements, on-farm soil management is intensified. Shortened fallow is not surprising at all, because this policy speeds up the soil regeneration. The question is whether or not the fertility of fallow land ηk(n) is improved. Although d(ηk(n))/dη = k(n) + ηk’(n)dn/dη is generally unsigned even if d = 0, this comparative statics is likely to be positive, unless fallow length n becomes very short. Whether and how much this policy mitigates adverse ecological impacts of short fallow discussed above are empirical questions, the answers to which depend on specific fallow-management measures. As such, although improved fallow protects primary forest, it may do so at the cost of unsustainable secondary-fallow forest.
Third, enhanced on-farm soil regeneration always leads to the intensification of on-farm soil management and thus more fertile soil on the cultivated land αh(m). It also unambiguously reduces primary-forest clearing, because the net soil addition on crop land through primary-forest clearing (1 − αh) decreases. In contrast, the impacts on secondary-forest clearing are indeterminate even if d = 0, because the net soil addition through secondary-forest clearing (ηk − αh) is ambiguously altered, depending on fallow length. Fallow unambiguously becomes longer, because the former primary-forest effect always outweighs the latter secondary-forest effect. An important difference of this policy from the other two policies is that although the latter two directly affect either one of the two forest-based soil management options —primaryor secondary-forest clearing, the former alters the benefit-cost comparisons of the on-farm option with both of them16.
4. Conclusion
This paper developed a unified dynamic farm model of primary-forest clearing, forest fallowing, and on-farm soil conservation in shifting cultivation by incorporating new soils acquired from cleared primary/secondary forest land into on-farm soil dynamics. The comparative static analysis revealed that although forest protection (e.g., protected areas), fallow management (e.g., improved fallow), and on-farm soil management (e.g., biochar in Amazonia) all reduce primary-forest clearing (deforestation) in the long run, only on-farm soil management increases fallow length. A caveat is that the model ignores land accumulation; with an additional motive for clearing primary forest—land expansion—better on-farm soil management instead may lead to augmented deforestation. Then, to attain the win-win goal of protecting primary forest and maintaining sustainable secondary fallow forest (longer fallow), an effective policy mix is needed. These promising findings of the paper call for new empirical studies on the roles of fallow and on-farm soil management for rainforest conservation in shifting cultivation systems.
5. Acknowledgements
An earlier draft of this paper benefited significantly from the suggestions of Brad Barham, Michael Carter, JeanPaul Chavas, Oliver Coomes, and Bill Provencher. I gratefully acknowledge the generous financial support of my research by the following organizations: Foundation for Advanced Studies on International Development, the Mellon Foundation, the Institute for the Study of World Politics, the MacArthur Foundation, the Graduate School of the University of Wisconsin-Madison, the Matsushita International Foundation, Japan Society for the Promotion of Science, and Ministry of Education, Culture, Sports, Science and Technology in Japan. Any errors of interpretation are solely the author’s responsibility.
REFERENCES
- P. J. A. Kleinman, D. Pimentel and R. B. Bryant, “The Ecological Sustainability of Slash-and-Burn Agriculture,” Agriculture, Ecosystems and Environment, Vol. 52, No. 2-3, 1995, pp. 235-249. doi:10.1016/0167-8809(94)00531-I
- H. Ruthenberg, “Farming Systems in the Tropics,” 3rd Edition, Clarendon Press, Oxford, 1980.
- N. Myers, “The Primary Source: Tropical Forests and Our Future,” W. W. Norton, New York, 1992.
- D. Lawrence, V. Suma and J. P. Mogea, “Changes in Species Composition with Repeated Shifting Cultivation: Limited Role of Soil Nutrients,” Ecological Applications, Vol. 15, No. 6, 2005, pp. 1953-1967. doi:10.1890/04-0841
- R. L. Chazdon, C. A. Peres, D. Dent, D. Sheil, A. E. Lugo, D. Lamb, N. E. Stork and S. E. Miller, “The Potential for Species Conservation in Tropical Secondary Forests,” Conservation Biology, Vol. 23, No. 6, 2009, pp. 1406- 1417. doi:10.1111/j.1523-1739.2009.01338.x
- D. H. Dent and S. J. Wright, “The Future of Tropical Species in Secondary Forests: A Quantitative Review,” Biological Conservation, Vol. 142, No. 12, 2009, pp. 2833- 2843. doi:10.1016/j.biocon.2009.05.035
- Y. Takasaki, “Economic Models of Shifting Cultivation: A Review,” In: P. Moutinho, Ed., Deforestation around the World, InTech, Rijeka, 2012, pp. 351-372. doi:10.5772/35745
- J. Smith, P. van de Kop, K. Reategui, I. Lombardi, C. Sabogal and A. Diaz, “Dynamics of Secondary Forests in Slash-And-Burn Farming: Interactions among Land Use Types in the Peruvian Amazon,” Agriculture Ecosystems & Environment, Vol. 76, No. 2-3, 1999, pp. 85-98. doi:10.1016/S0167-8809(99)00075-4
- L. H. Pendleton and E. L. Howe, “Market Integration, Development, and Smallholder Forest Clearance,” Land Economics, Vol. 78, No. 1, 2002, pp. 1-19. doi:10.2307/3146919
- O. T. Coomes, F. Grimard and G. J. Burt, “Tropical Forests and Shifting Cultivation: Secondary Forest Fallow Dynamics among Traditional Farmers of the Peruvian Amazon,” Ecological Economics, Vol. 32, No. 1, 2000, pp. 109-124. doi:10.1016/S0921-8009(99)00066-X
- O. T. Coomes, Y. Takasaki and J. Rhemtulla, “Land-Use Poverty Traps Identified in Shifting Cultivation Systems Shape Long-Term Tropical Forest Cover,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 108, No. 34, 2011, pp. 13925-13930. doi:10.1073/pnas.1012973108
- S. Brown and A. E. Lugo, “Tropical Secondary Forests,” Journal of Tropical Ecology, Vol. 6, No. 1, 1990, pp. 1- 32. doi:10.1017/S0266467400003989
- S. P. Dalle and S. de Bois, “Shorter Fallow Cycles Affect the Availability of Noncrop Plant Resources in a Shifting Cultivation System,” Ecology and Society, Vol. 11, No. 2, 2006, p. 2.
- E. B. Barbier, “The Economic Determinants of Land Degradation in Developing Countries,” Philosophical Transactions of the Royal Society of London: Series B, Vol. 352, No. 1356, 1997, pp. 891-899.
- R. Lal, “Sustainable Management of Soil Resources in the Humid Tropics,” United Nations University Press, Tokyo, 1995.
- B. Glaser, “Ameliorating Physical and Chemical Properties of Highly Weathered Soils in the Tropics with Charcoal—Review,” Biology and Fertility of Soils, Vol. 354, No. 4, 2002, pp. 219-230. doi:10.1007/s00374-002-0466-4
- B. Glaser, “Prehistorically Modified Soils of Central Amazonia: A Model for Sustainable Agriculture in the Twenty-First Century,” Philosophical Transactions of the Royal Society B, Vol. 362, No. 1478, 2007, pp. 187-196. doi:10.1098/rstb.2006.1978
- E. Marris, “Putting the Carbon Back: Black is the New Green,” Nature, Vol. 442, No. 7103, 2006, pp. 624-626. doi:10.1038/442624a
- C. Steiner, W. G. Teixeira and W. Zech, “Slash and Char: An Alternative to Slash and Burn Practiced in the Amazon Basin,” In: J. Lehman, D. C. Kern, B. Glaser and J. Woods, Eds., Amazonian Dark Earths: Origins, Properties, and Management, Kluwer Academic Publishers, Dordrecht, 2004, pp. 125-139.
- P. A. Sanchez, “Science in Agroforestry,” Agroforestry Systems, Vol. 30, No. 1-2, 1995, pp. 5-55. doi:10.1007/BF00708912
- P. A. Sanchez, “Improved Fallows Come of Age in the Tropics,” Agroforestry Systems, Vol. 47, No. 1-3, 1999, pp. 3-12. doi:10.1023/A:1006287702265
- A. Young, “Agroforestry for Soil Management,” CAB International and ICRAF, New York, 1997.
- H. Brookfield and C. Padoch, “Appreciating Agrodiversity: A Look at the Dynamism and Diversity of Indigenous Farming Practices,” Environment, Vol. 36, No. 5, 1994, pp. 6-11, 37-45. doi:10.1080/00139157.1994.9929164
- W. M. Denevan and C. Padoch, “Swidden-Fallow Agroforestry in the Peruvian Amazon,” The New York Botanical Garden, Bronx, 1987.
- J. D. Unruh, “Ecological Aspects of Site Recovery under Swidden-Fallow Management in the Peruvian Amazon,” Agroforestry Systems, Vol. 7, No. 2, 1988, pp. 161-184. doi:10.1007/BF00046850
- R. D. C. G. Mesquita, “Management of Advanced Regeneration in Secondary Forests of the Brazilian Amazon,” Forest Ecology and Management, Vol. 130, No. 1-3, 2000, pp. 131-140. doi:10.1016/S0378-1127(99)00174-7
- Y. Takasaki, “A Model of Shifting Cultivation: Can Soil Conservation Reduce Deforestation?” Agricultural Economics, Vol. 35, No. 2, 2006, pp. 193-201. doi:10.1111/j.1574-0862.2006.00152.x
- Y. Takasaki, O. T. Coomes, C. Abizaid and S. Brisson, “An Efficient Nonmarket Institution under Imperfect Markets: Labor Sharing for Tropical Forest Clearing,” American Journal of Agricultural Economics, in Press.
- S. N. Swami, C. Steiner, W. G. Teixeira and J. Lehmann, “Charcoal Making in the Brazilian Amazon: Economic Aspects of Production and Carbon Conversion Efficiencies of Kilns,” In: W. I. Woods, Ed., Amazonian Dark Earths: Wim Sombroek’s Vision, Springer, Heidelberg, 2009, pp. 411-422. doi:10.1007/978-1-4020-9031-8_23
- A. Angelsen, “Moving Ahead with REDD: Issues, Options and Implications,” Center for International Forestry Research, Bogor, 2008.
- Millennium Ecosystem Assessment, “Ecosystems and Human Well-Being: Policy Response,” Island Press, Washington, D.C., 2005.
- K. Andam, P. J. Ferraro, A. Pfaff, A. Sanchez-Azofeifa and J. Robalino, “Measuring the Effectiveness of Protected Area Networks in Reducing Deforestation,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 105, No. 42, 2008, pp. 16089- 16094. doi:10.1073/pnas.0800437105
- L. Naughton-Treves, M. B. Holland and K. Brandon, “The Role of Protected Areas in Conserving Biodiversity and Sustaining Local Livelihoods,” Annual Review of Environment and Resource Economics, Vol. 30, No. 1, 2005, pp. 219-252. doi:10.1146/annurev.energy.30.050504.164507
- P. J. C. Olivera, G. P. Asner, D. E. Knapp, A. Almeyda, R. Galván-Gildemeister, S. Keene, R. F. Raybin and R. C. Smith, “Land-Use Allocation Protects the Peruvian Amazon,” Science, Vol. 317, No. 5842, 2007, pp. 1233-1236. doi:10.1126/science.1146324
- A. G. Bruner, R. E. Gullison, R. R. E. and G. A. B. Da Fonseca, “Effectiveness of Parks in Protecting Tropical Biodiversity,” Science, Vol. 291, No. 5501, 2001, pp. 125-128. doi:10.1126/science.291.5501.125
- T. Tachibana, T. M. Nguyen and K. Otsuka, “Agricultural Intensification versus Extensification: A Case Study of Deforestation in the Northern-Hill Region of Vietnam,” Journal of Environmental Economics and Management, Vol. 41, No. 1, 2001, pp. 44-69. doi:10.1006/jeem.1998.1131
- F. N. Scatena, R. T. Walker, A. K. O. Homma, A. de Conto, C. A. P. Ferreira, R. D. A. Carvalho, A. C. P. N. de Rocha, A. I. M. dos Santos and P. M. de Oliverira, “Cropping and Fallowing Sequences of Small Farmers in the ‘Terra Firme’ Landscape of the Brazilian Amazon: A Case Study from Santarem, Para,” Ecological Economics, Vol. 18, No. 1, 1996, pp. 29-40. doi:10.1016/0921-8009(95)00055-0
- K. A. Dvořàk, “Resource Management by West African Farmers and the Economics of Shifting Cultivation,” American Journal of Agricultural Economics, Vol. 74, No. 3, 1992, pp. 809-815. doi:10.2307/1242600
- B. A. Larson and D. W. Bromley, “Property Rights, Externalities, and Resource Degradation,” Journal of Development Economics, Vol. 33, No. 2, 1990, pp. 235-262. doi:10.1016/0304-3878(90)90023-5
- E. H. Bulte and D. P. van Soest, “A Note on Soil Depth, Failing Markets and Agricultural Pricing,” Journal of Development Economics, Vol. 58, No. 1, 1999, pp. 245- 254. doi:10.1016/S0304-3878(98)00111-4
- E. H. Bulte and D. P. van Soest, “Environmental Degradation in Developing Countries: Households and the (Reverse) Environmental Kuznets Curve,” Journal of Development Economics, Vol. 65, No. 1, 2001, pp. 225- 235. doi:10.1016/S0304-3878(01)00135-3
- D. Kaimowitz and A. Angelsen, “Economic Models of Tropical Deforestation: A Review,” Center for International Forestry Research, Bogor, 1998.
- E. B. Barbier and J. C. Burgess, “The Economics of Tropical Deforestation,” Journal of Economic Surveys, Vol. 15, No. 3, 2001, pp. 413-433. doi:10.1111/1467-6419.00144
- F. Place and K. Otsuka, “Population, Tenure, and Natural Resource Management: The Case of Customary Land Area in Malawi,” Journal of Environmental Economics and Management, Vol. 41, No. 1, 2001, pp. 13-32. doi:10.1006/jeem.2000.1134
- K. Otsuka and F. Place, “Land Tenure and Natural Resource Management,” The Johns Hopkins University Press, Baltimore and London, 2001.
- L. J. Alston, G. D. Libecap and B. Mueller, “Land Reform Policies, the Sources of Violent Conflict, and Implications for Deforestation in the Brazilian Amazon,” Journal of Environmental Economics and Management, Vol. 39, No. 2, 2000, pp. 162-188. doi:10.1006/jeem.1999.1103
- T. L. Anderson and P. J. Hill, “The Race for Property Rights,” Journal of Law and Economics, Vol. 33, No. 1, 1990, pp. 177-197. doi:10.1086/467203
- L. Hotte, “Conflicts over Property Rights and NaturalResource Exploitation at the Frontier,” Journal of Development Economics, Vol. 66, No. 1, 2001, pp. 1-21. doi:10.1016/S0304-3878(01)00153-5
- B. Mueller, “Property Rights and the Evolution of a Frontier,” Land Economics, Vol. 73, No. 1, 1997, pp. 42-57. doi:10.2307/3147076
- D. Benjamin, “Household Composition, Labor Markets and Labor Demand: Testing for Separation in Agricultural Household Models,” Econometrica, Vol. 60, No. 2, 1992, pp. 287-322. doi:10.2307/2951598
- I. Singh, L. Squire and J. Strauss, “Agricultural Household Models: Extensions, Applications, and Policy,” The John Hopkins University Press, Baltimore, 1986.
- Y. Takasaki, “Dynamic Household Models of Forest Clearing under Distinct Land and Labor Market Institutions: Can Agricultural Policies Reduce Tropical Deforestation?” Environment and Development Economics, Vol. 12, No. 3, 2007, pp. 423-443. doi:10.1017/S1355770X07003567
- D. P. van Soest, E. H. Bulte, A. Angelsen and G. C. van Kooten, “Technological Change and Tropical Deforestation: A Perspective at the Household Level,” Environment and Development Economics, Vol. 7, No. 2, 2002, pp. 269-280.
- A. Seietstad and K. Sydsaeter, “Optimal Control Theory with Economic Applications,” Elsevier, Amsterdam, 1987.
- H. Klemick, “Shifting Cultivation, Forest Fallow, and Externalities in Ecosystem Services: Evidence from the Eastern Amazon,” Journal of Environmental Economics and Management, Vol. 61, No. 1, 2011, pp. 95-106. doi:10.1016/j.jeem.2010.07.003
- R. López, “Environmental Externalities in Traditional Agriculture and the Impact of Trade Liberalization: The Case of Ghana,” Journal of Development Economics, Vol. 53, No. 1, 1997, pp. 17-39. doi:10.1016/S0304-3878(97)00015-1
- U. Pascual, “Land Use Intensification Potential in Slashand-Burn Farming through Improvements in Technical Efficiency,” Ecological Economics, Vol. 52, No. 4, 2005, pp. 497-511.
NOTES
1Primary forest “has had little or no anthropogenic intervention,” and secondary forest is “woody successional vegetation that regenerates after the original forest cover has been removed for agriculture or cattle ranching” [8, p. 86].
2As an exception, Pendleton and Howe [9] address making the choice between primary and secondary forests as a pure forest-clearing problem; they neither model the role of secondary fallow forest as a soil builder nor consider soil addition through primary-forest clearing.
3Smith et al. [8] show that the relative importance of secondary forest to primary forest increased over time among Amazonian colonists. Coomes, Grimard and Burt [10] and Coomes, Takasaki and Rhemtulla [11] also find this pattern over a longer time span among Amazonian peasants (in their study village in Peru, primary forest has virtually disappeared).
4Biochar, also known as black carbon, is the residue of organic matter that has been pyrolyzed (partially combusted in a low-oxygen environment). Research indicates that Amazonian black carbon (terra preta) has, on average, three times more soil organic-matter content, higher nutrient levels, and a better nutrient retention capacity than surrounding infertile soils [17].
5Enriched fallows, which involve planting tree species with economic benefits (e.g., fruits, medicines) [23,24], may also enhance nutrient recovery, as shown by Unruh [25] in the Peruvian Amazon. An alternative approach to speed up soil regeneration under fallow is to accelerate secondary forest regrowth, for example, by canopy removal [26].
6Although protecting primary forest as the common often faces enforcement problems in practice, such problems are much smaller in the incentive-compatible measures affecting shifting-cultivators’ management of soils as their private asset.
7Although Tachibana, Nguyen and Otsuka [36] endogenize the evolution of upland holdings among Vietnamese farmers who combine upland shifting cultivation and lowland paddy cultivation, they do not distinguish or specify the type of cleared forest.
8For example, if θ = 5, a = 1/4, and b = 1/3, then n = 3 and N = 15.
9The remaining soils on the replaced and abandoned plots (which are not specified in Figure 1) do not affect the soil dynamics on the farm land. In particular, it is assumed that 1) the former soil stock does not affect the fertility of fallow forest, or the soil on the former land is used up before replacement, and 2) the latter plot is not added to fallow land (i.e., θ is unaltered).
10A perfect substitutability between regenerated soils through fallow and on-farm management is assumed; in particular, the nutrient accumulation process in these two is assumed not to be substantially different from each other. This assumption is consistent with biochar in Amazonia [17-19].
11In practice, however, the customary tenure of fallow land can be insecure, and this tenure insecurity influences shifting cultivators’ forest clearing and fallowing decisions [36,44,45]. Conflicts over property rights are common among colonists in the forest frontier [46- 49].
12Among Amazonian colonists, Smith et al. [8] find that secondary forest management is determined primarily by soil regeneration considerations and is unaffected by such forest products; farmers regard those products as “a bonus obtained during the fallow period”.
13The more matured the secondary fallow forest, the more labor is needed for clearing. Assuming that τ is positively related to fallow length does not alter the main results.
14Wage represents the opportunity cost of labor in the form of returns to any non-farm activities [50]. Although with a perfect labor market a market price (wage) supports a separation of a farm household’s consumption (labor supply) and production (labor demand) decisions, market imperfection can break this separation [51], often giving rise to ambiguous policy impacts on its decisions [52,53]. In contrast, examining Amazonian peasants’ forest clearing in Peru, Takasaki et al. [28] find that not only is their labor allocation efficient, as hired labor is combined with labor sharing, but also, family, hired, and shared labor are perfect substitutes for each other. This buttresses the assumption of labor-market perfection, which is common in extant theoretical works [7].
15Considering corner solutions is a straightforward extension. In particular, if a = 0, i.e., no primary-forest clearing, for example, in highly deforested areas, Equation (6) is irrelevant.
16I also examine impacts of output price and wage, which can be altered by a variety of macroeconomic policies, such as price subsidies, exchange-rate policies, and trade policies; alternatively, a higher p captures Hicks neutral technological progress in farming. Standard results are obtained: Regardless of the sign on d, promoting non-agricultural activities (higher w) always reduces primary-forest clearing and soil-conservation labor (and thus on-farm soil regeneration) and increases fallow length, as they discourage farming itself (the impact on secondary-forest clearing is ambiguous); the converse holds true for promoting agriculture (higher p).

