Theoretical Economics Letters
Vol. 3 No. 3A (2013) , Article ID: 33213 , 7 pages DOI:10.4236/tel.2013.33A005
Estimating Probability Distribution of Asset Value Based on Dual Effects of Deposit Insurance with the Minimum Cross-Entropy Principle
1Faculty of Management and Economics, Dalian University of Technology, Dalian, China
2School of Mathematics, Liaoning Normal University, Dalian, China
Email: seekyou77@hotmail.com, qinxz@dlut.edu.cn, 515937392@qq.com
Copyright © 2013 Xiaoning Lv et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 9, 2013; revised May 9, 2013; accepted June 9, 2013
Keywords: Probability Distribution; Deposit Insurance; Dual Effects; Cross-Entropy
ABSTRACT
A model is proposed to estimate the probability distribution of asset value based on the benefit effects as well as the risk effects of deposit insurance with the minimum cross-entropy principle. Three scenarios are constructed to depict situations with different dual effects of deposit insurance. The corresponding assets distribution functions are obtained accordingly. The results show that it is positively correlated between the supervision level and the risk aversion effects of deposit insurance. The increase of the deposit insurance premium moves the bank’s assets distribution to the right side although not significantly. The asset probability distributions estimated in this paper can be taken as a reference for banks to choose the proper credit investment projects.
1. Introduction
Deposit insurance is generally considered as an important institutional arrangement for the stability of the banking system. Currently more than 90 countries and regions around the world have established deposit insurance system. The recent crisis occurred in 2008 made 165 banks go bankrupt in the United States, which involves total deposits of 318.9 billion dollars. The federal deposit insurance corporation (FDIC) had played a positive role in a series of important crisis disposal process. To strengthen the depositors’ confidence, many counties chose to increase the coverage of deposit insurance during the crisis period. On one hand, the financial institutions may benefit from deposit insurance for the reduction of operational risk, on the other hand, they have the motive to increase the credit risk after taking deposit insurance, which may bring more threats to the financial system (See [1,2]). Therefore, it is worth concerning with the above dual effects of deposit insurance.
Several researches are engaged in the area of the dual effects of deposit insurance. Reference [3] discusses the microeconomic effects of deposit insurance during financial crisis. The results suggest that the increase of deposit insurance coverage helped to prevent a more serious and dangerous meltdown of deposits. Reference [4] finds that deposit insurance is partially effective in preventing bank runs by using minute-by-minute depositor withdrawal data. In recent years, with the outbreak and spread of the financial crisis, the limitation of deposit insurance system is gradually highlighting. For example, the “moral hazard” problem induced by deposit insurance could further aggravate the risk of the financial system. Accordingly, more and more scholars pay close attention to the risk effects of deposit insurance. The conclusions, however, are inconsistent among different researches that use diverse samples and methods. The empirical results do not support the existence of the risk effects of deposit insurance for the sample given in [5]. While [6] gives the opposite conclusion that deposit insurance significantly increases the credit risk of financial institutions. In fact, the benefit effects and the risk effects of deposit insurance may exist in the same time. By empirically analyzing the dual effects of deposit insurance, reference [7] finds that deposit insurance can effectively improve the efficiency of financial system and has a significant risk effects too.
Most of the researches aim at the results analysis on the dual effects of deposit insurance. The fact is that deposit insurance influences the probability distribution of the insured institution’s assets value at the first place and then engenders the dual effects. Therefore, it is important to properly estimate the assets distribution taking the deposit insurance into account. The minimum cross-entropy principle offers a method to implement distribution estimation considering some known information (See [8]). This paper tries to estimate the probability distribution of the insured institution’s assets value based on the dual effects of deposit insurance with the minimum cross-entropy principle.
The rest of the paper proceeds as follows. Section 2 presents the main method and the related calculations. Section 3 analyzes the simulation results. Section 4 draws a conclusion.
2. Methodology
2.1. Minimum Cross-Entropy
Definition 2.1. Two probability distributions F and G are defined on the probability space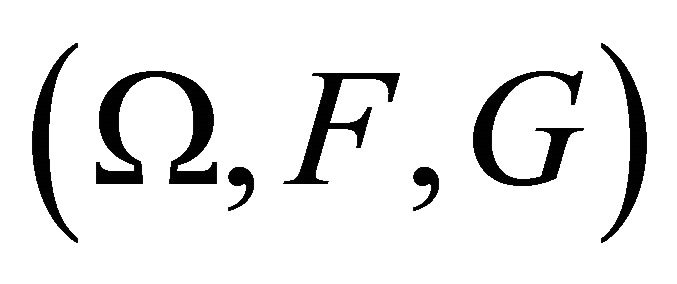 . The corresponding density functions are f and g, respectively. The cross-entropy,
. The corresponding density functions are f and g, respectively. The cross-entropy, 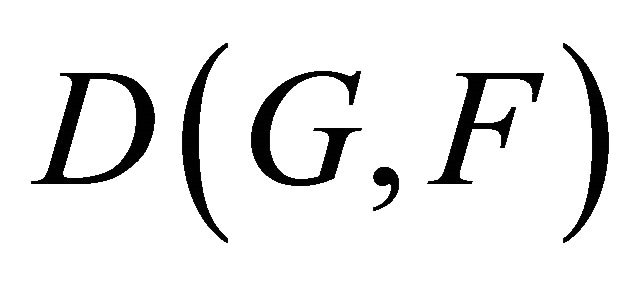 , between F and G is defined as follows
, between F and G is defined as follows
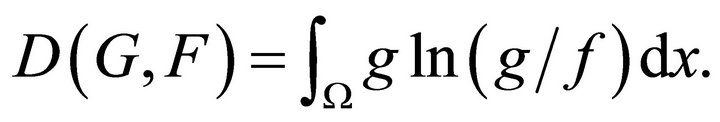 (1)
(1)
The cross-entropy 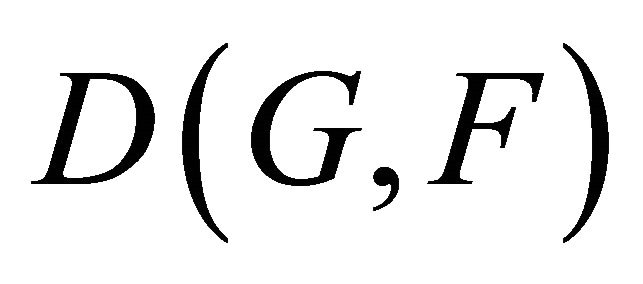 measures the differences between the unknown distribution G and the given one F. The minimum cross-entropy principle that proposed by Kullback in 1956 (See [9]), provides a rule to estimate the probability distribution which is as close as possible to the prior distribution. The distribution obtained then is supposed to be the most appropriate one that can be estimated according to the known information. The minimum crossentropy principle can be expressed as the following programming problem:
measures the differences between the unknown distribution G and the given one F. The minimum cross-entropy principle that proposed by Kullback in 1956 (See [9]), provides a rule to estimate the probability distribution which is as close as possible to the prior distribution. The distribution obtained then is supposed to be the most appropriate one that can be estimated according to the known information. The minimum crossentropy principle can be expressed as the following programming problem:
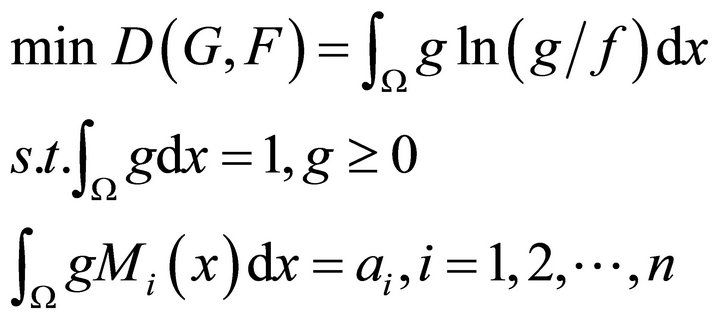 (2)
(2)
where 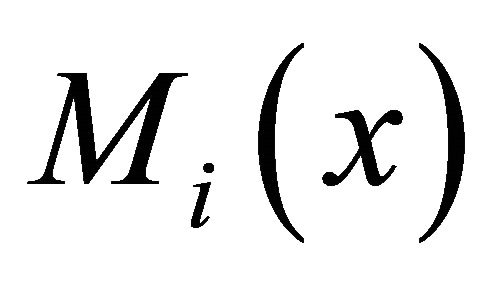 are the moment functions and ai are the observed statistical moments. The first two constraints guarantee g to be a probability density function. The moment constraints make sure the distribution g has the same statistical moments as observed.
are the moment functions and ai are the observed statistical moments. The first two constraints guarantee g to be a probability density function. The moment constraints make sure the distribution g has the same statistical moments as observed.
Proposition 2.2. The solution of problem (2) is given as follows:
 (3)
(3)
Proof. The Lagrange function of problem (2) can be written as
 where
where  are the Lagrange multipliers. The condition of optimization solution is
are the Lagrange multipliers. The condition of optimization solution is
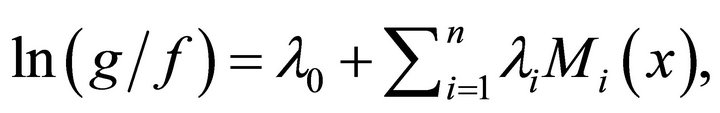 or
or
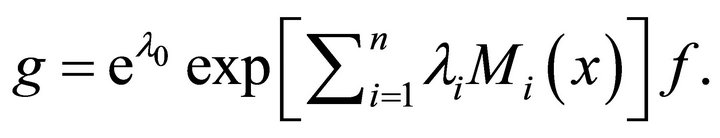 (4)
(4)
Integrating both sides of Equation (4), it infers
 (5)
(5)
Substituting Equation (5) into Equation (4), Equation (3) holds.
2.2. Modeling
Assume that the representative bank’s liabilities are all derived from deposit which is insured by the insurance company. Denote 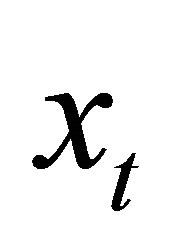 as the value of the bank’s assets at time t, and assume
as the value of the bank’s assets at time t, and assume 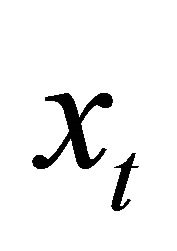 follows a lognormal process
follows a lognormal process
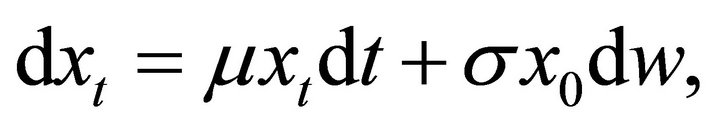
where w is a Brownian motion process, μ is the instantaneous expected rate of return of the bank’s assets, and σ is the volatility of the rate of return. Denote the deposit insurance underwriting date as 0 and define x0 as the bank’s assets value before paying the total deposit insurance premium P at the beginning of the insurance period. The bank goes bankrupt if the bank’s assets value is less than its liabilities value on the insurance expiry date T. The bank’s assets value on date T satisfies
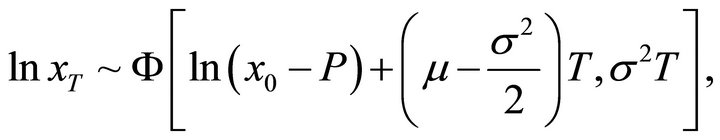
from which the probability density function of xT can be derived as follows:
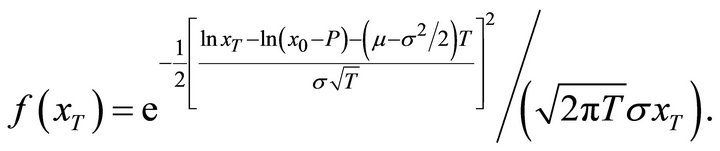 (6)
(6)
The distribution of the bank’s assets value can be obtained by integrating Equation (6), that is
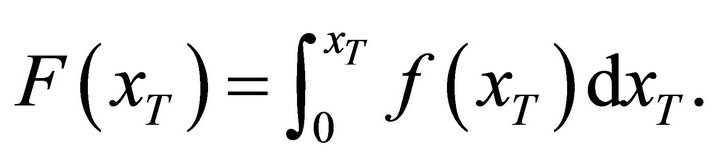 (7)
(7)
Deposit insurance may induce more benefits to the bank by strengthening the depositors’ confidence. However, after taking deposit insurance, the bank is more likely to issue riskier loans, which may increase the bank’s default risk. Under both the benefit effect and the risk effect of deposit insurance, the bank’s assets value may no longer subject to the prior lognormal distribution . Let
. Let 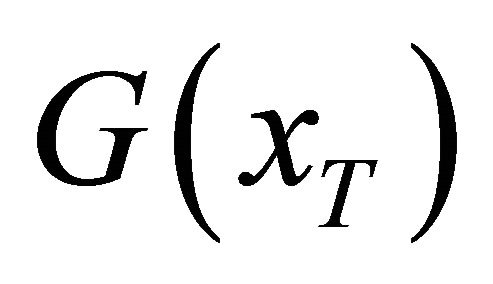 represent the distribution of the bank’s assets value considering the dual effects of deposit insurance, and
represent the distribution of the bank’s assets value considering the dual effects of deposit insurance, and 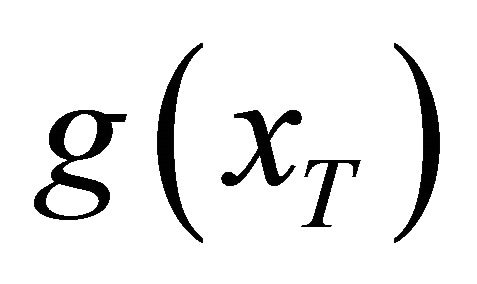 is the density function accordingly.
is the density function accordingly. 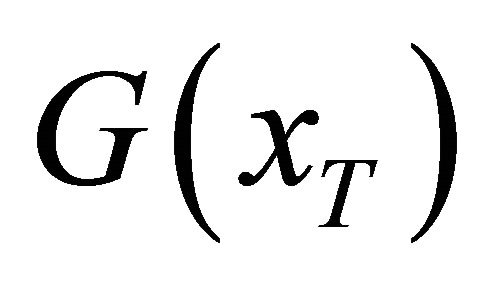 is a proximate distribution to
is a proximate distribution to . And
. And 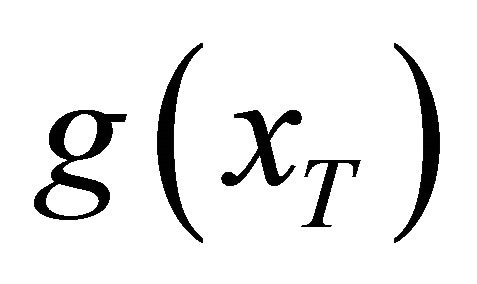 can be obtained by minimizing the crossentropy between
can be obtained by minimizing the crossentropy between 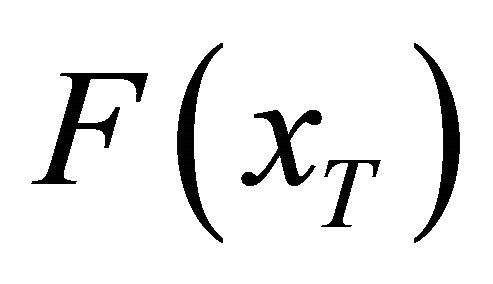 and
and 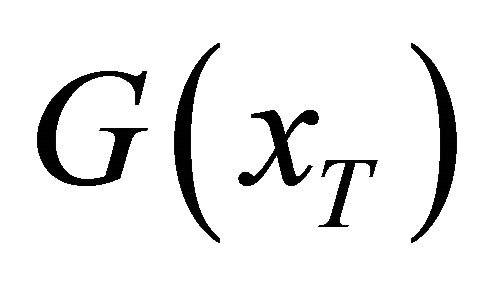 subject to some constraints, that is
subject to some constraints, that is
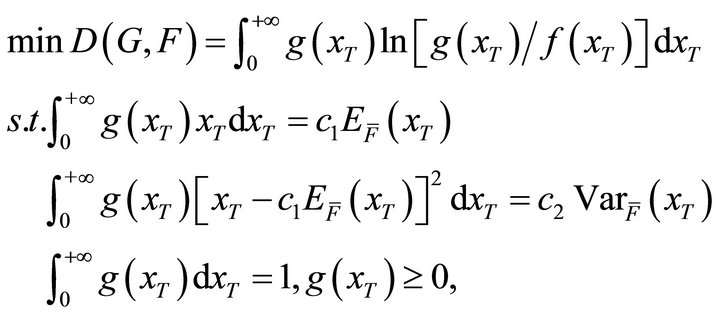 (8)
(8)
where 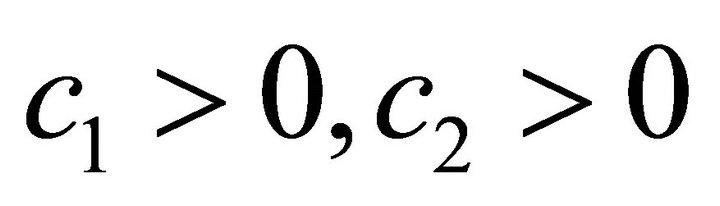 are constants, and
are constants, and
 (9)
(9)
Here  is the probability density function of the bank’s assets value before purchasing deposit insurance. It is the insurance premium P that makes
is the probability density function of the bank’s assets value before purchasing deposit insurance. It is the insurance premium P that makes  differ from
differ from . The first constraint of problem (8) measures the benefit effect of deposit insurance, while the second constraint reflects the risk effect accordingly. The dual effects of deposit insurance are determined by various factors, which can be generally divided into the bank level and the regulation level. Banks pay more attention to the benefits they may get after taking deposit insurance, which means only when
. The first constraint of problem (8) measures the benefit effect of deposit insurance, while the second constraint reflects the risk effect accordingly. The dual effects of deposit insurance are determined by various factors, which can be generally divided into the bank level and the regulation level. Banks pay more attention to the benefits they may get after taking deposit insurance, which means only when 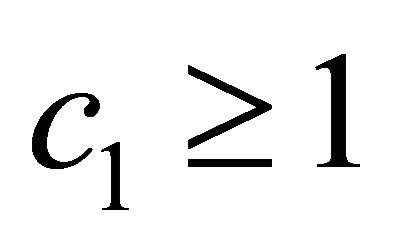 would they join the deposit insurance system, and the regulators on the other hand are also concerned with the bank’s risk taking behaviors besides the benefit efficiency. With strict supervision, which means
would they join the deposit insurance system, and the regulators on the other hand are also concerned with the bank’s risk taking behaviors besides the benefit efficiency. With strict supervision, which means , the bank is restricted to limit its assets variance no more than that without deposit insurance. However, it may not be possible to increase the bank’s benefits while decrease the relevant risk. Sometimes the supervisors have to tolerate some extra risk so as to attain the benefit objects. Using a small positive constant, ε, as the maximal extent of tolerance, the forbearance supervision is described by
, the bank is restricted to limit its assets variance no more than that without deposit insurance. However, it may not be possible to increase the bank’s benefits while decrease the relevant risk. Sometimes the supervisors have to tolerate some extra risk so as to attain the benefit objects. Using a small positive constant, ε, as the maximal extent of tolerance, the forbearance supervision is described by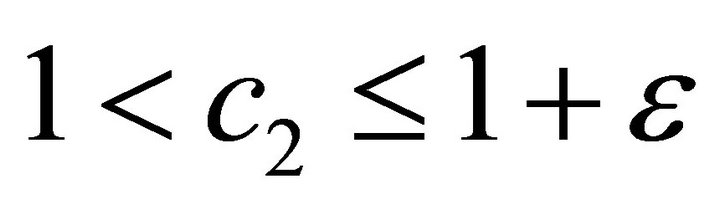 . Also, in the extreme case where there is no supervision at all, the second constraint of problem (8) would be omitted.
. Also, in the extreme case where there is no supervision at all, the second constraint of problem (8) would be omitted.
According to proposition 2.2, the solution of problem (8) can be written as
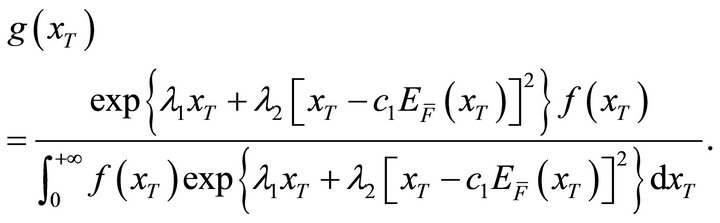 (10)
(10)
2.3. Scenarios
Three scenarios are described to discuss the corresponding probability distributions of the bank’s assets value under different benefit and regulatory constraints.
• Scenario I: Strong benefit motivation with no supervision.
The corresponding minimum cross-entropy problem can be written as
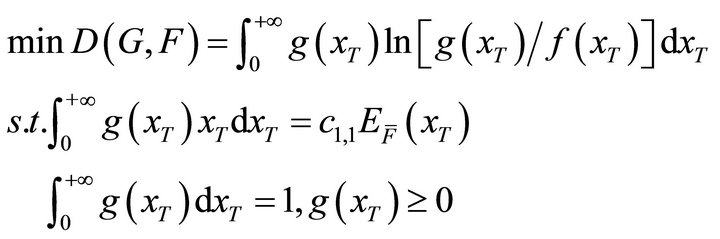 (11)
(11)
where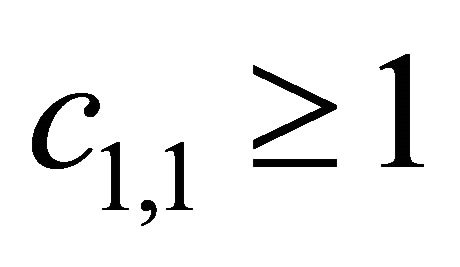 . According to Equation (10), the density function
. According to Equation (10), the density function 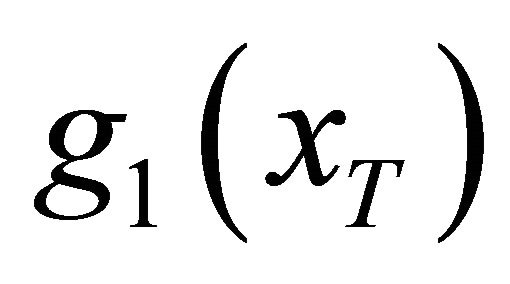 is
is
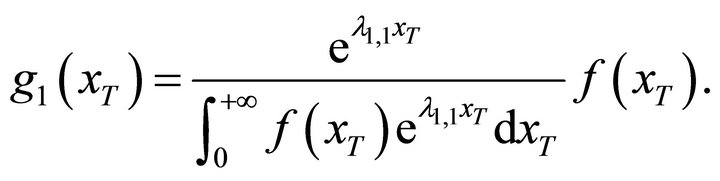 (12)
(12)
• Scenario II: Strong benefit motivation with tolerant supervision.
The minimum cross-entropy problem is listed as
 (13)
(13)
where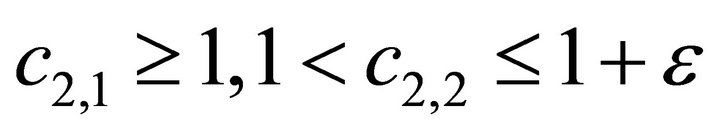 . Also, the density function
. Also, the density function  is
is
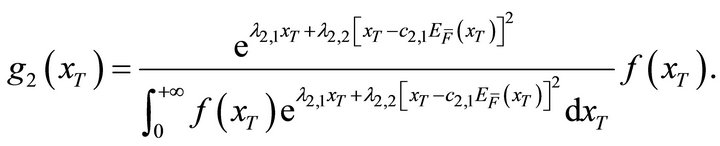 (14)
(14)
• Scenario III: Neutral benefit motivation with strict supervision.
The following minimum cross-entropy problem represents this situation.
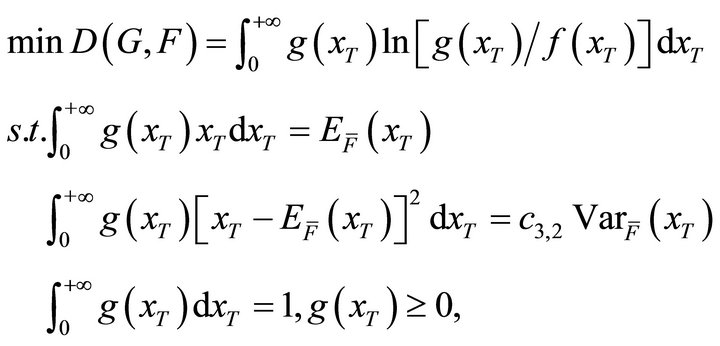 (15)
(15)
where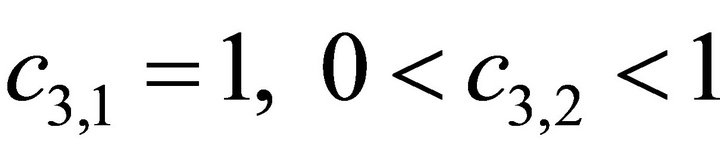 . The density function
. The density function 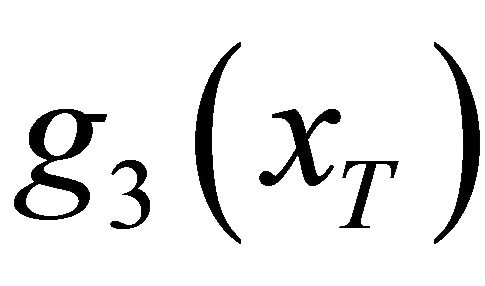 is
is
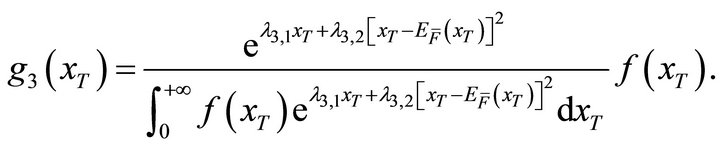 (16)
(16)
2.4. Calculation Method
It should be noticed that Equations (12), (14) and (16) are not the final solutions of 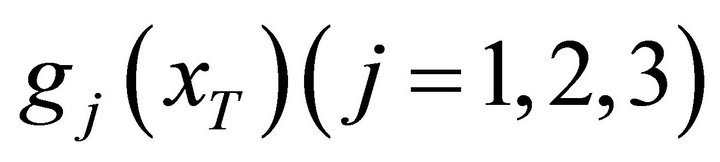 for the Lagrange multipliers are not determined. Here dual method
for the Lagrange multipliers are not determined. Here dual method
is used to calculate the Lagrange multipliers. Substituting Equations (12), (14) and (16) into the Lagrange functions of problem (11), (13) and (15) respectively, the dual problems of the three minimum cross-entropy programmings given in the scenarios above are as follows:
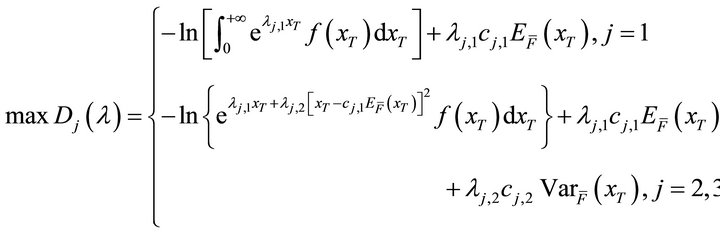 (17)
(17)
Suppose 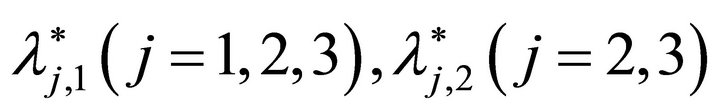 are the optimal solutions to Equation (17). Substituting
are the optimal solutions to Equation (17). Substituting 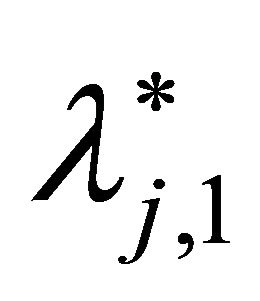 and
and  into Equations (12), (14) and (16), the density function
into Equations (12), (14) and (16), the density function  can be obtained as
can be obtained as
 (18)
(18)
It can be seen from Equation (18) that the density function 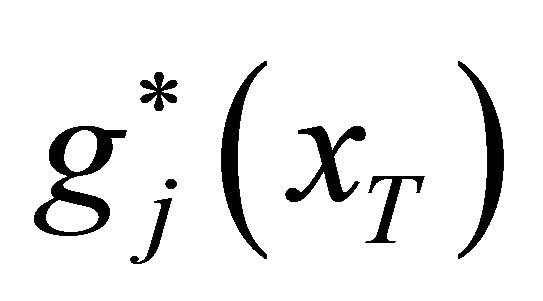 is determined by
is determined by 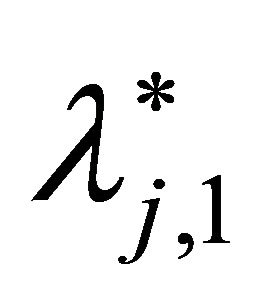 and
and  which are actually influenced by the bank’s benefit motivation along with the supervision level. Thereby, the density function
which are actually influenced by the bank’s benefit motivation along with the supervision level. Thereby, the density function  are affected by
are affected by 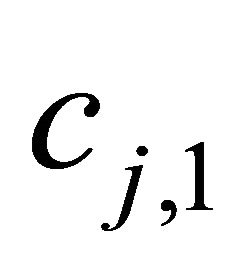 and
and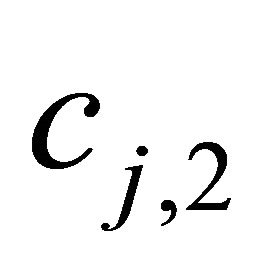 .
.
The bank’s expected assets value  and the corresponding variance
and the corresponding variance 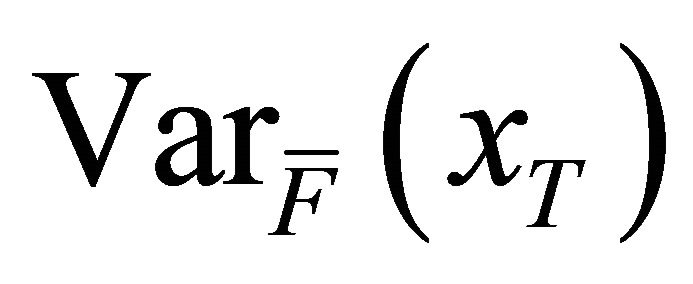 before purchasing deposit insurance should be calculated so as to clarify the constraints of the minimum cross-entropy problem. Both of the two variables can be calculated from Equation (9)1.
before purchasing deposit insurance should be calculated so as to clarify the constraints of the minimum cross-entropy problem. Both of the two variables can be calculated from Equation (9)1.
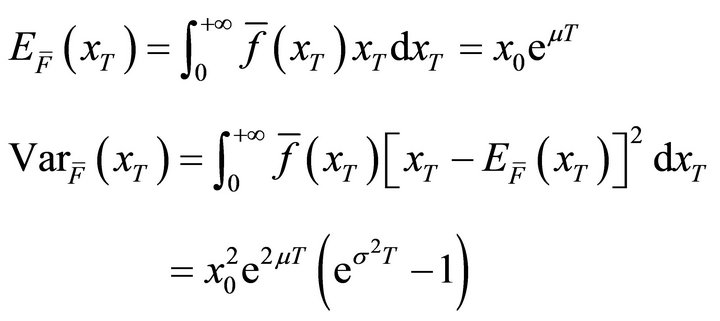 (19)
(19)
Another factor implied in 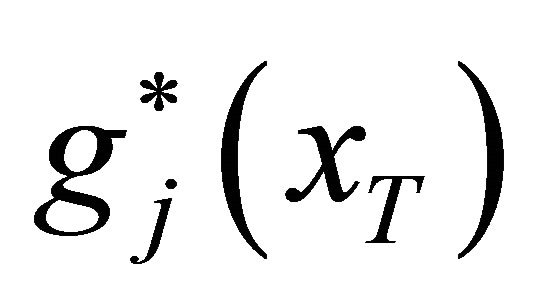 is the deposit insurance premium P. The total premium consists of the net premium and the extra premium. The net premium is equal to the actuarial present value of the insurer’s total claim payments on date T and the extra premium is used to compensate the unexpected risk the insurer may encounter. The premium P can be calculated as2
is the deposit insurance premium P. The total premium consists of the net premium and the extra premium. The net premium is equal to the actuarial present value of the insurer’s total claim payments on date T and the extra premium is used to compensate the unexpected risk the insurer may encounter. The premium P can be calculated as2
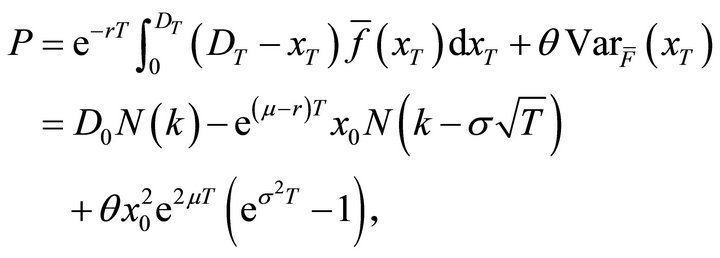 (20)
(20)
where 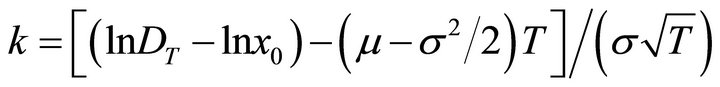 and r is the risk-free interest rate and
and r is the risk-free interest rate and 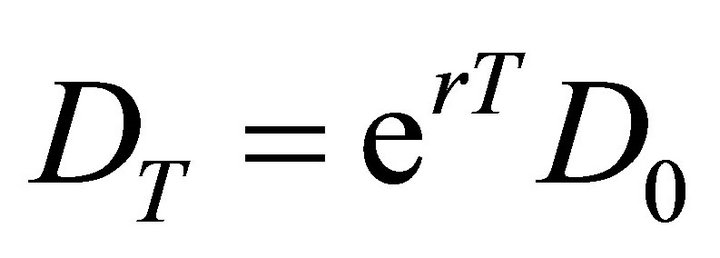 is the accumulated future value of the bank’s deposit value on date T using the risk free interest rate.
is the accumulated future value of the bank’s deposit value on date T using the risk free interest rate. 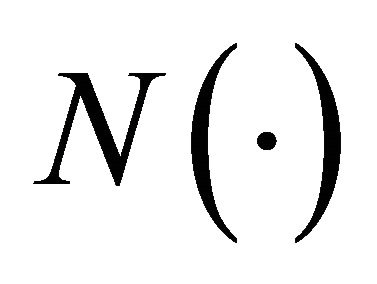 is the standard normal distribution function, and θ is defined as an additional safety factor.
is the standard normal distribution function, and θ is defined as an additional safety factor.
Substituting Equations (19), (6) and (20) into problem (17), the Lagrange multipliers  and
and  can be obtained by solving the relevant dual problems in (17)3. Putting the estimated
can be obtained by solving the relevant dual problems in (17)3. Putting the estimated  and
and  along with Equations (7) and (19) into Equation (18),
along with Equations (7) and (19) into Equation (18), 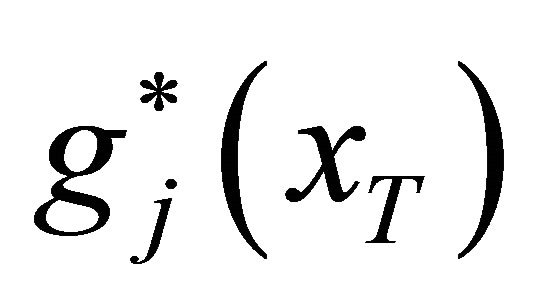 can be derived then.
can be derived then.
3. Simulation
3.1. Basic Simulation Results
Suppose the representative bank’s assets value is 7 billion RMB on date 0, of which the deposit accounts for 90 percent. The term of the deposit is one year and so is the duration of the deposit insurance. The expected rate of return on bank assets is 0.225, and the volatility of the rate of return is 0.135. To compute the insurance premium, the additional safety factor θ should be assigned. There is no extra premium when θ equals zero. The assumption of 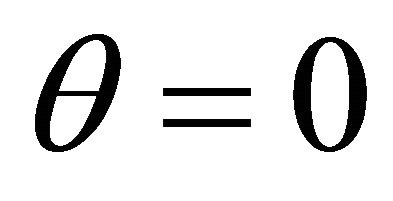 is used to calculate the basic simulation results here, and the consequence of other cases will be discussed in the next section. The risk-free interest rate is assumed to be 2.25%. The values of the parameters are given in Table 1.
is used to calculate the basic simulation results here, and the consequence of other cases will be discussed in the next section. The risk-free interest rate is assumed to be 2.25%. The values of the parameters are given in Table 1.
Using the parameters given in Table 1, the expected assets value before purchasing deposit insurance and the corresponding variance can be calculated by Equation (19). The insurance premium is obtained via Equation (20). The calculating results are listed in Table 2.
For scenario I, 5% increase of the bank’s expected assets value is assumed. Both the expectation and the variance of the bank’s assets value are supposed to increase by 2.5% in scenario II. Scenario III describes the situation with no change of the bank’s expected assets value and 5% decrease of assets variance. The corresponding value of cj,1 and cj,2 are listed in Table 3. Minimizing problem (17) can determine the optimal Lagrange multipliers. The results are given in Table 3.
The estimated probability density functions can be obtained using the values of  and
and 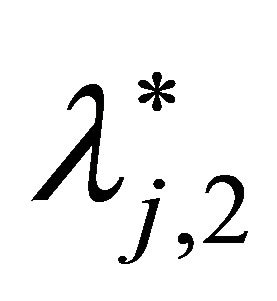 in Table 3. Figure 1 shows the curves of the density functions. Compared with the original density function
in Table 3. Figure 1 shows the curves of the density functions. Compared with the original density function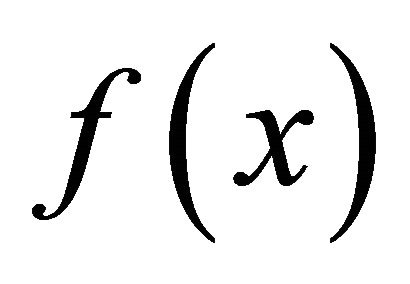 , the adjusted density functions reveal different features. The density functions
, the adjusted density functions reveal different features. The density functions 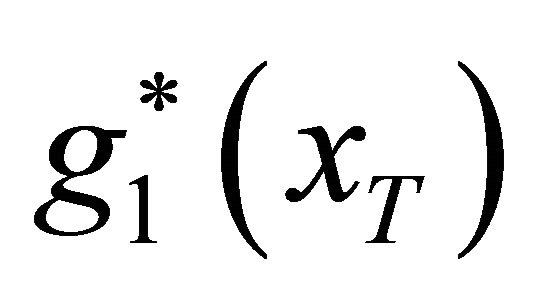 and
and 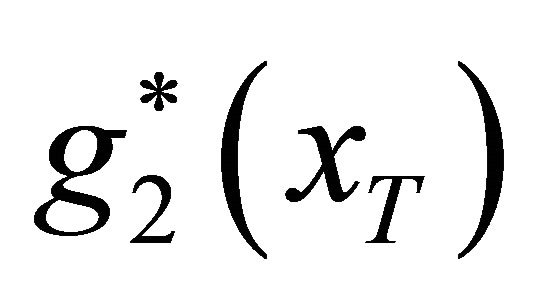 stand for the situations of no supervision and tolerant supervision respectively with the same benefit effects of deposit insurance. As can be seem from Figure 1, the distribution
stand for the situations of no supervision and tolerant supervision respectively with the same benefit effects of deposit insurance. As can be seem from Figure 1, the distribution 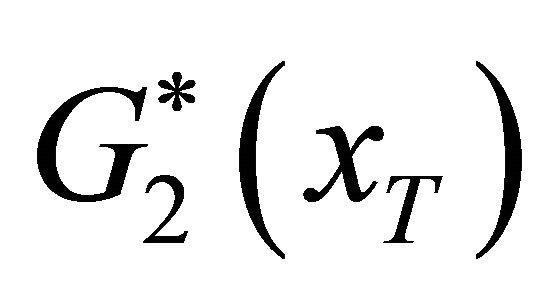 is more concentrated than the distribution
is more concentrated than the distribution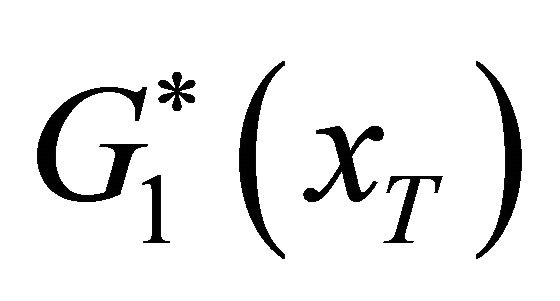 , which means the supervision level positively affects the risk aversion effects of deposit insurance under the same benefit effects. The same pattern also can be seen from the comparison of the density
, which means the supervision level positively affects the risk aversion effects of deposit insurance under the same benefit effects. The same pattern also can be seen from the comparison of the density  and the density
and the density , which reflects the situation of the same benefit effects and two different supervision levels.
, which reflects the situation of the same benefit effects and two different supervision levels.
The density function  shows a positive change of the expected assets value compared with
shows a positive change of the expected assets value compared with 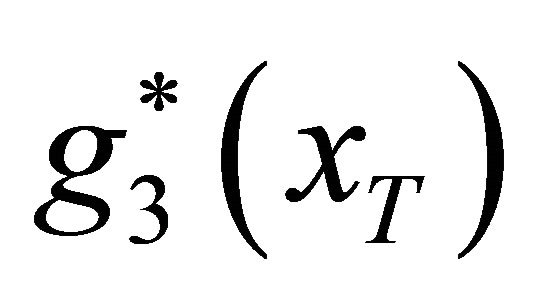 and
and
Table 1. The value of the parameters.

Table 2. The calculated results of the intermediate variables.
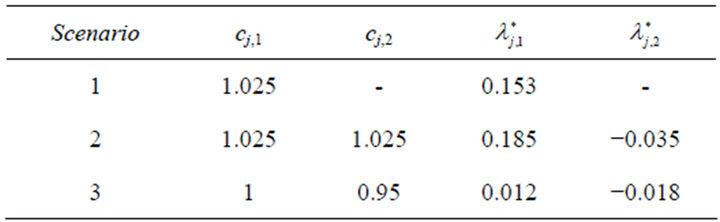
Table 3. The Lagrange multipliers.
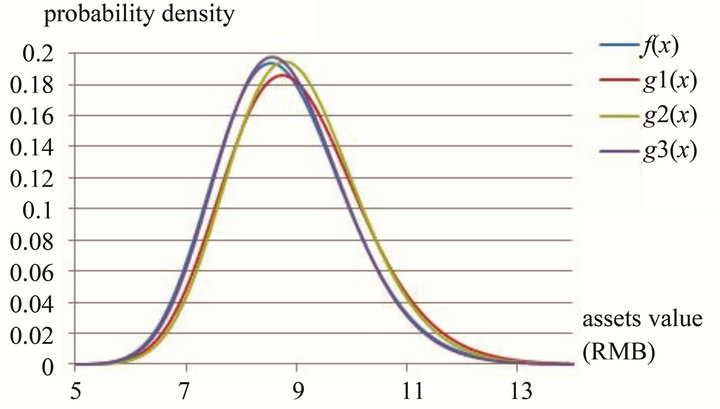
Figure 1. The estimated probability densities.
a negative difference with the assets variance of . To consider the benefit effect and the risk effect of deposit insurance at the same time, the distribution
. To consider the benefit effect and the risk effect of deposit insurance at the same time, the distribution 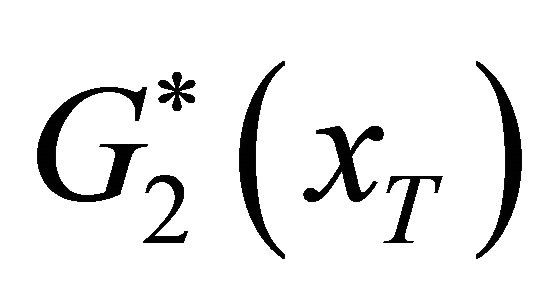 may be an ideal one for it represents the case of an increase of benefit and an acceptable level of risk.
may be an ideal one for it represents the case of an increase of benefit and an acceptable level of risk.
3.2. Effects of Safety Premium
In this section, the additional safety factor θ is set to be 0.001 and 0.01 so as to measure the effects of the safety premium. The values of 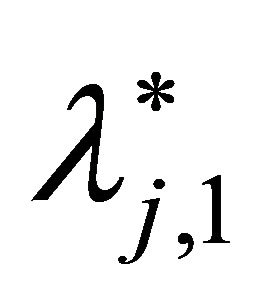 and
and 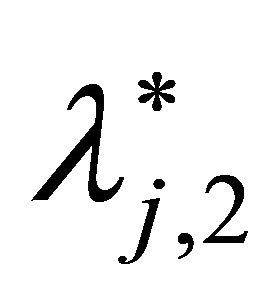 with different θ are given in Table 4. The shapes of the density functions accordingly are given in Figure 2. Compared with the bank’s total assets, the premium of deposit insurance is relatively minor. For that reason, the effects of the additional premium to the assets density function are also limited. The blue curve in Figure 2 represents the density function
with different θ are given in Table 4. The shapes of the density functions accordingly are given in Figure 2. Compared with the bank’s total assets, the premium of deposit insurance is relatively minor. For that reason, the effects of the additional premium to the assets density function are also limited. The blue curve in Figure 2 represents the density function 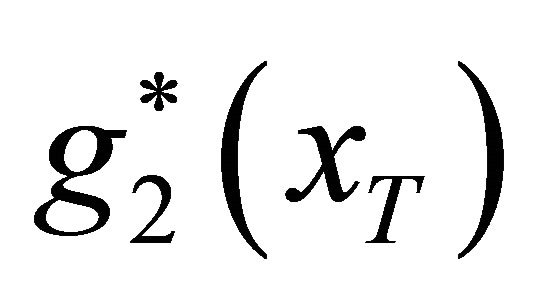 with no additional premium while the red one stands for the same function but with additional premium. The red curve deviates from the blue one slightly to the right side.
with no additional premium while the red one stands for the same function but with additional premium. The red curve deviates from the blue one slightly to the right side.
4. Conclusions
Considering both the benefit effects and the risk effects of deposit insurance, this paper provides a method to estimate the probability distribution of the bank’s assets value based on the minimum cross-entropy principle.
Three scenarios are given to describe situations with different dual effects of deposit insurance. The corresponding assets distribution functions are obtained respectively. The results show that the supervision level positively affects the risk aversion effects of deposit insurance under the same benefit effects. While the increase of the deposit insurance premium moves the bank’s assets distribution slightly to the right side. The distributions, which are estimated under different benefit and risk objects, can be taken as a reference for banks to choose the proper credit projects.
The scenarios constructed in this paper are simple and limited. Taking into account some more complicated conditions, the model can be improved. Moreover, this paper
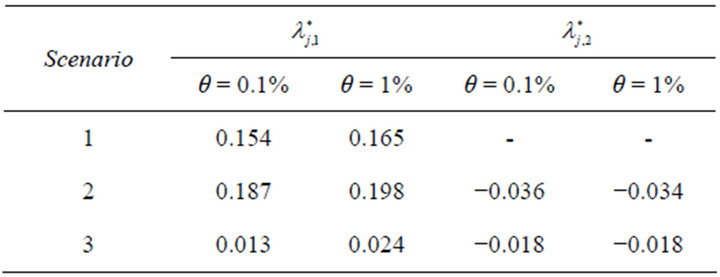
Table 4. Lagrange multipliers.
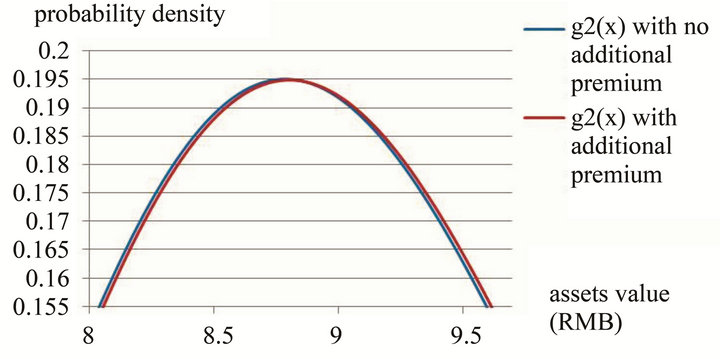
Figure 2. The top part of the density 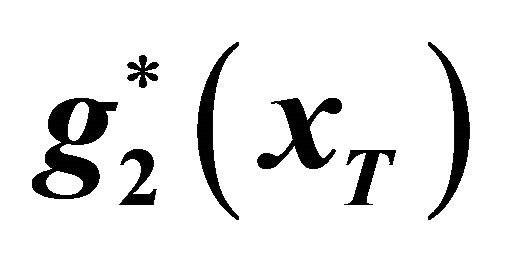 with and without additional premium4.
with and without additional premium4.
aims only at estimating the assets distributions affected by deposit insurance. Other analysis such as the distortion level that may be measured by calculating the crossentropy between the original and estimated assets distributions will be discussed in further research.
5. Acknowledgements
The research is supported by National Science Foundation of China (71171032), and the central university special funds for basic research business expenses (DUT11- RW202).
REFERENCES
- J. C. Du, A. F. Moreau and C. W. Sealey, “Fixed-Rate Deposit Insurance and Risk-Shifting Behavior at Commercial Banks,” Journal of Banking & Finance, Vol. 16, No. 4, 1992, pp. 715-742. doi:10.1016/0378-4266(92)90004-J
- A. Hovakimian and E. Kane, “Effectiveness of Capital Regulation at U.S. Commercial Banks, 1985 to 1994,” Journal of Finance, Vol. 55, No. 1, 2000, pp. 451-468. doi:10.1111/0022-1082.00212
- N. Prean and H. Stix, “The Effect of Raising Deposit Insurance Coverage in Times of Financial Crisis—Evidence from Croatian Microdata,” Economic Systems, Vol. 35, No. 4, 2011, pp. 496-511. doi:10.1016/j.ecosys.2011.01.004
- R. Iyer and M. Puri, “Understanding Bank Runs: The Importance of Depositor-Bank Relationships and Networks,” Working Paper, The National Bureau of Economic Research (NBER), Cambridge, 2008.
- L. Mbarek and D. M. Hmaied, “Deposit Insurance and Bank Risk-shifting Incentives: Evidence from the Tunisian Banking System,” Journal of Money, Investment & Banking, Vol. 20, 2011, pp. 41-53.
- V. P. Ioannidou and M. F. Penas, “Deposit Insurance and Bank Risk-Taking: Evidence from Internal Loan Ratings,” Journal of Financial Intermediation, Vol. 19, No. 1, 2010, pp. 95-115. doi:10.1016/j.jfi.2009.01.002
- L. Chernykh and R. A. Cole, “Does Deposit Insurance Improve Financial Intermediation? Evidence from the Russian Experiment,” Journal of Banking & Finance, Vol. 35, No. 2, 2011, pp. 388-402. doi:10.1016/j.jbankfin.2010.08.014
- M. Monoyios, “The Minimal Entropy Measure and an Esscher Transform in an Incomplete Market Model,” Statistics and Probability Letters, Vol. 77, No. 11, 2007, pp. 1070-1076. doi:10.1016/j.spl.2007.01.008
- M. Avellanada, “Minimum Relative-Entropy Calibration of Asset-Pricing Models,” International Journal of Theoretical and Applied Finance, Vol. 1, No. 4, 1998, pp. 447-472. doi:10.1142/S0219024998000242
NOTES

1From Equation (9): 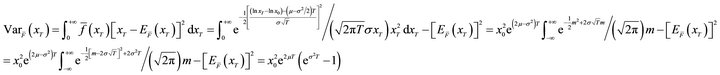
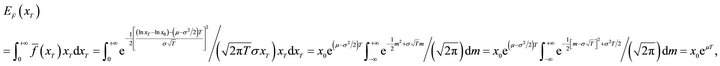
where .
.
2The insurer’s total claim payments on date T can be described as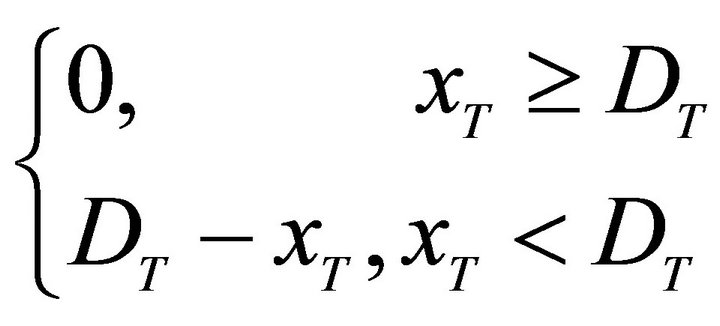 . Thus the net premium can be calculated as
. Thus the net premium can be calculated as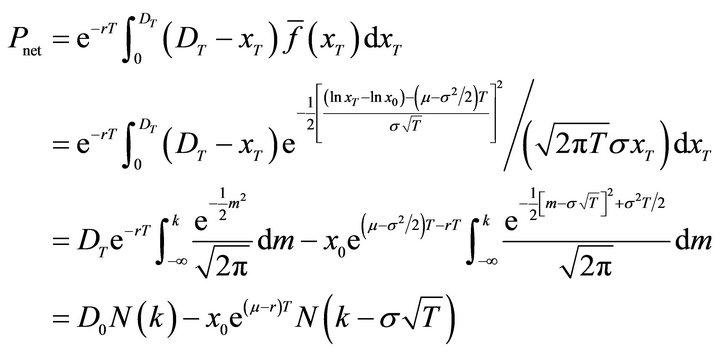 , where
, where . Substituting equation (19) into Equation (20), the total premium P equals
. Substituting equation (19) into Equation (20), the total premium P equals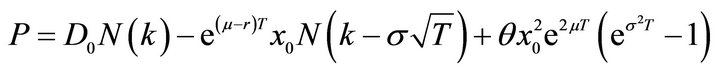 .
.
3Here Matlab 7.0 is used to write a program to solve problem (17).
4The differences between the two density functions can not be seen clearly if the whole figure, instead of the top parts, is given here for the reason discussed in the paper.

