Theoretical Economics Letters
Vol. 3 No. 1 (2013) , Article ID: 28150 , 10 pages DOI:10.4236/tel.2013.31005
A Note on Timing of Endogenous Wage Bargaining: The Case of Complements*
1Graduate School of International Studies, Pusan National University, Pusan, South Korea
2Division of Global Finance and Banking, Inha University, Incheon, South Korea
Email: choipnu@pusan.ac.kr, #skymh@inha.ac.kr
Received November 22, 2012; revised December 23, 2012; accepted January 25, 2013
Keywords: Bargaining; Complements; Cournot-Bertrand Competition; Social Welfare
ABSTRACT
By introducing Cournot and Bertrand competition in adifferentiated goods with the case of complements into Nash bargaining solution problem, we investigate timing of endogenous wage setting where wages can be negotiated either simultaneously or sequentially. Contrary to the case of substitutes, we show that regardless of the bargaining power, the type of product market competition (Cournot or Bertrand) and the degree of complementarity, 1) bargaining over wages is always simultaneous when the goods are complements; and 2) the social welfare under both Cournot and Bertrand competitions can improve when bargaining over wages is simultaneous.
1. Introduction
In the literature on unionized oligopolies, there has been analyzed regarding the bargaining process between the firm and the union. For instance, in a spatial context, Brekke and Straume [1] haveanalyzed how equilibrium locations in location-price games under Hotelling’s model are affected when wage negotiations occur simultaneously. Specifically, Barcena-Ruiz and Casado-Izaga [2] extend the findings of Brekke and Straume [1] by analyzing a duopoly in which firms choose their location and bargain over wages with their unions when the goods are substitutes. Thus, they showed that both unions prefer sequential wage-setting and that the timing of wage setting does not alter the location equilibrium. Moreover, Barcena-Ruiz and Casado-Izaga [2] demonstrate that bargaining over wages is simultaneous if and only if both firms decide when negotiation takes place; otherwise, negotiation takes place sequentially.
However, none of these papers have considered the case in which firms choose to bargain over wages of the endogenous timing when goods are complements. Specifically, Horn and Wolinsky [3] showed that when there is a single input upstream firm, the total profit of downstream industry is smaller or greater under monopoly than under duopoly according to whether the goods are substitutes or complements1. However, Horn and Wolinsky [3] restricted their attention to the case of substitutes of sequential wage negotiating and they do not analyze how firms and unions choose to bargain over wages of the endogenous timing when goods are complements. Therefore, by introducing differentiated goods with complements under either Cournot or Bertrand competition, we attempt to examine the situation where both firms or unions or one firm and one union can either simultaneously or sequentially bargain over wages. Thus, we extend Horn and Wolinsky [3], and Barcena-Ruiz and Casado-Izaga [2] by considering the timing of endogenous wage-setting and both Cournot and Bertrand competitions in a duopoly context where outputs and prices are chosen simultaneously.
Consequently, we demonstrate that regardless of the bargaining power, the type of product market competition (Cournot or Bertrand) and the degree of complementarity, bargaining over wages in unionized duopoly is always simultaneous when the goods are complements. This is because when the goods are complements, each union has a strictly dominant strategy for simultaneous wage-setting, under which the firms pay lower wages and produce more outputs and obtain more profits is obtained in the unionized duopolistic market. Hence, when the goods are complements to each other, it does not matter whether the timing of wage setting is established by: only the two unions; only the two firms; the two unions and only one firm or one union and both firms. Second, we find that regardless of the bargaining power, the type of product market competition (Cournot or Bertrand) and the degree of complementarity, the social welfare under both Cournot and Bertrand competitions can improve when bargaining over wages in a unionized duopoly is simultaneous. These results, when the choice of timing of endogenous wage setting is set in a unionized duopoly, differ from the standard findings of De Fraja [5], Corneo [6], and Barcena-Ruiz and Casado-Izaga [2]. They show that if the goods are substitutes, unions prefer to play sequentially when wage bargaining is decentralized at the level of the firm.
2. Relationship to the Literature
In this section, we discuss the relationship between our paper and some other previous theoretical papers on the bargaining process between the firm and the union.
For non-spatial contexts, theoretical studies that introduce the timing of endogenous wage-setting (i.e., the setting of input costs) into Cournot type of oligopolistic markets include De Fraja [5] and Corneo [6], among others when the goods are substitutes. De Fraja [5] and Corneo [6] show that in aoligopoly, when wage bargaining is decentralized at the level of the firm, unions prefer to play sequentially and vice versa. On the other hand, there have been some attempts, namely, Davidson [7], Naylor [8], Dorwrick [9], Horn and Wolinsky [3,10] and Lommerud et al. [11], to introduce the downstream firm negotiating with its labor union into a model of Nash bargaining. Further, as De Fraja [5] and Corneo [6] suggested, Horn and Wolinsky [3] showed that a single supplier prefers to set the input price with one firm and only then with the other firm in where a single supplier faces two firms that produce substitutes.
In a companion paper, the formal structure of the model is closely related to Choi [12]. Choi [12] considers the case in which both private and public firms choose to set over wages of the endogenous timing in a unionized mixed duopoly without generalized Nash bargaining between union-firm pair regarding both utility of union and firm’s profit (i.e., wage-setting is modelled as that of a monopoly union). Furthermore, introducing only Cournot-type of product market competition into the endogenous timing of wage-setting, Choi [12] investigates social welfare and privatization depending on the nature of goods and the timing of wage-setting in either a unionized-mixed or a unionized-privatized duopolistic market. Thus, Choi [12] demonstrates that regardless of the type of unionized duopoly competition (mixed or privatized duopoly) and the degree of complementaritywage-setting is always simultaneous if the goods are complements under only Cournot competition. Otherwise, the standard results occur when the goods are substitutes, as De Fraja [5], Corneo [6], and Barcena-Ruiz and Casado-Izaga [2] point out2. Instead, by introducing the generalized Nash bargaining power into unionized duopoly, we investigate how firms and unions choose to bargain over wages of the endogenous timing when goods are complements under either Cournot or Bertrand competition. Therefore, present paper is complement to Choi [12], which guarantees the robustness of our result when bargaining between the utility of union and firm’s profit takes places.
3. The Model
Consider a unionized duopoly situation for a differentiated good that is supplied by two firms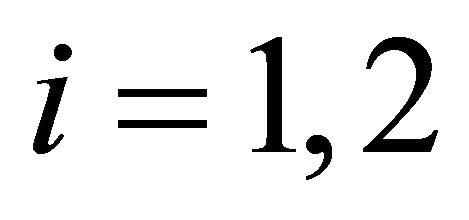 . On the demand side of the market, the representative consumer’s utility is a quadratic function given by
. On the demand side of the market, the representative consumer’s utility is a quadratic function given by
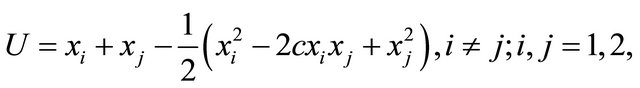
where 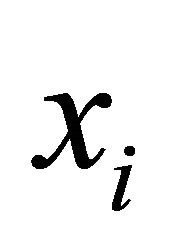 denotes the output of firm
denotes the output of firm . Let
. Let 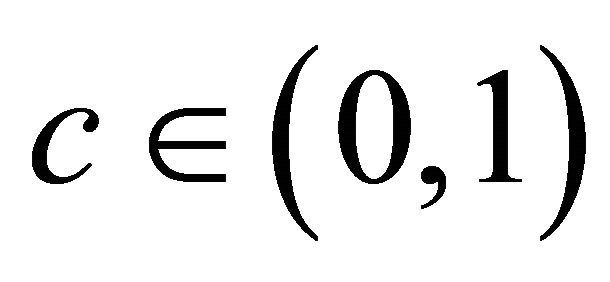 denote the extent of product differentiation with goods assumed to beim perfect complements3. Thus, when the goods are complements, the inverse demand is characterized by
denote the extent of product differentiation with goods assumed to beim perfect complements3. Thus, when the goods are complements, the inverse demand is characterized by
 (1)
(1)
where is firm i’s market price.
is firm i’s market price.
To analyze the union’s wage bargaining, we also assume that both firms are unionized and that the wages,  , are determined as a consequence of bargaining between firms and their respective unions. The utility of unions is wage bill:
, are determined as a consequence of bargaining between firms and their respective unions. The utility of unions is wage bill: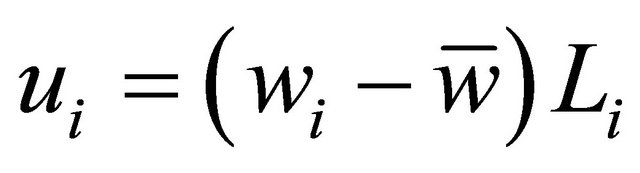 . For ease of exposition, let
. For ease of exposition, let 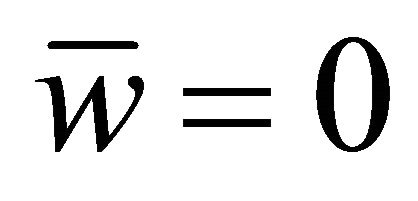 and Li denote the reservation wage and the number of workers who are employed by firm i, respectively. On the other hand, the firms are homogeneous with respect to productivity. Each firm adopts a constant returns-to-scale technology where one unit of labor is turned into one unit of the final good; thus,
and Li denote the reservation wage and the number of workers who are employed by firm i, respectively. On the other hand, the firms are homogeneous with respect to productivity. Each firm adopts a constant returns-to-scale technology where one unit of labor is turned into one unit of the final good; thus,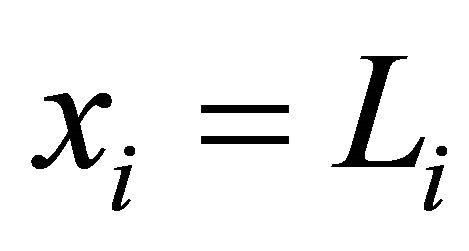 . We consider a variant of the right to manage model, where employment is set unilaterally by the firm (see also Booth [14]). Taking
. We consider a variant of the right to manage model, where employment is set unilaterally by the firm (see also Booth [14]). Taking  as a given, we assume that the wages are determined through Nash bargaining. The solution is wages
as a given, we assume that the wages are determined through Nash bargaining. The solution is wages 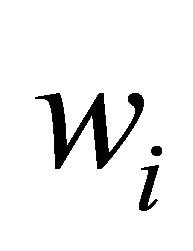 such that
such that 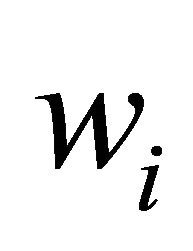 is the Nash solution to the bargaining problem between union i and the firm i, given that both expect to agree upon the price
is the Nash solution to the bargaining problem between union i and the firm i, given that both expect to agree upon the price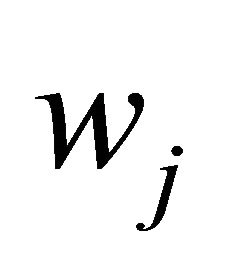 . That is, given
. That is, given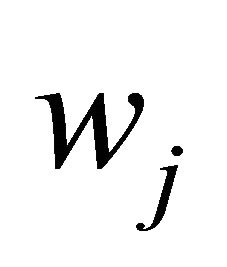 , the bargaining problem between union
, the bargaining problem between union  and the firm i is described by the payoff pairs
and the firm i is described by the payoff pairs
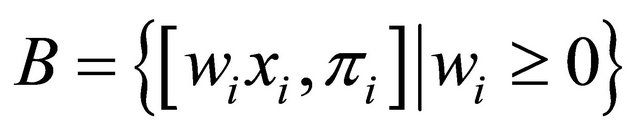 and the disagreement point (0,0)where
and the disagreement point (0,0)where  is the profit of the firm i. The solution is given by:
is the profit of the firm i. The solution is given by:
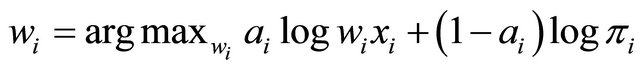 (2)
(2)
where 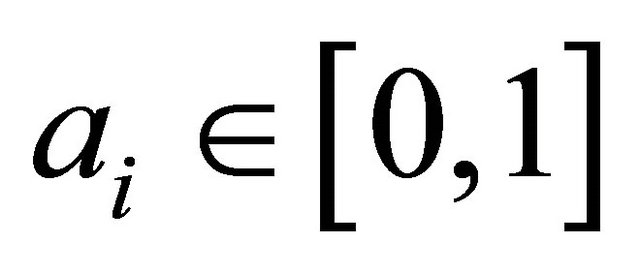 measures the bargaining power of union i relative to that of the firm i. For ease of exposition, we assume that
measures the bargaining power of union i relative to that of the firm i. For ease of exposition, we assume that  to show our results in a simple way. The papers that are closest to our representation of the unions’ utilities are Davidson [7], Naylor [8], Dorwrick [9], Horn and Wolinsky [3,10] and Lommerud et al. [11]. As they suggest, each downstream firm negotiates with its labor union, which maximize the input wage level and number of workers. This is a departure from the framework of traditional models that involves each union has the same bargaining power across the firms.
to show our results in a simple way. The papers that are closest to our representation of the unions’ utilities are Davidson [7], Naylor [8], Dorwrick [9], Horn and Wolinsky [3,10] and Lommerud et al. [11]. As they suggest, each downstream firm negotiates with its labor union, which maximize the input wage level and number of workers. This is a departure from the framework of traditional models that involves each union has the same bargaining power across the firms.
Each firm’s profit is as following function
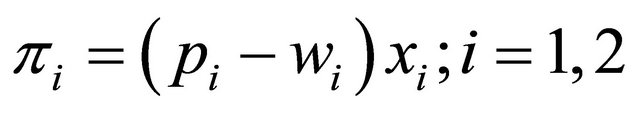 (3)
(3)
where the price of labor (i.e., wage) that firm i has to pay is denoted by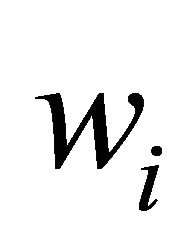 ,
, .
.
Timing of the second-stage game is as follows. In the first stage, either firms or unions simultaneously decide whether to negotiate over wages in either period 1 or period 2. Note that decision of timing of wage bargaining could be taken in each case by the firms, by the union or a firm and its union in lieu of being chosen by firms or unions to decide the production quantities (or equivalently, the workforce levels). If the periods of negotiation happen to be identical, the wage bargaining process is simultaneous, in which cases a Cournotand Bertrandtype game occur respectively; otherwise, the wage bargaining process is sequential. In the second stage, each firm simultaneously chooses its quantity or price to maximize its respective objective knowing each union’s choice of the wage level.
4. Cournot Equilibrium under Unionized Duopoly
In this paper, since we focus on symmetric Nash equilibrium, we assume that all firms choose the same type of bargaining. Thus, the game is solved by backward induction, i.e., the solution concept used is the subgame perfect Nash equilibrium.
This section examined the impact of a duopoly in terms of the extent of the timing of wage bargaining, which would be established in the case of a unionized duopoly. We discuss one Cournotand two Stackelbergtype unionized-duopoly models of fixed timing.
4.1. Simultaneous Bargaining over Wages under Cournot Competition
In the second stage, taking as  and solving the firstorder conditions (3), we obtain,
and solving the firstorder conditions (3), we obtain,
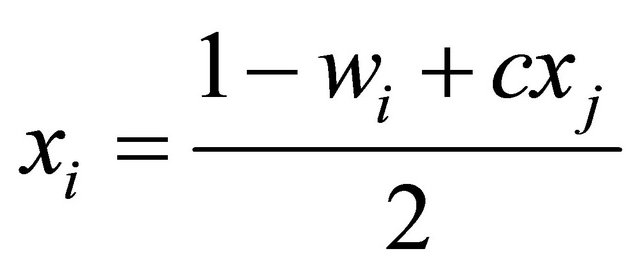 (4)
(4)
Straightforward computation yields each equilibrium output as follows:
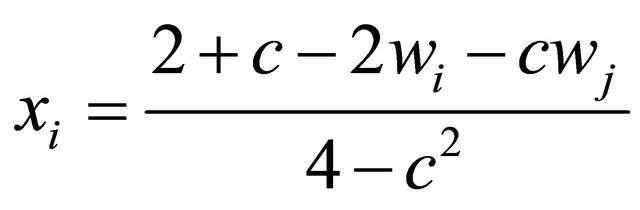 (5)
(5)
From (5), the each firm’s profit,  , in the unionized duopoly can be rewritten as follows:
, in the unionized duopoly can be rewritten as follows:
 (6)
(6)
We now move to the first stage of the game. Using (5), the problem for union i is defined as
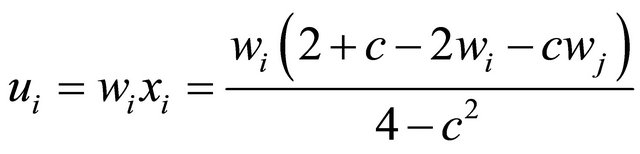
The wage wi is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
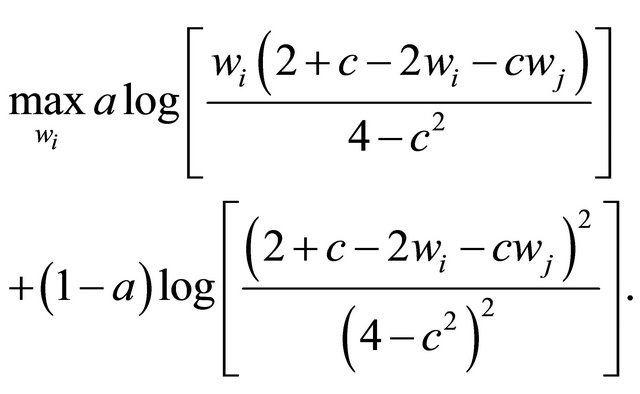
This implies the following first-order condition
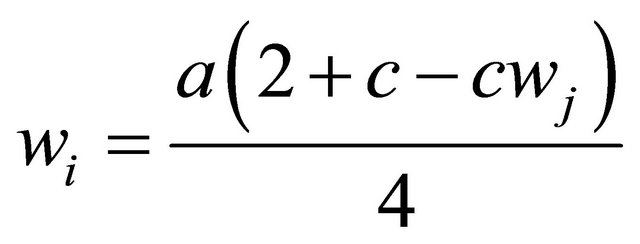 (7)
(7)
The symmetry across unions yields that (in following the superscript “c” stands for the case of simultaneous bargaining over wages under Cournot competition)
 (8)
(8)
Substituting each wage equilibrium value into (5) yields each equilibrium output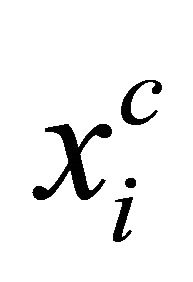 , firm’s profit and utility of union yields that
, firm’s profit and utility of union yields that
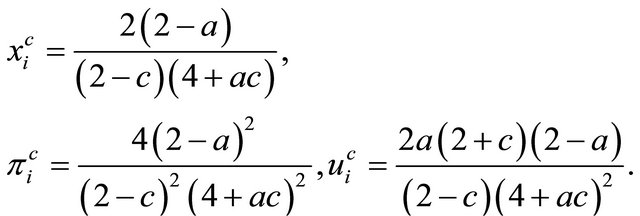 (9)
(9)
4.2. Sequential Bargaining over Wages under Cournot Competition
In this case, we discuss that the firm i or its union acts as the leader regarding wage setting. To solve for the backwards-induction wage setting of this game, we use the firm j’s union reaction function 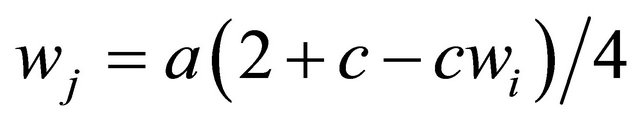 as in the case of simultaneous bargaining over wages under Cournot competition4. To distinguish notations, let the superscript “l” stand for the leader and “f” for the follower. Thus, we obtain each output level as follows;
as in the case of simultaneous bargaining over wages under Cournot competition4. To distinguish notations, let the superscript “l” stand for the leader and “f” for the follower. Thus, we obtain each output level as follows;
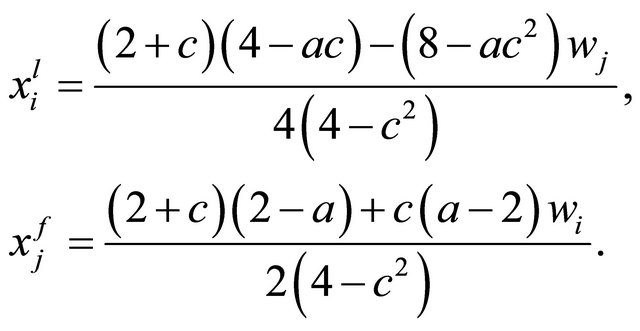 (10)
(10)
Hence, the utility of union i is obtained as follows:
 (11)
(11)
Straightforward computation yields each firm’s profit;
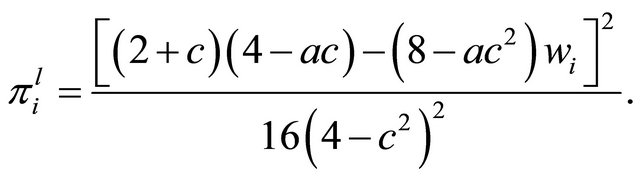 (12)
(12)
As mentioned earlier, the wage 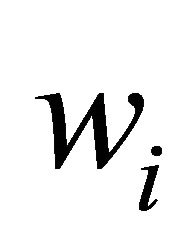 is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have

Straightforward computation yields each equilibrium wage as follows:
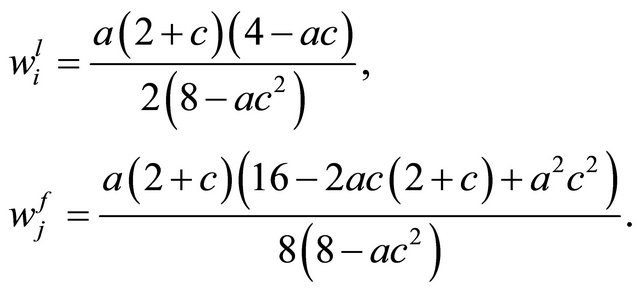 (13)
(13)
Therefore, substituting (13) into (10), (11) and (12) yields each equilibrium output, utility of union and firm’s profit yields that
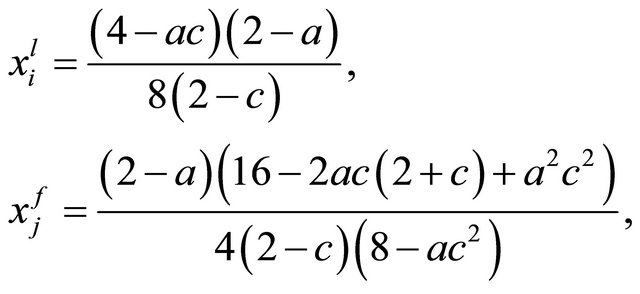 (14)
(14)
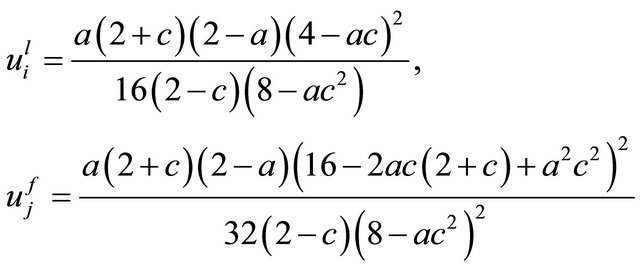 (15)
(15)
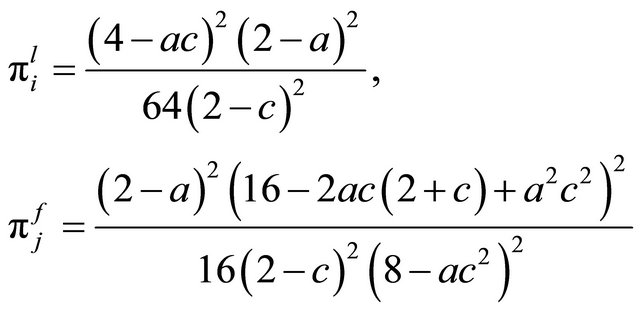 (16)
(16)
5. Bertrand Equilibrium under Unionized Duopoly
In this section, we assume that the product market game in the stage 2 is characterized by Bertrand competition by firms. Thus, we examined the impact of a duopoly in terms of the extent of the timing of wage bargaining, which would be established in the case of a unionized duopoly.
We discuss one Bertrandand two Stackelberg-type unionized-duopoly models of fixed timing. From (1) and its rival firm j, we can rewrite product demand function facing firm i as
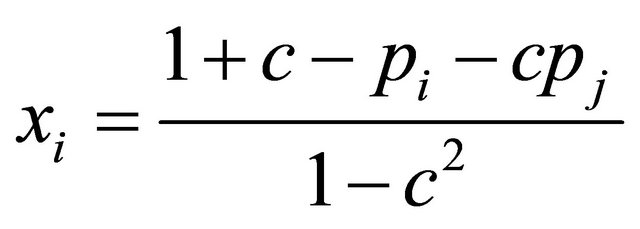 . (17)
. (17)
Thus, profits of firm i are given by
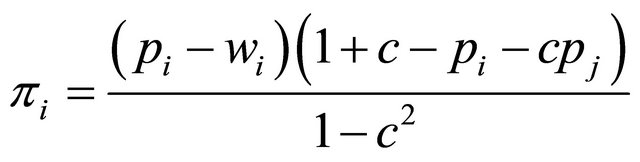 (18)
(18)
when goods are complements.
5.1. Simultaneous Bargaining over Wages under Bertrand Competition
In the second stage, taking as wi and solving the firstorder conditions (18), we obtain,
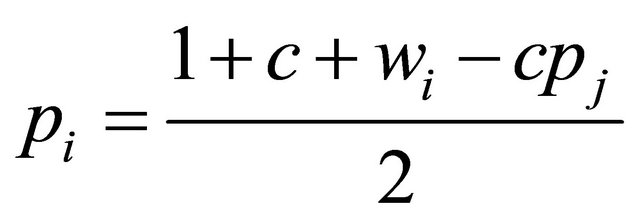 . (19)
. (19)
Straightforward computation yields each equilibrium price and output as follows:
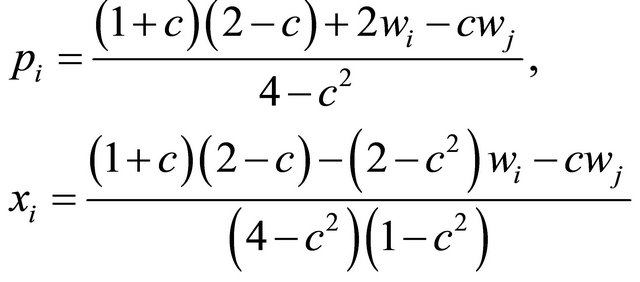 (20)
(20)
From (20), the each firm’s profit,  , in the unionized duopoly can be rewritten as follows:
, in the unionized duopoly can be rewritten as follows:
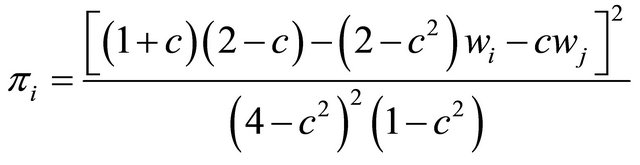 . (21)
. (21)
We now move to the first stage of the game. Using (20), the problem for union i is defined as

The wage  is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
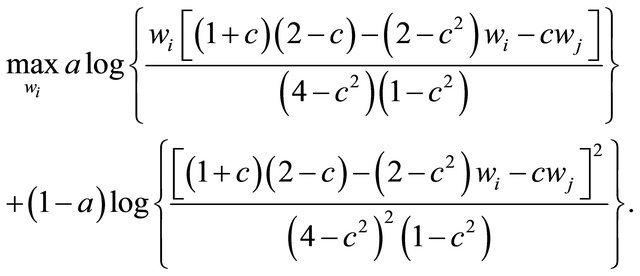
This implies the following first-order condition
 . (22)
. (22)
The symmetry across unions yields that (in following the superscript “B” stands for the case of simultaneous bargaining over wages under Bertrand competition)
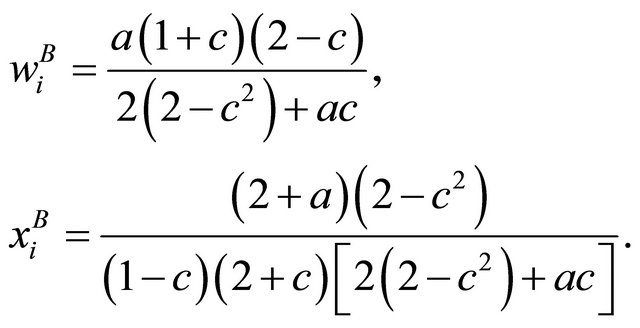 (23)
(23)
Substituting each wage equilibrium values into (20) yields each equilibrium output  , firm’s profit and utility of union as follows;
, firm’s profit and utility of union as follows;
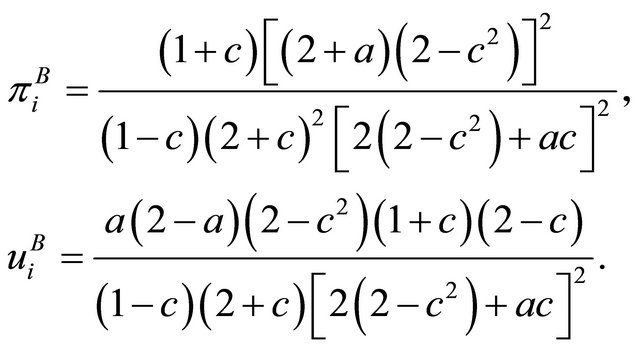 (24)
(24)
5.2. Sequential Bargaining over Wages under Bertrand Competition
In this case, we discuss that the firm i or its union acts as the leader regarding wage setting. To solve for the backwards-induction wage setting of this game, we use the firm j’s union reaction function

as in the case of simultaneous bargaining over wages under Bertrand competition. To distinguish notations, let the superscript “L” (respectively, “F”) denote the equilibrium value in the case of leadership (respectively, followership) wage bargaining that the rival firm takes as given. Thus, we obtain each output level as follows:
 (25)
(25)
Hence, the utility of union i is obtained as follows:
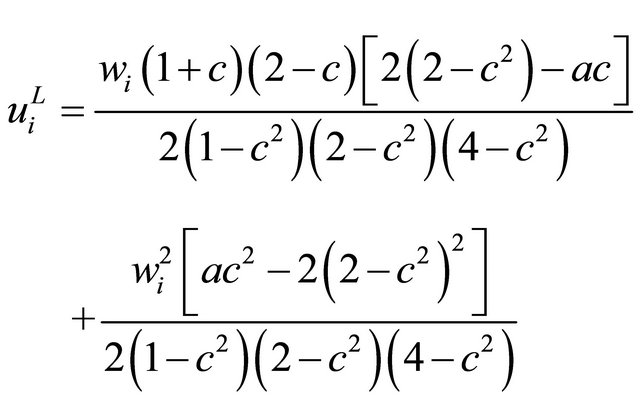 (26)
(26)
Straightforward computation yields each firm’s profit;
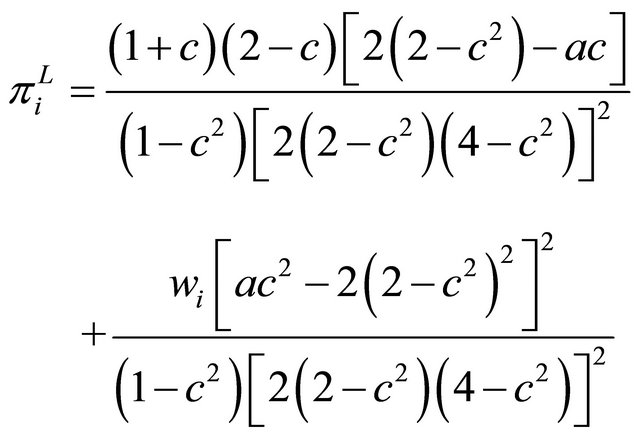 (27)
(27)
As mentioned earlier, the wage  is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
is determined through Nash bargaining. Applying the maximization problem in (2) to this situation, we have
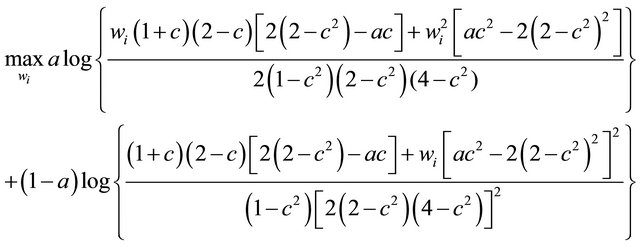
Straightforward computation yields each equilibrium wage as follows:
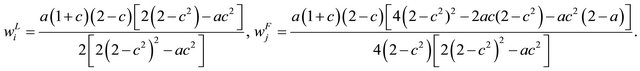 (28)
(28)
Therefore, substituting (28) into (25), (26) and (27) yields each equilibrium outputs, utilities of unions and firms’ profits as follows:
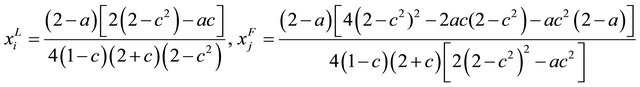
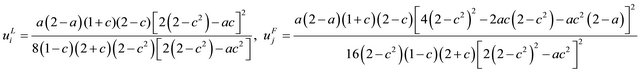
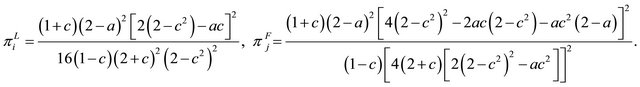
6. Choice of Bargaining Timing and Social Welfare
Having derived the equilibrium for three fixed-timing games in the previous section and using the same notation for the timings as before, we can determine firm’s endogenous timing that each takes the utilities of unions and firms’ profits and social welfare as a given.
Let “F” and “S” represent first period and second period with regard to timing choice of wage setting respectively. When agents (the firms or the unions) have chosen “F” or “S”, they will play a Cournotor Bertrand-type game of the wage setting in the first stage; when one firm’s agent has chosen “F” while the other’s agent has chosen “S”, Stackelberg-type game of the wage setting arises in the second stage and vice versa.
In this section, we will find the Nash equilibrium in the first stage for any given utilities of the unions and the profits of firms under duopoly. The reduced endogenous-timing game among unions can be represented by the following payoff table.
To find the subgame-perfect Nash equilibrium, we need to compare utilities of unions. From Table 1, straitforward computations show that
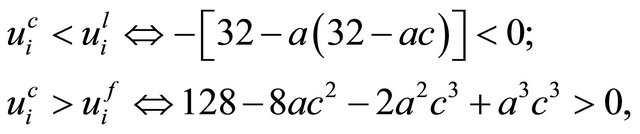

These inequalities tell us that regardless of whether the type of product market is Cournot or Bertrand competition, each firm’s union prefers simultaneous wage setting to sequential wage setting. So there is a unique subgame perfect Nash equilibrium of wage-setting: (F, F). Thus, we have the following lemma:
Lemma 1. Suppose that the goods are complements and that the decision of the timing of wage setting is delegated to unions in duopoly market. Then, there can be sustained a unique endogenous order of wage setting. The order is (F, F).
The intuition in the case of complements is as follows. The fact that the first opportunity of wage setting in duopoly market is the strictly dominant strategy for all unions plays an important role in the derivation of the re
Table 1. Timing of wage setting between Union i and Union j.

Note that * = c, α = l, β = f if Cournot competition and * = B, α = L, β = F if Bertrand competition.
sult.
It is clearly always better to be a leader than a follower. Contrary to the case of substitutes of wage setting, we show that unions choose to wages in the first opportunity when goods are complements: Although the number of workers employed in the simultaneous case is more than the number employed when the union is a follower (i.e., 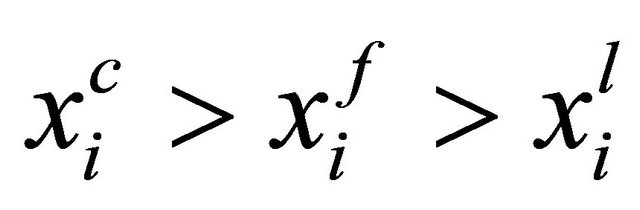 and
and ), each union gets higher wages in the leader union (i.e.,
), each union gets higher wages in the leader union (i.e., and
and ). This implies that both unions obtain greater utilities under the simultaneous case than under the sequential case. Therefore, regardless of both the bargaining power, the type of product market competition (Cournot or Bertrand) and the degree of complementarity, all unions prefer to set the wages simultaneously in duopoly market5.
). This implies that both unions obtain greater utilities under the simultaneous case than under the sequential case. Therefore, regardless of both the bargaining power, the type of product market competition (Cournot or Bertrand) and the degree of complementarity, all unions prefer to set the wages simultaneously in duopoly market5.
Similar to the timing of wage setting among unions, the reduced endogenous-timing game among firms can be represented by the following payoff tables.
To find the subgame-perfect Nash equilibrium, we need to compare each firm’s profit. Straightforward computations show in Table 2 that
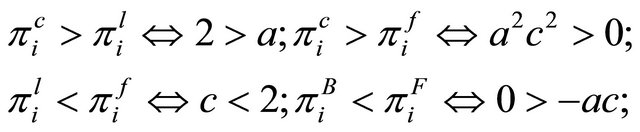
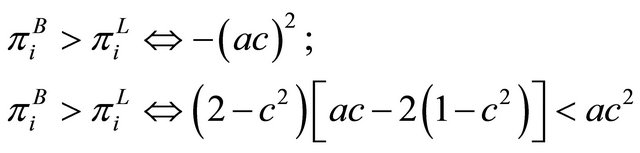
These inequalities tell us that each firm prefers simultaneous wage setting to sequential wage setting. So there are multiple subgame perfect Nash equilibria in the timing of endogenous wage-setting: (F, F), (S, S). Thus, we have the following lemma:
Lemma 2. Suppose that the decision of the timing of wage setting is not delegated to the unions in duopoly market. Then, when the goods are complements, duopoly market can always sustain multiple subgame-perfect
Table 2. Timing of wage setting between Firm i and Firm j.

Note that * = c, α = l, β = f if Cournot competition and * = B, α = L, β = F if Bertrand competition.
equilibria; the order is either (S, S) or (F, F).
The intuition of Lemma 2 is as follows. Lemma 2 confirms that regardless of the bargaining power, the type of product market competition and the degree of complementarity, the simultaneous negotiation of wages yields greater profits. In Lemma 1, we have considered that when the goods are complements, the workers employed in the simultaneous case are more than those in the sequential case and the unions get lower wages in the simultaneous case6. From the viewpoint of the firms, in the simultaneous case, they pay lower wages, produce more outputs, and realize more profits, which leads to the results  and
and . As a result, the firms in the simultaneous case get greater profits than that in the sequential case. Thus, both firms prefer to simultaneously set wages.
. As a result, the firms in the simultaneous case get greater profits than that in the sequential case. Thus, both firms prefer to simultaneously set wages.
Given Lemma 1 and 2, we obtain the following result.
Proposition 1. When the goods are complements, bargaining over wages is always simultaneous, regardless of bargaining power, the degree of complementarity and the type of product market competition (Cournot or Bertrand).
Proof. Regardless of whether the type of product market is Bertrand or Cournot competition, the proof is the same from the result of Lemmas 1 and 2. Hence, we do not distinguish the type of product market competition.
First, consider the case when both unions decide the timing of wage setting. Then, both unions do not have incentives to play sequentially since there is a dominant strategy for each union, which is to bargain at the first opportunity.
Second, consider that both firms decide the timing of wage setting. As shown in Propositions 1 and 2, both firms prefer to play simultaneously regardless of c and a, i.e., they wish to bargain at either the first or the second opportunity. This case shows that both firms prefer to play simultaneously even though there is no dominant strategy.
Third, consider that the firm i and the firm j’s union decide on the timing of endogenous wage-setting. There is a dominant strategy for the firm j’s union, which is to bargain at the first opportunity. Given this, the firm igets a higher profit in the simultaneous case. Then, we have a simultaneous game at the bargaining stage.
Finally, suppose that the game is played by both firms and unions. In this case, neither union deviates from the first opportunity because both unions have a dominant strategy, which is to play at the first opportunity and be a leader. On the other hand, if one firm prefers to delay wage bargaining, then both unions have a dominant strategy, which is to play at the first opportunity and be a leader. Further, the firm does not have an incentive to deviate from the simultaneous case because its firm always prefers to play simultaneously. The same result can be obtained if the game is played by one firm and its union and vice versa. Q.E.D.
When the goods are complements, Proposition 1 is in contrast to one of the findings when the goods are substitutes, namely, that only two firms have incentives to play simultaneously (i.e., to bargain at only the second opportunity) regarding endogenous wage-setting, which can be sustained as an equilibrium outcome. In our setting, since there is a strictly dominant strategy for each union and there is no strictly dominant strategy for each firm in duopoly market when the goods are complements, all the firms and unions prefer to play simultaneously at first opportunity7. It does not matter whether the timing of wage setting is established only by the two unions, by the unions and only one firm, or by one union and both firms. That is, bargaining over wages is always simultaneous when the goods are complements.
Noting that the social welfare
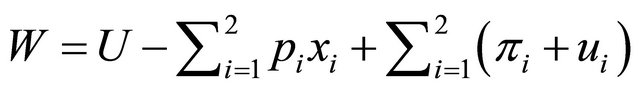
which consists of consumer surplus
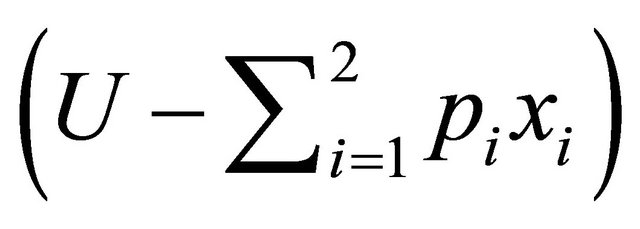 and producer surplus
and producer surplus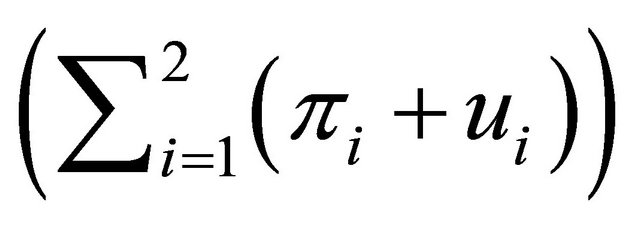 we can compute the social welfare W under either Cournot or Bertrand competition8. As shown in Propositions 1, the social welfare when the goods are complements is always determined by simultaneous timing of wage bargaining in a duopoly. Therefore, we immediately have the following proposition.
we can compute the social welfare W under either Cournot or Bertrand competition8. As shown in Propositions 1, the social welfare when the goods are complements is always determined by simultaneous timing of wage bargaining in a duopoly. Therefore, we immediately have the following proposition.
Proposition 2. Suppose that each union has same bargaining power. Then, each level of social welfare is determined by

Proof. See Appendix A. Q.E.D.
Proposition 2 suggests that regardless of the bargaining power, the type of product market competition and the degree of complementary, the social welfare is higher in the simultaneous case than in the sequential one. Therefore, when the goods are complements, larger social welfare can be obtained regardless of whether the timing of wage setting is established only by the two unions, by the unions and only one firm, or by one union and all firms. The intuition behind Proposition 2 is as follows. In this paper, we have assumed that the social welfare depends positively upon quantities produced, which consists of the representative consumer’s utility. Since equilibrium quantities are higher under either Cournot or Bertrand competition, each firm can gain a higher profit, and total output is larger by choosing simultaneous case and equilibrium price becomes smaller by choosing sequential case, social welfare is larger in the simultaneous case than in the sequential one. Proposition 2 suggests that differences in the implementation of leadership depend on the nature of goods. That is, we find that when the goods are complements, social welfare of simultaneous bargaining over wages is obtained regardless of whether the type of product market is Bertrand or Cournot competition.
7. Concluding Remarks
This study has investigated the changes in the timing of endogenous wage setting when the goods are complements under either Cournout or Bertrand competition. By introducing the timing of endogenous wage setting into the unionized duopoly-framework when the goods are complements, this study provides new insight into the timing of endogenous wage setting. We have found that regardless of the bargaining power and the degree of complementarity, bargaining over wages is always simultaneous if the goods are complements. This result indicates differences in the implementation of endogenous wage setting according to whether the goods are substitutes or complements.
Finally, in this paper, we have used simplifying assumption that each firm’s union is allowed to engage in decentralized bargaining. Furthermore, a limitation of this study is that there is different bargaining structure among the firms, which can be considered the preferred bargaining structure. Therefore, this paper does not investigate the existence of degree of centralization of union bargaining matters for all firms to choose different bargaining regime for different firms. The extension of our model in these directions remains an agendum for future research.
REFERENCES
- K. Brekke and O. R. Straume, “Bilateral Monopolies and Location Choice,” Regional Science and Urban Economics, Vol. 34, No. 3, 2004, pp. 275-288. doi:10.1016/S0166-0462(03)00046-2
- J. C. Barcena-Ruiz and F. J. Casado-Izaga, “Timing in Endogenous Bargaining over Costs and Firm Location,” Journal of Economics, Vol. 95, No. 2, 2008, pp. 149-166. doi:10.1007/s00712-008-0026-y
- H. Horn and A. Wolinsky, “Bilateral Monopolies and Incentives for Merger,” Rand Journal of Economics, Vol. 19, No. 3, 1988, pp. 408-419. doi:10.2307/2555664
- J. C. Barcena-Ruiz and M. B. Garzon, “The Organisation of Wage Bargaining in Divisionalised Firms,” Australian Economic Papers, Vol. 41, No. 3, 2002, pp. 305-319. doi:10.1111/1467-8454.00166
- G. De Fraja, “Staggered vs Synchronized Wage Setting in Oligopoly,” European Economic Review, Vol. 37, 1993, pp. 1507-1522. doi:10.1016/0014-2921(93)90119-U
- G. Corneo, “National Wage Bargaining in an International Integrated Product Markets,” European Journal of Political Economy, Vol. 11, No. 3, 1995, pp. 503-520. doi:10.1016/0176-2680(95)00006-J
- C. Davidson, “Multiunit Bargaining in Oligopolistic Industries,” Journal of Labor Economics, Vol. 6, No. 3, 1988, pp. 397-422. doi:10.1086/298189
- R, A. Naylor, “Industry Profits and Competition under Bilateral Oligopoly,” Economics Letters, Vol. 77, No. 2, 2002, pp. 169-175. doi:10.1016/S0165-1765(02)00107-6
- S. Dorwrick, “Union-Oligopoly Bargaining,” Economic Journal, Vol. 99, No. 398, 1989, pp. 1123-1142. doi:10.2307/2234092
- H. Horn and A. Wolinsky, “Worker Substitutability and Patterns of Unionization,” Economic Journal, Vol. 98, 1988, pp. 484-497. doi:10.2307/2233379
- K. E. Lommerud, F. Meland and L. Sorgard, “Unionised Oligopoly, Trade Liberalisation and Location Choice,” Economic Journal, Vol. 113, No. 490, 2003, pp. 782-800. doi:10.1111/1468-0297.t01-1-00154
- K. Choi, “Timing of Endogenous Wage Setting and Privatization in a Differentiated Industry: A Mixed-Duopoly Approach,” Mimeo, Pusan National University, Pusan, 2009.
- J. C. Barcena-Ruiz and M. L. Campo, “R&D Investment and Sequential Wage Negotiation,” Australian Economic Papers, Vol. 48, No. 3, 2009, pp. 183-202. doi:10.1111/j.1467-8454.2009.00370.x
- A. Booth, “The Economics of the Trade Union,” Cambridge University Press, Cambridge, 1995.
- J. C. Barcena-Ruiz and M. L. Campo, “Short-Term or Long-Term Labor Contracts,” Labour Economics, Vol. 7, No. 3, 2000, pp. 249-260. doi:10.1016/S0927-5371(99)00040-8
Appendix
Proof of Proposition 2: Noting that social welfare  (respectively,
(respectively, ) of simultaneous wage bargaining under Cournot (respectively, Bertrand) competition and social welfare
) of simultaneous wage bargaining under Cournot (respectively, Bertrand) competition and social welfare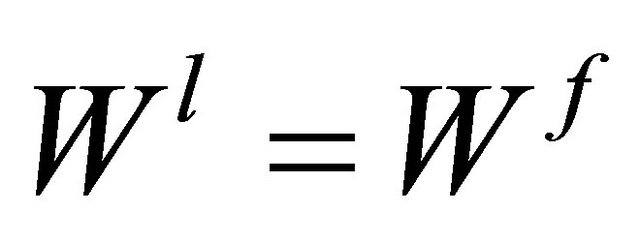 (respectively,
(respectively,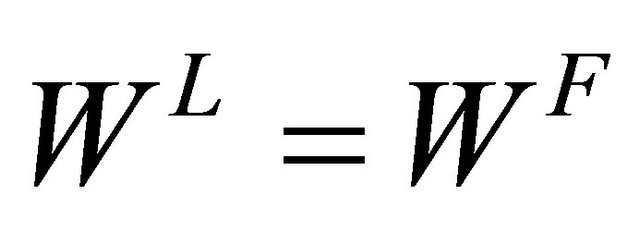 ) of sequential wage bargaining under Cournot (respectively, Bertrand) competition, we can compute the social welfare
) of sequential wage bargaining under Cournot (respectively, Bertrand) competition, we can compute the social welfare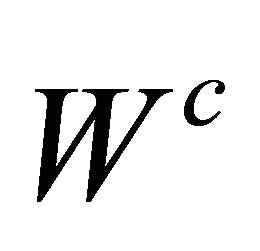 ,
, 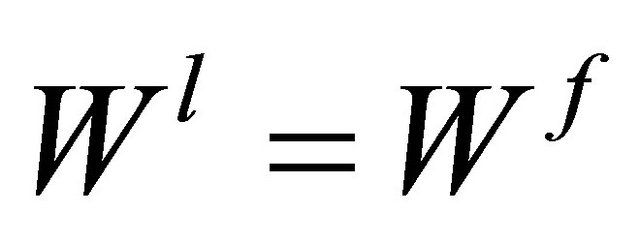 as follows;
as follows;
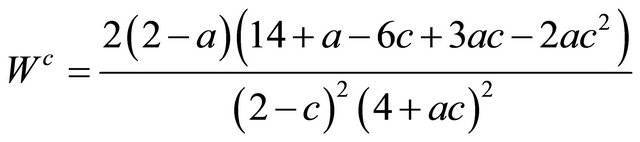 ,
,

Comparing social welfare under the simultaneous withthat under sequential wage setting, straightforward computations show under Cournot competition that9
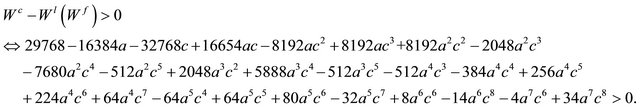
On the other hand, since comparing 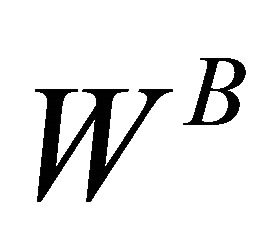 with
with 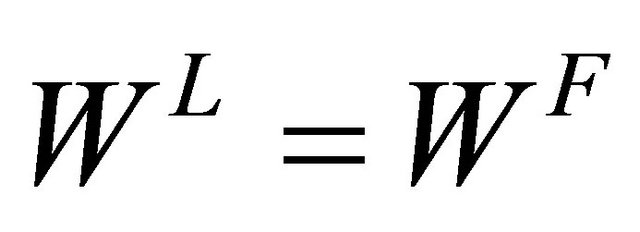 becomes complicated, so we need to use numerical examples to illustrate the impact of the degree of complementartity. Using this computation, the numerical analysis of Table A-1 shows that the social welfare of
becomes complicated, so we need to use numerical examples to illustrate the impact of the degree of complementartity. Using this computation, the numerical analysis of Table A-1 shows that the social welfare of 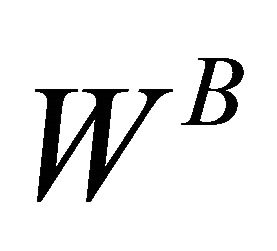 is larger than that of
is larger than that of 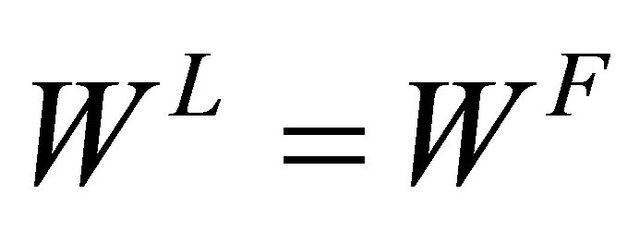 under Bertrand competition.
under Bertrand competition.
Table A-1. Numerical examples under Bertrand competition.

The positive number in each cell depicts that given the degree of complementarity, c or the bargaining power of union, α, the comparisons of social welfare implies .
.
NOTES
*This work was supported by INHA University Research Grant (INHA40279-01).
#Corresponding author.
1Barcena-Ruiz and Garzon [4] analyzed a theoretical model for case of multiproduct firms in which both unions and firms can choose their bargaining structures according to whether the goods are substitutes or complements.
2Barcena-Ruiz and Campo [13] showed that unions may choose to set wages simultaneous spending most on R&D if the size of the market is small enough and the efficiency of the R&D technology is great enough.
3In the main body of analysis, we exclude the imperfect substitutability, viz., the case when  since the detailed computations of substitutes are considered by De Fraja [5] and Corneo [6] without the timing of endogenous wage setting. We will discuss the case of substitutes later in this paper.
since the detailed computations of substitutes are considered by De Fraja [5] and Corneo [6] without the timing of endogenous wage setting. We will discuss the case of substitutes later in this paper.
4The case in which wages are bargained first in frim j is symmetric. Hence, we omit it.
5In contrast to Barcena-Ruiz and Campo [15], this result is because wages are strategic “substitutes”. When the goods are substitutes, due to the fact that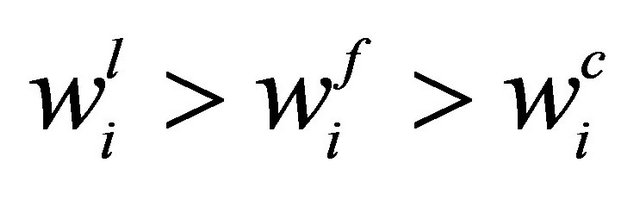 ,
, 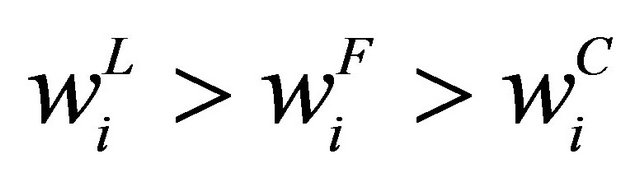 ,
,  and
and  , we obtain the results that union prefers sequential wage setting: multiple subgame-perfect Nash equilibria can be sustained as (F, S) and (S, F).
, we obtain the results that union prefers sequential wage setting: multiple subgame-perfect Nash equilibria can be sustained as (F, S) and (S, F).
6When the goods are substitutes, due to the fact that  and
and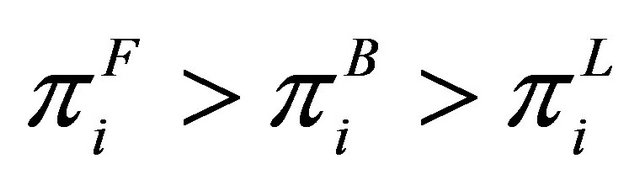 , a unique endogenous wage setting can always be sustained as (S, S).
, a unique endogenous wage setting can always be sustained as (S, S).
7When the goods are substitutes, bargaining over wages is simultaneous if and only if both firm decide on the period of time in which bargaining takes place. Otherwise, bargaining takes place sequentially.
8Utilities of unions are included as the part of producer surplus, which is usual in literature.
9Comparing 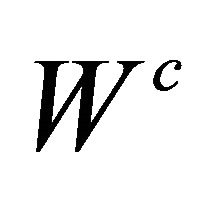 with
with 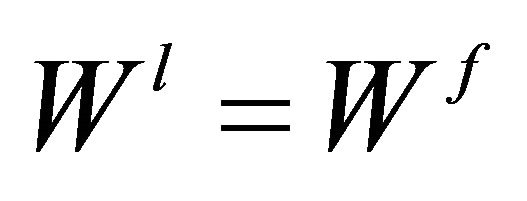 is obtained using Microsoft Office Excel.
is obtained using Microsoft Office Excel.

