Theoretical Economics Letters
Vol.2 No.3(2012), Article ID:21503,2 pages DOI:10.4236/tel.2012.23047
Another Look at Becker’s Irrational Consumer
Department of Economics, University of Illinois at Chicago, Chicago, USA
Email: rmpeck@uic.edu
Received April 1, 2012; revised May 3, 2012; accepted June 5, 2012
Keywords: Irrational Consumer; WARP; Downward Sloping Demand
ABSTRACT
Becker’s paper “Irrational Consumers and Economic Theory” ([1]) is a classic. This paper shows how to parameterize the process of selecting points randomly on a budget set. This parameterization also simplifies the proof that average demand curves are downward sloping and satisfy the weak axiom of revealed preference. In addition, we show that the probability distribution of random choices does not need to be restricted to a uniform distribution which Becker assumes. In fact, the distribution can be arbitrary.
1. Introduction
Becker’s Irrational Consumer paper ([1]) is a classic. Becker considered a consumer choosing randomly from their budget set, according to a uniform probability distribution. He then demonstrated that on average both compensated and uncompensated demand curves are downward sloping; put differently, mean choices (in a two good framework) satisfy the weak axiom of revealed preference. Becker’s demonstration was a geometric argument that made particular use of the assumption of a uniform distribution. Becker’s conclusion can be easily generalized. Here we demonstrate that if individuals randomly choose consumption bundles on their budget sets, then on average, both the compensated and uncompensated demand curves are downward sloping, irrespective of the underlying probability distribution of the random choices. The proof is surprisingly simple.
We also note that the Becker framework is formally similar to that of Hildenbrand ([2])1 but the interpretations differ. Hildenbrand characterizes average demand when there are a large number of heterogeneous infinitesimal agents while the Becker paper considers the average behavior of a single individual making a large number of repeated random choices from their budget line. One can also think of the Becker framework as a characterizing mean consumption of a large population of identical individuals each making random choices from their budget line. The Hildenbrand framework, however, is much more general; distribution of population characteristics is arbitrary and the number of goods, while finite, is not restricted to just two. Becker’s framework can easily be generalized along these lines.
2. Downward Sloping Demand in the Two Good Model
There are two goods, x and y with prices 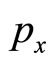 and
and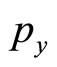 , income is I.
, income is I.  is a random variable distributed on [0, 1] with mean
is a random variable distributed on [0, 1] with mean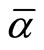 . An individual randomly chooses a point on budget line
. An individual randomly chooses a point on budget line
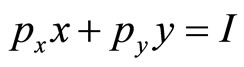
We suppose that this choice occurs as a realization of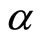 , so that
, so that
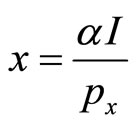
and
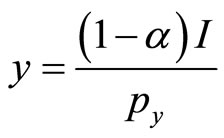 .
.
Taking expectations, average or mean demand is given by

and
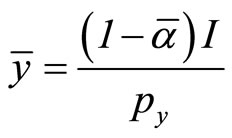
Clearly, mean demands 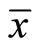 and
and 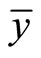 both slope downward for
both slope downward for 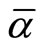 strictly between 0 and 1. Since
strictly between 0 and 1. Since , the mean demand curves
, the mean demand curves 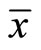 and
and 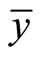 corresponds to a utility maximizing individual with Cobb-Douglas preferences. Since the mean demand curve arises from utility maximization, mean consumption conforms to WARP. It is clear, however, that there are no restrictions on the underlying distribution of
corresponds to a utility maximizing individual with Cobb-Douglas preferences. Since the mean demand curve arises from utility maximization, mean consumption conforms to WARP. It is clear, however, that there are no restrictions on the underlying distribution of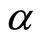 , with support [0, 1], other than the existence of a mean
, with support [0, 1], other than the existence of a mean . The case Becker considered corresponds to
. The case Becker considered corresponds to 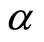 distributed uniformly on the unit interval. For this case, the mean of the distribution
distributed uniformly on the unit interval. For this case, the mean of the distribution 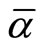 is 1/2. This argument also generalizes to more than 2 commodities, where the support of the random variable is the unit simplex, which is the set of non-negative vectors whose components add up to one.
is 1/2. This argument also generalizes to more than 2 commodities, where the support of the random variable is the unit simplex, which is the set of non-negative vectors whose components add up to one.
REFERENCES
- G. S. Becker, “Irrational Behavior and Economic Theory,” Journal of Political Economy, Vol. 70, No. 1, 1962, pp. 1-13. doi:10.1086/258584
- W. Hildenbrand, “On the Law of Demand,” Econometrica, Vol. 51, No. 4, 1983, pp. 997-1020 doi:10.2307/1912048
NOTES
1The Hildenbrand framework is much more general; distribution of population characteristics is arbitrary and the number of goods, while finite, is not restricted to just two.

