Journal of Mathematical Finance
Vol.06 No.03(2016), Article ID:70110,15 pages
10.4236/jmf.2016.63033
Pricing Loan CDS with Vasicek Interest Rate under the Contagious Model
Yinglin Liu1, Ruili Hao2*, Zuhua Wang3
1Faculty of Business and Economics, Macquarie University, Sydney, Australia
2Department of Financial Mathematics, Shanghai Finance University, Shanghai, China
3School of Mathematics, Shanghai University of Finance and Economics, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2016; accepted 23 August 2016; published 26 August 2016
ABSTRACT
This paper mainly studies the pricing of credit default swap with the loan as the reference asset under the primary-secondary model. In the contract of credit default swap (CDS), we consider that the defaults of the counterparties are correlated with the stochastic interest rate following Vasicek model or the default state of the reference firm. We assume that the company’s default is independent with the company’s prepayment and obtain the pricing formulas of the loan and loan CDS.
Keywords:
Loan CDS, Contagious Risk, Vasicek Interest Rate, Primary-Secondary Framework

1. Introduction
Since the end of the twentieth century, the derivatives market has developed rapidly and become one of the most important financial innovations in the internationally financial market. It has also become a new tool of managing credit risk after the loan transaction and the asset securitization. Credit default swap (CDS) is one of the most important derivatives to manage credit risk in the financial market.
Because it is easy to implement standardization, the credit default swap market has the rapid expansion. However, some concealed contradictions exposed gradually, such as the United States subprime crisis and the European sovereign debt crisis. They make people realize that credit derivatives bring the convenience and contain huge risk at the same time, especially contagious risk. Therefore, the pricing problem of credit default swap became a hot research topic in recent years.
Until now, there have been mainly two basic approaches to study credit risk: the structural approach and the reduced approach. The corresponding models are called the structural model and the reduced-form model. The structural approach introduced the firm’s default governed by the value of its assets and debts such as [1] [2] . However, for the problem of the valuation of credit products with jump-diffusion risk, it is still difficult to get explicit results, even using the above approaches in the event of defaulting before the maturity date. Nevertheless, the reduced-form approach is comparatively flexible and tractable to solve this problem. For the reduced-form approach, exogenous mechanism of firm’s default was introduced. This model considers the default as a random event which was controlled by an exogenous intensity process (see [3] - [5] ). With the more aggregate credit risk in the modern financial markets, we have recognized that the defaults of many firms have direct linkage. Thereby the valuation of credit securities with contagious risk has aroused a lot of authors’ interests. The model of credit contagion was firstly proposed to account for the concentration risk in large portfolios of defaultable securities (DL Model) in [6] . Later, DL Model was generalized and the concept of counterparty risk which was from the default of firm’s counterparties was firstly introduced in [7] . Because it is impossible to assume that the impact of one firm’s default to another firm’s default keeps constant all the time, some authors introduced a hyperbolic function to reflect the attenuation effect in [8] . Recently, the cases that the interest rate satisfied the jump-diffusion process and the fractional Brownian motion were also discussed in [9] - [11] . The above conclu- sions on CDS were mostly obtained when the reference assets were the bonds.
With the rapid development of the financial securities and financial derivatives, the proportion of the financial assets in the total assets of the society is increasing. Therefore, the ability and the level of managing the risk for the financial institutions have become the decisive factors to improve their competitiveness and profitability. As a special enterprise, bank has a special role in the economical development. Its main business is to deposit and provide the loans. The credit risk of the bank is mainly derived from the loans. In China, credit risk is excessively concentrated. The existing methods and tools managing credit risk are ineffective. Thus, making use of domestic and foreign research on credit derivatives, the exploration and the development of credit derivatives to transfer credit risk in China’s market become very necessary. However, most conclusions on credit derivatives based on the loan were qualitative and there are few deeply quantitative research. [12] studied the pricing of mortgage CDS under structured model. [13] considered the characteristics in various types of loans. They proposed a new idea of using CDS to transfer their risks and gave the pricing model of CDS. The research on credit default swap based on the loan in foreign countries mostly used the reduced method such as [14] [15] . The above studies did not consider the contagious risk among the counterparties. [16] discussed the pricing problem of loan CDS with contagious risk. But the loan was particular in [16] and it had a cash deposit. In this paper, we will make use of the contagious model with attenuation effect to study the pricing of CDS based on fully amortizing fixed-rate mortgage (FRM). This kind of the loan is very common. Therefore, the conclusions in this paper will provide the theoretical preparation and the suggestions for the credit products development and the research in China.
2. The Structure of the Default and the Prepayment
Suppose be the filtered probability space satisfying the usual conditions.
be the filtered probability space satisfying the usual conditions. 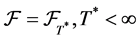
and Q is an equivalent martingale measure under which discounted securities’ prices are martingales and is
unique. The point processes 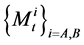 are the default processes of firm A and firm B and
are the default processes of firm A and firm B and  is the
is the
process of repaying the loan in advance of firm A and firm B. When 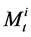 firstly jumps from 0 to 1, we call the firm i defaults and denote
firstly jumps from 0 to 1, we call the firm i defaults and denote 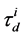 be the default time of company i. When
be the default time of company i. When  firstly jumps from 0 to 1, we call the firm i repays the remained loan in advance and denote
firstly jumps from 0 to 1, we call the firm i repays the remained loan in advance and denote 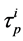 be the time of the repayment in advance.
be the time of the repayment in advance.  is
is
the indicator function, then  We assume that the unique macro state variable is the
We assume that the unique macro state variable is the
interest rate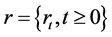 . Denote
. Denote
 (1)
(1)
where
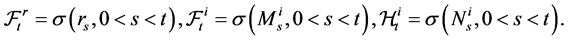 (2)
(2)
Let
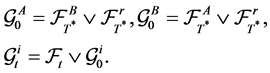 (3)
(3)
Suppose that 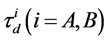 and
and 

and



We can define 


where 



The joint distributions of 


3. The Pricing of the Loan
The reference asset of credit default swap is a loan which takes the installments. After the signing of the loan contract, the borrower of the loan promises to repay equal amount of the principal and the interest to the lender in each repayment date which is called Fully Amortizing Fixed-rate Mortgage (FRM). Until the maturity date, the borrowers should repay all the principal and the interest. In addition, the lender generally requires the borrower to issue a corresponding collateral before the contract in order to improve the borrower’s credit rating and the credit limits. The collateral can be a basket of the financial assets or some physical assets. In this paper, we assume that the repayment of the loan satisfies two conditions: 1) The time of the payment is continuous; 2) Allow the borrower to repay the loan in advance, but need repay all the loans once time.
The borrower may choose to repay the loan in advance, default or hold a loan. We assume that L is the repayment amount of the borrower in the unit time. 











Therefore, the price of the loan is

Simplifying it, we have

where 


Lemma 1. For all 

Proof. The process in details can be found in Appendix.
In order to calculate the price of the loan, we give another form of the pricing formula (8).
Theorem 1. The pricing formula of the loan 

Proof. The process in details can be found in Appendix.
In the following, we give the primary-secondary model with the attenuation effect which the intensities of the default and the prepayment of firm A and firm B satisfy. We apply the contagious model into the loan and loan CDS based on the above loan.
Suppose that the default intensity and the intensity of repaying the loan in advance of the primary firm A satisfy the following equations:

the default intensity and the intensity of repaying the loan in advance of the secondary firm B satisfy the following equations:

where


Now, we assume that the interest rate satisfies Vasicek model,

where 



Let 



3.1. The Price of the Loan Issued by the Primary Firm A
In fact, we need to substitute (11) into the pricing formula in Theorem 1.
Firstly, we calculate

For any normal random variables X and Y,

So we obtain

Secondly, we calculate

then, we substitute (18) into (21) and get the value of
At last, we calculate

For any normal random variables X and Y,

Let 

and

Substituting (18), (24) and (25) into (22), we deduce the price of the loan issued by the primary firm A.
3.2. The Price of the Loan Issued by the Secondary Firm B
The pricing process is similar to the pricing of the primary firm A. We need three steps.
Firstly, we calculate

Let 

In the above equation, applying the integration by parts,

We assume that no defaults occur up to time t for firm A. Then

Substituting (29) into (28), we obtain

By (26),
(31)
Then, applying the conclusion that 
normal random variables X and Y, we have (31).
Secondly, we calculate

Because 
At last, we calculate

So

From above equation, we only need calculate 

The first part in (35) is similarly obtained by the same method and process to the former, so we omit it. Now,
we calculate the second part. Let 

where 




For 

Thus, combining (34)-(38), we deduce the pricing formula of the loan issued by secondary firm B.
4. The Pricing of Loan CDS
This paper assumes that the contract will terminate when the borrower defaults or prepays the loan in advance. We consider a simple situation that 




where
Firm C has a loan from firm J with the maturity date

The default intensity and the intensity of repaying the loan in advance of firm J satisfy the following equations

The default intensity and the intensity of repaying the loan in advance of firm K satisfy the following equations

Firstly, the time-0 market value of buyer C’s payments to seller K is

Secondly, the time-0 market value of seller K’s promised payoff in case of firm J’s default is

Let

Now, we calculate

Let






Then, we substitute (48)-(51) into (52) and get 




For any normal random variables X and Y,

Therefore,

We substitute (53)-(55) into(57) and get the above expectation.
Thus, in accordance with the arbitrage-free principle, we obtain the swap rate of loan CDS

5. Conclusion
CDS is one of the credit derivatives with large trading volume in the global financial market. In fact, there is a certain relationship among most of the companies in real market, such as the problem of holding each other’s bonds and so on. If a company defaults, it will affect the default possibility of another company. Default contagion is a common phenomenon in financial markets. This paper studies the pricing of CDS with the loan as the reference asset when contagious risk has the attenuation effect. We consider that the default intensity is correlated with the counterparty’s default and the interest rate following Vasicek model. The conclusions in this paper can provide the theoretical preparation and suggestions for the credit products development and the research in China. In fact, we only discussed the simple situation. The default of a firm and the prepayment of the loan issued by the firm are independent. Moreover, we price the loan and CDS under the primary-secondary framework. We can also consider other more complex cases, such as the correlation of the default intensity and the prepayment intensity, the looping default effect and so on.
Acknowledgements
We thank the editor and the referee for their comments. The research is funded by the National Natural Science Foundation of China (No: 11271259) and Funding scheme for training young teachers in Shanghai Colleges (ZZshjr12010). This support is greatly appreciated.
Cite this paper
Yinglin Liu,Ruili Hao,Zuhua Wang, (2016) Pricing Loan CDS with Vasicek Interest Rate under the Contagious Model. Journal of Mathematical Finance,06,416-430. doi: 10.4236/jmf.2016.63033
References
- 1. Merton, R.C. (1974) On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. Journal of Finance, 29, 449-470.
http://dx.doi.org/10.1111/j.1540-6261.1974.tb03058.x - 2. Duffie, D. and Singleton, K.J. (1995) Modeling Term Structures of Defaultable Bonds. Working Paper, Stanford University Business School.
- 3. Jarrow, R.A., Lnado, D. and Turnbull, S. (1994) A Markov Model for the Term Structure of Credit Risk Spreads. Working Paper, Conell University.
- 4. Jarrow, R.A. and Turnbull, S. (1995) Pricing Derivatives on Financial Securities Subject to Credit Risk. Journal of Finance, 50, 53-86.
http://dx.doi.org/10.1111/j.1540-6261.1995.tb05167.x - 5. Davis, M. and Lo, V. (2001) Infectious Defaults. Quantitative Finance, 1, 382-387.
http://dx.doi.org/10.1080/713665832 - 6. Jarrow, R.A. and Yu, F. (2001) Counterparty Risk and the Pricing of Defaultable Securities. Journal of Finance, 56, 1765-1799.
http://dx.doi.org/10.1111/0022-1082.00389 - 7. Bai, Y.F., Hu, X.H. and Ye, Z.X. (2007) A Model for Dependent Default with Hyperbolic Attenuation Effect and Valuation of Credit Default Swap. Applied Mathematics and Mechanics (English Edition), 28, 1643-1649.
http://dx.doi.org/10.1007/s10483-007-1211-9 - 8. Hao, R.L. and Ye, Z.X. (2011) The Intensity Model for Pricing Credit Securities with Jump-Diffusion and Counterparty Risk. Mathematical Problems in Engineering, 10, 1-16.
http://dx.doi.org/10.1155/2011/412565 - 9. Hao, R.L., Liu, Y.H. and Wang, S.B. (2014) Pricing Credit Default Swap under Fractional Vasicek Interest Rate Model. Journal of Mathematical Finance, 4, 10-20.
http://dx.doi.org/10.4236/jmf.2014.41002 - 10. Gu, W.J., Liu, Y.L. and Hao, R.L. (2016) Attenuated Model of Pricing Credit Default Swap under the Fractional Brownian Motion Environment. Journal of Mathematical Finance, 6, 247-259.
http://dx.doi.org/10.4236/jmf.2016.62021 - 11. Wu, S. and Liang, J. (2011) Valuation of Mortgage Loan CDS. Applied Mathematics: A Journal of Chinese Universities, 26, 269-278.
- 12. Zhang, X.Y. (2012) The Pricing of Credit Default Swap Based on Project Loans. The Dissertation of Nanjing University of Science and Technology, Nanjing.
- 13. Howard, S., Shunichiro, U. and Zhen, W. (2007) Valuation of loan CDS and CDX. Working Paper, Stanford University.
- 14. Zhen, W. (2007) Valuation of Loan CDS under Intensity Based Model. Working Paper, Stanford University.
- 15. Hao, R.L., Zhang, J.Q., Liu, Y.H. and Hu, Z.H. (2016) Pricing Credit Default Swap with Contagious Risk and Simulation. Shanghai Jiaotong University (Science), 21, 57-62.
- 16. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654.
http://dx.doi.org/10.1086/260062
Appendix
1. Proof of Lemma 1
Proof. Firstly, from Section 2, we have

Similarly, we have

2. Proof of Theorem 1
Proof. Firstly,

Secondly,

At last,

Therefore, the theorem is deduced.
NOTES
*Corresponding author.















