Received 12 May 2015; accepted 14 February 2016; published 17 February 2016

ABSTRACT

This paper is devoted to the connection between the probability distributions which produce solutions of the one-dimensional, time-independent Schrödinger Equation and the Risk Measures’ Theory. We deduce that the Pareto, the Generalized Pareto Distributions and in general the distributions whose support is a pure subset of the positive real numbers, are adequate for the definition of the so-called Quantum Risk Measures. Thanks both to the finite values of them and the relation of these distributions to the Extreme Value Theory, these new Risk Measures may be useful in cases where a discrimination of types of insurance contracts and the volume of contracts has to be known. In the case of use of the Quantum Theory, the mass of the quantum particle repre- sents either the volume of trading in a financial asset, or the number of insurance contracts of a certain type.

Keywords:

Hamiltonian, Eingenvalues, Continuous Spectrum, Quantum Risk Measure

1. Introduction

As it is mentioned in [1] , the cause for the use of the use of quantum theory in risk models and finance is their complexity, in the sense that the return of an asset or the value of it depends on several factors. At this point we may quote that though there exists a broad literature in finance which relies on the notions of quantum mechanics, there is a lack of literature which connects quantum mechanics’ modelling and risk theory. A semi- nal reference in quantum finacnce is the paper under the same title [2] , which refers to the basics of this subject. Another essential reference is [3] , which is more related to asset pricing. The other book [4] by the same author is related to interest rates and bond pricing. We write this paper in order to contribute in the research on the relation between quantum finance and risk theory where there is not so much literature. A central role in the theory of risk models recently belongs to the risk measures. Since the main objective of this paper is the risk measures on Hamiltonian operators, it is useful to remind some essential notions from quantum theory, which are useful in the sequel (see [5] ).

Definition 1.1. An operator A on a Hilbert space 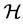is called symmetric if for any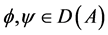, where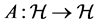, the relation

holds.

Definition 1.2. An operator 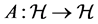is self-adjoint, if.

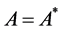Definition 1.3. A Weyl sequence for the operator A and the eigenvalue 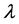is a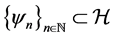, such that

,.

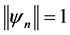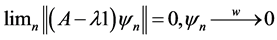Definition 1.4. The continuous spectrum of an operator A is the set of the eigenvalues 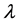of A, where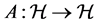, such that there exists a Weyl sequence for A and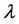. The set of these eigencalues is denoted by.

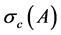Definition 1.5. The point spectrum of an operator A, where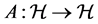, is the set of isolated eigenvalues of A having finite multiplicity. It is denoted by.

Definition 1.6. (Weyl’s Theorem) If, for the spectrum of A, the following relation holds:

In the case of the one-dimensional quantum models and the Hamiltonian operator , where denotes the Laplacian, while moreover for the potential is a continuous function, such that, then H is self-adjoint and. Hence, since the Hamil- tonian has surely positive eigenvalues, the question is whether according to the form of the distribution which arises from, the infimum of the continuous spectrum is greater than zero (denotes the time- independent wave-function). The fact that Hamiltonian is self-adjoint implies that

for any wave function which is a solution of the time-idependent Schrödinger Equation. The paper is organized as follows. In the next section, we mention the relation between the main notions of the quantum mechanics and the risk theory and finance as well. We emphasize on the role of the wave-functions as probability- density producers related to the claim of some insurance contract. We also define the notion of the quantum risk measure, related to the time-independent Hamiltonian associated to the specific family of distributions. We finally provide the Pareto and the Generalized Pareto as examples of families which verify that such risk measures take finite values.

2. On Quantum Risk Theory

The elementaries of quantum finance denote that any asset is a quantum particle, whose changes in position x correspond to the changes of its value. The changes of its value are decomposed into the kinetic energy of the particle, which is the total effort of the investors to change its value. For this reason, the mass m of this particle, denotes the total number of investors which are involved into investements to this asset. On the other hand, the dynamic energy denotes the changes of the value whose cause is some exogenous factor being a function of the position x of the quantum particle. This is the meaning of the function of the potential. Hence the one-dimensional Schrödinger Equation (S.E.)

of the Hamiltonian’s Spectrum, denotes that the set of the possible Asset Monetary Values is the set of the Hamiltonian’s Spectrum (denotes the Planck Constant). We also remind that

which denotes that any wave-function is a squarely-integrable function. By the term wave-function we mean any solution of the above time-independent Schrödinger Equation. Every wave-function corresponds to a probability density, or a positive multiple of. A linear combination of Hamiltonians with continuous spectra, corresponds to a portfolio of assets. This portfolio may include the identity operator, which denotes the riskless asset. In classical Quantum Theory, wave-functions of the Continuous Spectrum are not squarely integrable, because they probably do not correspond to a real quantum physical phenomenon, while we indicated that Hamiltonian Operators do have this property, since the time-independent Hamiltonian is self- adjoint. In this paper, we further investigate which is the form of the potential function, under which the S.E. is solvable under precific distribution functions provided by the wave-functions. We also notice that in this case, the Hamiltonian is self-adjoint and symmetric, since we refer to the time-independent Hamiltonian, or else we have that, in terms of brackets

In this paper we prove an essential Theorem on what it may be called Quantum Risk Theory. This Theorem refers to any family of distributions, which is consisted by densities of the form, where is some parametric space. If the support of any density of the family is for

the form, and for the function,

then:

1) If, then for any value, and for the Potentital Function

the wave-function for the eigenvalue is a solution of the Schrödinger Equation S.E.

2) The Spectrum of the Hamiltonian and the values of the support of the density of the probability for the position of the quantum particle, if, coincide.

3) The associated Coherent Risk Measure takes a finite value, being equal to the minimum value of the support.

4) The brackets are equal to zero.

We also give specific Examples of classes, mainy inspired from Extreme Value Theory, since the additional capital requirement functionals are more sufficient in these cases. We also present the Pareto Distri- butions and the Generalized Pareto Distributions as Examples of applications of the previous Theorem. The mass of the quantum particle may be estimated from the volume of the investors to the certain asset, in the financial case. Of course, the historical data―which, in the financial case they take a daily form―about this volume have to be fitted to some distributions. For this reason, one of the well-known non-parametric tests, like Kolmogorov-Smirnov ( [6] ) or Anderson-Darling ( [7] ), may be used. In the sequel, random data from the fitted distribution may be produced and the Monte-Carlo estimator of the mean volume of investors has to be compared to the historical estimation of the mean volume. This model may be also interpreted as a model of insurance, especially in cases where there is not any other well-known mathematical model for the premium calculation, for example in naval insurance. This interpretation is actually a more adequate motivation, since we refer to heavy-tail distribution families like the Pareto and the Genaralized Pareto. In this case the mass of the quantum particle may denote the volume of the insurance contracts of a certain type adopted by the insurance company. In order to be accurate, for a specific value of the parameter, the wave functions except are not of special importance. We formally deduce orthogonality under different eigenvalues in order to fit the frame of Quantum Theory. The important is that Quantum Theory provides a way to calculate finite insurance premia for the associate risk measures in the cases where the supports are represented in the way. For a reference to the Mathematical Formulation of Quantum Theory, we refer to [5] . For a finite- dimensional model of quantum mechanics in finance, see [1] . An interesting point is that in ( [8] , Ch. 2), the power-law tails, which denote the Pareto distributions are mentioned, but without the whole analysis we made here.

3. Static Quantum Risk Measures

Under the above frame, for a Hamiltonian H associated with a continuous spectrum, or else the set of the eigenvalues of H contain an open set of, we take the following Quantum Risk Measure, associated to the Hamiltonian H:

where denotes the spectrum of the Hamiltonian H, if denotes some normalized wave-function.

The above theorem is essential:

Theorem 3.1. If S(H) contains an open set of R, then the quantum risk measure is coherent.

We remind that the Hermitian identity operator, being defined on the real line, has the following property:. This operator stands for the riskless asset.

Proof. We verify the four properties of coherence.

1), because since, but

, hence Translation Invariane holds.

2) Two assets coincide with two Hamiltonians, which by assumption do have continuous spectra on. Subadditivity arises from.

3) The Positive Homogeneity arises from the fact that for any specific,

.

4) Finally, the Monotonicity arises from the fact that if for two Hamiltonians the property

holds for any, then. □

4. The Essential Theorem

Theorem 4.1. Consider a family of distributions, which is consisted by densities of the form, where is some parametric space. If the support of any density of the

family is for the form, and for the function,

then:

1) If, then for any value, and for the Potential Function

the wave-function for the eigenvalue is a solution of the Schrödinger Equation S.E., where the Potential Function for is equal to zero.

2) The Spectrum of the Hamiltonian and the values of the support of the density of the probability for the position of the quantum particle, if, coincide.

3) The associated Coherent Risk Measure takes a finite value, being equal to the minimum value of the support.

4) The brackets are equal to zero (the denote different eigenvalues of the Hamiltonian).

Proof. 1) For the function, since,.

2) in this case, which is actually the support of.

3) = sup{{ is a normalized eigenfunction of H} = -inf{E|E is an eigenvalue of H}.

4)

Hence, if,. □

Examples

Example 4.2. The Pareto Family of Distributions

. The support of the density is of the form.

Also if, if we pose, for a specific value of the parameter. In this case

Example 4.3. The Generalized Pareto Family of Distributions

. We take the case where support of the density is of

the form. If, then

5. Conclusion

The conclusion of the paper is that the notion of risk measure may be extended in a quantum finance framework, as far as it may be applied on a time-independent Hamiltonian operator and specifically on its continuous spec- trum. The value of such a risk measure is finite and in the case of Pareto and Generalized Pareto distributions is negative. This risk model may be applied either in the case of reinsurance pricing, or in the case where no other known model is developed like naval insurance contracts.

Cite this paper

Christos E.Kountzakis,Maria P.Koutsouraki, (2016) On Quantum Risk Modelling. Journal of Mathematical Finance,06,43-47. doi: 10.4236/jmf.2016.61005

References