Received 18 April 2015; accepted 26 July 2015; published 30 July 2015

ABSTRACT

We look at the price of the European call option in a quanto market defined on a filtered probability space 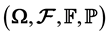when the exchange rate is being modeled by the process 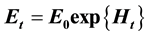where 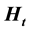is a semimartingale. Precisely we look at an investor in a Sterling market who intends to buy a European call option in a Dollar market. The market consists of a Dollar bond, Sterling bond and and Sterling risky asset. We first of all convert the Sterling assets by using the exchange rate 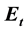and later on derive an integro-differential equation that can be used to calculate the price on the option.

Keywords:

Semimartingale, Hedging, Arbitrage, Contingent Claim

1. Introduction

This paper considers the European call option in the Black-Scholes market when the exchange-rate is a semimar- tingale. Specifically, we consider a problem of a Dollar investor seeking to invest in a Sterling market. Theory of exchange rates has been widely discussed (see [1] -[4] ). Exchange rates change with time due to a number of factors, such as changes in fiscal and monetary policies, interest rate differentials between two countries usually resulting in revaluation or devaluation of currency. The main challenge is to construct a model which captures the dynamics of exchange rate and its effect when investments are made in different currencies. A number of models have been developed which are being modified to accommodate reality. Generally, exchange rate models fall into two major categories: Those that treat the dynamics of exchange rate as a continuous process and those treat exchange rates as processes with jumps. The Black-Scholes model is the most celebrated non- jump model whose dynamics are modelled by the stochastic differential equation 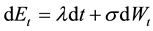where 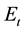is the exchange rate, λ is the drift parameter, σ is the volatility parameter and W_t is a Wiener process. This model assumes the logarithmic exchange which follows Brownian motion with drift. Using this as a benchmark model,

other models were developed, for example, a model given by the equation

where is a pair of correlated Brownian motions with correlation co-efficient ρ and

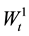is Brownian Motion driving the given asset prices [2] . It is known that jump-diffusion models are more realistic for studying the dynamics of exchange rates [3] . Dating back from the introduction of jump-diffusion process by [4] [5] as a tool for modelling the prices of options based on more general processes of underlying asset returns, jump-diffusion processes have also been widely used in modelling the dynamics of exchange rates. Empirical evidence based on simple jump-diffusion models suggests that jumps really form significant com- ponents of foreign exchange rate processes [1] [3] . As such, it is reasonable that both empirical and theoretical studies of exchange rates under uncertainty should allow for the presence of discontinuities explicitly. There has been a wide use of jump-diffusion processes to model financial time series to reflect discontinuities of asset returns. Some of the most well known jump-diffusion models for the dynamics of foreign exchange include: 1) Merton’s Jump Model, 2) Conditional Heteroscedasticity and Jump model and Mean-Reversion, Conditional Heteroscedasticity and Jump model. The Merton’s Jump Model is given by the stochastic differential equation 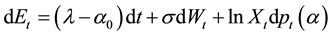where E_t is the exchange rate, λ_t is the instantaneous expected return, σ is the instantaneous volatility of the asset’s return subject to the Poisson jump not occurring, W_t is the Gauss- Wiener process, 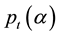is a Poisson process which is independent and identically distributed over time, α is the intensity parameter of Poisson distribution, 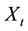is the random jump size with 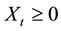and, 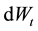are statistically independent. This model explicitly allows for the presence of asymmetric lognormal jumps to the exchange rate. 3) The Conditional Heteroscedasticity and Jump model, is described by the stochastic dif- ferential equation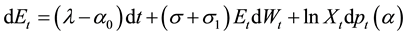, which is an extension of Merton’s model and allows for conditional heteroscedasticity in addition to jumps. 4) Lastly, the Mean-Reversion, Conditional Heteroscedasticity and Jump model, described by the differential equation where. This model has a linear drift term in E_t which makes it possible to capture the mean-reversion feature of the underlying process in addition to conditional heteroscedasticity and asymmetric jumps. The aim of our work is to provide further evidence for appropriateness of jump models. We do that by formulating an exchange rate model in terms of the general semimartingale on filtered probability space to model the dynamics of the exchange rate where. Our approach leads to general formulae which capture both the continuous and jump-diffusion cases models depending on whether, the continuous model or, the jump diffusion one. The approach utilizes the specific market model called the Black-Scholes Quanto model, in other words, we consider products denominated in a currency other than those in which they are traded. Our prime interest is to price the claim C_T, which in our case is the European call option, in this market when the dynamics of the exchange rate is being modelled by the general semimartingale as described above.

2. The Model

We consider the quanto market model consisting of Dollar bond, Sterling bond, Sterling risky asset price and the Exchange rate on the filtered probability

space where, and, is the natural filtra-

tion generated by the stock price process while, is the natural filtration generated by the exchange rate process. describes information about prices and the exchange rate revealed to investors. We assume that the probability space satisfies the usual conditions i.e the σ-field is -complete and every contains all -null sets of. is the Brownian motion in- dependent of and i.e is a cadlág process that admits the decomposition where (a process of bounded variation), and. For a dollar investor in the quanto market defined in this problem, we want to find what is the price of the European call option having strike price k and strike time t?

Converting into Dollars

Since our asset is in Sterling, we need first of all to find the Dollar equivalent of this asset. For convenience sake we let. be the dollar value of the Sterling asset price given by

(1)

Define

(2)

where

(3)

is a semimartingale since it is the sum of two semimartingales and. This in turn implies that is a semimartingale. Let

Then, using Ito’s formula for semimartingales [6] [7] , the dynamics of the dollar value for the Sterling risky asset is

(4)

where

(5)

(see Appendix). Let so that then and

being a semimartingale has the form

(6)

It is important to take note that superscript in is used to stress that is the martingale part for process which in this case

(7)

Since is a local martingale, it can be decomposed as

(8)

where is the continuous part and is the discontinuous part of. For more details and a proof of Equation (8) see [8] . Since, we have. From Equation (6), we have. Similarly if we let to be the continuous martingale part of then

(9)

Now, using the bilinear property of sharp bracket process [9] , we obtain

(10)

We further note that

This is true because μt, and σW_t are continuous processes. It then follows that

(11)

Substituting X_t and Equations (3), (10), (11) into Equation (5) we have

(12)

Similarly, let Z_t be the dollar value of the Sterling bond given by

Let

(13)

It clearly follows that

(14)

Noting that

(15)

Note that Equation (15) follows because us is a continuous function so that. The continuous martingale part of is

Hence

Z_t can now be written as

Its differential form, the dynamics of the dollar value of the Sterling bond can be written as

Which can be written as

(16)

where

(17)

And

For our analysis, we need to express the decompositions (Equation (12)) and (Equation (17)), in stochastic integral form, hence we use the random measure of jumps.

In our case, we have

(18)

And from Equation (10) we have

Hence, process of bounded variation can be express as

(19)

where A is as defined in Equation (6) and D is the process of bounded variation for the semimartingale H_t. We can express these results in canonical form by using the random measure of jumps (see [7] ). From Equation (5),

(20)

Now, if we assume that, then

(21)

where

(22)

Now if we substitute Equations (9) (10) and (19) into Equation (21) we obtain

(23)

where

(24)

i.e.

(25)

where and is a predictable process. Similarly from Equation (13)

If we set with as a truncation function, we have,

, and together with Equation (17),

(26)

where

This means the dynamics in our market model are modeled by the equations can also be presented by the eququations

(27)

where and are as defined in Equations (21) and (26) respectively. Before we proceed we need to show that our market model defined by the system of Equation (27) does not entertain arbitrage opportunities.

3. Arbitrage

A question we must ask before we proceed is whether the market (27) allows arbitrage opportunities or not. In this market, an investment strategy or portfolio is a predictable process

(28)

Such that

(29)

denote the fractions of total wealth invested in B, z, and Y respectively at time t. The condition in

inequality (29) ensures that the integrals make sence and are is a martingales.

Let

(30)

be the worth the worth process. We need to know if our portfolio is self-financing. A portfolios is self-financing if can also be written as

(31)

or in differential form, if

(32)

Equations (31) and (32) imply that the portfolio is self-financing if changes in the value of the portfolio on an infinitesimal interval are due entirely to the changes in value of assets and not to an injection (or removal) of wealth from outside.

To show that our portfolio is self-financing, we use Lemma (5.1.3) in [2] . According to [2] , is a self- financing portfolio if

(33)

where, the discounted value of the wealth process.

This means

(34)

Satisfying Equation (33). Hence is a self-financing portfolio. If in additional to this to (34),

as defined in Equation (34) above is lower bounded, then is said to be admissible. It is written as.

If is not admissible, it is not hard to construct doubling strategies, that is, a portfolio that attains arbitrarily large values of wealth with probability one when, starting with zero initial capital at, a situation we are avoiding. We first of all show that in this market, is an admissible strategy. The dynamic for the dollar value of the sterling bond is given by the equation

Similarly, the dynamic for the dollar value of the Sterling risky asset is given by the equation

From Equation (30)

(35)

Since the portfolio is self-financing (Equation (32)), then

Then

This means the differential form of of the dynamics of the discounted wealth process is

Hence the discounted wealth process will be

From the above equations, is a lower bounded process. It follows that is lower bounded implying that is an admissible strategy.

Definition 1 A portfolio is called arbitrage if

(36)

Since the portfolio in our market is admissible, we really claim there are no arbitrage opportunities in the market. The following discussion is a build up towards the proof to justify this claim.

3.1. Converting Y_t into a Martingale

Our stock price process as described in Equation (27) is a semimartingale. To use the martingale approach, we need to convert the price process into a martingale by finding another probability space equivalent to our probability so that Y_t becomes a martingale. Now we consider our price process

(37)

(see Equation (27)). and with Equation (2), we can say

(38)

This means our price process is a local martingale iff is a local martingale. Now () becomes a local martingale through the change of probability measure theorem for semimartingales i.e. we find another measure under which Y_t becomes a martingale. To achieve this, we consider the following:

Suppose we have the triplet for a semimartingale x under measure what are the triplets for semimartingale under a new probability measure?

Using the Gisanov’s Theorem for semimartingales,

(39)

where satisfies the equation

(40)

And is defined by the equation

(41)

where is the positive measure on de- fined by

(42)

where is a nonnegative function on (for see [8] ). is, by

definition, the -a.s unique -measurable function with property

(43)

For all non-negative -measurable functions. This means that under measure, the semi- martingale process evolves according to the equation

(44)

where

(45)

And

(46)

is a -Brownian motion [10] .

We start by finding the values β and for our case. To do this we first find, the continuous martingale part for the risky asset process Y_t, as described by Equation (2). Using Itó’s formula for semimartingales, we have

It is easy to see that the continuous part of the semimartingale is given by

(47)

Hint: in our calculations, we have made use of Equation (2) and the canonical decomposition of the semi- martingale hence the differential form of in our case can be written as

(48)

From Equation (47) and using properties of conditional quadratic variation process for stochastic integrals with respect to semimartingales

(49)

Now

(50)

We can deduce from equating Equations (49) and (50), that Equation (40) can only hold if, which is adopted as our choice of in this study. From the Equation (43) given by

And the Equation (42) which simplifies below

We arrive at a choice of given by

(51)

Hence from Equation (46)

(52)

Now under

(53)

(see [8] )

From Equation (44),

(54)

But in our case, to really achieve the case, we make the following assumption: The process has bounded variation. Provided this assumption holds and that the conditions of lemma (2.13) in [11] are satisfied, then

(55)

It is also important to take note that from the assumption we have made and lemma (2.13) in [11] above, is exponentially special i.e. is a special semimartingale. Now

(56)

(see [12] ) and from Equation (55)

(57)

From Equation (38)

(58)

This means that under

(59)

Which is a martingale process.

This means that since our market has an equivalent local martingale measure then by by the First Fundamental Theorem of Asset Pricing, there is no arbitrage in our market model ([13] ).

3.2. Equivalent Local Martingale Measures (ELMM)

In our previous section (section 3.1), we have proved the existence of ELMM and hence that the market is arbitrage free. But the question we really need to ask is whether or not is a unique measure.? One of the major problems of financial markets with jumps is that they are typically incomplete. The martingale measure is no longer unique as compared to complete market situation and in this case different martingale measures lead to different strategies. There are more than one ELMM, in fact infinitely many. The question is that which one of them should one use in the pricing formula. To answer our question it turns out that there is a minimal entropy martingale measure such that the optimal strategy for can be computed in terms. The following discussion gives the definition of minimal martingale measure.

Minimal Relative Entropy Martingale Measure (MEMM)

Let be a set of all equivalent martingale measures of.

Definition 2 is said to be minimal entropy martingale measure (MEMM) of if it satisfies the follow- ing formula

where is the relative entropy of, which is given by the following formula

(60)

(see [14] [15] ).

The relative entropy measures the minmal departure from a given measure. The relative entropy is always non-negative and is equivalent to.

The minimal martingale measure is uniquely determined as discussed in [14] [15] .

Let be as defined in Equation (28). We assume that the process is pre- dictable while and are adapted. Hence Equation (37) takes the form

(61)

where is now a martingale.

Now solving (61) above gives

(62)

where is the Dolĕans Dade stochastic exponential.

Now

(63)

And

(see Equation (10)). Hence

(64)

(for compare with Equation (13), page 666 in [7] )

Hence

(65)

The process, in Equation (65) above, is a martingale and it is under a new probability measure. This equation marks one of the major contributions of this study to the the theory option pricing through martingale approach in the sense that it accommodates both continuous and jump cases. In the situation where, then and Equation (65) becomes

(66)

which is the continuous and most familiar case, while if then we have a jump case. The equation brings with it the convenience of converting the stock price into a martingale whenever we are using a martingale approach as in any of the cases, the process of converting the process into a martingale, simplifies to mere calculation of, and and substitute into Equation (65).

3.3. The Price of European Call Option

We now come to the question fundamental of this study.

How much should the investor be willing to pay for a European call option at t = 0 in the case where Y_t is a semimartingale process as defined in Equation (65)?. We extend the theorem which was given in [16] .

Theorem 1 Let, with its canonical decomposition as shown in Equation (59) above, be a process with independent increment, and assume that, and exist where. Then the following integro-differential equation holds:

(67)

Proof. Before we proceed, we take note of the following:

This means that where

The theory of pricing of the European call option (see [17] ) and the Markovian property of, the value of the European call option at time T is given by

where is given by

□

But how do we evaluate the value in our case. By using the Markovian property of we applying Ito’s formula to and obtain

Now using the fact that a predictable local martingale with finite variation starting at zero is zero (theorem leads us to the equation i.e.

4. Examples

4.1. Example 1: Continuous Case

Suppose

From Equation (3),

(68)

where is the Brownian Motion on the same stochastic basis as Brownian Motion and that these Brownian Motions are correlated with correlation co-efficient ρ. Obviously, from Equation (68),.

(69)

Note that U, as it is defined in Equation (69), is an element of Borel sets which do not have a 0 element. Since and 0 cannot be an element of u justifies Equation (69).

It follows that

(70)

Similarly

(71)

From Equations (39) and (51)), under measure,

(72)

And. Hence from Equation (64)

Hence, and. Using theorem (1) with and leads to equation

(73)

And hence (from the same theorem)

(74)

4.2. Example 2: Process with Jump

Suppose in our model, the exchange rate is not continuous and is modeled by the stochastic differential equation

(75)

where is the -Brownian Motion process, M_t is the compensated -martingale process associated with the Poisson process N_t (with intensity) i.e. and is independent of the Brownian motion N_t. We choose to be a Gaussian process with independent increments, independent to both and N_t. We let and. Assume that, ,. We further assume that is inde- pendent of W_t where W_t is the Brownian motion as defined in Equation (3).

To find out what our X_t and, are in this case we first of all solve our equation.

(76)

Using Itó’s formula for processes with jumps, we let

From which we obtain

And

(77)

Hence from Equation (77), we obtain given by

Clearly, (since). From Equation (2), we obtain

(78)

From (78) we obtain the process of the form

(79)

Equation (79) yields the sharp bracket process for of the form

And hence under measure,

(80)

Clearly (80) is a process with independent increments (as it is the sum of processes with independent increments), hence we can find a deterministic function, a deterministic measure-valued function and a deterministic increasing function such that, (Jacod and Shiryaev [8] ). is also a Lèvy process , we can choose, c to be a constant and (the Levy measure) (see section). In addition, where and is the distribution of the jump size of less than 1, i.e. from this we can deduce that the expected number of jumps, in time interval 1 is and the jump size is distributed according to F. If we let then. Since is a Gaussian process with and, Then

And

From Equation (80),

And

(81)

Hence from theorem (1), is found by solving the equation

(82)

And

4.3. Example 3: H_t a Cumulative Process

We consider a situation where the exchange rate is where and are independent processes. In this case. This means that

In this case

This means that

Hence Equation (80) becomes

(83)

This means is the solution of the integro-differential equation

(84)

With

5. Discussion

Equation (73) compares well with Equation (82) in the sense that (82) without the term

(85)

Gives Equation (73). This means that Equation (85) is the contribution of the jump to the price of the option. The effects of the jumps on the price of the the option can be easily observed from this Equation (82) through the role, which is the jump parameter in this equation. For example in the case where, we

Hence Equation (82) is reduced to Equation (73) which is a continuous case. This can be further justified from the definition of our. and hence i.e. if, justifying why case (2) in section (4.2) is reduced to case (1) in section (4.1) and at the same time confirming why Equation (82) degenerates to equation (73). We also take note that the co-domain of the function is. This means is not taking negative values hence has a positive effect to the value of the option. The positive effect of is in the sense that as far as

In Equation (82), the increase in will mean the increase in the price of the option In the same vein, depends on as hence we expect as takes positive values. This means has a positive effect in Equation (82), emphasizing the effects of.

We also take note that expression (85) is also equal to zero if either (the case which we have just discussed), (the same case since (in our case) if and only if) or if

A case which can be handled numerically.

6. Conclusion

The method gives the general method of calculating the price of the option in the sense that it accommodates both continuous and processes with jumps. When, we are talking of continuous processes as shown by example 1 and when we are talking of processes with jumps. This can provide a more general way of finding the price of an option.

Cite this paper

E. R.Offen,E. M.Lungu, (2015) Pricing a European Option in a Black-Scholes Quanto Market When Stock Price is a Semimartingale. Journal of Mathematical Finance,05,286-303. doi: 10.4236/jmf.2015.53025

References

Appendix

Then, using Ito’s formula for semimartingales (Protter [6] ), we have

(86)

And in differential form, this can be expressed as