Received 22 January 2015; accepted 10 February 2015; published 13 February 2015

ABSTRACT

We consider a rating-based model for the term structure of credit risk spreads wherein the credit- worthiness of the issuer is represented as a finite-state continuous time Markov process. This approach entails a progressive drift in credit quality towards default. A model of the economy is presented featuring stochastic transition probabilities; credit instruments are valued via an ultra parabolic Hamilton-Jacobi system of equations discretized utilizing the method-of-lines finite difference method. Computations for a callable bond are presented demonstrating the efficiency of the method.

Keywords:

Optimal Stopping, Failure Rate, Regime Switching, Credit Risk Spreads

1. Introduction

When pricing of credit instruments subject to default risk, market participants typically assume that default is unpredictable, using dynamics derived from rating information in order to take advantage of credit events (cf. [1] ). Generally, they fall into a loose hierarchy known as reduced-form models. The most ubiquitous approach involving hazard rate models wherein default risk via unexpected events is modeled by a jump process. In this framework, credit-risky securities are priced as discounted expectation under the risk neutral probability mea- sure with modified discount rate (cf. [2] , [3] ). Although conceptually simple and easy to implement, these models are limited by the appropriate calibration of the hazard rate process. More generally, spread modeling represents spreads directly and eliminates the need to make assumptions on recovery (cf. [4] , [5] ). Finally, rating based models consider the creditworthiness of the issuer to be a key state variable used to calibrate the risk-neutral hazard rate (cf. [6] - [8] ). A progressive drift in credit quality toward default (an absorbing state) is now allowed as opposed to a single jump to bankruptcy, as in many hazard rate models. Rating based models are particularly useful for the pricing of securities whose payoffs depend on the rating of the issuer.

In this paper, we consider a rating based regime switching model for the term-structure of credit risk spreads in continuous time (cf. [9] , [10] ). A unique feature of our model is the inclusion of stochastic transition pro- babilities. Credit instruments are then characterized as the solution to a ultraparabolic Hamilton-Jacobi system of equations for which we develop a methods-of-lines finite difference method. Computations are presented for a rating based callable bond which validates the applicability and efficiency of the method.

2. Model of the Economy

In this section, we introduce the dynamics of the risk-less and risky term structures of interest rates as well as the bankruptcy process. To this end, we assume the existence of a unique equivalent martingale measure such that all risk-less and risky zero-coupon bond prices are martingales after normalization by the money market account (cf. [11] , [12] ). Without loss of generality, we suppose a single risky zero-coupon bond price and continuous trading over a finite time interval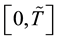. We let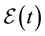 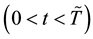denote a continuous time Markov process on the regime (or états) space 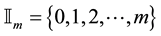with associated transition probabilities

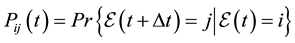, for all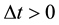; it follows that

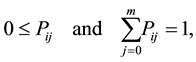(2.1)

for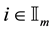. Let 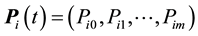represent the 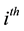-state transition distribution.

We define the transition probabilities as follows. The 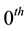-state we associate with default, in which case 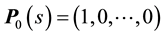. For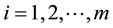, we define the 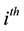-state transition dynamics consistent with the non- negativity constraint in (2.1) such that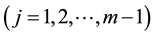

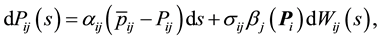(2.2a)

(2.2b)

for, where

and is the mean transition level satisfying, is the rate of reversion to the mean,

and is a Wiener process. From (2.1), it follows that and so

(2.2c)

(2.2d)

We relate the transition matrix to the regime dynamics via the infinitesimal generator,

such that

for, and

where is the vector of probabilities. Without loss of generality, we associate with the vector, , , , subject to the dynamics

(2.3a)

(2.3b)

for, where is a martingale with respect to the filtration generated by and

( [13] , Chap 4.8; [14] , Part III, App. B; [15] , Chap 8). In particular, the state of the system

is known at inception such that, for some.

We suppose that the risky interest rate R follows a state specific Cox-Ingersall-Ross dynamic given by

(2.4a)

for, with mean reversion level and rate of reversion to the mean, such that

(2.4b)

where is a Wiener process. In default, otherwise and. The risky bond price associated with a maturity satisfies

(2.5a)

(2.5b)

We consider the risk-less interest rate to satisfy

where in default for convenience, and otherwise.

For a given contract, we define the value function associated with the joint Markov ultradiffusion process (2.2)-(2.5) such that

(2.6)

for, where.

In particular, for a non-coupon paying bond and otherwise, where is the de- fault recovery rate, whereas for a callable bond and other- wise, for some rating based exercise price. Generalization of (2.6) and the subsequent analysis to include early exercise features follows routinely and will not be considered here.

3. Characterization

Letting and

(3.1a)

we recover (2.6) succinctly as

(3.1b)

for. By Itô’s rule, the value function (2.6) is characterized via (3.1) as the solution to the ultraparabolic Hamilton-Jacobi system of equations

where

Let denote the temporal variable and

the spatial, we define

and, such that the above can be written

(3.2a)

for all, subject to the terminal constraint

(3.2b)

for, where

4. Approximation Solvability

Towards obtaining a constructive approximation of (3.2), we consider an exhaustive sequence of bounded open domains such that and as well as a sequence of monotonically increasing real numbers, as. Let and, we seek satisfying

(4.1a)

for all, subject to the boundary condition

(4.1b)

for, and terminal constraint

(4.1c)

where. As (3.2) is an infinite horizon problem in, we remark to the necessity of intro- ducing the artificial terminal condition along the frontier (cf. [16] ). In particular, as, on any compact subset of, for any fixed.

We next place (4.1) into standard form by setting, , , in which case. Letting

Equation (4.1) becomes

(4.2a)

for all, subject to the boundary condition

(4.2b)

for, and initial condition

(4.2c)

where, where.

We consider the discretization of (4.2) by the backward Euler method temporally and central differencing in

space. To this end, we introduce the temporal step sizes and mesh sizes, such

that and. Spatially, we utilize the step sizes and mesh sizes

; we denote the value of on the grid by

where, , , , and so forth. Notationally, we let

, where, , , and

. For

the difference quotients are then backward first order in time:

and central second-order in space:

and so forth, and

and so forth.

Given the above, we define the method-of-lines finite difference discretization of (4.2) such that

(4.3a)

for all, subject to the boundary condition

(4.3b)

for, and initial condition

(4.3c)

where, ,

and. We solve (4.3) utilizing the pseudo-code (cf. [16] , [17] ):

do

do

solve for via (4.3).

5. Numerical Experiment

In this section, we present a representative computation for the valuation of a callable bond relative to three credit ratings:

and rating’s dependent pay-off contract

with expiry. We suppose a solvent risk-free rate of return of. For simplicity, we will con- sider the following transition matrix

in which only the default probability is stochastic.

For, we have the economy;

(5.1a)

(5.1b)

(5.1c)

where

and

Letting and, the ultraparabolic Hamilton-Jacobi system of Equations (4.1) for the value function associated with the ultradiffusion (5.1) is then

(5.2)

for all,

(5.3a)

for all, such that

(5.3b)

for and

(5.3c)

(5.3d)

and

(5.4a)

for all, such that

(5.4b)

for and

(5.4c)

(5.4d)

Figure 1 and Figure 2 show the value function components and, respectively, for. Relative to the discretization of (5.2)-(5.4), we utilized, , ,. In particular, we note the effect of the rating based exercise prices on and and the de- creasing value of with increasing, as expected.

Cite this paper

SeungmookChoi,Michael D.Marcozzi, (2015) A Regime Switching Model for the Term Structure of Credit Risk Spreads. Journal of Mathematical Finance,05,49-57. doi: 10.4236/jmf.2015.51005

References