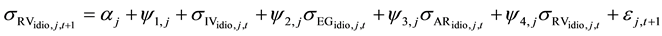Received 21 September 2014; revised 26 October 2014; accepted 9 November 2014

ABSTRACT

This paper investigates the role of volatility risk on stock return predictability. Using 596 stock options traded at the American Stock Exchange and the Chicago Board Options Exchange (CBOE) for the period from January 2001 to December 2010, it examines the relation between different idiosyncratic volatility measures and expected stock returns for a period that involves both the dotcom bubble and the recent financial crisis. First it is showed that implied idiosyncratic volatility is the best stock return predictor among the different volatility measures used. Second, cross-sec- tion firm-specific characteristics are important on stock returns forecast. Third, we provide evidence that higher short selling constraints impact negatively stock returns having liquidity the opposite effect.

Keywords:

Options, Risk Premium, Stock, Volatility

1. Introduction

Volatility is recognized to be central in asset pricing. An accurate forecast of future volatility delivers important information to market participants and, consequently, options can be essentially bet on volatility. Financial market volatility is not only important to option pricing but also a vital input for investment and financial market regulation. The volatile market environment and depressed expected returns of the past several years have increased the use of volatility strategies. No investor wants to be exposed to unnecessary risks that are not compensated by a return premium. There is an extensive literature on volatility prediction and broadly the best forecast of future volatility is the market’s prediction imbedded in implied volatility. Volatility is not merely a measure for the level of uncertainty prevailing in financial markets. In particular, investors are looking to diversify their portfolio strategy in recent years, becoming volatility a new asset class. Due to its complexity, a wide range of investment opportunities is offered. Moreover, investment strategies for institutional investors have been developed by making volatility as an asset class accessible in the form of structured products and certificates for retail investors.

[1] provides an extended literature review comparing volatility forecasting performance of two main approaches; historical volatility models and volatility implied from options. [2] - [4] among others, examine the predicting power of implied volatility finding that implied volatility is a bias predictor of future realized volatility. Other authors analyze whether other volatility forecast models such as GARCH, EGARCH and autoregressive model in 2^nd order are better predictors than implied volatility obtained by inverting the Black and Scholes model.

Although the time-series relation between the expected returns and market volatility has been considerably addressed in the literature ( [5] and [6] , among others) the question of how the cross-section of expected stock returns are affected by aggregate volatility has gathered less attention. [2] finds that low average returns are due to stocks with high idiosyncratic volatility. A significant strand of academic literature documented that cross- sectional effects such as liquidity risk, momentum, size and value factors could be controlled by cross-section of stock returns [7] - [9] . In fact these cross-sectional risk factors are not controlled by option pricing studies.

Another strand of literature ( [11] - [13] , among others) examines and finds cross-section association between idiosyncratic risk and stock returns. [10] explores the stock returns prediction by the information content of implied volatility stating that higher future returns tend to be associated with higher levels of volatility.

In this paper, we examine the role of volatility risk in stock returns predictability for 596 stock options traded at the American Stock Exchange and the Chicago Board Options Exchange (CBOE) for the period from January 2001 to December 2010.

This study aims to contribute to the existing literature on volatility measures, volatility risk and stock return predictability in a number of ways. First, to our knowledge, it is the first research analyzing the effect of different idiosyncratic volatility measures for a period that involves both the dotcom bubble and the recent financial crisis. This will shed light on the relation between idiosyncratic volatility and stock prices in periods when S&P500 dropped at least 20 percent. Second, the empirical findings will disclose more information on the accuracy of different volatility measures. Third, this research will extend the work of [2] by including and analyzing firm-specific characteristics. Fourth, we control for possible short-sale constraints and liquidity issues effect on stock returns.

The results can be summarized as follows. First, we find strong statistically significant evidence of idiosyncratic volatility on stock returns predictability. Second, the results show that implied idiosyncratic volatility is the best predictor among the different volatility measures used. There is clear evidence of a return premium for carrying idiosyncratic volatility risk. Third, we provide evidence of cross-section firm-specific characteristics on stock returns. Finally, we confirm that higher short selling constraints impact negatively stock returns having liquidity the opposite effect.

The rest of the paper is organized as follows¹. The next section presents the data sources and discusses sample selection and methodology implemented. In Section 3 we test the different volatility forecast models and the predictive power of idiosyncratic volatility on future stock returns and Section 4 concludes the study.

2. Data and Methodology

2.1. Sample

Our sample represents the US equity option market by comprising the stock options traded at the American Stock Exchange and the Chicago Board Options Exchange (CBOE) for the period from January 2001 to December 2010. The data to undertake the research was collected from different sources. 1) The daily implied volatility for each individual company and the option open interest were collected from Tick Data and Option Metrics; 2) Stock returns, share prices, and the number of shares outstanding are from Tick Data and CRSP and equity book value are from Tick Data and Compustat; 3) daily returns for the the Carhart (1997) momentum factor (UMD) and three Fama and French (1993) factors (MKT, SMB, HML) were collected from Kenneth French’s website.

From CRSP the full data comprises 2596 Tickers (or unique firms) for the period January 2001 to December 2010. The following sample selection criteria are imposed: 1) Full information (daily basis) for trade options, 2) Daily stock returns for at least the five previous years². In order to confirm whether our sample represents the US market as a whole, the sample average daily return was computed and the correlation between this average and the market return was calculated. The result shows a 90% of correlation among the market returns proxied by S&P500 and our sample meaning that the data can represent the US market as a whole³.

Table 1 reports the initial number of firms per industry available in CRSP for the period January 2001 and December 2010 and the number of sampling firms after the previous presented selection criteria.

Overall there are 596 unique firms in our sample which represents 22.9 percent of full data available in CRSP. There is no evidence of a single industry to be more represented in the sample. In fact, the percentage of unique firms per industry presented in the sample is very similar with values between 21.7 and 23.9 percent for Utilities and Consumer Goods, respectively.

2.2. Methodology

2.2.1. Beta, Implied and Realized Idiosyncratic Volatilities

1) Beta calculation

The firm’s beta for each of the unique firms selected is calculated in a 60 months rolling basis. The firm’s beta is estimated by the regression of stock returns 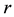on market returns Mret for each month with the use of the previous 60 months:

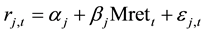(1)

where, Mret is the S&P500 value-weighted monthly returns collected from CRSP, 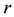is the stock monthly returns, 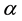represents the constant term and 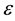is the error term. Furthermore, the beta calculation robustness is verified by applying the [9] three factor model and a beta portfolio computed following [14] creating equal-weighted returns in a rolling monthly estimation for portfolios of depending on firm’s number and size betas. Then, the regression of these portfolios returns are regressed on the S&P500 value-weighted monthly returns with one-month lag to determine portfolio betas for the individual firms based on their beta level and size.

2) Implied idiosyncratic volatility calculation

Data is gathered as refereed from Option Metrics employing European and American models upon appropriated. The standardized implied volatility is estimated by using the option nearest to 30 days to maturity and at-the-money for both puts and calls to deduct the measurement error related to the conversion to attain implied volatilities from option prices⁴.

Analogous to [16] for the computation of the implied volatility in its idiosyncratic part the market implied volatility is demonstrated to be a market volatility function:

(2)

where, 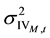is the VIX implied market variance for day, is the total implied variance at time for firm, 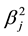is the squared market beta from Equation (1) and is the implied variance in the idiosyn-

cratic part at time for firm. Thus, the measurement of implied idiosyncratic volatility is the square root of the implied variance of the idiosyncratic part. In theory, this value would not be equal to zero or negative but it is possible empirically to occur⁵.

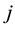
3) Realized idiosyncratic volatility calculation

The annualized realized volatility is calculated for each month and firm as the annualized standard deviation of daily returns. The realized idiosyncratic volatility part is calculated through Equation (1) using daily observations. The realized idiosyncratic risk is calculated from daily residuals standard deviation for each month and firm, such that:

(3)

where, is the number of trading days in each month, is the residual for firm on day for month and is the mean residual in month over the days for firm. The is measured in annual basis.

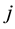
2.2.2. GARCH and AR (2)

The advantage of the EGARCH versus the GARCH model is the no requirement to restrict the parameters to assure a non-negative variance. This function is formed as:

(4)

where the monthly returns are calculated following the Fama and French (1993) 3-factor model in Equation (4)

and the conditional variance for firm is a function of the past residual variances and stock returns.

(5)

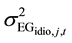
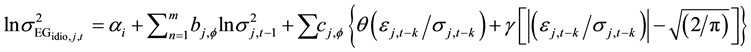
where, and are estimated coefficients and the number of firms with options in the sample. Equations (4) and (5) are computed at least for 60 monthly returns for each stock. The idiosyncratic volatility is calculated as the square root of the conditional variance.

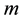
For the autoregressive model in 2^nd order, AR (2) for the idiosyncratic volatility estimation we follow [17] . Applying Equation (4) to calculate the square residual, the idiosyncratic variance for firm is calculated as:

(6)

The idiosyncratic volatility is defined as the square root of the idiosyncratic variance.

2.2.3. Short-Sale and Liquidity

Additionally for possible short-sale constraints or liquidity issues are controlled. Particularly, highly liquid stocks are less likely to get market frictions and consequently this has an important impact in traded options. The liquidity measure open-interest is calculated as one plus the option open-interest logarithm, where open-interest is compiled for each firm across the all options. For the measure of short-sale constraint we follow [18] as:

(7)

where is the theoretical price computed from the call-put relation including the put of last exercise premium⁶ and is the current stock price. The ORW Ratio should exceed zero if a short-sale constraint exists.

In summary the control for possible short-sale constraints or liquidity issues are performed to test the hypothesis whether short-sale constraints and/or higher liquidity impacts prices differently in response to volatility than those from more restricted companies.

2.2.4. Realized Volatility Prediction

1) Implied volatility

How well does implied volatility (IV) predict future realized volatility (RV) is measured at both individual (firm) and market levels. The following regressions are performed:

(8)

and,

(9)

where, is the annualized realized monthly volatility in month for the S&P500 index, is the

VIX index in month, is the constant term, and are estimated coefficients and is the error term. The regression specification at individual/firm level is shown in Equation (9). The equation is performed to each firm independently, whilst the mean and median coefficients are presented as well respective significance.

, represents the annualized realized monthly volatility in month for each unique firm, is the

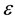
implied volatility for each firm in month, is the constant term, and are estimated coefficients and is the error term.

2) Implied idiosyncratic volatility

Additionally this paper tests the power of implied idiosyncratic volatility, and EGARCH and AR (2) volatility forecast models to predict realized idiosyncratic volatility. The following regression is estimated:

(10)

where, represents the realized idiosyncratic volatility in month for firm, is the implied variance in its idiosyncratic part at month for firm, , is conditional variance for firm in month is, , is the idiosyncratic volatility estimation following [17] autoregressive model in 2^nd order, AR (2), is the constant term,’s estimated coefficients and is the error term.

2.2.5. Predictive Regressions

1) Fama-Macbeth (1973)

The final step is to examine the relation between idiosyncratic risk and firm future returns. We extend the study of [2] by including firm specific characteristics in our analysis. As a result we assess in a monthly basis and at firm level the relation between idiosyncratic volatility and future stock returns, applying firm-specific controls and following [19] procedure. The following regression is estimated:

(11)

where, represents the stock return for firm for firm in month, , is the realized idiosyncratic volatility in month for firm, , is the logarithm of market value of equity (calculated by multiplying the company’s current stock price by its number of outstanding shares), , is the logarithm of the book-to-market ratio, and, represents the stock return for firm one and three years

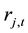
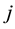
before the current month, , is firm equity Beta, is the constant term,’s estimated coefficients and is the error term.

Additionally, the previous equation is modified by including the idiosyncratic volatility forecasts (implied volatility, EGARCH and AR (2)), short-sale constraints and liquidity issues. The regression will proceed as follow:

(12)

where, represents the stock return for firm for firm in month, , is the realized idiosyncratic volatility in month for firm, , is the logarithm of market value of equity (calculated by multiplying the company’s current stock price by its number of outstanding shares), , is the logarithm of the book-to-market ratio, and, represents the stock return for firm one and three years before the current month, , is firm equity beta, , is the implied variance in its idiosyncratic part at month for firm, , is conditional variance for firm in month is, , is the idiosyncratic volatility estimation following [17] autoregressive model in 2^nd order, AR (2), , is the

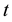
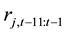
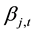
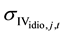
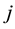
ORW ratio following [18] , , is the liquidity measure open-interest, is the constant term,’s estimated coefficients and is the error term.

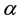
2.3. Data Sources and Description

Table 2 below summarizes the data sources and equations description for each of the research steps detailed previously.

3. Empirical Results

We first start by presenting a brief overview of summary statistics for the variables used in this study followed by preliminary tests whether lagged historical/implied volatilities or EGARCH and AR (2) models better explain realized volatility. We finish with the Predictive Regressions analysis. The sample represents the US equity option market by comprising the stock options traded at the American Stock Exchange and the Chicago Board Options Exchange (CBOE) for the period from January 2001 to December 2010. Our sample comprises 596 unique firms. To ensure that the sample represents the US market as a whole, the correlation between the average daily return per stock and the market return (proxied by S&P500) was calculated. The correlation between the average sample returns and market return is above 90 percent showing that our sample represents appropriately the US market as a whole.

3.1. Descriptive Statistics

Table 3 reports per year summary statistics for the 596 unique firms analysed. We can highlight the increased

volatility in 2001-2002 (dotcom bubble)⁷ and 2008-2009 (recent financial crisis). Additionally the implied volatility annual standard deviation increases in the two cited periods, a clear evidence of the no homogeneous increase in volatility among the different stocks in our sample, supporting that differences in firms and industry sectors do exist.

Table 4 presents the same analysis regarding the historical volatility. In fact historical volatility is higher on 2001-2002 and 2008-2009 periods. We can also detect a higher average implied volatility comparing with historical volatility in our sample possible indicating that options are overvalued⁸.

In Figure 1 and Figure 2 it is presented the average monthly implied and historical volatilities per industry.

The volatility increase in the years 2001-2002 and 2008-2009 is observed independently of the industry analysed. However, there is a clear evidence of higher volatility (both implied and historical) of technology firms in the period 2001-2002 and Financials in 2008-2009.

3.2. Preliminary Analysis

To examine the predictive power of realized and implied volatility, we test the forecast accuracy of both by performing time series regression at firm level of historical volatility lagged one day and with one day lag of implied volatility.

where, RV is the stacked vector of the dependent variable representing the realized volatility for each of the 596 stocks for the period January 2001 to December 2010, is the constant term, IV and RV are vectors with the implied and realized volatility one month before for each of the 506 stocks, respectively, and is the error term.

Table 5 shows a summary of the results for the 596 unique regressions. Overall the implied volatility coefficient is significance at 1 percent level for 423 of the 596 regressions (average coefficient 0.558)⁹, whereas the historical volatility is significant in only 346 cases and with a lower coefficient.

In Table 6 we extend the analysis and test the forecast accuracy for the alternative idiosyncratic volatility measures used in this paper. We compare the historical, implied and the EGARCH and AR (2) volatility forecast models, running time series regressions at firm level for the period January 2001 to December 2010. We apply Equation (10), where:

From the results presented in Table 6, implied and historical volatility are the most accurate methods in predicting and forecasting next period (month) realized volatility. In fact, for 68 (66) percent of the cases implied (historical) volatility is statistical significant at 10 percent level whereas for EGARCH and AR (2) just in 19 and 45 percent, respectively. Additionally, in around 50 percent of the firm-level regressions the historical and implied volatilities are statistical significant at 1 percent level. We will implement later additional tests of forecasting accuracy when the stock returns predictive regressions applying [19] were executed.

We next present a summary of variable statistics in Table 7. On average, for the 596 unique firms and for the period January 2001 to December 2010, the annual implied volatility accounts for 50.6 percent. This relatively high value is due to the fact that the dotcom bubble and the recent financial crisis are included in the sample period, which is one of aims of this paper. If one just considers the idiosyncratic risk the average implied and realized volatility values drop between 20 to 30 percent. Moreover, the EGARCH and AR (2) volatility forecast models present a higher idiosyncratic volatility than the historical and implied volatilities approach. According to [3] findings, divergences in realized and implied market volatilities might be a straight cause from a volatility risk premium which meaningfully affects the underlying option value. At firm level this volatility premium possible induces option prices in the same way. The comparison between median and mean values the idiosyncratic part of realized entire volatility is estimated to be 80.5 percent. This value is slight lower than the 85.7 percent reported by [20] . The median and mean implied idiosyncratic volatility is analogous to the realized idiosyncratic volatility and the idiosyncratic volatility is around 75 percent on entire implied volatility. The realized entire volatility is better explained by the realized idiosyncratic volatility than the implied total volatility described by implied idiosyncratic volatility. Furthermore, the idiosyncratic volatility would be a strong predictive component of realized volatility if most of the implied volatility is idiosyncratic at firm-level.

The book-to-market ratio exhibit an average value of 0.53, the equity beta average is 1.21 but the median value is very close to 1. Additionally, the total number of options contracts that are not closed or delivered on a particular day is on average 11.21 and there is a slight evidence of short selling constraints given that the average ORW Ratio exceed zero.

As the last step, the correlation matrix is presented in Table 8 for the independent variables used in the [19] predictive regressions. One can highlight the following correlation (univariate relationships) among the independent variables: 1) larger firms have lower implied and realized idiosyncratic volatilities and lower book to market ratios. Additionally they have higher betas and increased short selling constraints; 2) Larger returns are associated to firms with higher betas and lower idiosyncratic volatilities; 3) Higher equity beta firms are linked with lower idiosyncratic volatilities and higher open-interest; and 4) firms with more evidence of short selling constraints have on average lower number of options contracts.

3.3. Predictive Regressions

3.3.1. Future Realized Volatility

We first start by examining whether implied and realized volatilities from a specific month explain the realized volatility one month ahead. We test this relationship for both market (proxied by VIX and S&P500) and at firm level. Equations (8) and (9) are applied, where:

and,

Table 9 present our results. We find that implied volatility does contain information in forecasting realized volatility being the relation stable for both market and firm-level estimates. The results are aligned with [21] which analysed the relationship between implied and realized volatility by using daily S&P500 index option prices over the period between January 1995 and December. However it was found a lower coefficient estimate

^***, ^**, ^*Statistical significant for 1, 5, and 10 percent levels.

at the market level but with higher significance and almost double R-squared. Moreover, at market level results support [22] findings that implied volatility is a proficient forecaster of future realized volatility even in the presence of past realized volatility. The implied volatility coefficient is divergent of one resulting that implied volatility is an upward biased forecaster of future realized volatility which highlight the existence of a robust volatility risk premium.

In panel B (firm-level estimates) the results at firm level are reported. The evidence reported is analogous to the outcomes at market level. Firm implied volatility is still a statistical significant forecaster (at 1 percent level) of future realized volatility when past volatility is included as well. However, our results diverge from [23] and [16] which claims that implied volatility is an unbiased and proficient predictor of future realized volatility. In our study we find evidence that implied volatility as an upward biased forecaster of future volatility at both market and firm-levels.

Next it is regressed the idiosyncratic volatility in its different formulations with the realized volatility one month ahead, applying Equation (10) as below:

Table 10 reports the results. Model 1 shows that future realized idiosyncratic volatility is positively and statistically significant (at 1 percent level) related with both historical realized and implied idiosyncratic volatility. We could not find statistical significant when EGARCH forecast model is used (model 2) but some evidence is reported for AR (2). In both cases the historical realized idiosyncratic volatility increases, a clear evidence of a statistical significant relation between realized and implied idiosyncratic volatilities as reported in the correlation matrix. In model 4 we present the whole measures of idiosyncratic volatility where it is clear the strong predicting power of implied idiosyncratic volatility on future realized idiosyncratic volatility. Though, as reported in Table 9, implied idiosyncratic volatility is as well an upward biased forecaster of future realized idiosyncratic volatility.

3.3.2. Realized Returns

In a following step in Table 11 the predicting power of realized idiosyncratic volatility, other firm-specific characteristics and previous firm returns are analysed. This is done for both full data (2596 firms) and the selected sample (596 unique firms) by applying monthly cross-sectional regressions using [19] .

As previously referred the variables SIZE and B/M ratio are calculated at the end of each month and the return variables are lagged 1, 11 and 36 months. Results are not statistically different between full data and sample. Indeed, we cannot find evidence of realized idiosyncratic volatility on firms realized returns, size has a negative effect on stock returns whereas B/M ratio has a positive effect. Our results are aligning with the ones from [2] and [24] in terms of the relation among future stock returns and idiosyncratic realized volatility. Additionally we find a negative statistical significant effect of last month stock return on the next month return and no clear evidence of last year and three years ago stock returns was reported. Finally, the equity beta is not statistically significant at all for both the full data and the sample used in this paper. Larger firms tend systematically to offer lower returns and firms with high B/M ratios deliver higher returns to their investors.

As the last step Equation (12) with is run for different combinations of independent variables (models 1 to 10)

^***, ^**, ^*Statistical significant for 1, 5, and 10 percent levels.

^***, ^**, ^*Statistical significant for 1, 5, and 10 percent levels.

by applying monthly cross-sectional regressions using [19] . Results are presented in Table 12. They show a strong and statistically significant effect (1 percent level) of implied idiosyncratic volatility on future stock returns. In fact a one percent increase in the implied idiosyncratic volatility increase future returns between 0.03 and 0.042 percent (depending on the model specification). Therefore, there is a premium for carrying implied idiosyncratic volatility and higher returns are partially due to idiosyncratic volatility risk. Inversely realized idiosyncratic volatility is meaningless to all model specifications. Additionally, we find evidence for the EGARCH and AR (2) volatility forecast models as a stock return predictor, however, with lower effect and significance than implied idiosyncratic volatility. Moreover the equity betas have a positive coefficient but only significant to fewer model specifications. The short-sales constraint variable has a statistically significant coefficient revealing that when the constraint is higher the return is per se lower. In relation to the open-interest variable as a proxy for liquidity we find a positive statistically significant effect of stock returns.

4. Conclusions

This paper investigates, the role of volatility risk on stock returns predictability for 596 stock options traded at the American Stock Exchange and the Chicago Board Options Exchange (CBOE) for the period from January 2001 to December 2010. Using a time period that incorporates both the dotcom bubble and the recent financial crisis we shed light on the relation between idiosyncratic volatility and stock prices in periods when S&P500 dropped at least 20 percent.

The findings confirm the impact of idiosyncratic volatility on stock returns predictability; the best predictor among the different volatility measures used is the implied idiosyncratic volatility and there is a clear evidence of a return premium for carrying idiosyncratic volatility risk. Indeed, a one-percent increase in the implied idiosyncratic volatility increases future returns between 0.03 and 0.042 percent.

We also discovered that cross-section firm-specific characteristics were important for stock returns prediction and confirmed the importance of short-selling constraints and liquidity issues. Evidence is provided that higher short selling constraints impact negatively stock returns having liquidity the opposite effect.

Overall, we claim that this research provides a significant contribution to the existing evidence on volatility measures, volatility risk and stock return predictability. To our knowledge it is the first time that a period that involves both the dotcom bubble and the recent financial crisis is analyzed.

The volatile market environment and depressed expected returns of the past several years have increased the use of volatility strategies. Now that volatility has emerged not only as a concept but also as an investment in its own right, this study brings light to the accuracy of different forecast models in idiosyncratic volatility calculation and its effect on future stock returns.

This research was conducted by examining the effect of idiosyncratic volatility on stock returns predictability and could be continued further by examining sub-periods of bear and bull markets and industry specific effects on volatility risk and stock returns predictability.

References

NOTES

¹Extended version of this paper is available online.

²This condition is essential for the calculation of idiosyncratic realized, implied volatility and the firm’s beta.

³Results are available upon request.

⁴For details see [15] .

⁵The small values are set equal to zero and there are non-positive values.

⁶Refer to [18] .

⁷S&P500 index drops by 13.04 and 23.37 percent in 2001 and 2002, respectively.

⁸When implied volatility is greater than historical volatility, options are thought to be overvalued, and when implied volatility is less than historical volatility, options are considered to be undervalued.

⁹In parenthesis it is shown the percentage of firms related to full sample.