Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:55769,12 pages
10.4236/jmf.2015.52012
On the Study of Reduced-Form Approach and Hybrid Model for the Valuation of Credit Risk
Olaronke Helen Edogbanya1, Sunday Emmanuel Fadugba2
1Department of Mathematics, Federal University, Lokoja, Nigeria
2Department of Mathematical Sciences, Ekiti State University, Ado Ekiti, Nigeria
Email: helyna4christ@yahoo.com, emmasfad2006@yahoo.com,
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2014; accepted 16 April 2015; published 17 April 2015
ABSTRACT
This paper presents the study of reduced-form approach and hybrid model for the valuation of credit risk. Credit risk arises whenever a borrower is expecting to use future cash flows to pay a current debt. It is closely tied to the potential return of investment, the most notable being that the yields on bonds correlate strongly to their perceived credit risk. Credit risk embedded in a financial transaction, is the risk that at least one of the parties involved in the transaction will suffer a financial loss due to decline in creditworthiness of the counter-party to the transaction or perhaps of some third party. Reduced-form approach is known as intensity-based approach. This is purely probabilistic in nature and technically speaking it has a lot in common with the reliability theory. Here the value of firm is not modeled but specifically the default risk is related either by a deterministic default intensity function or more general by stochastic intensity. Hybrid model combines the structural and intensity-based approaches. While avoiding their difficulties, it picks the best features of both approaches, the economic and intuitive appeal of the structural approach and the tractability and empirical fit of the intensity-based approach.
Keywords:
Credit Risk, Hybrid Model, Reduced-Form Approach, Risk-Neutral Valuation Formula

1. Introduction
As stock markets have become more sophisticated, so have their products. The simple buy or sell trades of the early markets have been replaced by more complex financial options and derivatives. These contracts can give investors various opportunities to tailor their deals to their investment needs.
The main emphasis in the intensity-based approach is put on the modelling of the random time of default, as well as evaluating condition expectations under a risk-neutral probability of functionals of the default time and corresponding cash follows. Typically, the random default time is defined as the jump time of some one-jump process.
In recent years, we see a spectacular growth in trading, especially in derivative instruments. There is also an increasing complexity of products in the financial markets with the growing complexity and trading size of financial markets; mathematical models have come to play an increasingly important role in financial decision making, especially in the context of pricing and hedging of derivative instruments. Models have become indispensable tools in the development of new financial products and the management of their risks.
Credit risk is defined as the changes in the credit quality of a borrower. This is called the spread risk. If a borrower has a lower quality ranking we expect that he will be less able to pay off his running-up debt. Therefore credit risk is characterized by two risks: default risk and spread risk. The importance of valuation and hedging models in derivatives markets cannot be over-emphasized. The financial risk can therefore be categorized into four (4) types namely: Market risk, Liquidity risk, Operational risk and Credit risk.
The first category of credit risk models are the ones based on the original framework developed by Merton [1] . They derived an explicit formula for risky bonds which can be used both to estimate the probability of default of a firm and to estimate the yield differential between a risk bond and a default-free bond. In addition to Merton [1] , first generation structure-firm models include Black and Cox [2] . They try to refine the original Merton framework by removing one or more of the unrealistic assumptions. Black and Cox [2] introduced the possibility of more complex capital structure with subordinated debts, using the principles of option pricing Black and Scholes [3] . In such a framework, the default process of a company is driven by the value of the company’s assets and the risk of a firm’s default is therefore explicitly linked to the variability of the firm’s asset value. The basic intuition behind the Merton model is that, default occurs when the value of a firm’s assets (the market value of the firm) is lower than that of its liabilities.
Reduced-form models somewhat differ from each other by the manner in which the recovery rate is parameterized. For example, Jarrow and Turnbull [4] assumed that, at default, a bond would have a market value equal to an exogenous specified fraction of an otherwise equivalent default-free bond. Duffie and Lando [5] would have a market value equal to an exogenously specified fraction of an otherwise equivalent default-free bond. Duffie and Singleton [6] followed with a model that when market value at default (recovery rate) is exogenously specified, allows for closed-form solutions for term-structure of credit spreads. Hybrid model is the combination of ideas from both the structural and intensity-based approaches; this is by postulating that the hazard rate of default (intensity) event is directly linked to the current value of the firm’s assets (or the firm’s equity).
For mathematical background, valuation of credit risk, some numerical method for options valuation and stochastic analysis based on the Ito integral, see [7] -[20] , just to mention a few. This paper is structured as follows. Section 2 presents the reduced-form model. Section 3 discusses hazard processes. Section 4 presents hybrid model for the valuation of credit risk. Section 5 concludes the paper. In this paper we shall consider reduced- form approach and hybrid model for the valuation of credit risk.
2. Reduced-Form Model
In this approach, the value of the firm’s assets and its capital structure are not model at all, and the credit events are specified in terms of some exogenously specified jump process (as a rule, the recovery rates at default are also given exogenously). We can distinguish between the reduced-form models that are only concerned with the modelling of default time, and that are henceforth referred to as the intensity-based models, and the reduced form models with migrations between credit rating classes called the credit migration models.
The main emphasis in the intensity-based approach is put on the modelling of the random time of default, as well as evaluating condition expectations under a risk-neutral probability of functionals of the default time and corresponding cash follows. Typically, the random default time is defined as the jump time of some one-jump process. As well shall see, a pivotal role in evaluating respective conditional expectations is played by the default intensity process.
Modelling of the intensity process which is also known as the hazard rate process, is the starting point in the intensity approach.
2.1. Hazard Function
Before going deeper in the analysis of the reduced-form approach, we shall first examine a related technical
question. Suppose we want to evaluate a conditional expectation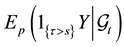 , where τ is a stopping time on
, where τ is a stopping time on
a probability space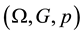 , with respect to some filtration
, with respect to some filtration 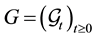 and Y is an integrable,
and Y is an integrable, 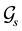 -measura- ble random variable for some
-measura- ble random variable for some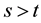 .
.
In financial applications, it is quite natural and convenient to model the filtration G as G = FVH, where h is the filtration that carries full information about default events (that is, events such as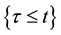 ), whereas the reference filtration F carries information about other relevant financial and economic processes, but, typically, it does not carry full information about default event. The first question we address is how to compute the expectation
), whereas the reference filtration F carries information about other relevant financial and economic processes, but, typically, it does not carry full information about default event. The first question we address is how to compute the expectation
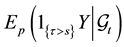 (2.1)
(2.1)
Using the intensity of τ with respect to F.
2.1.1. Hazard Function of a Random Time
We study the case where the reference filtration F is trivial, so that it does not carry any information whatsoever. Consequently, we have that G = h. Arguably, this is the simplest possible used in practical financial applications, as it leads to relatively easy calibration of the model.
We start by recalling the notion of a hazard function of a random time. Let τ be a finite, non-negative random time.
Let τ be a finite, non-negative, variable on a probability space , referred to as the random time. We assume that
, referred to as the random time. We assume that 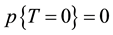 and τ is unbounded;
and τ is unbounded;
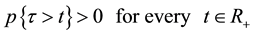 (2.2)
(2.2)
The right continuous cumulative distribution function F of τ satisfies
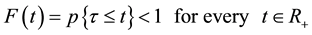 (2.3)
(2.3)
We also assume that 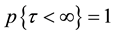 so that τ is a Markov time.
so that τ is a Markov time.
We introduce the right-continuous jump process 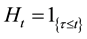 and we write
and we write 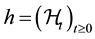 to denote the (right continuous and p-completed) filtration generated by the process H. Of course, τ is an h-stopping time.
to denote the (right continuous and p-completed) filtration generated by the process H. Of course, τ is an h-stopping time.
We shall assume throughout that all random variables and processes that are used in what follows satisfy suitable integrability conditions. We begin with the following simple and important result.
Lemma 1
For any 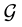 -measurable (integrable) random variable Y we have
-measurable (integrable) random variable Y we have
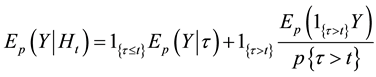 (2.4)
(2.4)
For any 

that is, 


The hazard function is introduced through the following definition.
Definition 1: The increasing right-continuous function 

is called the hazard function of a random time τ.
If the distribution function F is an absolutely continuous function, i.e., if we have
for some function
where we set


The function 
Definition 2: The dividend process D of a defaultable contingent claim
D is a process of finite variation and
Note that if default occurs at some date t, the promised dividend


Remark: In principle, the promised payoff X could be incorporated into the promised dividends process C. However, this would inconvenient, since in practice the recovery rules concerning the promised dividend C as the promised claim X are different, in general. For instance, in the case of a defaultable coupon bond, it is frequently postulated that in case of default the future coupons are lost, but a strictly positive fraction of the face value is usually received by the bondholder.
Corollary 2: For any 

Corollary 3: Let Y be 



If, in addition, the random time τ admits the hazard rate function γ then we have

In particular, for any 

and

Lemma 4: The process L, given by the formula
is an h-martingale.
2.1.2. Martingales Associated with Continuous Hazard Function
The h-adapted process of finite variation L given by last formula is an h-martingale (for Γ continuous or a discontinuous function).
We examine further important examples of martingales associated with the hazard function, with the assumption that the hazard function Γ of a random time τ is continuous. Also we assume that the cumulative distribution function F is absolutely continuous function, so that the random time τ admits the intensity function γ, our goal is to establish a martingale characterization of γ.
More specifically, we shall check directly that the process
follows and h-martingale. To this end,
On the other hand, if we denote
Let us set

This shows that the process 
2.1.3. Martingale Hazard Function
Lemma 5: Assume that F (and this also the Hazard function Γ) is continuous function. Then the process

is h-martingale.
In view of the martingale in Lemma 5, the following definition is natural.
Definition 3: A function 
Remarks: Since the bounded, increasing process H is constant after time τ its compensation is constant after τ as well. This explains why the function 

It happens that the martingale hazard function can be found explicitly. In fact, we have the following.
Proposition 6: The unique martingale hazard function of τ with respect to the filtration h is the right-conti- nuous increasing function 


Observe that the martingale hazard function 

We conclude that the martingale hazard function 
In general, we have

where

2.2. Default Table Bonds: Deterministic Intensity
In order to value a defaultable claim, we need, of course, to specify the unit in which we would like to express all prices. Formally, this is done through a choice of discount factor (a numeraire). For the sake of simplicity, we shall take the savings account

as the numraire, where r is the short term interest rate process.
We also postulate that some probability measure 
In accordance with our assumption that the reference filtration is trivial, we also assume that:
・ the default time τ admits the 
・ the short-term interest rate 
In view of the latter assumption, the price at time t of a unit default-free zero-coupon bond of maturity T equals

In the market practice, the interest rate (more precisely, the yield curve) can be derived from the market price of the zero-coupon bond. In a similar way the hazard rate can be deduced from the prices of the corporate zero- coupon bonds, or from the market values of other actively traded credit derivatives.
In view of our earlier notation for defaultable claims adopted, for the corporate unit discount bond we have 


2.3. Zero Recovery
Consider first a corporate zero-coupon bond with unit face value, the maturity date T, and zero recovery at default (that is, 


The price 

where 

2.3.1. Fractional Recovery of Par Value (FRPV)
According to this convention, we have 


Using Corollary 3, we check that the pre-default value 

where 





2.3.2. Fractional Recovery of Treasury Value (FRTV)
Assume now that 


Let us denote by 
or equivalently,

In the case of full recovery, that is, for

Remarks. Similar representations can be derived also in the case when the reference filtration F is not trivial, and under the assumption that market risk and credit risk are independent that is:
・ the default time admits the F-intensity process γ,
・ the interest rate process r is independent of the filtration F.
3. Hazard Processes
In the previous section, it was assumed that the reference filtration F carries no information. However, for practical purposes it is important to study the situation where the reference filtration is not trivial. This section presents some results to this effect.
We assume that a martingale measure Q is given, and examine the valuation of defaultable contingent claims under this probability measure. Note that the defaultable market is incomplete if there are no defaultable assets traded on the market that are sensitive to the same default risk as the defaultable contingent claim we wish to price. Thus, the martingale measure may not be unique.
3.1. Hazard Process of a Random Time
Let 



We start by extending some definitions and results to the present framework. We denote




Definition 4: The F-hazard process Γ of a random time τ is defined through the equality

Notice that the existence of Γ implies that τ is not an F-stopping time. If the event 





If the hazard process is absolutely continuous, so that


3.2. Terminal Payoff
The valuation of the terminal payoff 
The question is how to compute 

Lemma 7: For any 


If, in addition, Y is 

Assume that Y is 



The latter property can be extended to stochastic process: for any G-predictable process X there exists an F- predictable process 

is valid for every

3.3. Recovery Process
The following extension of Corollary 3 appears to be useful in the valuation of the recovery payoff 
Lemma 8: Assume that the hazard process Γ is a continuous, increasing process, and let Z be a bonded, F-predictable process. Then for any 

3.4. Promised Dividends
To value the promised dividends (that are paid prior to τ, it is convenient to make use of the following result.
Lemma 9: Assume that the hazard process Γ is continuous. Let C be a bounded, F-predictable process of finite variation. Then for event

3.5. Valuation of Defaultable Claims
We assume that τ is given on a filtered probability spaces




The probability 

The ex-dividend price 

Definition 5: For any date


we always set





Proposition 10: The value process of a defaultable claim 
If the hazard process Γ is an increasing, continuous process, then
Corollary 11: Assume that the F-hazard process Γ is a continuous, increasing process. Then the value process of a defaultable contingent claim 


3.6. Defaultable Bonds: Stochastic Intensity
Consider a defaultable zero-coupon bond with the par (face) value L and maturity date T. First, we re-examine the following recovery schemes: the fractional recovery of par value and the fractional recovery of Treasury value. Subsequently, we shall deal with the fractional recovery of pre-default value, but in this section using the stochastic intensity instead of the deterministic intensity used earlier. We assume that τ has the E-intensity γ.
3.7. Functional Recovery of Par Value
Under this scheme, a fixed fraction of the face value of the bond is paid to the bondholders at the time of default. Formally, we deal here with a defaultable claim





If τ admits the F-intensity γ, the pre-default value of the bond equals

Remarks. The above setup is a special case of the fractional recovery of par value scheme with a general F- predictable recovery process




3.8. Fractional Recovery of Treasury Value
Here, in the case of default, the fixed fraction of the face value is paid to bondholders at maturity date T. A corporate zero-coupon bond is now represented by a defaultable claim 




The price of this claim oat time 

or equivalently,

The pre-default value 

Again, the last formula is special case of the general situation where 

3.9. Fractional Recovery of Pre-Default Value
Assume that 



where

3.10. Choice of a Recovery Scheme
A challenging practical problem is the calibration of statistical properties of both the recovery process δ and the intensity process γ. The empirical evidence strongly suggests that the amount recovered at default is best modelled by the recovery of par value scheme. However, we conclude that recovery concept that specifies the amount recovered as fraction of appropriately discounted par value, that is, the fractional recovery of treasury value, has broader empirical support.
4. Hybrid Model
This is basically combination of ideas from both the structural and intensity-based approaches, this is by postulating that the hazard rate of default (intensity) event is directly linked to the current value of the firm’s assets (or the firm’s equity). Reduced-form models with this specific feature are referred to as hybrid model. In this setup, the default time is still a totally inaccessible stopping time, but the likelihood of default may grow rapidly when the total value of the firm’s assets approaches some barrier. Madan and Unal [20] consider the discounted equity value (including reinvested dividends) process 
They postulate that the hazard rate of default equals 




Under the martingale measure 









We take a function

notice that the stochastic intensity 


The futures price 

In particular, the futures price 

More explicitly,
for some function
By virtue of Equation (4.1) and the Feynman-Kao theorem, the function r satisfies, under mild technical assumptions, the following pricing partial differential equation

subject to the terminal condition


where the parameter v satisfies 

For a fixed value of the parameter v, the function 

with the initial conditions 

serve to produce estimates of parameters of the hazard rate process, based on the observed market yields on defaultable bonds.
5. Conclusion
We have in our disposal two models for the valuation of credit risk named the reduced-form model and the hybrid model. It is worth noting that the cornerstone of credit risk and its modelling is based on the information one can perceive. This information can be complete (structural approach), partial (incomplete information model which is called hybrid model) or not available (reduced-form model). This perceived information defined the methodology that one can apply to model credit risk. Everything lies on whether information is available or not. And that is the very fundamental economic notion of credit risk. We conclude this paper by commenting on the advantages and disadvantages of the reduced-form model and the hybrid model for the valuation of credit risk.
5.1. Advantages of Reduced-Form Model
・ The level of the credit risk is reflected in a single quantity: the risk-neutral default intensity.
・ The random time of default is an unpredictable stopping time, and thus the default event comes as an almost total surprise.
・ The valuation of defaultable claims is rather straightforward. It resembles the valuation of default-free contingent claims in term structure models, through well understood techniques.
・ Credit spreads are much easier to quantify and manipulate than in structural models of credit risk. Consequently, the credit spreads are more realistic and risk premia are easier to handle.
・ The intensity of the random time of default plays the role of a models input.
・ Valuation result for corporate bonds and credit derivatives are relatively simple, even in the case of basket credit derivatives.
・ In practice, the intensity of default can be inferred from observed prices of bonds (the calibrated or implied default intensity).
5.2. Disadvantages of Reduced-Form Model
・ Value of the firm is not explicitly modelled.
・ Typically, current data regarding the level of the firm’s assets and the firm’s leverage are not taken into account.
・ Specific features related to safety covenants and debt’s seniority are not easy to handle.
・ All (important) issues related to the capital structure of a firm are beyond the scope of this approach.
・ Most practical approaches to portfolio’s credit risk are linked to the value-of-the-firm approach.
5.3. Advantages of Hybrid Model
・ This is basically combination of ideas from both the structural and intensity based approaches. While avoiding their difficulties, it picks the best features of both approaches: the economic and intuitive appeal of the structural approach and the tractability and empirical fit of the intensity-based approach.
・ Hybrid model is of great importance in credit risk valuation because of the existence of a bankruptcy process.
・ Dependent defaults are easy to handle through correlation of processes corresponding to different names.
5.4. Disadvantages of Hybrid Model
・ A stringent assumption that the total value of the firm’s assets can be easily observed. In practice, continuous-time observations of the value processes are not available. Thus the structural model with incomplete accounting data can be dealt with using the intensity-based methodology.
・ Most practical approaches to portfolio’s credit risk are linked to the value-of-the-firm approach.
References
- Merton, R.C. (1974) On the Pricing of Coporate Debt: The Risk Structure of Interest Rates. Journal of Finance, 29, 449-470.
- Black, F. and Cox, J.C. (1976) Valuing Corporate Securities: Some Effects of Bond Indenture Provisions. Journal of Finance, 31, 351-367. http://dx.doi.org/10.1111/j.1540-6261.1976.tb01891.x
- Black, F. and Scholes, M. (1973) The Pricing of Options and Coporate Liabilities. Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
- Jarrow, R.A. and Turnbull, S.M. (1995) Pricing Derivatives on Financial Securities Subject to Credit Risk. The Journal of Finance, 1, 53-85. http://dx.doi.org/10.1111/j.1540-6261.1995.tb05167.x
- Duffie, D. and Lando, D. (2001) The Term Structure of Credit Spreads with Incomplete According Information, Econometrica, 69, 633-664. http://dx.doi.org/10.1111/1468-0262.00208
- Duffie, D. and Singleton, K. (1999) Credit Risk Pricing and Risk Management for Financial Institutions. Princeton University Press, Princeton.
- Ammann, M. (1999) Pricing Derivative Credit Risk. Springer-Verlag, New York.
- Crouly, M., Galev, D. and Mark, R. (1998) Credit Risk Revisited, Risk-Credit Risk Supplement. 40-44.
- Davis, M. and Lo, V. (2001) Infectious Default. Quantitative Finance, 1, 382-386. http://dx.doi.org/10.1080/713665832
- Dellacherie, C. (1972) Capacities et Processus Stochastique. Springer-Verlag, Brelin, Heidelberg, New York.
- Elliott, R.J. and Kopp, P.E. (1999) Mathematics of Financial Market. Springer-Verlag, Brelin, Heidelberg, New York.
- Elliott, R.J. (1982) Stochastic Calculus and Applications. Springer-Verlag, Brelin, Heidelberg, New York.
- Hull, J. and White, A. (1995) Valuing Credit Default Swaps II: Modeling Default Correlations. Journal of Derivatives, 8, 12-21. http://dx.doi.org/10.3905/jod.2001.319153
- Kao, D.L. (2000) Estimating and Pricing Credit Risk: An Overview. Financial Analysts Journal, 56, 50-66. http://dx.doi.org/10.2469/faj.v56.n4.2373
- Nwozo, C.R. and Fadugba, S.E. (2012) Some Numerical Methods for Options Valuation. Communications in Mathematical Finance, 1, 51-74.
- Titman, S. and Torous, W. (1989) Valuing Commercial Mortgages: An Empirical Investigation of the Contingent Claims Approach to Pricing Risky Debt. Journal of Finance, 44, 345-373. http://dx.doi.org/10.2307/2328594
- Weiss, L.A. (1999) Bankrupty Resolution: Direct Costs and Violations of Priority of Claims. Journal of Financial Economics, 27, 251-272.
- Yang, L. and Zhiqiang, H. (2013) Monte Carlo Method for High-Tech Enterprise IPO Market Timing: Empirical Study Based on American Real Option Approach. International Journal of Applied Mathematics and Statistics, 44, 188-195.
- Wang, Z.G., Ou, Y.G. and Cai, B.G. (2012) Option Pricing Formula for Stock Model. International Journal of Applied Mathematics and Statistics, 27, 49-55.
- Madan, D.B. and Unal, H. (1998) Pricing the Risks of Default. Review of Derivatives Research, 2, 121-160. http://dx.doi.org/10.1007/BF01531333



















