Journal of Mathematical Finance
Vol.4 No.1(2014), Article ID:42222,8 pages DOI:10.4236/jmf.2014.41005
Game Russian Options for Double Exponential Jump Diffusion Processes
1Meijo University, Gifu, Japan
2Aoyama Gakuin University, Sagamihara, Japan
Email: *atsuo@urban.meijo-u.ac.jp, sawaki@si.aoyama.ac.jp
Received November 8, 2013; revised December 11, 2013; accepted December 27, 2013
ABSTRACT
In this paper, we deal with the valuation of Game Russian option with jumps, which is a contract that the seller and the buyer have both the rights to cancel and to exercise it at any time, respectively. This model can be formulated as a coupled optimal stopping problem. First, we discuss the pricing model with jumps when the stock pays dividends continuously. Secondly, we derive the value function of Game Russian options and investigate properties of optimal boundaries of the buyer. Finally, some numerical results are presented to demonstrate analytical properties of the value function.
Keywords:Stochastic Process; Game Russian Option; Double Exponential Distribution; Optimal Stopping; Optimal Boundaries
1. Introduction
Russian option was introduced by Shepp and Shiryaev [1,2] and it was one of perpetual American lookback options. In Russian option, the buyer has the right to exercise it at any time. On the other hand, in Game Russian option, not only the buyer but also the seller has the right to cancel it at any time. This option is based on Game option introduced by Kifer [3]. Game option frame work can be applied to various American-type options. Therefore, we apply this frame work to Russian option. The valuation of Game Russian option can be formulated as a coupled optimal stopping problem. See Cvitanic and Karatzas [4], Kifer [3].
Kyprianou [5] derived the closed-form solution in the case where the dividend rate is zero. Suzuki and Sawaki [6] gave the pricing formula with positive dividend. Kou and Wang [7] presented the closed-form for the value function of perpetual American put options without dividend and so on. Suzuki and Sawaki [8] studied the pricing formula of Russian option for double exponential jump diffusion processes.
In this paper, we deal with Game Russian options. Game Russian option is a contact that the seller and the buyer have the rights to cancel and to exercise it at any time, respectively. We present the pricing formula of Game Russian options for double exponential jump diffusion processes. The pricing of such an option can be formulated as a coupled optimal stopping problem which is analyzed as Dynkin game. We derive the value function of Game Russian option and its optimal boundaries. Also some numerical results are presented to demonstrate analytical sensitivities of the value function with respect to parameters.
This paper is organized as follows. In Section 2, we introduce a pricing model of Game Russian options by means of a coupled optimal stopping problem given by Kifer [3]. Section 3 presents the value function of Game Russian options for double exponential jump diffusion processes. Section 4 presents numerical examples to verify analytical results. We end the paper with some concluding remarks and future work.
2. Pricing Model
In this section, we consider the pricing model for Game Russian option. Let  be the process of the riskless asset price at time
be the process of the riskless asset price at time  defined by
defined by , where
, where 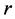 is the positive interest rate. Let
is the positive interest rate. Let  be a standard Brownian motion and
be a standard Brownian motion and  be a Poisson process with the intensity
be a Poisson process with the intensity . Let
. Let 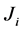 denote i.i.d. positive random variables.
denote i.i.d. positive random variables.  has a double exponential distribution and its density function is given by
has a double exponential distribution and its density function is given by

where 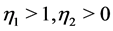 and
and 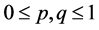 such that
such that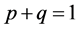 . Under a risk-neutral probability, the process of the risky asset price
. Under a risk-neutral probability, the process of the risky asset price 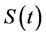 at time
at time 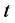 satisfies the stochastic differential equation
satisfies the stochastic differential equation
 (1)
(1)
where  and
and 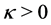 are constants. Define another probability measure
are constants. Define another probability measure 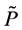 as
as

where  is a nonnegative continuous dividend rate of the risky asset,
is a nonnegative continuous dividend rate of the risky asset,
 is the information available at time
is the information available at time  and
and
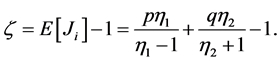
By Girsanov’s theorem,  is a Brownian motion with respect to
is a Brownian motion with respect to .
.
We can rewrite (1) as
 (2)
(2)
Solving (2) gives , where
, where
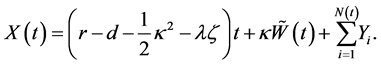
Let  be a function of class
be a function of class . Then the infinitesimal generator
. Then the infinitesimal generator 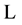 of the process
of the process  is given by
is given by
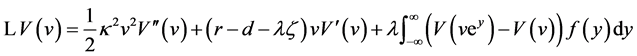
for all .
.
Next we introduce the four real numbers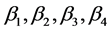 . Kou and Wang [9] showed that the equation
. Kou and Wang [9] showed that the equation  for all
for all  has the solutions
has the solutions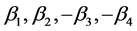 , where
, where
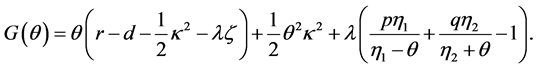
And the four solutions satisfy the following inequalities

Remark 2.1 When the dividend rate ,
,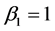 .
.
Define the process
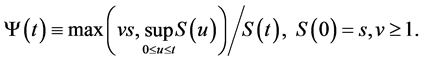
Then the value function of Russian option is given by
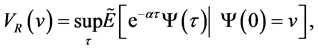
where the supremum is taken for all stopping times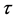 .
.
Theorem 2.1 (Suzuki and Sawaki [8]) The value function 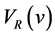 of Russian option with jump is given by
of Russian option with jump is given by
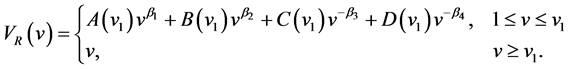
The coefficients are determined by

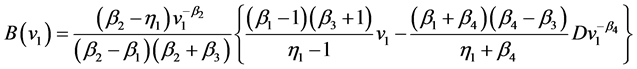
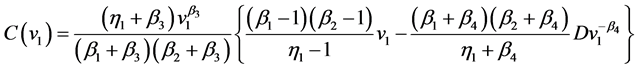
and
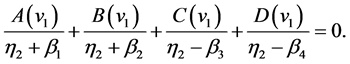
Moreover, the optimal boundary 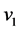 is the solution in
is the solution in  to the equation
to the equation
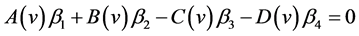
and the optimal stopping time is given by

3. Game Russian Options
Let 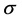 denote a cancel time for the seller and
denote a cancel time for the seller and 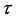 an exercise time for the buyer. If the seller cancels the contract, the buyer receives
an exercise time for the buyer. If the seller cancels the contract, the buyer receives  from the seller. We can think of
from the seller. We can think of 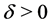 as the penalty cost for the cancellation. On the other hand, if the buyer exercises it, (s)he receives
as the penalty cost for the cancellation. On the other hand, if the buyer exercises it, (s)he receives  from the seller. Therefore, the payoff function for the buyer is given by
from the seller. Therefore, the payoff function for the buyer is given by

Let 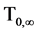 denote the set of all stopping times with values in the interval
denote the set of all stopping times with values in the interval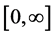 . Then the value function
. Then the value function 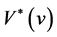 of Game Russian option is defined by
of Game Russian option is defined by
 (3)
(3)
where
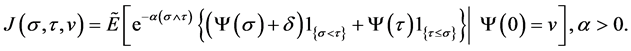
And the function 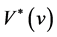 satisfies the inequalities
satisfies the inequalities
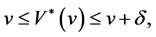
which provides the lower and the upper bounds for the value function of Game Russian option.
We define two sets 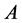 and
and 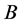 as
as


 and
and  are called the seller’s cancellation region and the buyer’s exercise region, respectively. Then the two optimal stopping times are given by
are called the seller’s cancellation region and the buyer’s exercise region, respectively. Then the two optimal stopping times are given by
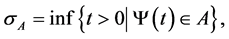

Then for any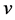 ,
,  and
and 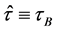 attain the infimum and supremum in (3), i.e., we have
attain the infimum and supremum in (3), i.e., we have
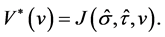
The pair  is the saddle point of
is the saddle point of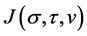 .
.
Remark 3.1 The seller minimizes the payoff function and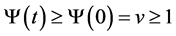 . From this, it follows that the seller’s optimal cancellation region is
. From this, it follows that the seller’s optimal cancellation region is .
.
Lemma 3.1 Suppose that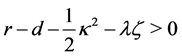 . Then the function
. Then the function 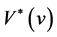 is Lipschitz continuous and its Radon-Nikodym derivative satisfies
is Lipschitz continuous and its Radon-Nikodym derivative satisfies
 (4)
(4)
Proof. Since 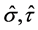 and
and 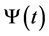 depend on the initial value
depend on the initial value , we write them as
, we write them as  and
and . Replacing the optimal stopping times
. Replacing the optimal stopping times 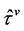 by another stopping time
by another stopping time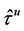 , we get the inequalities
, we get the inequalities

Note that  for any
for any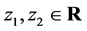 . For any
. For any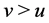 , we have
, we have
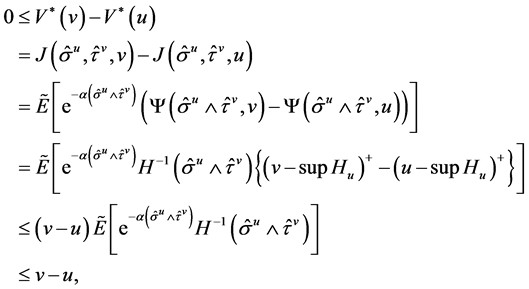
where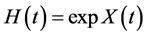 . Therefore, we obtain
. Therefore, we obtain
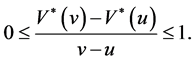
This means that  is Lipschitz continuous and satisfies (4).
is Lipschitz continuous and satisfies (4).
If the penalty 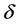 is large enough, the seller never cancels. It is of interest to show how much
is large enough, the seller never cancels. It is of interest to show how much 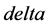 should be large for the seller never to cancel.
should be large for the seller never to cancel.
Lemma 3.2 Set . If the penalty
. If the penalty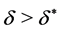 , the seller never cancels. In other words, Game Russian option is reduced to Russian option.
, the seller never cancels. In other words, Game Russian option is reduced to Russian option.
Proof. Consider the function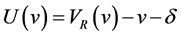 . Since it holds
. Since it holds  by Lemma 3.1 and
by Lemma 3.1 and
 , we have
, we have . Hence, it follows that
. Hence, it follows that  because the inequality
because the inequality 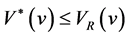 holds.
holds.
We assume that  and
and . It means that the jump occurs only upward. This is very useful to analyse stochastic cash management problem for jump diffusion processes (See Sato and Suzuki [10]). Then we can express
. It means that the jump occurs only upward. This is very useful to analyse stochastic cash management problem for jump diffusion processes (See Sato and Suzuki [10]). Then we can express  as
as

and the equation  has three solutions
has three solutions , which satisfy
, which satisfy

We introduce the function for 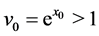
 (5)
(5)
We set  and
and . In what follows, we determine the coefficients
. In what follows, we determine the coefficients  and
and . In order to determine the coefficients, we prepare the conditions. By value matching condition, we have
. In order to determine the coefficients, we prepare the conditions. By value matching condition, we have
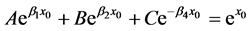
and by smooth pasting condition, we have
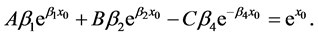
We can get the last condition by using the infinitesimal generator  of the process
of the process  given by
given by

for all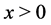 . For
. For , we obtain
, we obtain
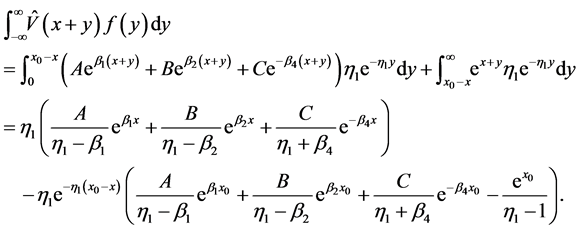
From this, we obtain

where . By Lemma 2.1 in Kou and Wang [9], we have
. By Lemma 2.1 in Kou and Wang [9], we have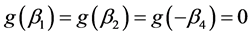 . Since
. Since
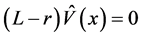 holds, we get the condition
holds, we get the condition
 (6)
(6)
Lemma 3.3 Solving the following equations
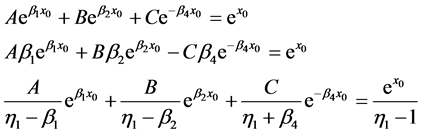
gives the solutions

Since the coefficients  depend on
depend on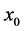 , we denote them as
, we denote them as  and
and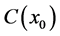 . The number
. The number 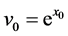 given by (5) satisfies the equation
given by (5) satisfies the equation
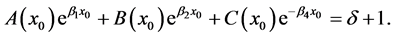
4. Main Theorem
Theorem 4.1 Let  denote the value function of Game Russian option. If
denote the value function of Game Russian option. If , the value function is equal to the one of Russian option, i.e.
, the value function is equal to the one of Russian option, i.e. . If
. If , then
, then 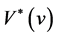 is given by
is given by
 (7)
(7)
and the optimal stopping times are given by


The optimal boundary  for the buyer is the unique solution to the equation
for the buyer is the unique solution to the equation

In order to prove the above theorem, we need the following lemmas.
Lemma 4.1 Assume that a function  has the following properties;
has the following properties;
1) 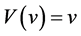 and
and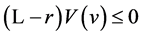 , for
, for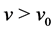 .
.
2) It holds 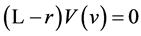 and
and 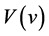 satisfies
satisfies  for
for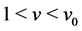 .
.
3) At 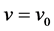 we have
we have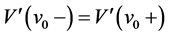 .
.
Then, 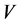 is the value function of Game Russian options with dividend, i.e.,
is the value function of Game Russian options with dividend, i.e., 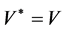 holds. The optimal exercise region is the interval
holds. The optimal exercise region is the interval  and the optimal cancellation region is
and the optimal cancellation region is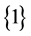 .
.
Proof. By Ito’s formula, we have
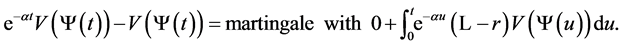 (8)
(8)
Set

and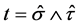 . Since
. Since 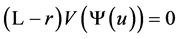 a.s. for
a.s. for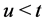 , we have
, we have 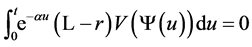 a.s. Therefore, taking expectation of (8), we have
a.s. Therefore, taking expectation of (8), we have
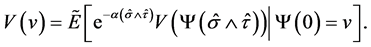
It holds
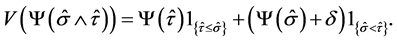
Therefore we get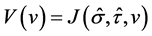 .
.
For any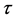 , set
, set . The term of
. The term of 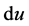 is nonpositive a.s. because
is nonpositive a.s. because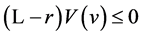 . Taking expectation of (8), we get
. Taking expectation of (8), we get

The above left hand side dominates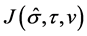 . Therefore
. Therefore
 (9)
(9)
Next for any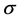 , set
, set . Similarly it holds
. Similarly it holds

Since the left hand side is dominated by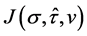 , we get
, we get
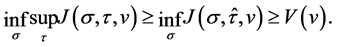 (10)
(10)
From (9) and (10), we have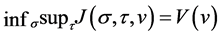 .
.
Lemma 4.2 The function  satisfies
satisfies 
Proof. Since  for
for , we have
, we have

Hence, we obtain
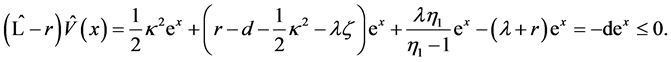
That is, we obtain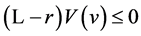 .
.
Lemma 4.3 For 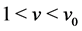 the function
the function 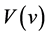 satisfies
satisfies 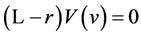 and
and
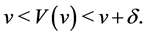
Proof. The former assertion is known. We shall show the latter one. The second derivative of 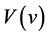 is nonnegative because
is nonnegative because  and
and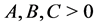 . It follows that
. It follows that 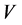 is a convex function. Since
is a convex function. Since 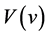 is a convex function,
is a convex function, 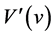 is increasing. From this, we can see that
is increasing. From this, we can see that  for
for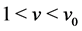 . By the boundary conditions
. By the boundary conditions 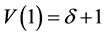 and
and , we have
, we have .
.
Lemma 4.4 Set
 (11)
(11)
Then the equation  has the unique solution in the interval
has the unique solution in the interval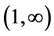 .
.
Proof. By (11), a direct computation yields
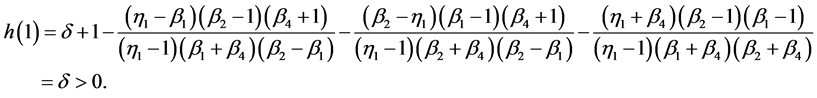
Since  and
and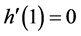 , we have
, we have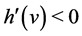 . Furthermore, it holds
. Furthermore, it holds . Therefore, the equation
. Therefore, the equation  has the unique solution in
has the unique solution in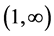 .
.
In the rest of this section, we present some numerical examples to demonstrate theoretical results and some effects of parameters on the price of Game Russian option. We set 
 . Using these parameters,
. Using these parameters, 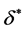 is 0.248.
is 0.248.
Figure 1 shows how the optimal exercise boundary increase as the penalty 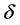 increases from 0.1 up to
increases from 0.1 up to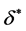 . From the figure, we can see that the optimal boundary
. From the figure, we can see that the optimal boundary 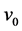 is increasing in the penalty
is increasing in the penalty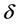 . Figure 2 demonstra-
. Figure 2 demonstra-

Figure 1. Optimal boundary for the buyer.
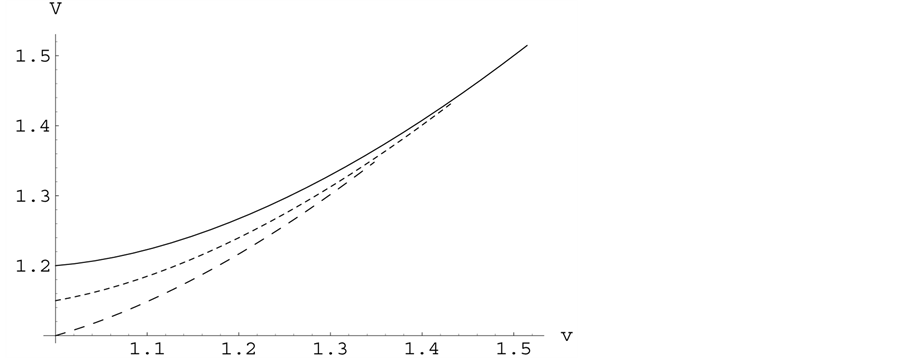
Figure 2. The value function.
tes the value function of Game Russian option with jumps. Dashed lines represent the graph of the value 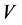 in
in 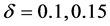 from the bottom, respectively. Real line represents the value in
from the bottom, respectively. Real line represents the value in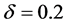 . From Figure 2, we can visually recognize that
. From Figure 2, we can visually recognize that  is convex and increasing in
is convex and increasing in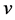 .
.
5. Conclusion
In this paper, we discussed the valuation of Game Russian option written on dividend paying asset, obtained the value function of it for double exponential jump diffusion processes and also explored some analytical properties of the value function and the optimal boundaries for the seller and buyer, which were useful to provide an approximation of the finite lived Game Russian option. Moreover, we plan to examine convertible bonds with jumps by using Game option frame work. We shall leave it as future work.
REFERENCES
- Shepp, L.A. and Shiryaev, A.N. (1993) The Russian option: Reduced regret. The Annals of Applied Probability, 3, 631-640. http://dx.doi.org/10.1214/aoap/1177005355
- Shepp, L.A. and Shiryaev, A.N. (1994) A new look at pricing of the “Russian option”. Theory of Probability and Its Applications, 39, 103-119. http://dx.doi.org/10.1137/1139004
- Kifer, Y. (2000) Game options. Finance and Stochastics, 4, 443-463. http://dx.doi.org/10.1007/PL00013527
- Cvitanic, J. and Karatzas, I. (1996) Backward stochastic differential equations with reflection and Dynkin games. The Annals of Probability, 24, 2024-2056. http://dx.doi.org/10.1214/aop/1041903216
- Kyprianou, A.E. (2004) Some calculations for Israeli options. Finance and Stochastics, 8, 73-86. http://dx.doi.org/10.1007/s00780-003-0104-5
- Suzuki, A. and Sawaki, K. (2009) The pricing of callable Russian options and their optimal boundaries. Journal of Applied Mathematics and Decision Sciences, 2009, Article ID: 593986, 13 p. http://dx.doi.org/10.1155/2009/593986
- Kou, S.G. and Wang, H. (2004) Option pricing under a double exponential jump diffusion model. Management Science, 50, 1178-1192. http://dx.doi.org/10.1287/mnsc.1030.0163
- Suzuki, A. and Sawaki, K. (2010) The valuation of Russian options for double exponential jump diffusion processes. Asia Pacific Journal of Operational Research, 27, 227-242.
- Kou, S.G. and Wang, H. (2003) First passage times for a jump diffusion process. Advances in Applied Probability, 35, 504-531. http://dx.doi.org/10.1239/aap/1051201658
- Sato, K. and Suzuki, A. (2011) Stochastic cash management problem with double exponential jump diffusion processes. Lecture Notes in Operations Research, 14, 186-194.
NOTES

*Corresponding author.

