Journal of Mathematical Finance
Vol.3 No.4(2013), Article ID:38146,6 pages DOI:10.4236/jmf.2013.34045
Variance Reduction Techniques of Importance Sampling Monte Carlo Methods for Pricing Options*
1School of Finance, Shanghai University of Finance and Economics, Shanghai, China
2Department of Applied Mathematics, Shanghai University of Finance and Economics, Shanghai, China
Email: qiangcho@gmail.com
Copyright © 2013 Qiang Zhao et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 10, 2013; revised September 7, 2013; accepted September 18, 2013
Keywords: Monte Carlo Method; Importance Sampling; Variance Reduction; Option Pricing
ABSTRACT
In this paper we discuss the importance sampling Monte Carlo methods for pricing options. The classical importance sampling method is used to eliminate the variance caused by the linear part of the logarithmic function of payoff. The variance caused by the quadratic part is reduced by stratified sampling. We eliminate both kinds of variances just by importance sampling. The corresponding space for the eigenvalues of the Hessian matrix of the logarithmic function of payoff is enlarged. Computational Simulation shows the high efficiency of the new method.
1. Introduction
Monte Carlo simulation is a numerical method based on the probability theory. Its application in finance becomes more and more popular as the demand for pricing and hedging of various complex financial derivatives, which play an important role in the field of investment, risk management and corporate governance. The advantage of Monte Carlo method is that its convergence rate is independent on the number of state variables. Monte Carlo simulation is often the only way available for the pricing of complex path-dependent options if the number of relevant underlying assets is greater than three. However, Monte Carlo simulation is constantly criticized for its slow convergence. Let 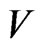 be a random variable and we want to calculate
be a random variable and we want to calculate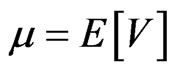 . We can generate independently and identically distributed samples
. We can generate independently and identically distributed samples 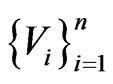 of
of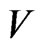 . Law of Large Numbers guarantees that
. Law of Large Numbers guarantees that

and Central Limit Theorem guarantees that 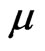 asymptotically falls in the confidence interval
asymptotically falls in the confidence interval
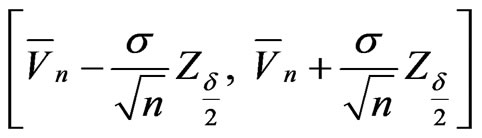
with probability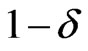 , where
, where  is the standard deviation of
is the standard deviation of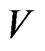 ,
,  is the number of samples,
is the number of samples,  is the significance level and
is the significance level and 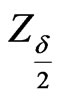 is the quantile of standard normal distribution under
is the quantile of standard normal distribution under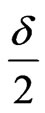 .
.
It is clear that the convergence rate of Monte Carlo method is
 .
.
hence, in order to reduce the error by a factor of 10 one has to generate 100 times as much as samples as well as computation time. For this reason, Monte Carlo simulation needs to be run on large parallel computers with a high financial cost in terms of hardware and software developments. The computational demands of simulation have motivated substantial interest in the financial industry in demands for increased efficiency. Another way to improve the accuracy is to reduce the standard deviation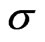 . Motivated by this thought, several techniques to reduce the variance of the Monte Carlo simulation have been proposed, such as control variates, antithetic variables, importance sampling and stratification(see Boyle, Broadie and Glasserman [1], and Glasserman [2]. These techniques aim to reduce the variance per Monte Carlo observation so that a given level of accuracy can be obtained with a smaller number of simulations. Control variates and antithetic variables are the most widely used variance reduction techniques, mainly because of the simplicity of their implementations, and the fact that they can be accommodated in an existing Monte Carlo calculator with a small effort. Examples of successful implementations of control variates for pricing the derivatives include Hull and White [3], Kemna and Vorst [4], Turnbull and Wakeman [5], Ma and Xu [6].
. Motivated by this thought, several techniques to reduce the variance of the Monte Carlo simulation have been proposed, such as control variates, antithetic variables, importance sampling and stratification(see Boyle, Broadie and Glasserman [1], and Glasserman [2]. These techniques aim to reduce the variance per Monte Carlo observation so that a given level of accuracy can be obtained with a smaller number of simulations. Control variates and antithetic variables are the most widely used variance reduction techniques, mainly because of the simplicity of their implementations, and the fact that they can be accommodated in an existing Monte Carlo calculator with a small effort. Examples of successful implementations of control variates for pricing the derivatives include Hull and White [3], Kemna and Vorst [4], Turnbull and Wakeman [5], Ma and Xu [6].
Importance sampling has the capacity to exploit detailed knowledge about a model (often in the form of asymptotic approximations) to produce potential variance reduction. Unfortunately, importance sampling technique has not been widely used as other variance reduction techniques in pricing financial derivatives until recently. This is mainly because there is no general way to implement importance sampling. If the transformation of probability measure is chosen improperly, this method does not work. Importance sampling attempts to reduce variance by changing the probability measure from which paths are generated. Our goal is to obtain a more convenient representation of the expected value. The idea behind the importance sampling is to reduce the statistical uncertainty of Monte Carlo calculation by focusing on the most important region of the space from which the random samples are drawn. Such regions depend both on the random process simulated, and the structure of the security priced. Just as mentioned by Glasserman [2], an effective importance sampling density should weight more points to the region where the product of their probability and their payoff is large. For example, for a deep out-of-the-money call option, most of the time the payoff from simulation is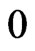 , so simulating more paths with positive payoffs should reduce the variance in the estimation.
, so simulating more paths with positive payoffs should reduce the variance in the estimation.
An early example of importance sampling applied to security pricing is Reider [7], where the variance was reduced substantially by increasing the drift in simulation for deep out-of-the-money European call options. Glasserman, Heidelberger and Shahabuddin [8] applied importance sampling to reduce substantial variance by combining stratification in the stochastic volatility model. Other recent work on importance sampling methods in finance has been done for Monte Carlo simulations driven by high-dimensional Gaussian vectors, such as Boyle, Broadie and Glasserman [1], Vázquez-Abad and Dufresne [9], Su and Fu [10], Arouna [11], Capriotti [12]Xu and Zhang [13]. In this framework, Importance Sampling is applied by modifying the drift term of the simulated process to construct a new measure in which more weight is given to important outcomes thereby increasing sampling efficiency. The different methods proposed in the literature mainly differ in the way where such a change of drift is found, and can be divided into two families based on the strategy adopted. The first one is proposed by Glasserman, Heidelberge and Shahabuddin in a remarkable paper [14] (GHS for short), relies on a deterministic optimization procedure which can be applied for a specific class of payoffs. Xu and Zhang [13] improve the optimization algorithm of the importance sampling by Newton Raphson algorithm based on direct simulation. The second one is the so-called adaptive Monte Carlo method, such as Vázquez-Abad and Dufresne [9], Su and Fu [10], Arouna [11], that aims to determine the optimal drift through stochastic optimization techniques that typically involve an iterative algorithm.
Most closely related to our work is Glasserman, Heidelberge and Shahabuddin [14], who applied importance sampling combined with stratified sampling to dramatically reduce variance in derivative pricing. In this paper, we propose a new importance sampling method by modifying the drift term and the quadratic term of the simulated process simultaneously. In the previous literature, the variance for the linear part is eliminated by importance sampling and those for the quadratic part is reduced by stratification. However, we eliminate both kinds of variances just by importance sampling. The corresponding space for the eigenvalues of the Hessian matrix of the log function of payoff is enlarged. Illustrations of the use of the method with European options and Asian options are given, which show the high efficiency of the method. The method proposed in the paper can be extended to the pricing of other financial derivaives directly.
2. Importance Sampling Method
Importance sampling attempts to reduce variance by changing the probability measure from which samples are generated. To make this idea concrete, consider the problem of estimating
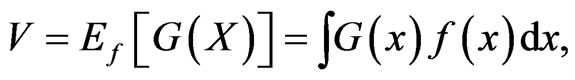 (1)
(1)
where  is a random vector of
is a random vector of 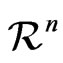 with probability density
with probability density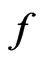 , and
, and 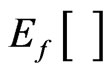 denotes the expectation under the original measure with density function
denotes the expectation under the original measure with density function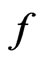 ,
,  is a function from
is a function from 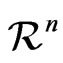 to
to , generally denoting the payoffs of financial derivatives. The ordinary Monte Carlo estimator is
, generally denoting the payoffs of financial derivatives. The ordinary Monte Carlo estimator is
 (2)
(2)
with 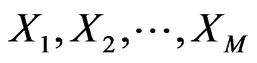 independent draws from
independent draws from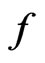 . Let
. Let 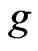 be any other probability density on
be any other probability density on 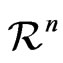 satisfying
satisfying
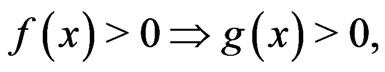 (3)
(3)
for all . Then we can obtain by changing measure
. Then we can obtain by changing measure
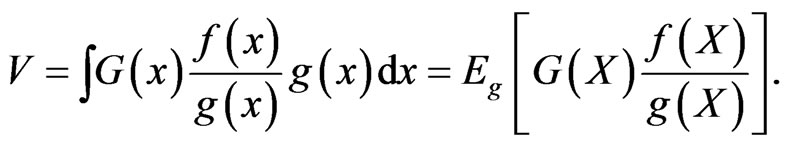 (4)
(4)
Thus, 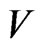 can be interpreted as an expectation with respect to the density
can be interpreted as an expectation with respect to the density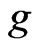 .
.
If  are now independent draws from
are now independent draws from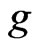 , the importance sampling estimator associated with
, the importance sampling estimator associated with 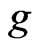 is
is
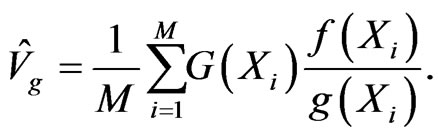 (5)
(5)
The weight

is the likelihood ratio evaluated at .
.
It follows from (1) and (4) that

and thus both  and
and  are unbiased estimators of
are unbiased estimators of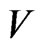 . To compare variances with and without importance sampling it suffices to compare their second moments. With importance sampling we have
. To compare variances with and without importance sampling it suffices to compare their second moments. With importance sampling we have
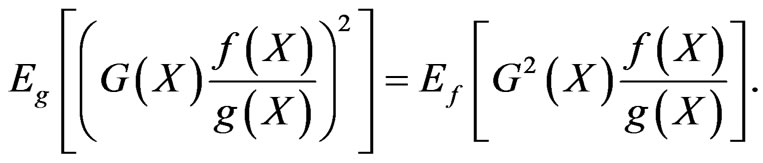 (6)
(6)
Depending on the choice of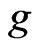 , this could be larger or smaller than the second moment
, this could be larger or smaller than the second moment 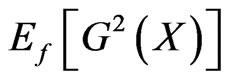 without importance sampling. Successful importance sampling lies on the art of selecting an effective importance sampling density
without importance sampling. Successful importance sampling lies on the art of selecting an effective importance sampling density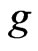 .
.
From (2), the variance of  is
is
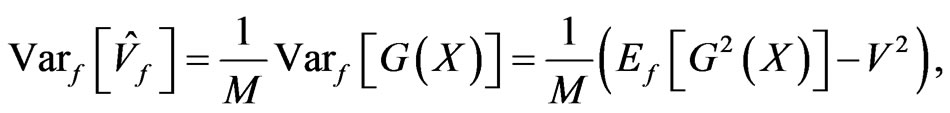
where  denotes the variance under the measure with density function
denotes the variance under the measure with density function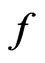 . Similarly, from (5) and (6), the variance of
. Similarly, from (5) and (6), the variance of  is
is
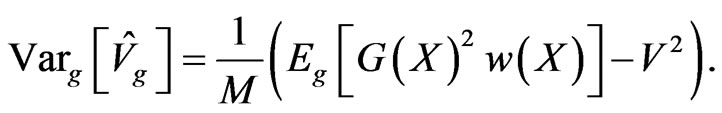
In particularly, if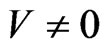 , a zero-variance estimate is thus obtained by choosing
, a zero-variance estimate is thus obtained by choosing
 (7)
(7)
We call this function as the optimal density function. This choice of density is precluded unless the estimated quantity 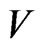 is known from the outset. Nevertheless, this observation provides a useful insight: An effective importance sampling density should weight points according to the product of their probability and payoff.
is known from the outset. Nevertheless, this observation provides a useful insight: An effective importance sampling density should weight points according to the product of their probability and payoff.
Generally, the key of importance sampling lies to find  satisfying (3) to solve the following optimal problem,
satisfying (3) to solve the following optimal problem,
 (8)
(8)
Unfortunately, there is no general way to find the optimal 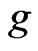 for an ordinary function
for an ordinary function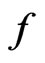 . So, we turn to find the relatively optimal
. So, we turn to find the relatively optimal  to make the variance as small as possible.
to make the variance as small as possible.
3. New Importance Sampling Simulation
In this section, we propose a new importance sampling simulation following the idea of GHS. Consider the problem of estimating the expectation of the payoff

where 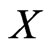 is a
is a  -dimensional vector of standard normal variable with probability density
-dimensional vector of standard normal variable with probability density
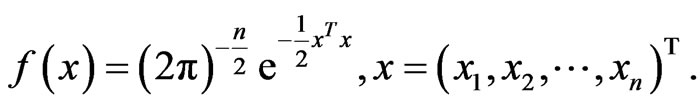
when choosing the new probability function, the previous literature featuring GHS has only taken drift into consideration. They choose drift 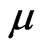 satisfying
satisfying
 (9)
(9)
where
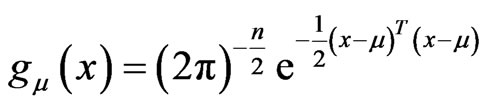 .
.
Based on GHS’s idea, we take both drift and variance term into consideration. If the covariance matrix  is positive definite, we can choose
is positive definite, we can choose
 (10)
(10)
thus, we obtain by changing measure
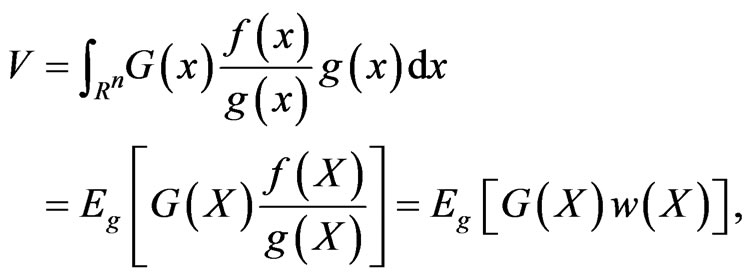 (11)
(11)
where the likelihood ratio is

Note that the covariance matrix  is positive definite, there exists a nonsingular
is positive definite, there exists a nonsingular  -dimensional matrix
-dimensional matrix  satisfying
satisfying .
.
If
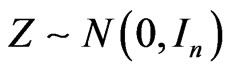 and
and
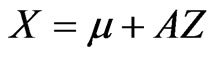 then
then
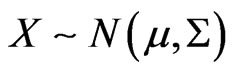 .
.
Denote
 where
where
 .
.
It follows that
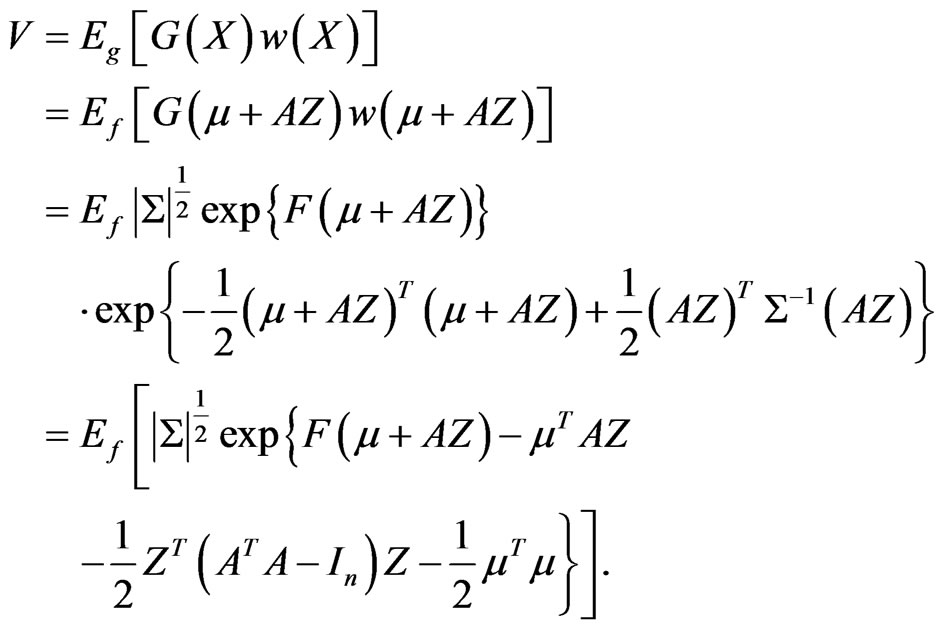 (12)
(12)
Suppose that 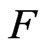 is twice continuously differentiable on
is twice continuously differentiable on , a second-order Taylor expansion formula shows
, a second-order Taylor expansion formula shows
 (13)
(13)
By (12) and (13), we have
 (14)
(14)
We can choose 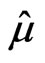 and
and 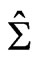 satisfying
satisfying
 (15)
(15)
and
 (16)
(16)
where we assume that all the eigenvalues of the Hessian matrix 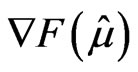 are less than
are less than . (Following the analysis of Rogers and Talay [15], the condition is satisfied for most of options including Asian option, barrier option and various path-dependent options with stochastic volatility.)
. (Following the analysis of Rogers and Talay [15], the condition is satisfied for most of options including Asian option, barrier option and various path-dependent options with stochastic volatility.)
(15) can be solved using iteration method in GHS. Then,  is easily obtained by direct substitution of
is easily obtained by direct substitution of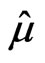 . So the linear and quadratic part of the function
. So the linear and quadratic part of the function 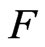 is removed. Our choice of drift vector and variance matrix may be viewed as eliminating the variance contribution due to the linear and the quadratic part of
is removed. Our choice of drift vector and variance matrix may be viewed as eliminating the variance contribution due to the linear and the quadratic part of . We consider the new density function
. We consider the new density function
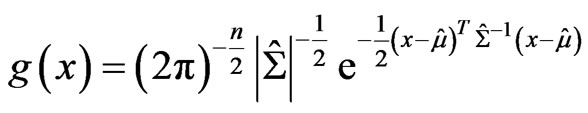 (17)
(17)
as a proper measure transformation. Finally, the new estimator with smaller variance can be obtained by (5).
In GHS, the variance caused by the quadratic part of 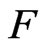 is reduced by use of stratification which needs relatively complicated numerical calculation. Meanwhile, the efficiency of the stratification demands that all the eigenvalues of the Hessian matrix of
is reduced by use of stratification which needs relatively complicated numerical calculation. Meanwhile, the efficiency of the stratification demands that all the eigenvalues of the Hessian matrix of  at the value
at the value 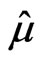
are less than . Obviously, the new method can be applied to more types of financial derivatives.
. Obviously, the new method can be applied to more types of financial derivatives.
4. Numerical Simulation
In this section, we illustrate the results developed in the previous sections. We use two examples in which we compare our method with GHS method to reveal the efficiency of the new method.
In the Black-Scholes model, the price of underlying asset 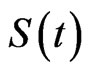 obeys
obeys
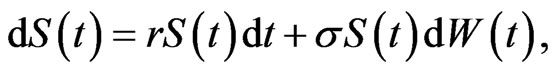 (18)
(18)
where 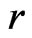 is the risk free rate,
is the risk free rate, 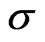 is the volatility and
is the volatility and 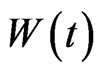 is a standard Brownian motion.
is a standard Brownian motion.
Suppose that 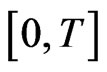 is the valid period of the option and
is the valid period of the option and 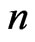 is the number of observations,
is the number of observations,  are the observation dates and
are the observation dates and 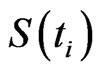 is the price of the underlying asset at the
is the price of the underlying asset at the  th observation date.
th observation date.
The underlying asset can be simulated by
 (19)
(19)
where
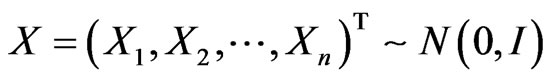 .
.
For simplicity, we set
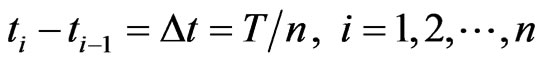 .
.
Experiment 1: Consider European call option under the Black-Scholes model. The discounted payoff function is
 .
.
We set 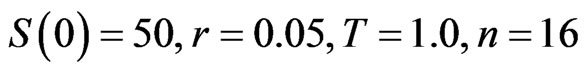 and use
and use 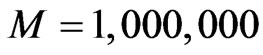 paths to estimate the variance reduction ratio between
paths to estimate the variance reduction ratio between 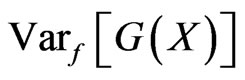 and
and . The numerical results are illustrated in table 1.
. The numerical results are illustrated in table 1.
Numerical results in table 1 show estimated prices and variance ratios, relative to ordinary Monte Carlo method, using importance sampling with GHS method and the new method respectively, which confirm the effectiveness of the procedure for this problem, especially for in-the-money options. Variance reduction ratio is the variance per replication using standard Monte Carlo method divided by the variance per replication using the above two methods. The large ratio, the great the improvement.
In Figure 1, the optimal density denotes the density represented by (7). The GHS density figure can be obtained through translating the original density figure right by . After modifying the quadratic term, we can change the shape of the GHS density figure and get the new density figure. Obviously, the new density figure is closer to the optimal one than the GHS density figure, thus achieving greater variance reduction.
. After modifying the quadratic term, we can change the shape of the GHS density figure and get the new density figure. Obviously, the new density figure is closer to the optimal one than the GHS density figure, thus achieving greater variance reduction.
Experiment 2: As a typical test case treated in recent papers, we will consider arithmetic Asian call option. The discounted payoff function is
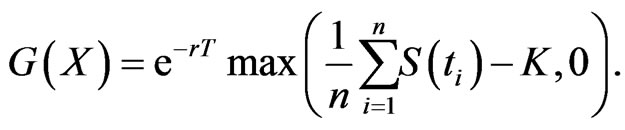
We set  and use
and use  paths to estimate the variance reduction ratio between
paths to estimate the variance reduction ratio between 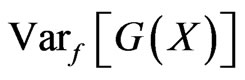 and
and . The numerical results are illustrated in tables 2-6.
. The numerical results are illustrated in tables 2-6.
These tables above show the simulation results for different volatilities and strike prices. Firstly, GHS method achieves larger variance ratios when the option is deeper out of money, which coincides with results in Reider [7]. For a deep out-of-money Call option, most paths with zero payoff are sampled in simulation. By changing the drift of sampling density, a large part of zero-payoff paths are replaced by positive-payoff paths. Hence, simulating more samples with positive payoff reduces the variance. The effect of variance reduction by changing the drift will be strengthened or weakened by changing the form of the sampling density figure.

Table 1. Estimated variance reduction ratios for European call option.

Figure 1. Sampling probability density function for European call option with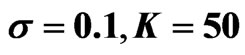 .
.
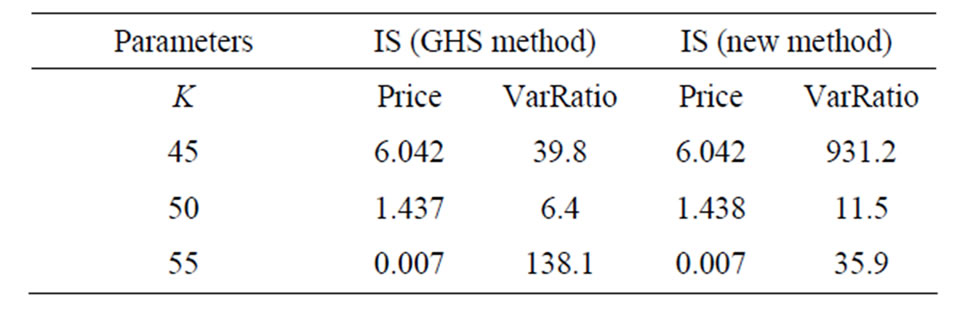
Table 2. Estimated variance reduction ratios for arithmetic Asian call option with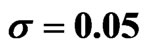 .
.

Table 3. Estimated variance reduction ratios for arithmetic Asian call option with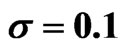 .
.
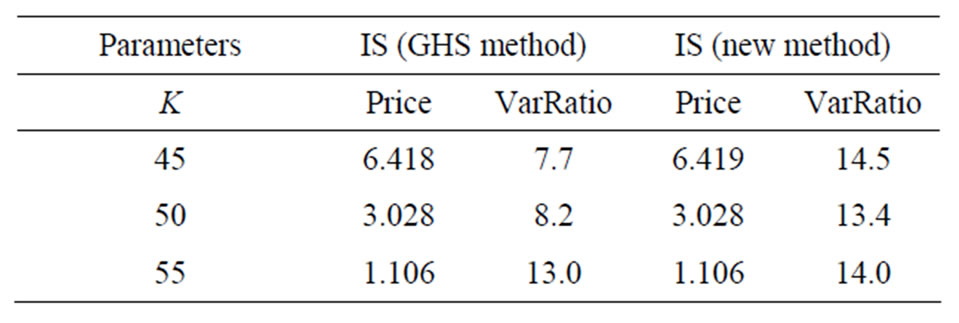
Table 4. Estimated variance reduction ratios for arithmetic Asian call option with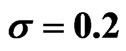 .
.
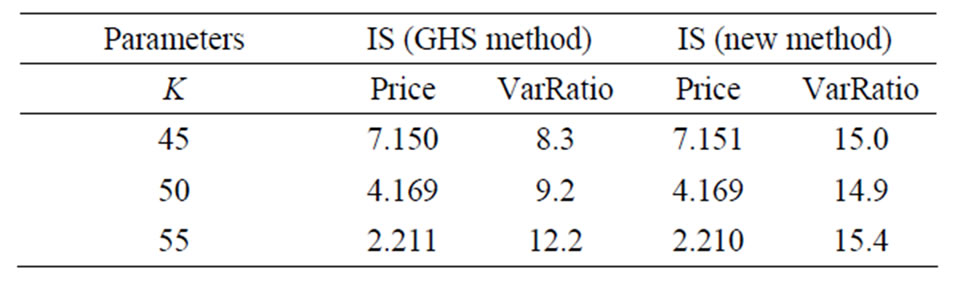
Table 5. Estimated variance reduction ratios for arithmetic Asian call option with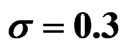 .
.
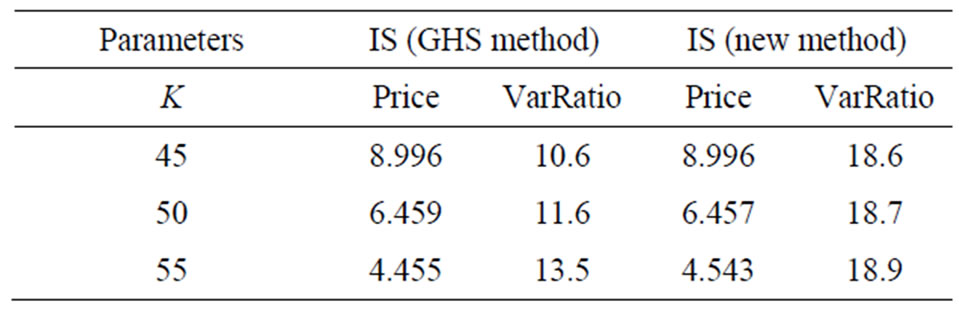
Table 6. Estimated variance reduction ratios for arithmetic Asian call option with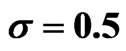 .
.
Secondly, for an in-the-money option, the new method achieves larger variance ratios than the GHS method. With the decrease of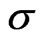 , the superiority becomes obvious. This is because the fact that most paths with positive payoff are sampled when simulating an in-themoney option makes it ineffective just by changing the drift. When the volatility
, the superiority becomes obvious. This is because the fact that most paths with positive payoff are sampled when simulating an in-themoney option makes it ineffective just by changing the drift. When the volatility  gets smaller, the underlying asset changes more slow so that most payoffs are positive. This leads to the GHS method in vain and makes the new method effective.
gets smaller, the underlying asset changes more slow so that most payoffs are positive. This leads to the GHS method in vain and makes the new method effective.
Thirdly, for an out-of-the-money option, the GHS method performs better than the new method especially when the volatility 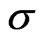 is small. In this case, by changing the drift, most paths with zero payoff are replaced by nonzero-payoff paths, leaves no room for more variance reduction by changing the form of the sampling density function.
is small. In this case, by changing the drift, most paths with zero payoff are replaced by nonzero-payoff paths, leaves no room for more variance reduction by changing the form of the sampling density function.
5. Concluding Remarks
In this paper, a new importance sampling Monte Carlo method for pricing options is proposed. Unlike the classical importance sampling procedure, both kinds of variance caused by the linear part and the quadratic part of the logarithmic function of payoff are eliminated. The corresponding space for the eigenvalues of the Hessian matrix of the logarithmic function of payoff is enlarged. Computational Simulation shows the high efficiency of the new method.
REFERENCES
- P. Boyle, M. Broadie and P. Glasserman, “Monte Carlo Methods for Security Pricing,” Journal of Economic Dynamic and Control, Vol. 21, No. 8, 1997, pp.1267-1321. http://dx.doi.org/10.1016/S0165-1889(97)00028-6
- P. Glasserman, “Monte Carlo Methods in Financial Engineering,” Springer-Verlag, New York, 2004.
- J. Hull and A. White, “The Use of the Control Variate Technique in Option Pricing,” Journal of Financial and Quantitative Analysis, Vol. 23, No. 3, 1987, pp. 237-251. http://dx.doi.org/10.2307/2331065
- A. G. Kemna and A. C. F. Vorst, “A Pricing Method for Options Based on Average Asset Values,” Journal of Banking & Finance, Vol. 14, No. 1, 1990, pp. 113-129. http://dx.doi.org/10.1016/0378-4266(90)90039-5
- S. Turnbull and L. Wakeman, “A Quick Algorithm for Pricing European Average Options,” Journal of Financial and Quantitative Analysis, Vol. 26, No. 3, 1991, pp. 377- 389. http://dx.doi.org/10.2307/2331213
- J. Ma and C. Xu, “An Efficient Control Variate Method for Pricing Variance Derivatives under Stochastic Volatility and Jump Diffusion Models,” Journal of Computational and Applied Mathematics, Vol. 235, No. 1, 2010, pp. 108-119. http://dx.doi.org/10.1016/j.cam.2010.05.017
- R. Reider, “An Efficient Monte Carlo Technique for Pricing Options,” Working Paper, Wharton School, University of Pennsylvania, Philadelphia, 1993.
- P. Glasserman, P. Heidelberger and P. Shahabuddin, “Importance Sampling in the Heath-Jarrow-Morton Framework,” Journal of Derivatives, Vol. 7, No. 1, 1999, pp. 32-50. http://dx.doi.org/10.3905/jod.1999.319109
- F. J. Vázquez-Abad and D. Dufresne, “Accelerated Simulation for Pricing Asian Options,” Proceedings of 1998 Winter Simulation Conference, Washington DC, 13-16 December 1998, pp. 1493-1500. http://dx.doi.org/10.1109/WSC.1998.746020
- Y. Su and M. C. Fu, “Simulation in Financial Engineering: Importance Sampling in Derivative Securities Pricing,” Proceedings of the 32nd Conference on Winter Simulation, Society for Computer Simulation International, 2000, pp. 587-596.
- B. Arouna, “Robbins-Monro Algorithms and Variance Reduction in Finance,” Journal of Computational Finance, Vol. 7, No. 2, 2004, pp. 35-62.
- L. Capriotti, “Least-squares Importance Sampling for Monte Carlo Security Pricing,” Quantitative Finance, Vol. 8, No. 5, 2008, pp. 485-497. http://dx.doi.org/10.1080/14697680701762435
- C. Xu and L. Zhang, “On Optimal Drift Vector and Importance Sampling for Pricing Options Based on Direct Simulations,” Working Paper, 2011.
- P. Glasserman, P. Heidelberger and P. Shahabuddin, “Asymptotically Optimal Importance Sampling and Stratification for Pricing Path-Dependent Options,” Mathematical Finance, Vol. 9, No. 2, 1999, pp. 117-152. http://dx.doi.org/10.1111/1467-9965.00065
- L. C. G. Rogers and D. Talay, “Numerical Methods in Finance,” Cambridge University Press, Cambridge, 1997. http://dx.doi.org/10.1017/CBO9781139173056
NOTES
*This work is supported by Research Innovation Foundation of Shanghai University of Finance and Economics under Grant No. CXJJ-2013- 323; Basic Academic Discipline Program, the 11th five year plan of 211 Project for Shanghai University of Finance and Economics.

