Open Journal of Safety Science and Technology
Vol.4 No.2(2014), Article
ID:47277,8
pages
DOI:10.4236/ojsst.2014.42013
About the Causes of the Koror Bridge Collapse
Corneliu Bob
University “Politehnica” of Timisoara, Timisoara, Romania
Email: cbob@mail.dnttm.ro
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2014; revised 25 May 2014; accepted 23 June 2014
ABSTRACT
This paper has been prepared from basic works published, mainly, after 2008 when the collapse investigation was made available. The main contributions of the paper are: a proper model for the deflections at mid-span of the bridge, the state of stress in elastic and post elastic stage for same phases of behavior, the stage of cracked of the top of cantilever beams, the repair effect on the structure of Koror Bridge, the probabilistic evaluation. The present study is based on well known and simple engineer tools: the one-dimensional beam-type was analyzed.
Keywords:Koror Bridge, Collapse, Causes, Cantilevers, Continuous Girder, Prestressed Concrete, State of Stress, Deflection, Stiffness Reduction, Probabilistic Evaluation

1. Introduction
The target of the work is to establish main causes, in the author conception, of the Koror Bridge collapse (Figure 1).
The analysis is based on the data offered by sources published, around and after 2008 when the collapse investigation was made available [1] -[4] . The most complete work is “The story of the Koror Bridge” by ManChung Tang, in which he said “Learning from our mistakes is especially useful, as it can teach us what can be done and what cannot be done. But, for the past to be useful, we must carefully and honestly present the facto”.
The engineering community often considers the study of such major collapse as an opportunity to correct and improve on future design, as T. Galambos noted [5] .
On the other hand, Prof. Bazant introduced a resolution to the Structural Engineers World Congress (Bangalore, Nov. 6, 2007), in which he pointed “the structural engineers believe that the release of all technical data

Figure 1. The Koror Bridge collapse.
would likely lead to progress in structural engineering and possibly prevent further collapses of large concrete structures” [3] .
The analysis started from the questions raised after the collapse, noted by M.-C. Tang [1] : Why was deflection so much larger than that anticipated? What would happen if there were no repairs? What did the repair change in the structure? Why did the slab of the Babeldaob cantilever near the main pier crushed and initiate the collapse? There are, too, additional problems concerning the Koror Bridge collapse: the structure system with two cantilevers for the bridge; the class of concrete used; the arrangement of tendons in the top slab near main pier; the character of partial prestressed elements of the two cantilever beams.
The present work focused on such questions and the answers are based on well known and simple engineer tools. The one-dimensional beam-type analysis was used, even it was considered to lead to great errors in deflection as well as prestress loss [3] . The results of the analysis are very close to experimental measurements. The original aspects of the present study are: a proper model for the deflections at mid-span of the bridge, the state of stress in elastic and post elastic stage for some phases of behaviour, the stage of cracked of the top of cantilever beams, the repair effect on the structure of Koror Bridge, the probabilistic evaluation.
2. The Deflection
The mid-span total deflection was a subject debated by many authors.
In the Table 1 and Figure 2, deflection at mid-span under various assumption presented by Man-Chung Tang are given.
Figure 2, proposed by the author of this work, is an illustration of the deflection due to different factors (prestress, elastic behaviour, creep influence). The last column in the Table 1 is the author proposal for the total deflection at mid-span.
The assumption started from the test results (column 3): the prestress loss is 50%. Calculation of total elastic deflection assumes a reduce girder stiffness by 50% as compared whit initial design. The creep deflection was obtained from positive deflection by introduction of modified elasticity modulus E' with formula [6] :
 (1)
(1)
where: E—elasticity modulus (Young modulus);
 (2)
(2)
qd—sustained loads and q—total loads
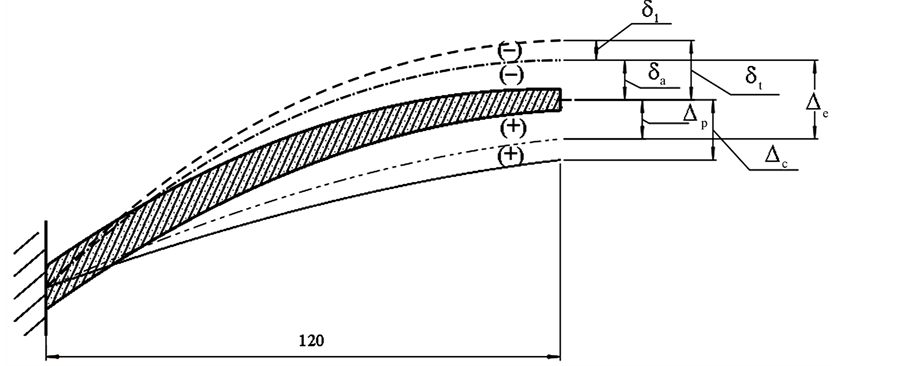
Figure 2. Deflections due to different factors.
Table 1. Deflections at mid-span of the bridge.
Notes: *− 50% stiffness reduction; ** − E' = 0.48 × E.
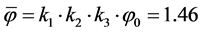 , (3)
, (3)
where:
 is the creep coefficient (
is the creep coefficient (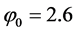 for C32/40);
for C32/40);
k1 = 0.5 represents the influence of concrete age (t > 180 days);
k2 = 1.6 is the influence of the stress in concrete (2fc/fcm);
k3= 0.7 is the influence of the relative humidity (RH = 90%).
The final deflection, taking into account creep deflection before closure (assumed 20% [1] ), is about 2.43 m. It is the same with the extrapolation of measured deflection at 36,500 days (100 years), of Δexp = 2.4 m [1] .
On the other hand, for the ultimate limit states, which may require consideration which include, among others, “excessive deformation”, is stipulated a maximum deflection as:
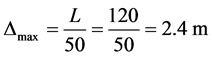 for a prestressed cantilever element;
for a prestressed cantilever element;
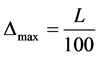 for simple supported prestressed beams;
for simple supported prestressed beams;
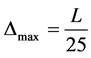 for a RC cantilever element; (4)
for a RC cantilever element; (4)
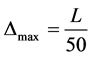 for a RC simple supported beamwhere L is the span of the element.
for a RC simple supported beamwhere L is the span of the element.
It can be seen a good correlation between the three values: calculated deflection, extrapolation of measured deflection and excessive deflection. In such circumstances there is possible to have a mean service life of 100 years (1977-2077); by probabilistic evaluation, the fractiles are 67.1 years and 133 years, where cv = 20%.
By application of the before assumption formula (1), to the initial design, the final deflection after correction will results as 6167 mm which is larger than anticipated, but is still smaller than measured deflection.
Data from Table 1 demonstrated that the main factor of the larger deflection than anticipated is prestress loss which acts with two parameters: diminishes of the counter-deflection and stiffness reduction. In such circumstances, the analysis of the contribution of the creep and shrinkage on the Koror Bridge deflection as main factors of influence are of scientific interesting but not useful for judgment of Koror Bridge behaviour. The creep and shrinkage are still not fully elucidated theories but for practical analysis of the concrete structures (including deflections) the data offered by actual norms and models are today good enough. The results presented in Table 1 are not confirmed by the statement as “The one-dimensional beam-type analysis leads to great errors in deflections as well as prestress loss” [3] . A similar conclusion for stresses, with data presented in Table 1 was found in [2] “… there are small changes in the stresses from those predicted by simple beam theory as compared whit a three-dimensional finite element built using 20-node brick elements”.
3. State of Stress
Explanation of the collapse in the slab cantilever near the main pier by concrete crushed was possible by analysis of the stress distribution. This paper has the focus of attention the stress in compression zone of the main cross-section near the pier because the collapse was initiated in these two zones of the bridge; the tension zone is more safety (see point 5). For the analysis, the critical cross-section near the main pier was taken into account (Figure 3) [3] . The analyzed phases were—the initial phase, the phase with prestress loss, the rehabilitated phase and the final phase before collapse.
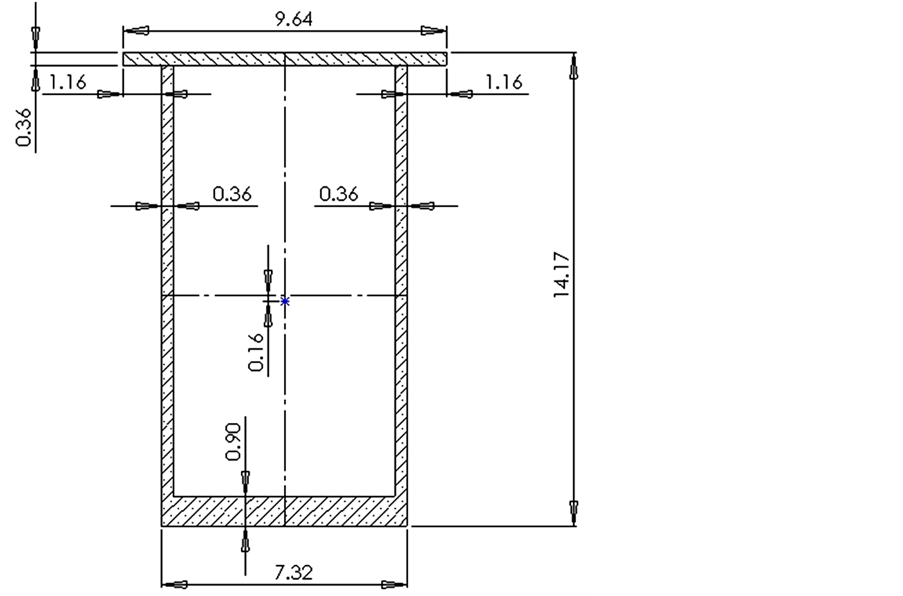
Figure 3. Cross-section near the main pier.
Under ultimate conditions the bending moment due to permanent loading and the total shear force were appreciated as actual bending moment Mg = 1800 MN·m and the shear force as Vg = 34 MN; the mean cylinder strength was found fcm = 35 MPa [1] .
The prestressing system consists of 300 tendons with the diameter of a bar, ø = 32 mm and the ultimate strength of fu = 1050 MPa. Maximum allowable stress of the tendons during stressing was 0.8fu and 0.7fu after anchoring and before losses the ultimate tension capacity of all 300 bar tendons in the top slab was: 241 MN for fu , 200 MN for 0.8fu , 180 MN for 0.7fu and 100 MN for 0.4fu [1] .
The initial phase with full prestress (0.8fu) is presented in Figure 4, where the external actions are: bending moments due to permanent loading; the prestress force P0 = 200 MN and shear forces.
The cross-section has maximum values at the bottom slab fc = –15 MPa. At the top of slab there compression stress of –5.5 MPa for the actual bending moment.
The shear is also presented in Figure 4, with the maximum value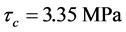 ; main tension stresses for τ= 3.35 MPa resulting are:
; main tension stresses for τ= 3.35 MPa resulting are: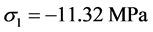 ,
, 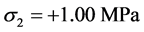 and no inclined cracks will appear.
and no inclined cracks will appear.
The phase with prestress loss of 50% (0.4fu), as it was measured by experimental determinations, is illustrated in Figure 5.

Figure 4. Elastic analysis of initial phase with full prestress.
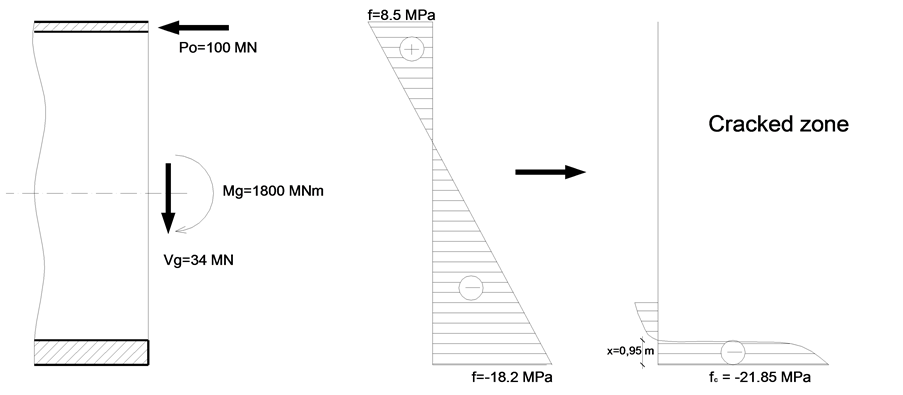
Figure 5. The phase with prestress loss.
The cause of such prestress loss was, maybe, as it was pointed in [2] “… the top flange and the web to have been particularly congested with longitudinal, transverse and vertical prestressing tendons crossing one another as well as anchorages for the various tendons”. In addition to it the top flange was cracked from the early stage of using of the bridge.
The state of stress obtained with the entire cross-section gives a tension zone at the top of the slab with a values fc = 8.5 MPa. In such circumstances, the beam will crack and state of stress of the cross-section near the centerline pier is also illustrated in Figure 5. For this phase, the inclined cracks are not imminent to appear because of small value of main stress 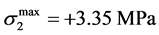 and the strength to inclined main stress is
and the strength to inclined main stress is  The pattern of cracks (with vertical crack near the main pier) is a confirmation of the diagrams illustrated in Figure 5 and data concerning stresses from Table2
The pattern of cracks (with vertical crack near the main pier) is a confirmation of the diagrams illustrated in Figure 5 and data concerning stresses from Table2
The compressed zone is restricted on 0.95 m (bottom portion of box girder) and the stresses are high: fc = 21.85 MPa.
The quality of concrete was of inferior class, even in practice of that period it was obtained as a good concrete.
The potential value of stress at the top of cross-section for different prestress forces applied at the top slab is presented in Figure 6 (from elastic analysis). It can be concluded: the cracking strength of fcr = 3.79 MPa is attended at a prestress force smaller than 200 MN (0.8fu) at 135 MN (0.56fu) for actual bending moment; a cracked zone in the early phase with smaller prestress is presented.
4. The Repair
The repair changed the bridge into continuous girder by jacking force (27 MN) at the hinge and by applied external tendons inside the box girder (34.7 MN); total force Pr = 61.7 MN (Table 2).
The actions of jacking force and external tendons have two effects:
1) A diminution of the stress on the bottom slab of critical cross-section (a reduce girder area by 50% was assumed) with about 30% which means a “discharge” of the cantilever beams. The stress on the compression zone would be fc = −15.15 MPa, Table 2 (line No.1).
2) Change the bridge from two cantilever elements into continuous girder which are acted by 30% of permanent loading, some variable vertical loads and corresponding (30%) of prestressing force (Table 2). The forces acting on cross-section are: P0 = 30.0 MN, Mg = 21.6 MNm, Vg = 12.0 MN and H = 26.7 MN. The state of stress of this phase, as well as final stress in the critical cross-section for continuous structure, are presented in

Figure 6. The correlation of potential tension stress v. prestress force at the top slab.
Table 2. The stresses for different phases.
Table 2 (line No.2).
As it was presented some horizontal forces are presented and have to act on the main and secondary piers: the thrust of bridge arch (arch effect) of H = 26.7 MN (Table 2); jacking force of 27 MN.
The result of such forces is the moving of two parts of bridge and transformation of continuous girder in the initial status. The settlement of the two bridge parts was produced in time (maybe 2 - 3 months) and only few millimeters of moving in horizontal direction will disturb the continuity of the girder at the hinge.
A similar conclusion was presented in [2] “… the new continuity joint will open up at the bottom because there was nothing to resist to tension. This would have restored the structure to its original configuration of two independent cantilevers”.
This fact will change the state of stress as it is presented in Table 2 (line No.3). The maximum compression stress is 25 MPa for the actual bending moment; no prestress force P0 was taken into account.
The repair provides a balanced state of stress but the measures were insufficient; a system to keep together the slab decks at the hinge, have been necessary.
5. Probabilistic Evaluation
The collapse evaluation of the Koror Bridge is based on the theory of structural reliability where the variables involved are considered to be random. Safety is expressed in terms of the Probability of Failure, Pf, instead of the safety factor typical of a deterministic evaluation.
Statistical definition of the variables the resistance material and of the action effects were considered with the same values and distribution as:
-coefficient of variation: ;
;
-type of distribution: Normal;
-fractiles (characteristic values) for a probability of 5%.
The high value of the coefficient of variation was taken due to many problems which had characterized the bridge: concrete class, prestressed loss, presence of cracks, large deflections etc. The representative values of the stresses are presented in Table3
Table 3 shows the main results obtained on the compressed stress of the concrete and the tensile stress of the reinforcement (bar tendons) on the critical cross-section of the bridge by using probabilistic evaluation. From deterministic evaluation there is a safety behaviour, even the global safety factor c0 is slightly superior to 1.
According to probabilistic evaluation [7] , the characteristic values of stress for action are greater as compared with the characteristic resistances. In the some time the failure probability is a very small one. From data presented there is clear to noted the reduced value of the failure probability. From the three phases of analysis, the bridge with two cantilevers, as original configuration, has a high probability of failure and the Koror Bridge is included into 15 structures which have to collapse. Failure probability of the concrete in the compressed zone of continuous girder, as well as the 300 bar tendons in the tension zone, have had a high probability of failure but smaller than for the two cantilever elements.
Table 3. Probabilistic evaluation of the failure probability.
6. Conclusions
Some very important conclusions on the causes of the Koror Bridge collapse are underlined:
1) The structure with two cantilever elements is very sensitive and vulnerable; no possibility of redistribution of the efforts; a safety coefficient depending on few parameters.
2) The cantilever elements of the Koror Bridge were partial prestressed; the part near the main pier were early cracked.
3) The quality of concrete was of interior class for a prestressed concrete element.
4) The main factor of the larger deflection than that anticipated was the prestressed loss and the cracking of concrete at the top of cross-section.
5) The arrangement of tendons in the cracked top slab near main pier was with negative influence on the prestress loss.
6) If there were not repair, the bridge could be, probably, in service for 100 years.
7) The repair of the bridge was a good idea but the measures to provide the collapse were insufficient; using a system to keep together the two parts of bridge has been necessary.
Two very important aspects are to be pointed out: the prestress loss of 50%, which was found from experimental measurements, and cracked top slab were the main factors of the large deflection; the horizontal settlement of the repaired bridge was the cause of concrete crushed near the main pier.
The analysis presented in this work is the author’s assumption on the causes of Koror Bridge collapse based on the data offered by literature. Some differences between the actual values and those used in analysis have no major influence on proposed conclusions.
References
- Tang, M.-C. (2014) The Story of the Koror Bridge. Draft for SED 14.
- Burgoyone, C. and Scantlebury, R. (2006) Why Did Palace Bridge Collapse. The Structural Engineer, 30-37.
- Bazant, Z.P., et al. (2010) Excessive Deflections of Record—Span Prestressed Box Girder. ACI Concrete International, 32, 44-52.
- Klein, G. (2008) Collapse of the Koror-Babeldaob Bridge. 17th Congress of IABSE, Chicago, Report, 98-99.
- Khal, N. (2009) Learning from Failures. Environmental, Safety and Sustainability. OEC, 1-6.
- STAS 10107/0-90 (1990) Design and Detailing of Concrete. Reinforced Concrete and Prestressed Concrete Structural Members, Bucuresti.
- Borges, J.F. and Castanheta, M. (1974) The Safety of Structures. Editura Tehnica, Bucuresti. (in Romanian)


