Open Journal of Marine Science
Vol.05 No.01(2015), Article ID:53014,9 pages
10.4236/ojms.2015.51005
Relationship between Sea Surface Single Carrier Waves and Decreasing Pressures of Atmosphere Lower Boundary
Daika Augustin, Mbane Biouele César*
Laboratory of Earth’s Atmosphere Physics, Department of Physics, University of Yaoundé I, Yaoundé, Cameroun
Email: *cesar.mbane@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2014; revised 28 October 2014; accepted 8 November 2014
ABSTRACT
Descriptions of unusually high waves appearing on the sea surface for a short time (freak, rogue or killer waves) have been considered as a part of marine folklore for a long time. A number of in- strumental registrations have appeared recently making the community to pay more attention to this problem and to reconsider known observations of freak waves. To allow a better under- standing of the behavior of rogue waves associated with tornadoes in terms of their origin, the nonlinear theory of off-balance systems is developed in the specific case of strong agitations con- stantly seen on the surface of extensive and deep rivers, when they are crossed by an atmos- phere’s low pressure system (tornadoes, cyclones, hurricanes, etc.). A mathematical model based on the Navier-Stokes and Euler Lagrange equations coupled with assumptions derived from in- strumental registrations on the training locations (or birth places) of freak waves is developed to enhance the physics of processes responsible for the formation (or origin) of the waves associated with atmosphere’s low pressure systems. Freak waves births’ constraints are mainly the need for both consistent water (i.e., extensive-deep rivers) and potential velocity flow availabilities. Nu- merical simulations, based on the use of the NLSE (Nonlinear Schrödinger Equation) are performed to validate our mathematical model on the births of single carrier waves associated with atmos- phere’s low pressure systems.
Keywords:
Nonlinear Theory of Off-Balance Systems, Births of Single Carrier Waves Associated with Atmosphere’s Low Pressure Systems, NLSE (Nonlinear Schrodinger Equation)

1. Introduction
The existence of rogue waves is now universally recognized [1] - [21] and many images on the extent of damage caused by these monsters of the ocean are available. However, the physics of processes responsible for the formation (or origin) and propagation of these phenomena as well as their prediction is not completely understood. Contrary to developed country researchers’ opinion, physics of spectacular phenomenon like rogue waves is not easily obtainable by the only use of advance data provided by high technology equipment like: Powerful Computers; sophisticated WIS (Weather Information Systems); Wind’s Profilers; Radar Drones; Lidar Drones; Satellites, etc. Indeed, rogue waves are a combination of multi-spectral processes that occur under the thermodynamic and dynamic accuracy conditions. Mathematical models [22] -[25] offer more tremendous opportunities for understanding of the systems whose physics is, at the present level of our knowledge, difficult to obtain. To allow a better understanding of the behavior of rogue waves triggered by tornadoes in terms of their origin and spatio- temporal evolution, that is, their motion and also in terms of mechanical transformations that these systems may suffer in their dealings with other systems, the nonlinear physics of off-balance systems is developed in the specific case of strong agitations constantly seen on the surface of extensive and deep rivers, when they are crossed by an atmosphere’s low pressure system (tornadoes, cyclones, hurricanes, etc.). A mathematical model based on Navier-Stokes and Euler Lagrange equations coupled with assumptions derived from the literature on the nature of the training locations (or birth places) of rogue waves is developed to enhance the physics of processes responsible for the formation (or origin) of the waves associated with atmosphere’s low pressure systems. Indeed, Navier-Stokes and Euler Lagrange equations provide evidence that waves may form on the surface of water as a reaction to impact of the decreasing pressures of the atmosphere lower boundary. It is precisely in this case, the materialization of action triggers reaction Physics’ Principle and then of a manifestation among many others of the evidence of Atmosphere-Oceans coupling. The rogue waves births’ constraints are mainly the need for both consistent water (i.e., extensive-deep rivers) and potential velocity flow domain. Numerical simulations, based on the use of the NLSE (nonlinear Schrödinger equation) on amplitude and phase modulations are performed to validate our mathematical model on the births of rogue waves associated with atmosphere’s low pres- sure systems.
2. Kinematics’ Constraints Associated with Births of Tornadoes’ (or Cyclones’) Rogue Waves
The general fluid continuity equation is given by:
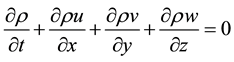 (1)
(1)
This leads to the continuity equation for an incompressible fluid
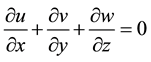 (2)
(2)
The kinematic boundary conditions
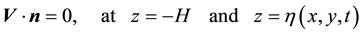 (3)
(3)
where
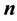 is the unit vector normal to the boundary surfaces and
is the unit vector normal to the boundary surfaces and
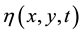 is the sea surface elevation. Hence:
is the sea surface elevation. Hence:
 (4)
(4)
Equation of motion in natural coordinates
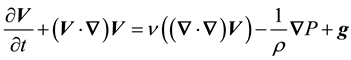 (5)
(5)
For an inviscid fluid, Equation (5) is simplify to
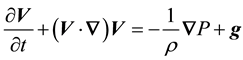 (6)
(6)
When the flow is irrotational, one can write
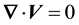 (7)
(7)
The related velocity potential is so given by
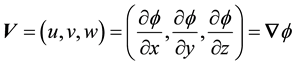 (8)
(8)
The continuity equation in regard to irrotational flow
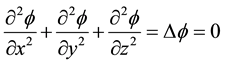 (9)
(9)
The kinematic boundary condition at the bottom of irrotational flow
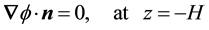 (10)
(10)
The kinematic boundary condition at the surface of the same flow
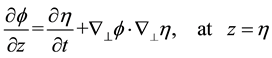 (11)
(11)
Integrating Equation (6) with respect to , leads to Bernoulli equation. Arbitrary functions of integration
, leads to Bernoulli equation. Arbitrary functions of integration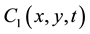 ,
,
 ,
,


potential, yielding exactly the same flow

where,


Due to the smallest-vertical extend of oceans with regard to earth’s radius, we can consider


When atmosphere’s low pressure systems (LOW on Figure 1) cross the ocean: The atmosphere low boundary decreasing pressures field above the ocean replaces

Figure 1. LOW (low pressure systems) and HIGH (higher pressure system) on a mean sea-level pressure (millibars) map.
And then, taking



Formula (13) is our mathematical model on the occurrence of oceans’ surface single carrier waves associated with atmosphere’s low pressure systems (i.e., the mainly origin of tornadoes; cyclones or hurricanes related waves).
-

-

-


According to Formula (13), the height of single carrier waves depends mainly on low pressure deepest. i.e.,
3. Implementation of NLSE
According to the nonlinear Schrödinger equation (NLSE), the combination of unstable waves can trigger a sin- gle wave which can reach up to three or five times the amplitude of the single carrier waves (that is, the wave energy is basically concentrated in a single wave number). Let’s consider a surface wave whose main compo-
nent



We consider the case of energy concentrated mainly around two-wave numbers

where A and B satisfy the Coupled Nonlinear Schrödinger Equations [22] :


Here, we took into account that the energy distribution is almost monochromatic and the Taylor expansion of the pulse around the two wave numbers.
If the energy concentrated mainly around a wave number, the evolution of a waveform produced by a group unstable wave only on the nonlinear Schrodinger equation is:

Putting the previous relation (18) under the dimensionless form, we obtain the nonlinear Schrödinger equation rewrites in the form [23] [24] :

This is an integrable equation. We can find solution which form is:

where







Figure 2. (a) Barograph Trace showing the passage of an immature hurricane at low latitude. The sea-level pressure drops from reference index_30 to index_28.50; (b) Barograph Trace accompanying the passage of a small, intense hurricane. The sea- level pressure drops from reference index_30 to index_28.00; (c) Barograph Trace indicating the passage of a mature hurricane. The ground surface pressure drops from reference index_30 to index_27.30; (d) One of the deepest barometer readings for the entire world. The ground surface pressure drops from reference index_30 to index_27.00, Hurricane “Janet”_Ghetumal (Mexico) Barograph Trace.
Substitution of (20) in (19), gives (21):

We are interested in a homoclinic orbit to the fixed point and we obtain finally the solution (22):


Below is an exact analytical solution of Equation (19):

with


Relation (24) can reach to a family of spatiotemporal solutions of breather type with the advantage that they describe the plane wave. The rational solitons’ family can be transform to Peregrine breather type of solution:

4. Results and Discussion
According to scientists’ common opinion, questions raised by observations lead to physics’ laws while observations can in no way serve as physics’ laws. Indeed, advance equipment like powerful computer; sophisticated WIS (Weather Information Systems); Wind’s Profilers; Radar Drones; Lidar Drones; Satellites, etc., cannot completely solve problems regarding the adverse effects of climate change without the contributions of performing mathematical models on physics of processes responsible of that climate change. Earth’s ecosystem is considerably modified by adverse effects of climate change and this irreversible process reveals human beans vulnerability vis-à-vis of phenomenon like rogue waves; landslides; coastal cities floods, etc. Geometries of sea surface carrier waves associated with atmosphere low pressure systems are drawn on Figures 3(a)-(c) and Figure 4. Taking into account the Barograph Traces, one can see that the atmosphere low pressure systems can take more than two days to cross a Weather Station. Barograph traces also show that the deepest of impacts on sea- level pressure depends on many weather’s parameters. Figures 3(a)-(c) represent carrier-waves for different wave numbers. Single carrier waves Interferences (or combinations) are shown on Figure 4. The resulting wave (Figure 4) reveals that Interferences are mainly constructive in the case of sea-surface carrier waves. On Figure 5(a) and Figure 5(b), one can see lands’ and oceans’ tornadoes respectively. Overland Tornadoes are daily phe- nomena (Figure 5(a)) which occur only during sunny days due to additional greenhouse effects [26] [27] . The same thermodynamics’ process occurs over oceans even by night (Figure 5(b)) and in this case, it escapes to vi- gilance of weather alert instruments and represents a higher risk for airline pilots as well as seamen’s. This is, according to Mbane’s previous publications [26] -[28] , the main reason why many planes have disappeared when crossing oceans by night. There is convincing evidence that Air France and Malaysian Airlines planes are recent victims of nightly oceans’ tornadoes epiphenomenon.
5. Conclusion
Many avenues of scientific research (including ours) are now open to better understand the physics, structure, composition and functioning of atmosphere lower pressure systems and their impacts on oceans, mainly in the case of rogue waves’ implementation. Indeed, Earth’s atmosphere is in contact with the oceans, oceans affect it, but in return it acts upon them: We speak of oceans-atmosphere coupling. To study the physics of rogue waves associated by tornadoes (cyclones or hurricanes) in terms of their origin, the nonlinear physics of off-balance systems has been developed in the specific case of strong agitations constantly seen on the surface of extensive and deep rivers, when these rivers are crossed by an atmosphere’s low pressure system. Euler-Lagrange and



Figures 3.(a)-(c) Simulations of geometry of ocean surface single carrier waves associated with atmosphere’s low pressure systems for different wave numbers ((a) K0 = 1; (b) K0 = 2 and (c) K0 = 4.0).
Figure 4. Simulations of geometry of oceans’ surface multispectral carrier wave associated with atmosphere low pressure systems shown on Figure 5(b).

Figure 5. (a)-(b) Tornadoes 3D-profiles ((a), above the land; (b), above the ocean). One may note that: Tornadoes can occur even by night on the Oceans (b) and represent in this case a higher risk for aircrafts. This thermodynamics’ process is impossible by night on the Land (due to land’s thermal inertia).
Navier-Stokes equations have provide evidence that waves may form on the surface of water as a reaction to impacts of sea-level decreasing pressures of the atmosphere lower boundary. That is precisely the materializa- tion of action triggers reaction Physics’ Principle and then of a manifestation among many others of the convinc- ing evidence of Atmosphere-Oceans coupling. A mathematical model based on the Navier-Stokes equations coupled with assumptions derived from advance data bases on rogue waves has been developed to allow a better understanding of processes responsible for the formation (or origin) of sea surface waves. The rogue waves births’ constraints are mainly the need for availability of both consistent water (i.e., extensive-deep rivers) and potential velocity flow. Numerical simulations, based on NLSE (nonlinear Schrödinger equation) on amplitude and phase modulations has been successfully performed to validate our relationship between sea-surface strong agitations and decreasing pressure of atmosphere lower boundary.
References
- Touboul, J., Kharif, C., Pelinovsky, E. and Giovanangeli, J.P. (2008) On the Interaction of Wind and Steep Gravity Wave Groups Using Miles’ and Jeffreys’ Mechanisms. Nonlinear Processes in Geophysics, 15, 1023-1031. http://dx.doi.org/10.5194/npg-15-1023-2008
- Benjamin, T.B. (1967) Instability of Periodic Wave Trains in Nonlinear Dispersive Systems. Proceedings of the Royal Society of London, 299, 59-75. http://dx.doi.org/10.1098/rspa.1967.0123
- Karsten, T. and Igor, K. (2000) On Weakly Nonlinear Modulation of Waves on Deep Water. Physics of Fluids, 12, 24-32.
- Onorato, M., Osborne, A.R., Serio, M., Cavaleri, L. and Stanberg, T.C. (2004) Observation of Strongly Non-Gaussian Statistics for Random Sea Surface Gravity Waves in Wave Flume. Physical Review E, 70, Article ID: 067302. http://dx.doi.org/10.1103/PhysRevE.70.067302
- Socquet, H., Juglar, A., Dysthge, K., Trulsen, K., Krogstad, H.E. and Liu, J. (2005) Probability Distributions of Surface Waves during Spectral Change. Journal of Fluid Mechanics, 542, 195-216. http://dx.doi.org/10.1017/S0022112005006312
- Dyachenko, A.L. and Zakharov, V.E. (2005) Modulation Instability of Stokes Wave-Freak Wave. Journal of Experimental and Theoretical Physics, 81, 318-322.
- Kharif, C. and Pelinovsky, E. (2003) Physical Mechanism of the Rogue Wave Phenomenon. European Journal of Mechanics/B-Fluid, 22, 603-634.
- Wu, C.H. and Yao, A. (2004) Laboratory Measurements of Limiting Freak Waves on Current. Journal of Geophysical Research, 109, 1-18. http://dx.doi.org/10.1029/2004JC002612
- White, B.S. and Fomberg, B. (1998) On the Chance of Freak Waves at Sea. Journal of Fluid Mechanics, 355, 113-138. http://dx.doi.org/10.1017/S0022112097007751
- Zakharov, V.E. and Kharitonov, N.G. (1970) Instability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. Journal of Applied Mechanics and Technical Physics, 11, 747-751. http://dx.doi.org/10.1007/BF00851899
- Shener, L. (2010) On Benjamin-Feir Instability and Evolution of Nonlinear Wave with Finite-Amplitude Side Bands. Natural Hazards and Earth System Sciences, 10, 2421-2427. http://dx.doi.org/10.5194/nhess-10-2421-2010
- Leblanc, S. (2008) Wind Forced Modulations of Finite Depth Gravity Waves. Physics of Fluids, 20, Article ID: 116603. http://dx.doi.org/10.1063/1.3026551
- Batra, K., Sharma, R.P. and Verga, A.D. (2006) Stability Analysis on Nonlinear Evolution Patterns of Modulational Instability and Chaos Using One-Dimensional Zakharov Equations. Journal of Plasma Physics, 72, 671-686. http://dx.doi.org/10.1017/S002237780500423X
- Banner, M.I. and Song, J.B. (2002) On Determining the Onset and Strength of Breaking for Deep Water Waves. Part II: Influence of Wind Forcing and Surface Shear. Journal of Physical Oceanography, 32, 2559-2570. http://dx.doi.org/10.1175/1520-0485-32.9.2559
- Brown, M.G. and Jensen, A. (2001) Experiments on Focusing Unidirectional Water Waves. Journal of Geophysical Research, 106, 16917-16928. http://dx.doi.org/10.1029/2000JC000584
- Jeffreys, H. (1925) On the Formation of Wave by Wind. Proceedings of the Royal Society A, 107, 189-206. http://dx.doi.org/10.1098/rspa.1925.0015
- Philips, O.M. (1957) On the Generation of Waves by Turbulent Wind. Journal of Fluid Mechanics, 2, 417-455. http://dx.doi.org/10.1017/S0022112057000233
- Makin, V.K., Branger, H., Peirson, W.L. and Giovanangeli, J.P. (2007) Stress above Wind-Plus-Paddle Waves: Modeling of a Laboratory Experiment. Journal of Physical Oceanography, 37, 2824-2837. http://dx.doi.org/10.1175/2007JPO3550.1
- Shemer, L., Goulitski, K. and Kit, E. (2007) Evolution of Wide Spectrum Unidirectional Wave Groups in a Tank: An Experimental and Numerical Study. European Journal of Mechanics―B/Fluids, 26, 193-219. http://dx.doi.org/10.1016/j.euromechflu.2006.06.004
- Song, J.B. and Banner, M.I. (2002) On Determining the Onset and Strength of Breaking for Deep Water Waves, Part I: Unforced Irrotational Wave Groups. Journal of Physical Oceanography, 32, 2541-2558. http://dx.doi.org/10.1175/1520-0485-32.9.2541
- Stanton, T., Marshall, D. and Houghton, R. (1932) The Growth of Waves on Water Due to the Action of the Wind. Proceedings of the Royal Society A, 137, 283-293. http://dx.doi.org/10.1098/rspa.1932.0136
- Daika, A., Etoundi, H.M., Ngabireng, C.M. and Mbané-Biouélé, C. (2012) Application of Benjamin-Feir Equations to Tornadoes’ Rogue Waves Modulational Instability in Oceans. International Journal of Physical Sciences, 7, 6053-6061.
- Talon, M. (2006) Ondes de Surface. LPTHE-Université Paris VI-CNRS, France.
- Miles, J.W. (1996) Surface-Wave Generation: A Viscoelastic Model. Journal of Fluid Mechanics, 322, 131-145. http://dx.doi.org/10.1017/S002211209600273X
- Daika, A., Nkoa Nkomom, T. and Mbané Biouélé, C. (2014) Application of Stationary Phase Method to Wind Stress and Breaking Impacts on Ocean Relatively High Waves. Open Journal of Marine Sciences, 4, 18-24. http://dx.doi.org/10.4236/ojms.2014.41003
- Mbané Biouele, C. (2013) Hurricanes and Cyclones Kinematics and Thermodynamics Based on Clausius-Clapeyron Relation Derived in 1832. International Journal of Physical Sciences, 8, 1284-1290. http://www.qcqdemicjournals.org/IJPS
- Mbané Biouele, C. (2014) Relationships between Earth’s Rotation or Revolution and Geographical Extent of the Global Surface Monsoons. Atmospheric and Climate Sciences, 4, 47-52. http://dx.doi.org/10.4236/acs.2014.41006
- Mbané Biouele, C. (2014) Application of Clausius-Clappeyron Relation (1832) and Carnot Principle (1824) to Earth’s Atmosphere Tricellular Circulation. Atmospheric and Climate Sciences, 4, 1-6. http://dx.doi.org/10.4236/acs.2014.41001
NOTES
*Corresponding author.





