Received 14 April 2016; accepted 10 June 2016; published 13 June 2016

ABSTRACT

Estimating of river discharge is one of the more important parameters in the water resources management. In recent years, due to increasing population, increased water consumption in industrial, agricultural and health sections, thus water shortge becomes a global problem. Accurate estimation of the river discharge is one of the most important parameters in surface water resources management, especially in order to determine appropriate values in flood, drought, drinking, agricultural and industral topics. The case study in this research is Mahabad River that is located in west Azarbaijan province in west north of Iran. In this study, we used 70%, 15% and 15% data in order to train, validate and test, respectively. In this study, data of Kawtar and Baitas stations were used in order to determine Mahabad River discharge. In each ststion, several different networks were prepared using NeuroSolutions V.6.0 software. The neural models included Multilayer Perceptron (MLP), Generalized Feed Forward, Jordan/Elman, Radial Basis Functions (RBF) and Principle Component Analysis (PCA), and different transfer functions included Tanh, Sigmoid, Linear Tanh, Linear Sigmoid and the number of hidden layers of.The different number of nodesin layers with different learning algorithms (Momentum, Levenberg Marquardt, Quickprop, DeltaBarDelta, Conjugate Gradient) and different networks were compared. The results showed the artificial neural networks. They predicted the river discharge with 10.67 and 0.94 (m³/s)² and the high value of correlation coefficient with 0.88 and 0.75 for Kawtar and Baitas stations respectivly.

Keywords:

Artificial Neural Networks, Discharge, Estimate, Mahabad, NeuroSolutions Software, River

1. Introduction

Estimation of river flow is a key element in water resources management. The importance of this issue is to the extent that most affairs relating to the water engineering science including the design of hydraulic structures for large water supply systems, watershed management plans and culverts, calculating the height of the walls for riverbank stabilization, rivers catchment basin, dam stilling basin design, design of dam spillways, safety of hydraulic structures and facilities, planning and managing surface waters and dams reservoirs, erosion and sediment control, design of waste water disposal network arising from rainfall in urban basins and highways, distribution and control of flooding, irrigation, drainage network management, human, urbanization, industrialization and agricultural consumption have long been in need of it. The new technique of applying artificial neural network model based on artificial intelligence is widely used in various fields of engineering, in particular, water and river engineering. Kisi (2004) [1] used artificial neural network and regression in a study on Gossau Basin located in Issaquah state of Japan to predict the monthly streamflow. The results showed higher accuracy of artificial neural networks than the regression model. Kisi (2005) [2] , acted to estimate daily and monthly streamflows of rivers Gossau in Japan, Blackwater and Gila in the United States, Flavous in Turkey using temporal patterns of neural network and compare the results with time series methods. Accordingly, he showed that Artificial Neural Network (ANN) was more accurate compared to these methods. Noori et al. (2010) [3] acted to estimate Sufi Chay River flow of Tabriz using Neural Network and regression and selected Neural Network as a model with higher accuracy. Yeh (2007) [4] used Neural Network Model and regression to estimate discharge of river and achieved satisfactory results. Comparing the results indicated the high estimation accuracy of the neural network compared to regression model.

2. Methodology

Mahabad River catchment area is located in the south of Lake Urmia in West Azerbaijan province in Iran. Area of this basin is as much as 1524.53km² that accounts for 3 percents of catchment basin area of Lake Urmia (Persian: Daryāche-ye Orūmiye). Geographically, Mahabad River catchment area is located between 45 degrees 25 minutes 9 seconds of east longitude and 36 degrees 23 minutes 51 seconds of north latitude (Figure 1). The catchment basin is almost oval-shaped with a large diameter in north-south direction and a small-diameter in the direction of East-West. The area is bordered with Small Zab Catchment in the South West, Gadar in the West and Siminehrood in South East and East and Lake Urmia in the North. The most important branches of Mahabad River are Kawtar and Baitas stations. Bitas branch is originated from the altitude over 2000 meters of Mahmudabad Village and Shakhghol Mountains and its catchment basin area is estimated as 27,900 hectares that flows into Mahabad lake dam near Mahabad City. Kawtar branch in the western area of basin originates from the height of 2350 meters in southwest of the basin, its catchment basin area is 53,700 hectares and moves to the Bengwen branch and continues to Kawtar village and flows into Mahmudabad dam.

Artificial neural network evaluation criteria (Performance Measures)

To evaluate the considered models, many quantitative indicators were used to evaluate the Artificial Neural Networks that can be calculated through the following relationships.

Various types of activation functions can be used in a neural network (e.g., linear, threshold, sigmoid). The sigmoid function is by far the most common form of activation function used in ANNs, due to its ability to describe nonlinear relationships, in this case a natural process (Nayak et al., 2006; Trichakis et al., 2011) [5] [6] .

Correlation coefficient: The size of the mean square error (MSE) can be used to determine how well the network output fits the desired output, but it doesn’t necessarily reflect whether the two sets of data move in the same direction. For instance, by simply scaling the network output, we can change the MSE without changing the directionality of the data. The correlation coefficient (r) solves this problem. By definition, the correlation coefficient between a network output x and a desired output d is:

The correlation coefficient is confined to the range [−1, 1]. When r =1 there is a perfect positive linear correlation between x and d, that is, they covary, which means that they vary by the same amount. When r = −1, there is a perfectly linear negative correlation between x and d, that is, they vary in opposite ways (when x increases, d decreases by the same amount). When r = 0 there is no correlation between x and d, i.e. the variables are called uncorrelated. Intermediate values describe partial correlations. For example, a correlation coefficient of 0.88 means that the fit of the model to the data is reasonably good (NeuroSolutions Help, lnc. 2010) [7] .

MSE: The mean squared error is simply two times the average cost. The formula for the mean squared error is:

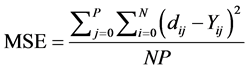
NMSE: The normalized mean squared error is defined by the following formula:

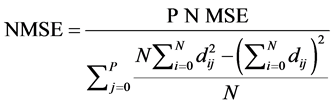
% Error: The percent error is defined by the following formula:

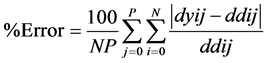
AIC: Akaike’s information criterion (AIC) is used to measure the tradeoff between training performance and network size. The goal is to minimize this term to produce a network with the best generalization:

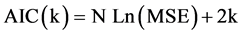
MDL: Rissanen’s minimum description length (MDL) criterion is similar to the AIC in that it tries to combine the model’s error with the number of degrees of freedom to determine the level of generalization. The goal is to minimize this term (NeuroSolutions Help, lnc., 2010) [7] :

Baitas station artificial neural networks:

In this study, after collecting information and data for Bitas Station, several different neural networks were created by NeuroSolutions software, which corresponding charts and tables of a number of them were selected for the study and drawn in this section (see Table 1 and Figures 2-6).

Kawtar station artificial neural networks:

In the following of the research, after collecting information and data for Kawtarstation, several different samples of neural network were created by NeuroSolutions software similar to Bitas station and corresponding charts and tables of some of them were selected and drawn in this section (see Table 2 and Figures 7-11).

Results

A) Using the Mean Square Error and Correlation Coefficient between actual and computational (desired)

vales, the best possible options were chosen to determine the best topology and the results have been identified in Table 3.

B) The results indicate high accuracy of artificial neural networks to discharge estimation of rivers due to the low value of the Mean Square Error with 10.67 and 0.94 (m³/s)², and the high value of the correlation coefficient to the value of 0.88 and 0.75 for Kawtarand Bitas stations respectively.

3. Discussion

The sensitivity analyze showed that the most sensitive parameters to predict river discharge were the mean temperature of last month, mean temperature of current month, the pan evaporation of last month, the precipitation

of the current month and the precipitation of the last month respectively. The results showed that the most important parameters to predict river discharge were river discharge parameters of last month and two months ago respectively. Also the results showed that the best topology to predict river discharge for Beitas and Kawtar stations was obtained with Multilayer Perceptron neural model, sigmoid function and Levenberg-Marquardt training algorithm, which was agreement with the studies carried out by previous researchers.

Cite this paper

Saman Mohammadi,Maaroof Siosemarde, (2016) Application of Artificial Neural Networks in Order to Predict Mahabad River Discharge. Open Journal of Ecology,06,427-434. doi: 10.4236/oje.2016.67040

References

NOTES

^*Corresponding author.