Advances in Biological Chemistry
Vol.3 No.1(2013), Article ID:27790,11 pages DOI:10.4236/abc.2013.31005
Theory of cold denaturation of proteins
![]()
Department of Physical Chemistry, The Hebrew University of Jerusalem, Edmond J. Safra Campus, Jerusalem
Email: arieh@fh.huji.ac.il
Received 12 November 2012; revised 19 December 2012; accepted 28 December 2012
Keywords: Protein Folding; Cold Denaturation; Hydrophobic; Hydrophilic Effects
ABSTRACT
A new approach to the problem of cold denaturation is presented. It is based on solvent-induced effects operating on hydrophilic groups along the protein. These effects are stronger than the corresponding hydrophobic effects, and they operate on the hydrophilic groups which are plentiful than hydrophobic groups. It is shown that both heat and cold denaturation can be explained by these hydrophilic effects.
1. INTRODUCTION
Understanding the Protein Folding Problem (PFP) has been one of the most challenging problems in molecular biology. An even more challenging problem is known as the cold-denaturation process [1-13].
In an excellent review article entitled “Cold Denaturation of Proteins”, Privalov makes the following comments [1]:
“…disruption of the native structure upon heating, the heat denaturation of protein, appear to be an obvious effect. By the same argument, a decrease of temperature should only induce processes leading to increasing order.”
Indeed for any process in which a molecule P converts from a state F having a lower energy and lower entropy to a state U having a higher energy and higher entropy, we should expect that as we increase the temperature the process will proceeds from F to U. When the temperature is lowered the reverse process from U to F is expected to occur. There is no mystery in this.
The mystery of protein folding upon decreasing the temperature is that the conversion from U to F occurs at a range of temperatures at which the protein should have attained the U, rather than the F state. Thus, the main challenge is to find the factors that cause the folding at relatively higher temperatures.
It is generally believed that water is the main factor that confers stability to the folded state (F) [14]. This belief is supported by the fact that the addition of a large quantity of a co-solvent at a fixed temperature, causes denaturation. This means that in the absence of a waterrich environment, the protein would have been in the unfolded state (U).
How exactly water molecules help in maintaining the stability of the folded state at temperatures which favor the unfolded state has been the essence of the mystery associated with protein folding.
In 1959, Kauzmann introduced the idea that the hydrophobic (HfO) effect is probably one of the major factors that confer stability to the native structure of the protein [14]. Since then most people held the view that the HfO effect is the dominant factor in maintaining the stability of the native structure of protein [14,15].
The dominance of the HfO effect in protein folding was challenged in the 1990s [16-18]. It was found that Kauzmann’s model for the HfO effect is not adequate in explaining the folding of proteins. Instead, a new and a rich repertoire of hydrophilic (HfI) effects were discovered. These HfI effects provided explanation for both the process of protein folding and protein-protein association. In effect, the discovery of the HfI effects has removed the mystery out of the protein folding phenomenon. This aspect of protein folding has been discussed in great detail elsewhere [15,19].
This article is devoted to the phenomenon of cold denaturation (CD) of proteins. As in the PFP, there are many factors that are operative in the process of CD. We shall examine some of these factors which, to the best of the author’s knowledge were never considered before.
The main problem of cold denaturation is the following. It is relatively easy to understand the process of denaturation as the temperature increases. This aspect of the problem is briefly discussed in Section 2. When we cool down some solutions of a denatured protein a spontaneous renaturation occurs. The mystery associated with this process is one part of the PFP, and will not be discussed here [19]. Yet, an even greater mystery lurks at lower range of temperatures. In thermodynamic terms, we write the standard Gibbs energy of folding as
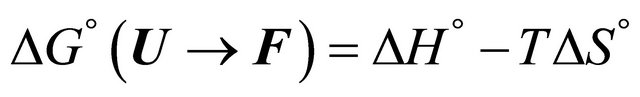 (1.1)
(1.1)
At sufficiently high temperature the entropy term will dominate. Since 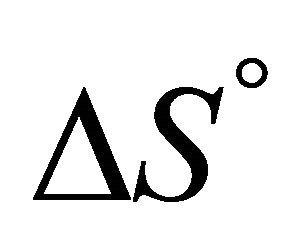 for folding is negative, the standard Gibbs energy of folding at high temperatures is positive, i.e. the U state is favored. When the temperature is lowered, there must be an energetic reason that makes
for folding is negative, the standard Gibbs energy of folding at high temperatures is positive, i.e. the U state is favored. When the temperature is lowered, there must be an energetic reason that makes  negative and large enough to over compensate for the large positive
negative and large enough to over compensate for the large positive . This is essentially the PFP, namely what makes the folded structure more stable at lower temperatures.
. This is essentially the PFP, namely what makes the folded structure more stable at lower temperatures.
Accepting whatever explanation for the change in the sign of ![]() from positive to negative upon lowering the temperature, we expect that as we further lower the temperature, the value of
from positive to negative upon lowering the temperature, we expect that as we further lower the temperature, the value of  will become smaller. Therefore, we should expect that
will become smaller. Therefore, we should expect that ![]() will become even more negative as we lower the temperature. The fact that
will become even more negative as we lower the temperature. The fact that ![]() becomes positive at lower temperature is therefore more of a mystery than the folding of the protein at higher temperature range As in the case of protein folding, most theoretical approaches to CD have been based on the HfO effects [2-13]. It is well known that both HfO solvation and HfO interaction increase, in absolute magnitude, as the temperature increases. This is true for temperature range at which the native structure of proteins is stable. Therefore, it is not a surprise that all microscopic theories of CD have been based on the HfO effects. Unfortunately, the strength of the HfO effects was grossly exaggerated in protein folding as well as in CD [15,19]. To the best of the author’s knowledge no one has considered the HfI effects in connection with the phenomenon of CD.
becomes positive at lower temperature is therefore more of a mystery than the folding of the protein at higher temperature range As in the case of protein folding, most theoretical approaches to CD have been based on the HfO effects [2-13]. It is well known that both HfO solvation and HfO interaction increase, in absolute magnitude, as the temperature increases. This is true for temperature range at which the native structure of proteins is stable. Therefore, it is not a surprise that all microscopic theories of CD have been based on the HfO effects. Unfortunately, the strength of the HfO effects was grossly exaggerated in protein folding as well as in CD [15,19]. To the best of the author’s knowledge no one has considered the HfI effects in connection with the phenomenon of CD.
In Sections 3 and 4 we show that both heat and cold denaturation can be explained by the HfI effects. The HfO effects do contribute in the right direction to the CD, but their strength is about an order of magnitude weaker than the corresponding HfI effects. Hence, we conclude that the HfI effects must play the major role in both heat and cold denaturation.
2. THE UNFOLDING OF PROTEINS AT HIGH TEMPERATURES
Consider the process of folding of a protein
 (2.1)
(2.1)
We assume that all the accessible energy levels of the protein P can be split into two groups, Figure 1. The first group denoted F is characterized by lower energies and a fewer number of states. The second group, denoted U is characterized by higher energies and very large number of states.
The internal partition function of the protein P in an ideal gas phase is split into two terms;
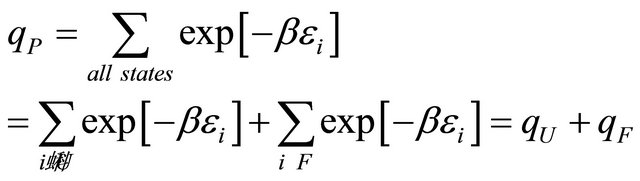 (2.2)
(2.2)

Figure 1. A schematic split of all energy levels of a molecule P in two groups; F having lower energies and fewer states, and U having higher energies and many more states.
The canonical partition function of a system of N molecules in a volume V and temperature T is
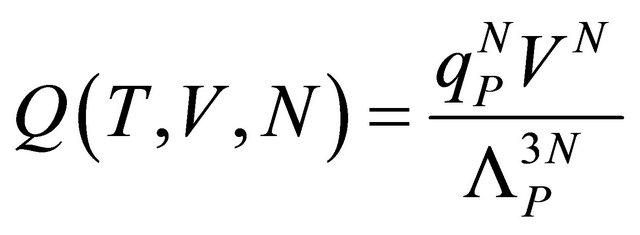 (2.3)
(2.3)
where 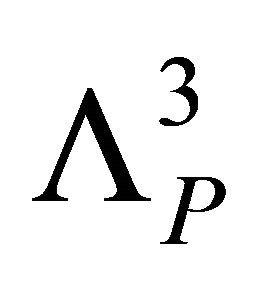 is the momentum partition function,
is the momentum partition function, 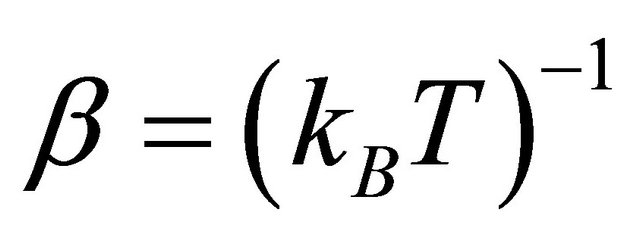 , with kB the Boltzmann constant and the T the absolute temperature.
, with kB the Boltzmann constant and the T the absolute temperature.
The equilibrium constant for the reaction (2.1) can be easily obtained by maximizing the Helmholtz energy, or equivalently by finding the most probable distribution of molecules between the two states U and F [15].
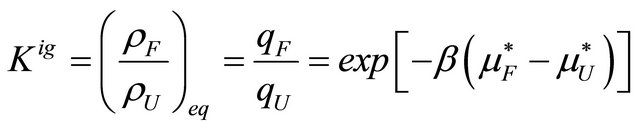 (2.4)
(2.4)
where  and
and  are the pseudo chemical potentials of F and U, respectively [20]. These are defined by
are the pseudo chemical potentials of F and U, respectively [20]. These are defined by
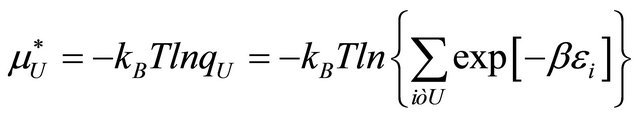 (2.5)
(2.5)
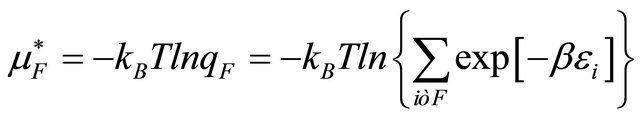 (2.6)
(2.6)
Note that since the momentum partition functions of U and F are equal to each other, the equilibrium constant depends only on the ratio of the internal partition functions of U and F.
In this system the standard Helmholtz energy, entropy and energy of the system are given by
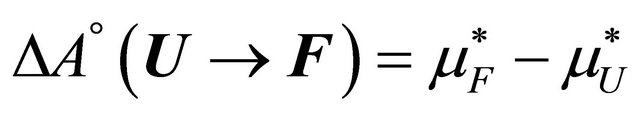 (2.7)
(2.7)
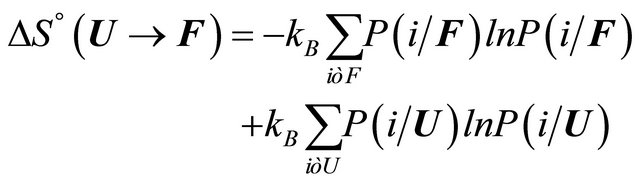 (2.8)
(2.8)
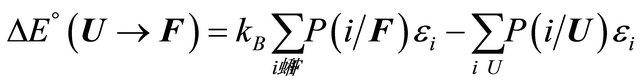 (2.9)
(2.9)
where 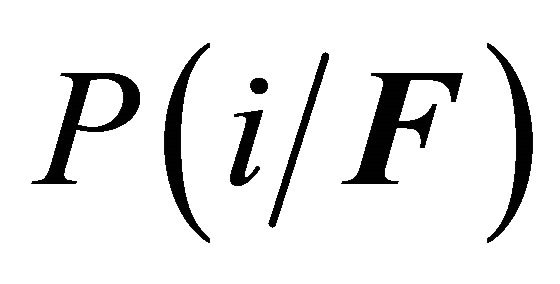 is the conditional probability of finding the molecule in state i, given that it is in the group of states F. A similar meaning applies to
is the conditional probability of finding the molecule in state i, given that it is in the group of states F. A similar meaning applies to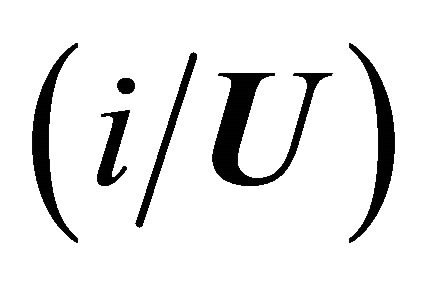 .
.
According to our assumptions 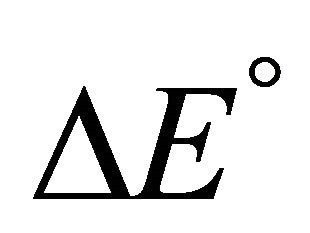 is negative, i.e. the average energy level of F is lower than that of U. Also,
is negative, i.e. the average energy level of F is lower than that of U. Also, 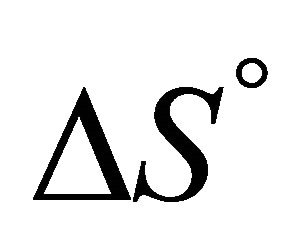 is negative for this reaction. Therefore, as the temperature increases we must have
is negative for this reaction. Therefore, as the temperature increases we must have
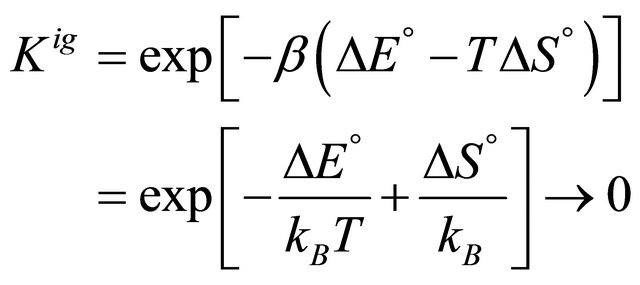 (2.10)
(2.10)
We find that as ,
,  , hence
, hence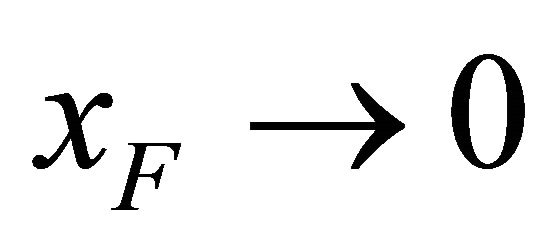 . A simple example is shown in Figure 2. Here, we have only two energy levels U and F with different degeneracies
. A simple example is shown in Figure 2. Here, we have only two energy levels U and F with different degeneracies  and
and , respectively. In this case
, respectively. In this case
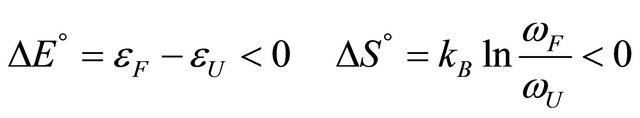 (2.11)
(2.11)
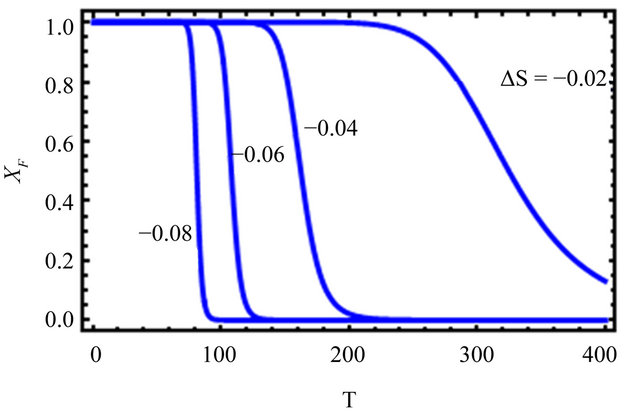

Figure 2. “Denaturation curves” for a system of two energy levels, with 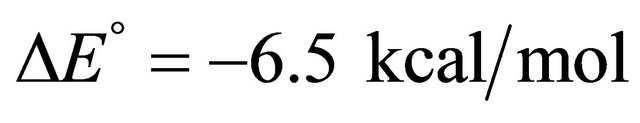 and various values of
and various values of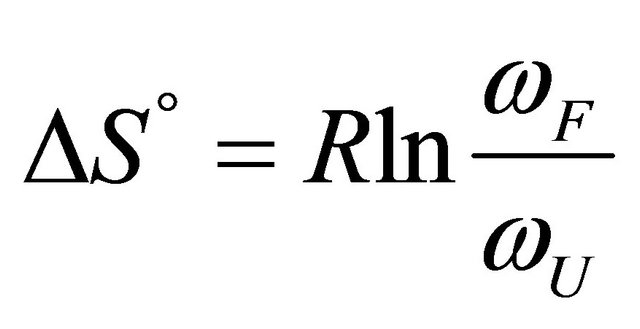 , The computations are based on Eq.2.11. These curves correspond to the degeneracy ration
, The computations are based on Eq.2.11. These curves correspond to the degeneracy ration  of about:
of about: 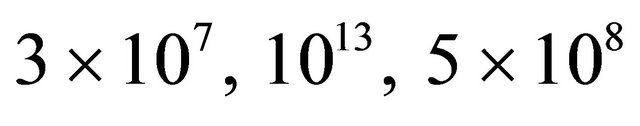 and
and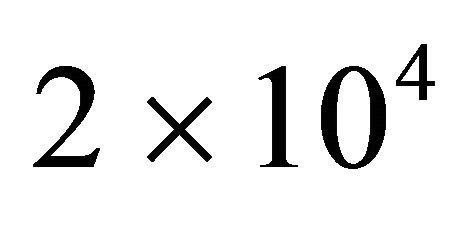 . Lower panel shows the derivatives of
. Lower panel shows the derivatives of  with respect to T.
with respect to T.
Figure 2 shows a series of “denaturation” curves as a function of temperature for a fixed energy difference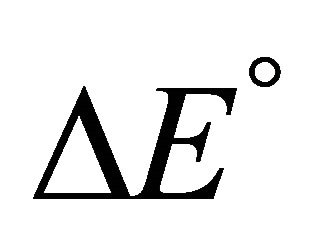 , and varying the ratio of the degeneracies
, and varying the ratio of the degeneracies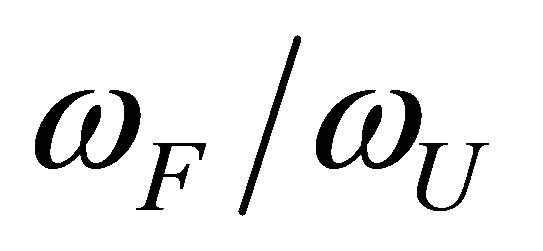 , or
, or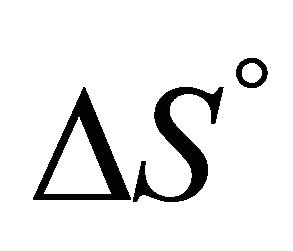 .
.
We see that as we increase the ratio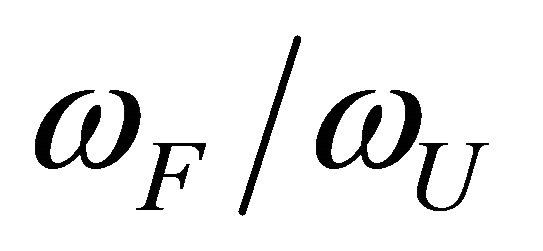 , the transition from F to U become sharper and occur at lower temperatures. The reason is simple and well understood. At higher temperatures the molecule will favor the state of higher degeneracy. On the other hand, at very low temperatures the molecule will favor the state of lower energy. The reason for the transition from F to U in real protein is essentially the same as in the simple case discussed above.
, the transition from F to U become sharper and occur at lower temperatures. The reason is simple and well understood. At higher temperatures the molecule will favor the state of higher degeneracy. On the other hand, at very low temperatures the molecule will favor the state of lower energy. The reason for the transition from F to U in real protein is essentially the same as in the simple case discussed above.
3. THE FIRST MYSTERY: WHY PROTEINS FOLD AS WE LOWER THE TEMPERATURE
We have seen that for any polymer having two macrostates; one having lower average energy and low degeneracy denoted F, and the second having higher average energy and higher degeneracy denoted U, we expect that as , the system will favor F, whereas as
, the system will favor F, whereas as , the system will favor U.
, the system will favor U.
Now suppose that the molecular parameters are such that at about room temperature, say . We find that
. We find that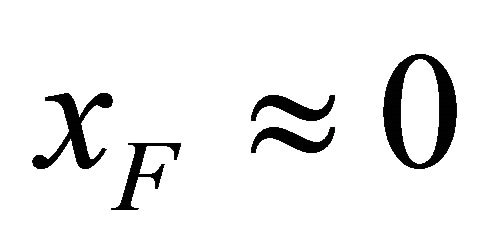 . For instance, if the ratio of the degeneracies is
. For instance, if the ratio of the degeneracies is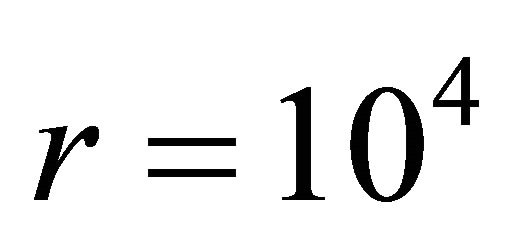 , and the energy difference between the two states is of the order of
, and the energy difference between the two states is of the order of 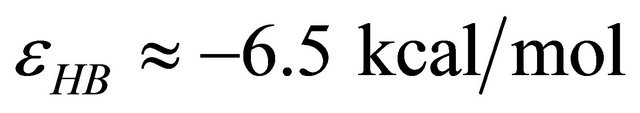 we find that at
we find that at 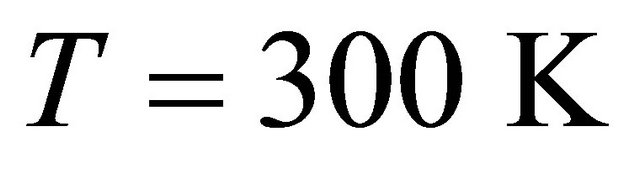 nearly all the molecules will be in the U state (see right curve in Figure 2). In this system one must go to temperatures below freezing
nearly all the molecules will be in the U state (see right curve in Figure 2). In this system one must go to temperatures below freezing 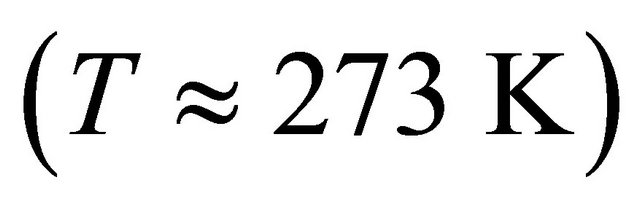 to find any significant concentration of F.
to find any significant concentration of F.
Now, we place the same polymer in water, and for simplicity we assume that the solution is very dilute with respect to the polymer. In this solution, if we find that the majority of the polymer molecules are now in the F state, then we must conclude that the equilibrium constant has changed, due to solvation effects. We write the equilibrium constant in the liquid state as [20]
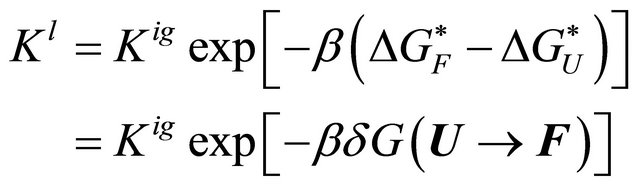 (3.1)
(3.1)
where 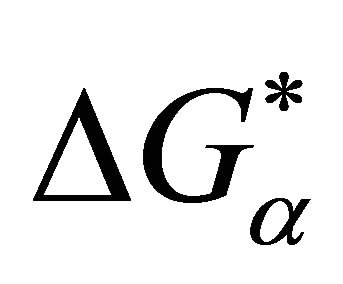 is the solvation Gibbs energy of the species
is the solvation Gibbs energy of the species ![]() and
and  is the solvent induced effect for the transition
is the solvent induced effect for the transition .
.
The relationship between the solvent-induced quantity 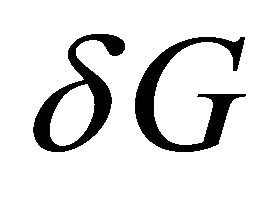 and the solvation Gibbs energies is shown in Figure 3. Note that both
and the solvation Gibbs energies is shown in Figure 3. Note that both  and
and  are determined by the solvation Gibbs energy of all the specific conformers belonging to the groups U and F. If we denote by
are determined by the solvation Gibbs energy of all the specific conformers belonging to the groups U and F. If we denote by  the Gibbs energy of solvation of a specific conformer i, then we have the relationships [20]
the Gibbs energy of solvation of a specific conformer i, then we have the relationships [20]
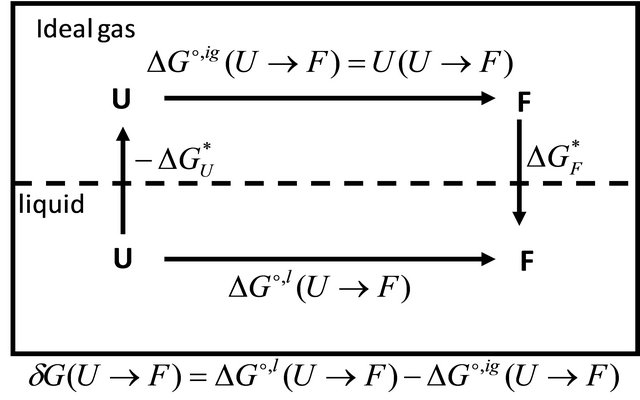
Figure 3. The relationship between the solvent induced effect , and the solvation Gibbe energies may be deduced from the cyclic process in the figure.
, and the solvation Gibbe energies may be deduced from the cyclic process in the figure.
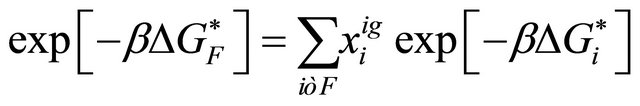 (3.2)
(3.2)
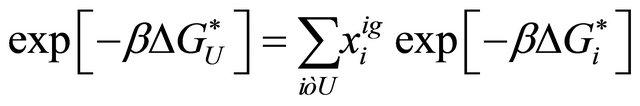 (3.3)
(3.3)
where 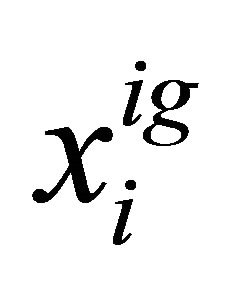 is the mole fraction of the specific conformer i in an ideal gas phase.
is the mole fraction of the specific conformer i in an ideal gas phase.
As Privalov had noted [1], according to Le Chatellier’s principle, any process which is induced by increasing temperature should proceed with heat absorption, or equivalently with an increase in enthalpy and entropy.
For the reaction (2.1) we can formulate the Le Chatellier’s principle as follows. At equilibrium we have
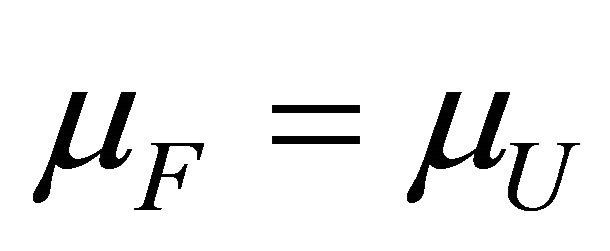 (3.4)
(3.4)
From the total derivative of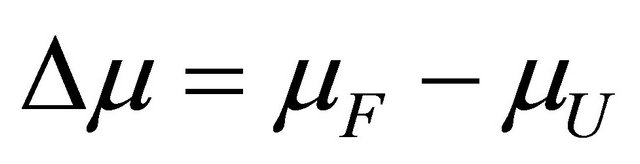 , along the equilibrium line, i.e. maintaining the condition 3.4, we have
, along the equilibrium line, i.e. maintaining the condition 3.4, we have
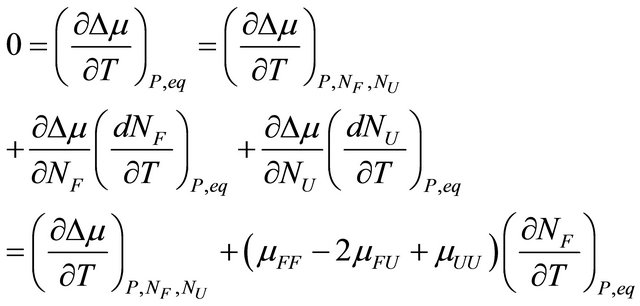 (3.5)
(3.5)
where 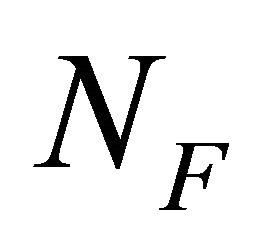 and
and 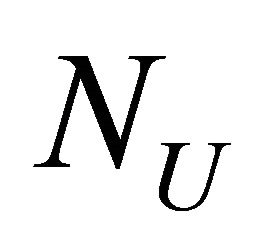 are the number of moles of F and U at equilibrium, and
are the number of moles of F and U at equilibrium, and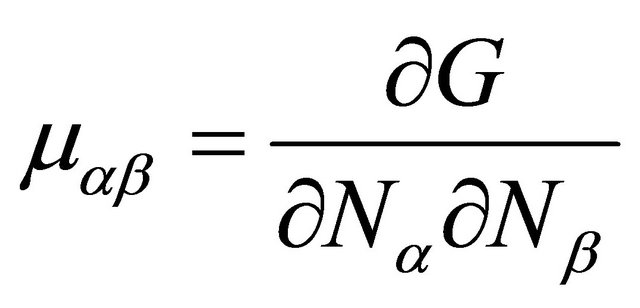 . From (3.5) we get
. From (3.5) we get
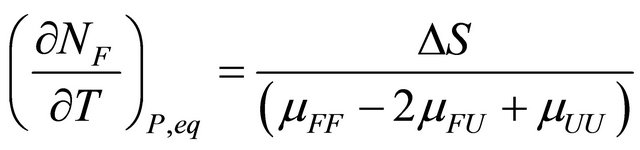 (3.6)
(3.6)
or equivalently, since 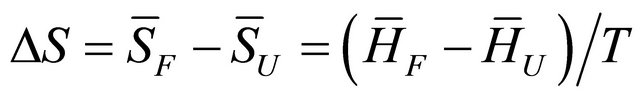 at equilibrium we have
at equilibrium we have
 (3.7)
(3.7)
The quantity 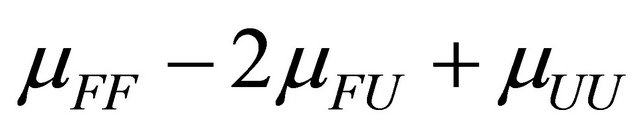 must be positive at equilibrium [20-22].
must be positive at equilibrium [20-22].
At the temperature of heat denaturation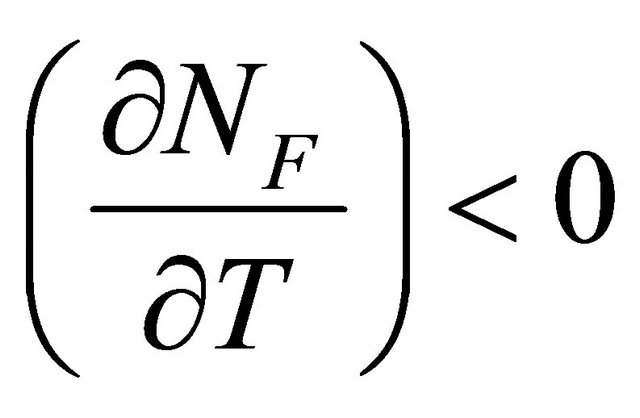 and
and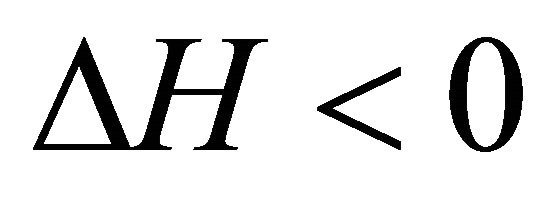 ,
,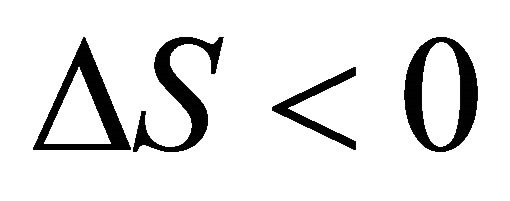 . On the other hand at the temperature of Cold denaturation
. On the other hand at the temperature of Cold denaturation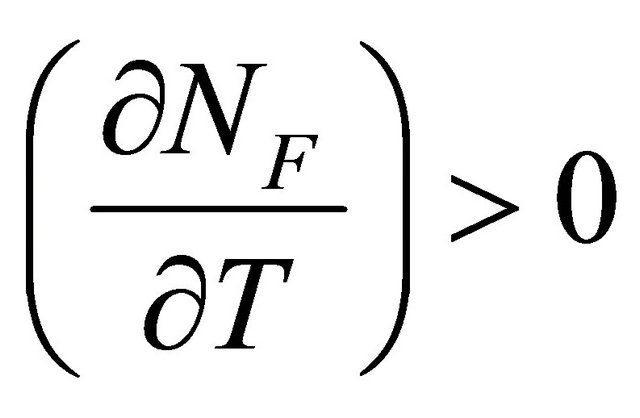 , and and
, and and
 ,
,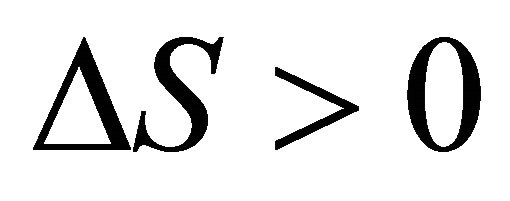 . As Privalov had noted it is relatively easy to understand the heat denaturation. The more intriguing question is to understand why
. As Privalov had noted it is relatively easy to understand the heat denaturation. The more intriguing question is to understand why  (as well as
(as well as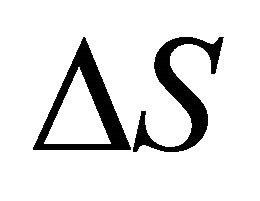 ) change signs at lower temperatures.
) change signs at lower temperatures.
The question that has concerned many biochemists was to identify the part of the solvent induced effect that is sufficiently large and negative, such that it can turn the standard Gibbs energy of the transition  from large positive to large negative.
from large positive to large negative.
The answer to this question cannot be given without a detailed examination of all the contributions to the solvent induced effect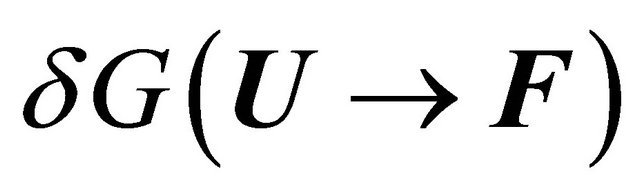 . For a long time most people assumed, based on Kauzmann’s model for the HfO effect, Figure 4, that
. For a long time most people assumed, based on Kauzmann’s model for the HfO effect, Figure 4, that 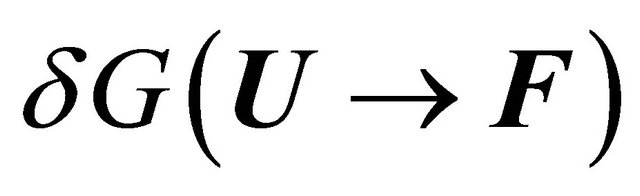 is mainly determined by the desolvation of the HfO groups, which are known to occupy the interior of the protein. Kauzmann’s ideas were ad-hoc solutions to a difficult problem. It was a brilliant idea that captured the imagination of all those who were interested in protein folding. It should be said however, that at the time when Kauzmann suggested his ideas about the HfO effect, it was also believed that intramolecular hydrogen bonding could not contribute significantly to the stability of the protein [15,21,22]. Furthermore, no other HfI effects were known at that time. Hence, the dominance of the HfO effect in protein folding was universally accepted.
is mainly determined by the desolvation of the HfO groups, which are known to occupy the interior of the protein. Kauzmann’s ideas were ad-hoc solutions to a difficult problem. It was a brilliant idea that captured the imagination of all those who were interested in protein folding. It should be said however, that at the time when Kauzmann suggested his ideas about the HfO effect, it was also believed that intramolecular hydrogen bonding could not contribute significantly to the stability of the protein [15,21,22]. Furthermore, no other HfI effects were known at that time. Hence, the dominance of the HfO effect in protein folding was universally accepted.
However, a detailed study of all the ingredients that contribute to 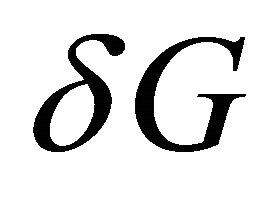 reveals that the answer to the ques-
reveals that the answer to the ques-
 (a) (b)
(a) (b)
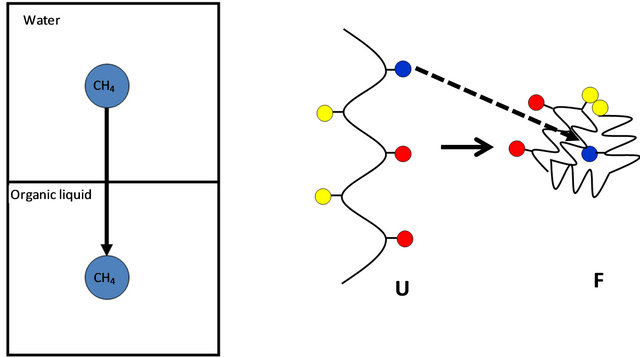
Figure 4. Kauzmann’s model for the HfO effect. The Gibbs energy of transferring a non-polar molecule, say methane from water to an organic liquid (a) is assumed to be similar in magnitude to the Gibbs energy change of a transferring a non-polar group from water into the interior of the protein (b).
tion is far from trivial. First, it was found that Kauzmann’s model, i.e. the Gibbs energy of transferring of a HfO solute from water to an organic liquid does not feature in . The Gibbs energy of transferring a HfO group attached to the protein from being exposed to water in the U conformer into the interior of the protein was found to be one or even two orders of magnitudes smaller than the estimated values of the Gibbs energy changes based on Kauzmann’s model [15].
. The Gibbs energy of transferring a HfO group attached to the protein from being exposed to water in the U conformer into the interior of the protein was found to be one or even two orders of magnitudes smaller than the estimated values of the Gibbs energy changes based on Kauzmann’s model [15].
On the other hand, a host of solvent induced effects due to HfI groups were found to be much larger than the corresponding HfO effects [22]. Therefore, it was concluded that the HfI effects are more likely to be the dominant contributor to the stability of the F conformer than any of the HfO effects.
Thus, when comparing a specific HfO effect with a specific HfI effect, one finds that the magnitude of the latter is much larger than the former. Moreover, in real proteins what determines the standard Gibbs energy of the reaction is the combined effects of all the HfO groups and all the HfI groups. If there are roughly 30% of HfO side chains and 50% HfI side chains (the other 20% are “neutral”), then a protein of M amino acids have about M/3 HfO groups, and about (M+M/3) HfI groups, the additional 2 M of HfI groups are the C=O and NH groups contributed by the backbone of the protein.
Therefore, even if each of the HfO effect had the same magnitude as the corresponding HfI effect, then we should expect that the combined effects of all the HfI groups will be larger than the combined effects of all the HfO groups. This conclusion is a fortiori true when each of the HfI effect is an order magnitude larger than the corresponding HfO effect. For more details see references [15,19]. We shall demonstrate this effect in a simple model in Section 5.
4. THE SECOND MYSTERY: WHY PROTEINS UNFOLD AS WE FURTHER LOWER THE TEMPERATURE
Having given a plausible argument, based on HfI effects, for the folding of a protein in spite of the multitude of conformations belonging to the unfolded form, answers one of the most challenging problems of protein folding [19]. Yet, an even more challenging problem is lurking when we face the phenomenon of cold denaturation.
If HfI interactions are the dominant factors that stabilize the 3D structure of the folded form, how can we explain the denaturation of the protein at lower temperatures.
Superficially, one would be tempted to embrace the HfO effect to explain the cold denaturation. It is known that the strength of the HfO effects, both solvation and pair wise interactions increase with temperature. Therefore, accepting the HfO effect as the dominant one in the folding of protein offers a plausible explanation of the cold denaturation. Namely, as we decrease the temperature, the HfO becomes weaker, hence the folded form becomes destabilized. This is the main argument given in all the theoretical approaches to the problem of CD.
Unfortunately, all the HfO effects are too weak to explain folding in the first place. Therefore, one cannot rely on the temperature dependence of the HfO to explain the unfolding of a protein at low temperatures.
A superficial argument based on HfI effect seems to lead to the conclusion that as we lower the temperature, the HfI effect will become stronger, and therefore causing further stability to the folded form. Indeed, this conclusion is true, had we only one type of HfI effect. In reality, there is a host of HfI effects, having different temperature dependence. Therefore, the answer to the question of why proteins unfold at a lower temperature is to be found in the difference in the rate of change of the various HfI effect with increasing the temperature. In the next section, we shall demonstrate this effect in a simple model. Here, we present the general argument.
First, note that one type of HfI effect operates mainly to stabilize the folded form. This is the direct intramolecular HBs between HfI groups. Others are pair wise, triple-wise, etc. HfI effects operate both on the folded and on the unfolded form. For simplicity let us assume that only one intramolecular HB is formed between two “arms” of two HfI groups (say between NH and C=O). The formation of such a HB contributes to 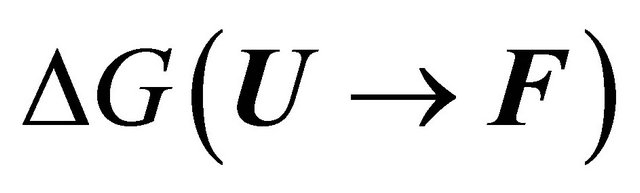 about [15]
about [15]
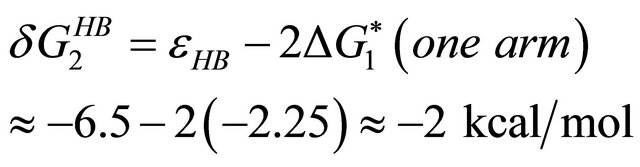 (4.1)
(4.1)
i.e. we form one HB involving energy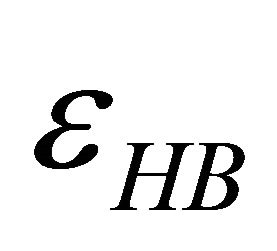 , and we lose the solvation Gibbs energy of two arms
, and we lose the solvation Gibbs energy of two arms  , which were solvated in the U form Figure 5.
, which were solvated in the U form Figure 5.
The second HfI effect is between two HfI groups at a distance of about 4.5 Å, and at the correct orientation so that they can be bridged by a water molecule, Figure 6. In this case, the contribution to the solvent-induced
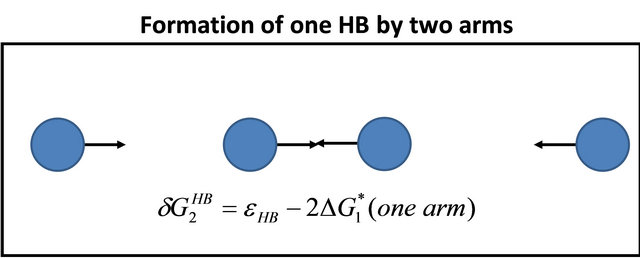
Figure 5. Formation of one intramolecular HB by two “arms” of HfI groups involve the hydrogen bond energy εHB and the loss of solvation Gibbs-energies of the two arms.
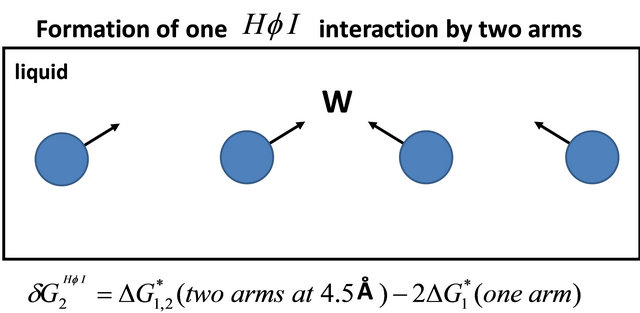
Figure 6. Formation of one HfI interaction by two “arms” of HfI groups at a distance of 4.5 Å and in the right orientation to be bridged by a water molecule.
part of the Gibbs energy is about [15]
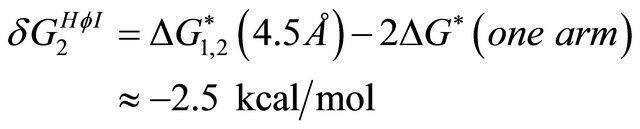 (4.2)
(4.2)
Thus, if both  and
and 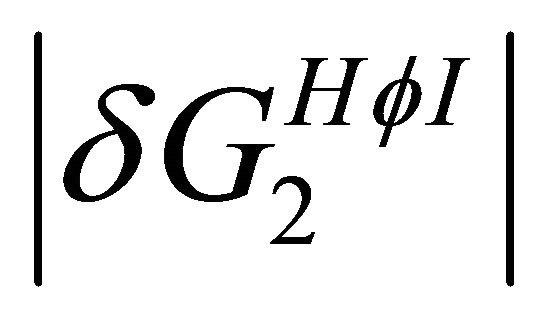 decrease upon increasing the temperature we could not expect that these two effects will cause both a stabilization and a destabilization of the 3D structure. However, from a simple model discussed in the next section, we find that these two effects have different temperature dependence, Figure 7. In this particular case
decrease upon increasing the temperature we could not expect that these two effects will cause both a stabilization and a destabilization of the 3D structure. However, from a simple model discussed in the next section, we find that these two effects have different temperature dependence, Figure 7. In this particular case  is larger than
is larger than 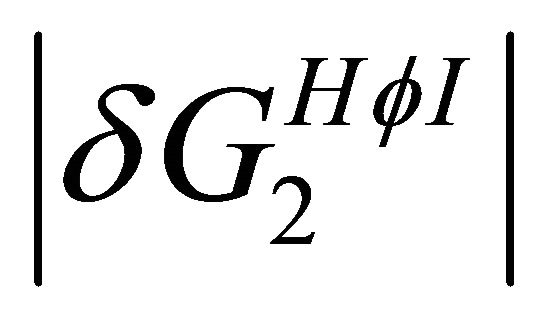 at higher temperatures. Therefore, at these temperatures
at higher temperatures. Therefore, at these temperatures 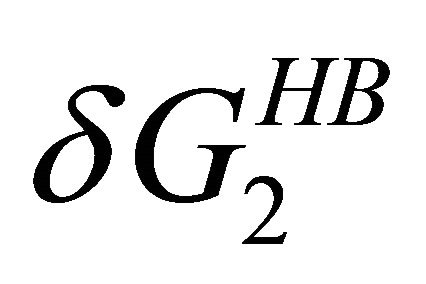 stabilizes preferentially the folded form. On the other hand, at lower temperatures the
stabilizes preferentially the folded form. On the other hand, at lower temperatures the  become the stronger effect. This HfI effect can act on patterns on HfI groups in the U form, while the
become the stronger effect. This HfI effect can act on patterns on HfI groups in the U form, while the 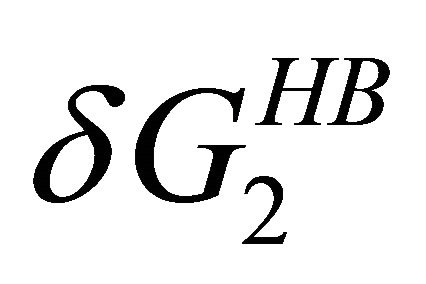 has the relatively smaller effect.
has the relatively smaller effect.
Thus, the fact that different HfI effect operates on different patterns of HfI groups, and these have different temperature dependence can explain both the heat and the cold denaturation. This is demonstrated in the next section.
5. A SIMPLE MODEL SHOWING BOTH HEAT AND COLD DENATURATION
We construct a “minimal” model for demonstrating both phenomena of heat and cold denaturation. This is a highly simplified model but it has enough real features, so as to show both transitions from U to F, then from F to U upon cooling the system.
In Figure 8 we focus on a small segment of the protein. We show here some representatives of solvent induced effects:
1) Desolvation of a HfO group in the U state.
2) Van der Waals interaction between the HfO groups and its surrounding in the F state (dashed lines in Figure 8).
3) Desolvation of a HfI group in the U state.
4) An intramolecular HBing of two arms or two HfI groups.
5) Pairwise HfO interaction (double dashed lines).
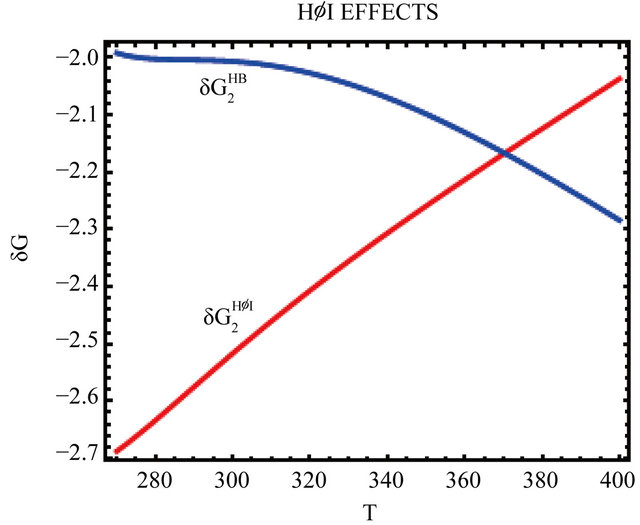
Figure 7. The temperature dependence of the two HfI effects; the formation of intramolecular HB, 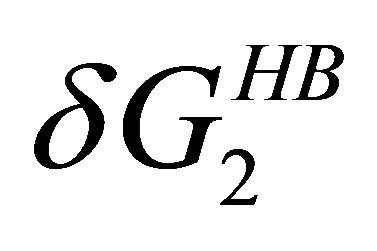 and pairwise HfI interaction,
and pairwise HfI interaction,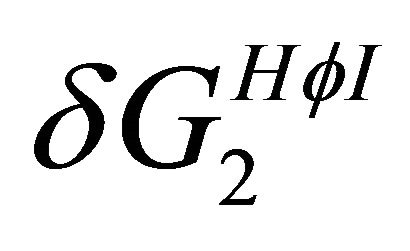 . See Section 4 for details.
. See Section 4 for details.
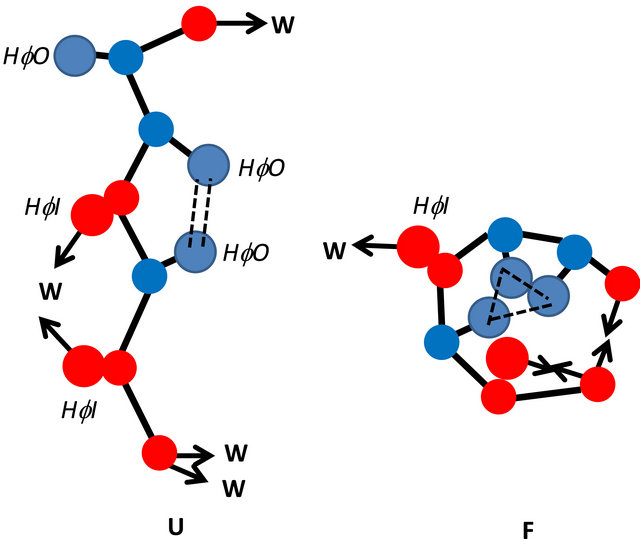
Figure 8. Illustration of a segment of a protein with three HfO side chains (blue), and five HfI arms; two belonging to side chains, and three belonging to the backbone (red). The configuration on the rhs represents the folded form F and on the lhs represent the unfolded form U. The intramolecular HBs are represented by two arrows pointing towards each other. Van der Waals interactions are represented by dashed lines and hydrophobic interaction by double dashed doube lines. A non-bonded arrow represents a solvated arm of a HfI group. Two arms pointing towards a water molecule (W) represents a pair-wise HfI interaction. This drawing does not represent a model for protein. It only serves to show the types of interactions which are taken into account in the calculations discussed in Section 5.
6) Pairwise HfI interaction (arrows pointing towards W).
A more complete inventory of all solvent-induced effect is discussed in reference 15.
The parameters we used for the following calculations are as follows:
We take the HB energy as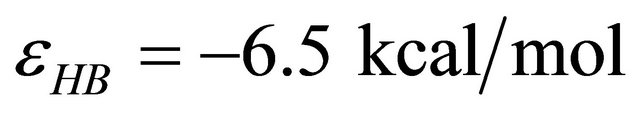 . Each van der Waals interaction contributes about −0.5 kcal∙mol. These two energies are presumed temperature independent. These are the only energies that contribute to the internal partition function of F.
. Each van der Waals interaction contributes about −0.5 kcal∙mol. These two energies are presumed temperature independent. These are the only energies that contribute to the internal partition function of F.
For the solvation Gibbs energy of a HfO group we take the value of the conditional solvation Gibbs energy of methane next to a hydrocarbon [15,22] which is about 0.35 kcal/mol at room temperature.
From the experimental date available, we take the temperature dependence of the HfO solvation to be
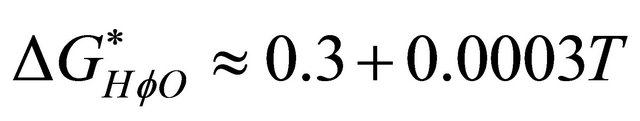 (5.1)
(5.1)
Later we shall vary the values of these solvation Gibbs energies.
For the pairwise HfO interaction and its temperature dependence we take the values [14]
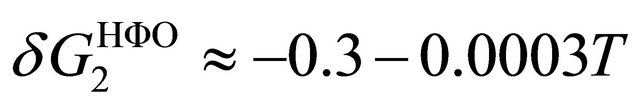 (5.2)
(5.2)
For the solvation Gibbs energy of one arm of a HfI group at room temperature we take the value of about −2.25 kcal/mol [15]. Its temperature dependence is calculated by estimating the probability of finding a water molecule in the right location and configuration to form a HB with one arm, from the equation [15,22]
 (5.3)
(5.3)
In (5.3)  is the probability that a water molecule will be found in the right position and orientation to form a HB with the arm. From the experimental values of
is the probability that a water molecule will be found in the right position and orientation to form a HB with the arm. From the experimental values of  and the choice of
and the choice of 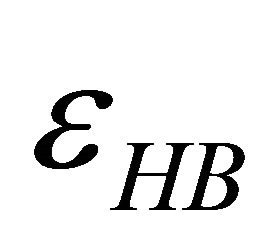 we can get the temperature dependence of the probability
we can get the temperature dependence of the probability .
.
These values are also used for the calculations of the pairwise HfI interactions between two arms [15]. Figure 7 shows the temperature dependence of the two quantities  and
and 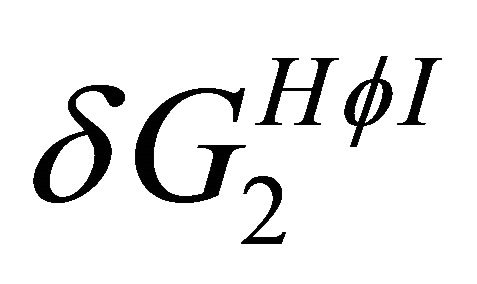 as defined in Section 4. Note the crossing of these two curves at about 370 K.
as defined in Section 4. Note the crossing of these two curves at about 370 K.
For the following calculations we assume that the segment of the protein has three HfO groups and 12 HfI groups. In real proteins the relative numbers of HfI/HfO groups is even larger than 4:1. We also assume that in the F form there are two intramolecular HBs, and three van der Waals interactions. We shall later change the values of the various interactions in order to examine the influence of each of these on the heat and cold denaturation.
The internal partition function for this system in an ideal gas phase is
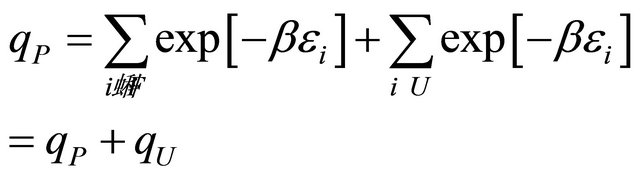 (5.4)
(5.4)
where
 (5.5)
(5.5)
In the ideal phase we assume that the lower energy level is non-degenerated, and Nc is the degeneracy of the U form. Here, we choose Nc = 1012.
The equilibrium constant in the ideal gas phase is
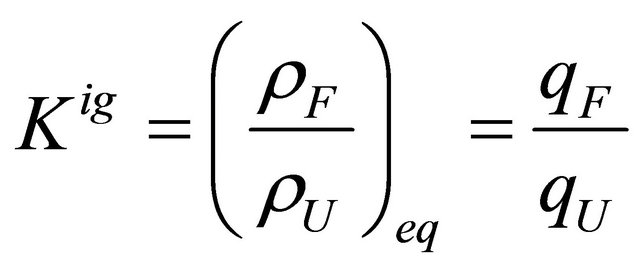 (5.6)
(5.6)
and the mole fraction of the folded form is
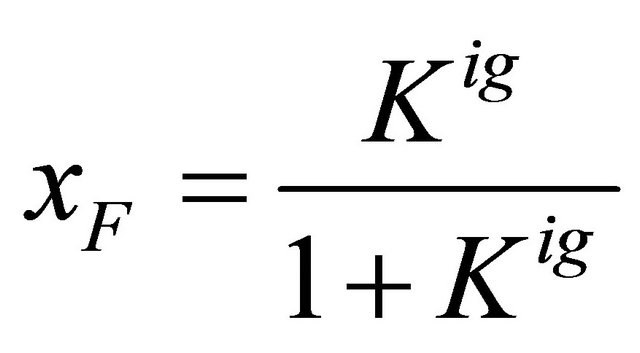 (5.7)
(5.7)
Figure 9 shows the standard Gibbs energy and the mole fraction xF as a function of T, for an ideal gas phase. As expected we see that the standard Gibbs energy in monotonically increasing function of T. We also see “folding” at temperatures of about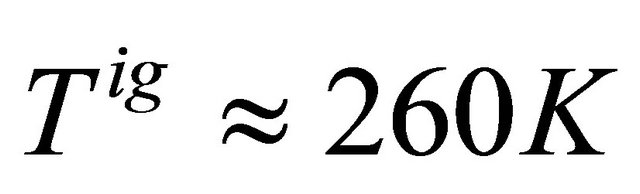 .
.
We next introduced the solvent. The equilibrium constant is changed according to Equation (3.1). In this particular calculation we have
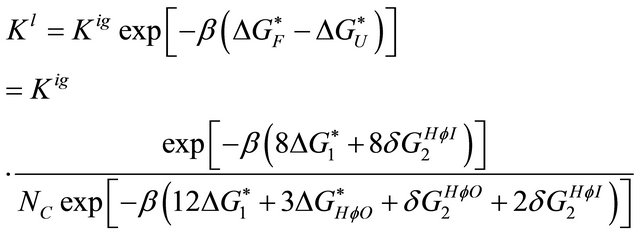
(5.8)
In the F form we have eight solvation Gibbs energies of the HfI arms and eight pairwise HfI interactions. In the F form we have 12 solvation Gibbs energies of the HfI arms, 3 solvation Gibbs energies of the HfO groups, one pairwise HfO interaction and two pairwise HfI interactions.
This particular choice was chosen for illustration of both the folding and the cold denaturation. In reality, different proteins will have different numbers of HfO and HfI groups, as well as different numbers of interactions. The following calculation is for a “typical” protein. Of course, one can multiply all these numbers by M for the whole protein and increase the degeneracy of the U form accordingly.
Figure 9 shows the results for the mole fraction of the F form
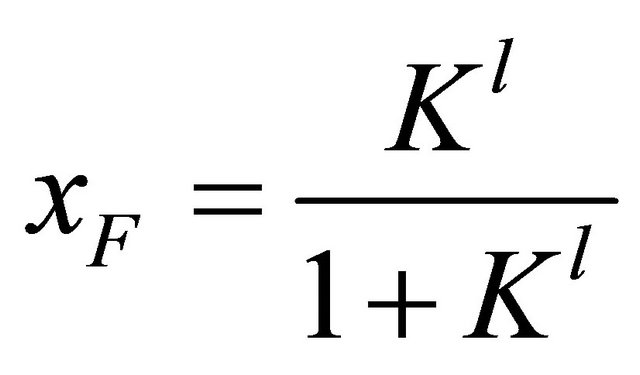 (5.9)
(5.9)
and the Gibbs energy change
 (5.10)
(5.10)
where R is the gas constant.
 (a)
(a)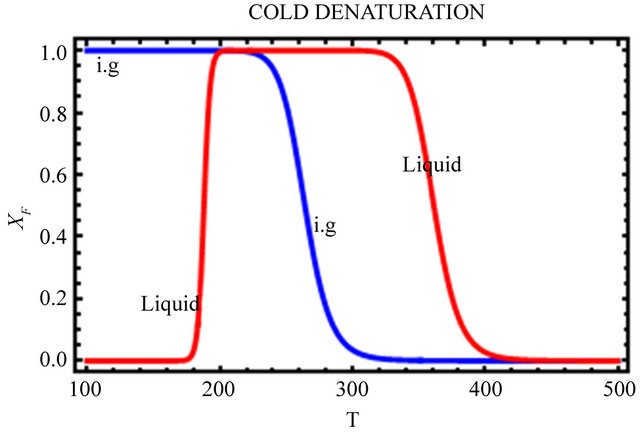 (b)
(b)
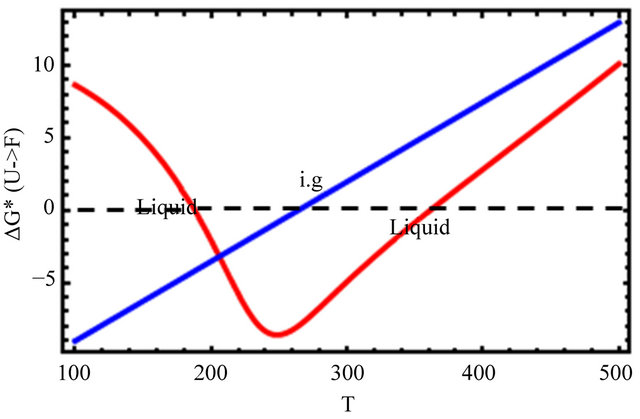
Figure 9. The Gibbs energy of folding (a), and the mole fraction of the F form (b) for the ideal gas (blue) and the liquid phase (red). Based on Eqs.5.8 and 5.10.
In Figure 9(a), we see that the standard Gibbs energy for the conversion  goes through a minimum at about 250 K, but its values are negative in a large temperature range from about 180 K to 360 K. Figure 9(b) shows the “denaturation” curve in an ideal gas phase and in the liquid phase. In the liquid phase the folding of the same protein occurs at a considerable higher temperature compared with the transition in an ideal gas phase. At about 180 K we find a steep cold denaturation which, as expected does not occur in the ideal gas phase. Note in particular the large temperature range at which the mole fraction of the F form is nearly one.
goes through a minimum at about 250 K, but its values are negative in a large temperature range from about 180 K to 360 K. Figure 9(b) shows the “denaturation” curve in an ideal gas phase and in the liquid phase. In the liquid phase the folding of the same protein occurs at a considerable higher temperature compared with the transition in an ideal gas phase. At about 180 K we find a steep cold denaturation which, as expected does not occur in the ideal gas phase. Note in particular the large temperature range at which the mole fraction of the F form is nearly one.
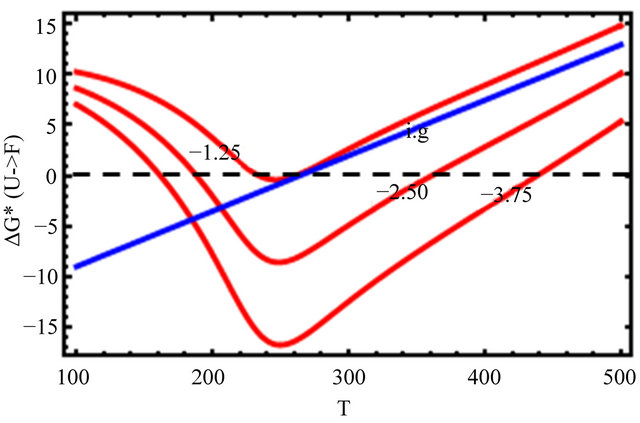
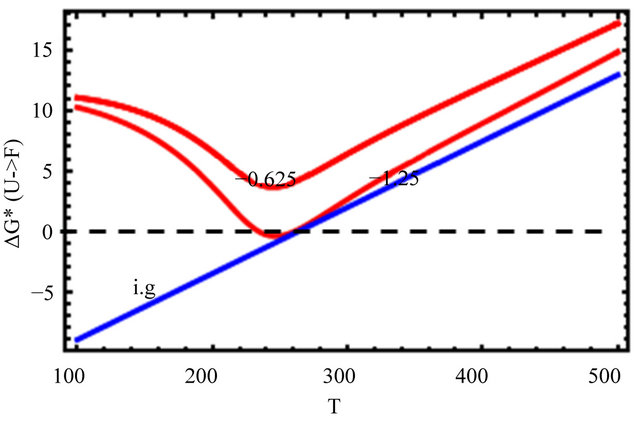
In Figure 10, we change only the HfI interactions by a factor of 0.5 and 1.5 leaving all the HfO effects unchanged. We see that as we increase the HfI interactions we get a folding at higher temperatures, and the range of temperatures at which the F form is stable increases. On the other hand, the temperature at which cold denaturation occurs is less sensitive to the HfI interactions. It occurs at slightly lower temperatures as we increase the HfI interactions. The most important finding is that when the HfI interaction is about half of
 (a)
(a)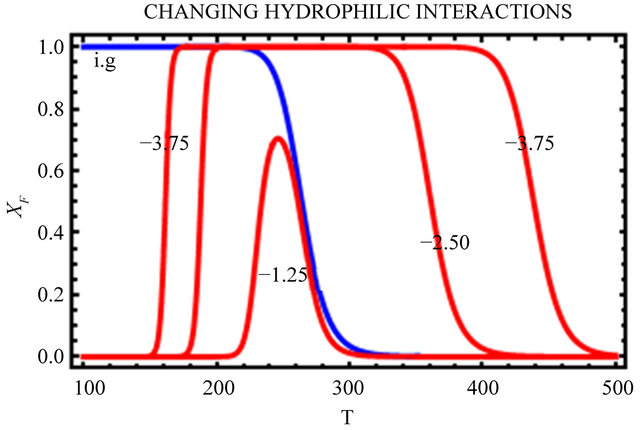 (b)
(b)
Figure 10. Same as Figure 9 but with changing HfI interaction (as indicated in the figure) above and below the values chosen in Figure 9.
its estimated value, we get folding at almost the same temperature as in the ideal gas phase, but there is no range of temperatures at which the F form is stable (i.e.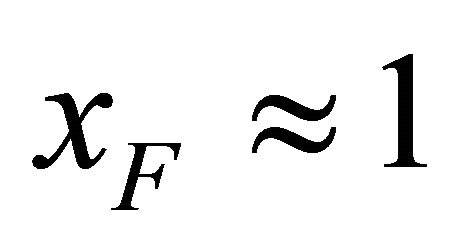 ).
).
In Figure 11, we further decrease the HfI interaction, we see that the standard Gibbs energy is everywhere positive. We do not observe folding, and there exists no range of temperatures at which the  form is stable.
form is stable.
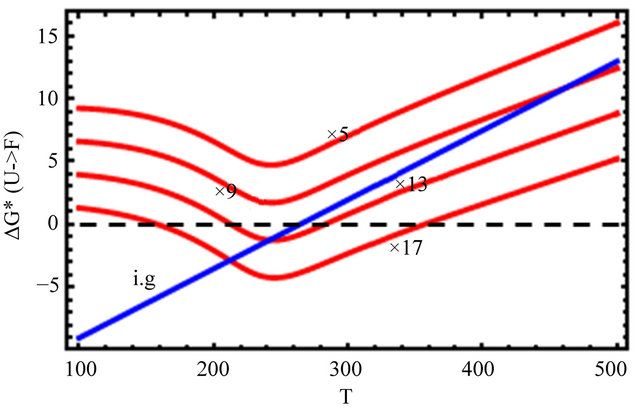
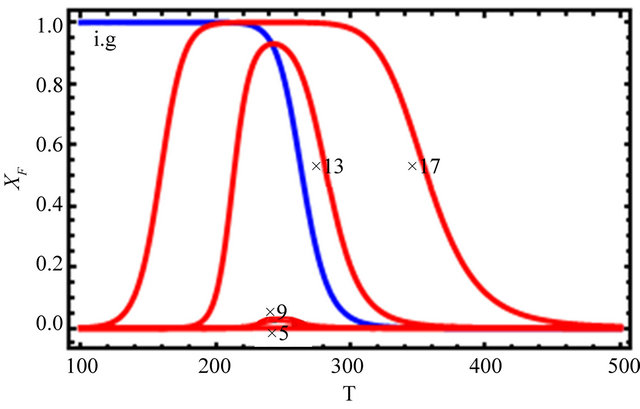
Figure 12 shows the effect of changing the HfO solvation and the HfO interactions by a factor of 5, 9, 13 and 17 (see Eqs.4.3 and 4.4). We see that one has to increase the two HfO effects by an order of magnitude or more to get folding and cold denaturation.
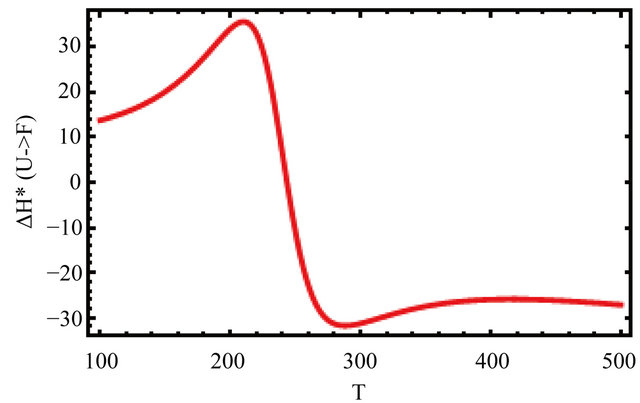
Figure 13 shows the values of the standard enthalpy of the folding ( ), and the corresponding change in the heat capacity. It is clearly seen that the standard enthalpy changes from large positive to large negative values as we increase the temperature. This is consistent with the expected values of
), and the corresponding change in the heat capacity. It is clearly seen that the standard enthalpy changes from large positive to large negative values as we increase the temperature. This is consistent with the expected values of 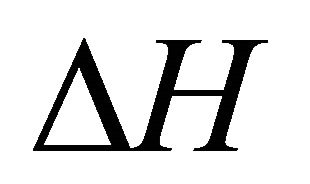 according to Equation (3.7). A detailed examination of the various contributions to the enthalpy change shows that the main contribution is the HfI effect. Figure 13(b) shows a sharp increase of
according to Equation (3.7). A detailed examination of the various contributions to the enthalpy change shows that the main contribution is the HfI effect. Figure 13(b) shows a sharp increase of
 (a)
(a)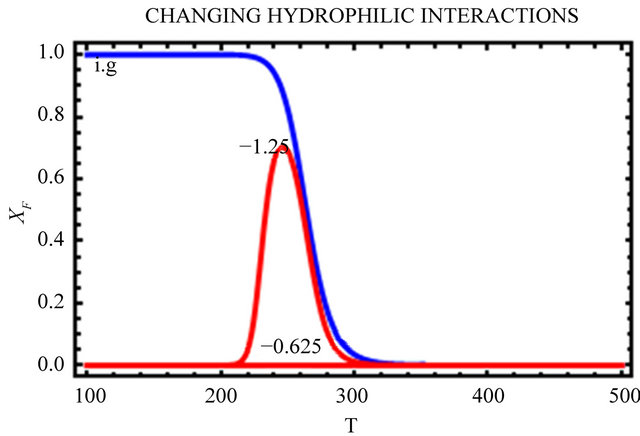 (b)
(b)
Figure 11. Further decreasing the HfI interactions by factors of 0.5 and 0.25 relative to the values in Figure 9, (as indicated in the figure).
the heat capacity change 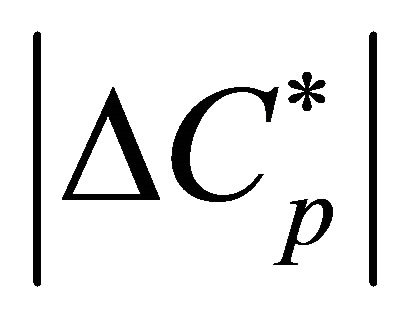 in agreement with the experimental findings [1].
in agreement with the experimental findings [1].
6. DISCUSSION AND CONCLUSION
The problem of cold denaturation (CD) is not a lesser mystery than the heat denaturation. As in the case of the protein folding problem, the search for a solution to the problem of CD has been derailed mainly because of the adherence to the myth that the HfO effects are the most important effect in protein folding [19,22].
In the highly simplified model described in section 4 we have included both HfO and HfI effects. We have the desolvation of HfO groups upon being transferred into the interior of the protein. We have pairwise HfO interaction arising from the correlation between the (conditional) solvation of the two HfO groups. We also have pairwise HfI interaction, and an intramolecular HB.
An analysis of the contribution of the various effects clearly shows that the HfI effects are the more important ones in the process of CD. One must realize that different HfI effect operates on different patterns of HfI groups. Therefore, the magnitude of the contribution of each type
(a)
CHANGING HYDROPHOBIC EFFECTS
 (b)
(b)
Figure 12. Changing the values of the HfO solvation, and pairwise HfI interaction, and no HfI interactions, (as indicated in the figure).
of HfI effect would depend not only on the particular sequence of amino acids, but also on the particular conformation of the protein.
In real proteins there are many more factors that contribute to the Gibbs energy of the process of folding. There are pair-wise, triple-wise, etc. of the HfO effects between different HfO groups, and there are many HfI effects between different HfI groups. Thus, for a protein of M amino acids we might need to consider 20 different kinds of solvations, about 202 kinds of different pairwise correlations, and more triplets and quadruplets correlations. Clearly, it is not simple to make any general statement about the main factors that determines either the folding or the unfolding of any specific protein. All we can say at the moment is that each type of HfI effect is larger than the corresponding HfO effect. Considering that a protein of M amino acids might have about M/3HfO groups, and more than 2M + M/3HfI groups, we should conclude that the combined HfI effects must be more important than the combined effects of all the HfO groups.
For the particular cases computed in Section 5 we can conclude that the explanation of both heat and cold de-
 (a)
(a)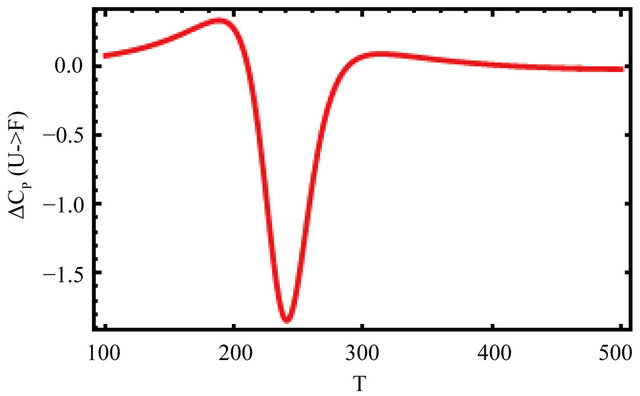 (b)
(b)
Figure 13. (a) The standard enthalpy change for the reaction  as a function of the temperature; (b) The heat capacity change for the reaction
as a function of the temperature; (b) The heat capacity change for the reaction  as a function of the temperature. Calculated for the same parameters as in Figure 9.
as a function of the temperature. Calculated for the same parameters as in Figure 9.
naturation is as follows: At high temperatures the dominating interaction is 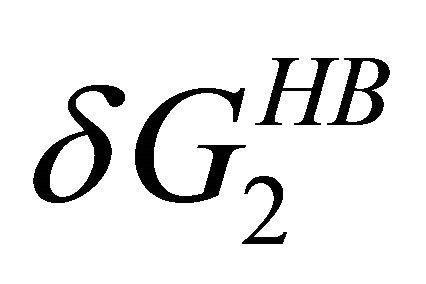 (Figure 7). This effect works to stabilize the F form. On the other hand, at lower temperatures the solvation Gibbs energy of the hydrophilic groups is larger, hence the tendency to form intramolecular HBs become weaker. This effect works to destabilize the F form. In addition,
(Figure 7). This effect works to stabilize the F form. On the other hand, at lower temperatures the solvation Gibbs energy of the hydrophilic groups is larger, hence the tendency to form intramolecular HBs become weaker. This effect works to destabilize the F form. In addition,  becomes the larger effect at low temperatures (Figure 7). This effect operated mainly on the U form, simply because in this form there are more HfI groups exposed to the solvent. Therefore, we can conclude that the variation of both
becomes the larger effect at low temperatures (Figure 7). This effect operated mainly on the U form, simply because in this form there are more HfI groups exposed to the solvent. Therefore, we can conclude that the variation of both 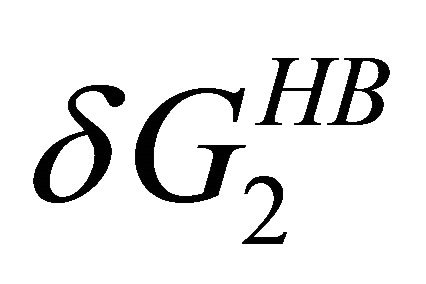 and
and 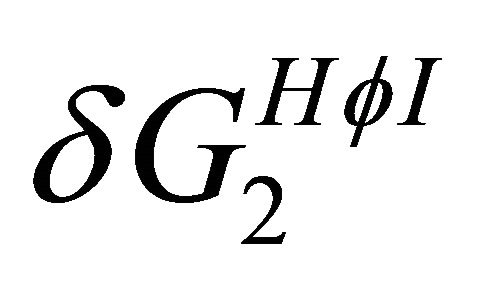 with temperature can explain both heat and cold denaturation.
with temperature can explain both heat and cold denaturation.
Having said this we might speculate on which of the HfI effects might be more important or most important in a real protein. The answer to this question is, of course sequence dependent. There are sequences for which intramoleular HB are the more important, yet there might be other sequences for which the pairwise or triplewise correlations might be more important.
Therefore, any general statement on which kind of HfI effects are the dominant ones for all proteins is at present unwarranted and perhaps an even irresponsible statement. This is a fortiori true of statements claiming that the HfO effects are the dominant ones in either protein folding or unfolding.
REFERENCES
- Privalov, P.L. (1990) Cold denaturation of proteins. Critical Reviews Biochemistry and Molecular Biology, 25, 281-305. doi:10.3109/10409239009090612
- Pace, N.C. and Tanford, C. (1968) Thermodynamics of the unfolding of beta-lactoglobulin A in aqueous urea solutions between 5 and 55 degrees. Biochemistry, 7, 198- 208. doi:10.1021/bi00841a025
- Schiraldi, A. and Pezzati, E. (1992) Thermodynamic approach to cold denaturation of proteins. Thermochimica Acta, 199, 105-114. doi:10.1016/0040-6031(92)80254-T
- Davidovic, M., Mattea, C., Qvist, J. and Halle, B. (2009) Protein cold denaturation as seen from the solvent. Journal of the American Chemical Society, 131, 1025-1036. doi:10.1021/ja8056419
- Caldarelli, G. and De los Rios, P. (2001) Cold and warm denaturation of proteins. Journal of Biological Physics, 27, 229-241. doi:10.1023/A:1013145009949
- Tsai, C.J., Maizel J.V and Nussinov, R. (2002) The hydrophobic effect: A new insight from cold denaturation and a two-state water structure. Critical Reviews in Biochemistry and Molecular Biology, 37, 55-69. doi:10.1080/10409230290771456
- Ascolese, E. and Graziano, G. (2008) On the cold denaturation of globular proteins. Chemical Physics Letters, 467, 150-154. doi:10.1016/j.cplett.2008.10.078
- Dias, C.L., Ala-Nissila, T., Kartunnen, M., Vattulainen, I. and Grant, M. (2008) Microscopic mechanism for cold denaturation. Physical Review Letters, 100, 118101- 118104. doi:10.1103/PhysRevLett.100.118101
- Adrover, E.V., Martorell, G., Pastore, A. and Temussi, P.A. (2010) Understanding cold denaturation: The case study of Yfh1. Journal of the American Chemical Society, 132, 16240-16246. doi:10.1021/ja1070174
- Graziano, G. (2010) On the molecular origin of cold denaturation of globular proteins. Physical Chemistry Chemical Physics, 12, 14245-14252. doi:10.1039/c0cp00945h
- Dias, C.L., Ala-Nissila, T., Wong-Ekkabut, J., Vattulainen, I., Grant, M. and Karttunen, M. (2010) The hydrophobic effect and its role in cold denaturation. Cryobiology, 60, 91-99. doi:10.1016/j.cryobiol.2009.07.005
- Graziano, G. (2010) Comment on “The hydrophobic effect and its role in cold denaturation”. Cryobiology, 60, 354-355. doi:10.1016/j.cryobiol.2010.03.001
- Dias, C. (2012) Unifying Microscopic mechanism for pressure and cold denaturations of proteins. Physical Review Letters, 109, 048104-048110. doi:10.1103/PhysRevLett.109.048104
- Kauzmann, W. (1959) Some factors in the interpretation of protein denaturation. Advances in Protein Chemistry, 14, 1-63. doi:10.1016/S0065-3233(08)60608-7
- Ben-Naim, A. (2011) Molecular Theory of water and aqueous solutions: Part II the role of waterin protein folding self assembly and molecular recognition. World Scientific, Singapore City.
- Ben-Naim, A.(1989) Solvent-induced interactions: Hydrophobic and hydrophilic phenomena. Journal of Chemical Physics, 90, 7412-7426. doi:10.1063/1.456221
- Ben-Naim, A. (1990) Solvent effects on protein association and protein folding. Biopolymers, 29, 567-596. doi:10.1002/bip.360290312
- Privalov, P.L. and Gill, S.J. (1989) The hydrophobic effect: A reappraisal. Pure and Applied Chemistry, 61, 1097-1104. doi:10.1351/pac198961061097
- Ben-Naim, A. (2013) The protein folding problem and its solutions. World Scientific, Singapore City.
- Ben-Naim, A. (2006) Molecular theory of solutions. Oxford University Press, Oxford.
- Prigogine, I. and Defay, R. (1965) Chemical thermodynamics. Longmans, Green and Co., London.
- Ben-Naim, A. (2009) Molecular theory of water and aqueous solutions, Part I: Understanding water. World Scientific, Singapore City.

