Received 13 October 2014; revised 11 November 2014; accepted 5 December 2014

ABSTRACT

The Schrödinger perturbation energy for an arbitrary order N of the perturbation has been presented with the aid of a circular scale of time. The method is of a recurrent character and developed for a non-degenerate quantum state. It allows one to reduce the inflation of terms necessary to calculate known from the Feynman’s diagrammatical approach to a number below that applied in the original Schrödinger perturbation theory.

Keywords:

Quantum-Mechanical Perturbation Energy, Circular Scale of Time

1. Introduction

The conceptual background of quantum mechanics seems to be inadequate when the perturbation methods are considered; see e.g. [1] . This also holds true when the problem of a time-independent perturbation applied to a non-degenerate quantum state is considered.

On one side a complicated Schrödinger formalism should be applied, [2] , yet on the other side an inflation of terms, provided by the diagrammatical method based on the Feynman classification of the perturbation process, completed with the aid of the time variable comes into play [3] [4] . Both methods can be tedious to follow especially when a large perturbation order 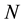is taken into account.

The aim of this paper is to address these highlighted problems by applying a circular scale of time with diagrams. Several steps in this direction have previously been achieved [5] - [7] . However, an additional simplification of the approach can be attained when partition of the order number 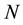into separate components is taken into account.

The present contribution combines the results obtained from both the circular scale and the partition properties of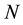. This method allows us to calculate the Schrödinger terms for energy for an arbitrary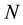. The presentation commences with an outline of a theory relating to time.

2. Subjective Character of the Notion of Time

Time scale is represented by a sequence of events (time points) with different intervals between them.

If we are travelling by train for example, we do not really need to rely on a watch to observe time lapse as it is sufficient to study the station names. By analysing the stations we are able to estimate not only the geometrical distance from the point of our departure, but get also an idea of time progression. The only knowledge we need is a sequence of stations extending along our trip. If we do not insist on the accuracy of the intervals of time, we can satisfy ourselves to know that “nearer” means an earlier station in time, whereas a “further” station means a later moment in time.

Obviously this kind of parallelism holds true irrespective of the type of track along which the train is travelling, although the tracks can vary in terms of their shape. One type, for example, is that we are systematically further from our departure point, but it could also be a different type of track―perhaps circular in nature. This would mean that after travelling through several stations the train arrives at its original departure point. Then comes an important aspect of the journey. If the track crossing the departure-end station is the only one, its effect on the train―if it preserves its motion (including the motion direction)―is to repeat its trip along the same set of stations as before.

Another scenario may occur however, if we assume that there is a possibility for the train to choose to travel upon a differing track at its original departure end point. Without going into details, a natural conclusion is that a journey along an alternative track will be different than that of a former one.

This simple example depicted above connecting time with a track can raise a question concerning our concept of time in general. From childhood we are accustomed to a notion of time which is associated with change. If daily events were to be essentially the same, we could need a watch to track each day as otherwise no distinction between them could be realised.

In practice, however, a completely different picture is inscribed in our memory―nothing, or almost nothing, repeats itself completely. This means that in all our observations we can find occurrences that do not repeat themselves. Therefore this supports a conclusion that time behaves like a train as in the first example quoted above. No station is repeated, time is progressing from a start point to an arbitrarily distant moment in the future. As it is easy to understand that our start point can be considered by other observers as a rather advanced point in time, we can easily also relate to a concept of the past. This notion―considered in an opposite direction to our everyday experience of progressing time―can classify events at an arbitrarily greater distance from us. Quantitatively, the past distance becomes similar to the notion of a distant future.

In effect, if we numerate the events, we obtain a sequence of the form

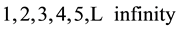(1)

for the future, and

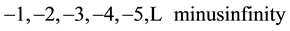(2)

for the past.

Certainly the scale of time, being a result of our observational knowledge and imagination, is not the only one which can exist. Let us consider an atom which is not influenced by any external or internal factor. For example an atom of a non-radioactive element which in its ground state can remain static for an infinitely large set of measurements undertaken by an observer. This set can be represented, for example, by a sequence of constant numbers, say

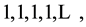(3)

since the effect of the first measurement does not vary with the next ones, on condition the measurements do not influence the atom.

A slightly more complicated illustration is that of a periodic mechanical system, for example represented by the electron moving in a hydrogen atom described by the Bohr-Sommerfeld atomic theory; see e.g. [8] . Let us assume that the electron is moving along an elliptical planar orbit. When two electron positions on the orbit, for example the nearest to the nucleus and the most distant from that object, are solely considered, we obtain a set of observations labelled by the numbers

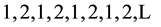(4)

The set can be made infinitely long because no change of two special electron positions in the atom mentioned above can be attained in the absence of the system perturbation. Obviously more complicated sets of repeated numbers than (4) can represent more complicated periodic systems.

A characteristic point is that not only in classical physics, but also in quantum theory, we follow the scale of time of (1) and (2) which is typical for everyday life. According to this scale the events labelled by time do not repeat themselves. Our aim is, in the first step, to point out that an application of such scale in the quantum theory is not really justified. To this purpose a time analysis of the quantum-mechanical perturbation problem within the formalism introduced by Schrödinger will be carried out.

3. Schrödinger and Feynman Approaches to the Perturbation Problem of a Quantum-Mechanical System

Schrödinger based his approach to the quantum theory of the atomic systems on the property of duality represented by the particle-like and wave-like pictures of the matter. The Hamiltonian operator on which the approach is based is in fact similar to that of a moving particle. However the operator of the particle momentum is chosen in the way that it gives an equation for a wave associated with the examined particle. A well-known fact on such an approach is that it gave very satisfactory practical results. When solved accurately, the Schrödinger wave equation could produce very accurate data on numerous observables from the atomic world. This especially concerned the electron energy of atoms.

The point raised by Schrödinger himself was that, in general, his treatment becomes a very complicated mathematical task for relatively simple systems. Such a situation exists when a rather simple atom is influenced by an external field, for example of an electric or magnetic character. To avoid the difficulty of solution of his equation also being valid in this case, Schrödinger proposed to consider the potential of an external field as a small perturbation of the potential governing the atom in the absence of any external influence. In consequence, the perturbation formalism operates with the wave functions describing the states

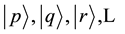(5)

and energies

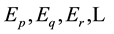(6)

of an unperturbed quantum system together with the perturbation potential

(7)

characteristic for an external physical effect.

On many occasions it can be assumed that (7) does not depend explicitly on time but is a function solely of the position vector, so it can be said that (7) represents a time-independent perturbation problem. Another assumption which facilitates the approach is that the unperturbed state is non-degenerate.

In fact, in order to solve the perturbation problem, Schrödinger developed a complicated formalism which does not apply the notion of time at all. This was possible because both the beginning state of an unperturbed system (atom) and the state obtained in effect of the perturbation, are assumed to be stationary and therefore independent of time. When limited to the calculation of the perturbation energy, 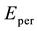, the method gradually attains the form of components of the series which is

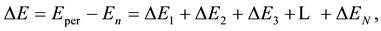(8)

on condition we assume that the series is convergent and N is large enough to give a good approximation for deltaE. In practice the complication of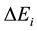, and therefore also entering (8), increases very rapidly with the increase of and N. Therefore the calculation also depends on the patience of the calculating person, or equipment, which can be an important parameter. If we focus our attention on, the number of kinds of the perturbation terms entering this energy component increases with N according to the formula [9] [10]

(9)

More than twenty years after Schrödinger’s method, Feynman classified quantum events according to their dependence on time. In effect a formalism suitable to calculate the sum in (8) has also been developed.

However this calculation did not follow, in general, the series of presented by Schrödinger. In fact the number of Feynman terms represented by diagrams necessary to calculate in (8) is

(10)

(see [4] ). This number for large heavily exceeds the number. In effect, in order to obtain an individual perturbation term entering in (8), very many Feynman terms indicated by in (10) should be combined. For example for we have

(10a)

whereas the number

(10b)

Thus (10a) and (10b) imply that on average approximately about

(11)

Feynman terms should be combined in calculating an individual Schrödinger perturbation term entering. This task can be difficult to realize even with the aid of the computer programming.

However, the scale of time applied by Feynman does not in fact difffer, from the conventional scale presented in (1) and (2): there is no limitation, or constraint, imposed on the time variable applied in that scale. Our aim is to present in Sections 4 and 5 an approach where time is classified according to a scale which is different than that characterized by (1) and (2). This is a scale represented by a topological circle, or is composed of a set of such circles. Efficacy of the scale obtained in this way in calculating the Schrödinger perturbation terms becomes evident.

4. Scale of Time Suitable for the Schrödinger Perturbation Theory

In general this kind of scale is circular in its nature, since it is based regularly on a loop of time being a topological circle. A single circle, called the main loop of time, is characteristic for any. But for the main loop scale should be supplemented by the scales having side loops. Qualitatively the side loops are similar, but not identical in their character, to the main loop.

The details of the scale depend on the order number of the perturbation. If we assume that perturbation of a system is an effect of its interaction with, can be regarded as a number of the system collisions with in course of a single cycle of collisions. The time moments of collisions are indicated on the loops by points. So, for example, the loop belonging to has 7 time points on it. For any there exists a single scale composed of only one loop of time and having no side loops. But beginning with there occurs, beyond the main loop of time, other scales which have one or more side loops attached to their main loop. Evidently the main loop on a supplementary scale is submitted to deformation because of the presence of the side loops.

An important point is that the total number of scales, or diagrams representing them, which can be constructed is equal to. Therefore for we have kinds of the perturbation terms and 132 scales (diagrams) which can be obtained: one scale is equal to a single loop, the 131 diagrams possess one or more side loops. In these 132 diagrams set, no identical diagrams can occur. This does not mean, however, that all 132 energy components entering and represented by the diagrams are different.

Examples of diagrams for are given in Figure 1.

For any the diagrams having side loops are obtained due to contractions of time points present on the original single main loop of time which has no contractions and consequently no side loops. The rule governing contractions is that the lines on diagrams obtained in effect of contractions do not cross [5] .

This is a sufficient condition to obtain all contracted diagrams for a given. One point on each main loop of time (original or deformated by the presence of the side loops), called the beginning-end point, cannot be submitted to contractions. All other time points, including those present on the side loops, can take part in contractions. Since the side loops have their own beginning-end points, the property of possible contractions of these points with other points of time located on the same loop represents the main feature distinguishing the side loops from the main loop.

Because any diagram represents one kind of the Schrödinger kinds of the perturbation terms ascribed to a given, a problem arises in presenting these kinds in a possibly compact form. Several rules elaborated before for diagrams allowed us to perform this task. However, the presentation of the diagrams and their analysis do not seem to be a convenient method in calculating the energy terms when is large. To avoid this difficulty an algebraic approach to the energy calculation is developed and presented in subsequent sections of the present paper.

5. Partition of the Number into Its Integer Components and Calculation of the Energy Terms

One kind of the energy terms, namely that corresponding to a single, called main or uncontracted, loop of time is very easy to calculate. For example for this kind of energy terms becomes

(12)

The number of P’s is equal to, and the number of V’s is equal to. Since state is perturbed, we have for V the matrix elements of the kind

(13)

whereas the P’s entering (12) are subsequently the reciprocal energy terms:

(14)

For an uncontracted diagram all powers of P are equal to 1 (see (12)), but for contracted ones at least some of the powers of P, as well as those of the terms entering (14), can be larger than 1.

Evidently the summation process over the indices and u which have to be performed in (12), or in similar terms obtained due to contractions and enclosed within the brackets, does omit the index n of the quantum state submitted to perturbation. The superscript per applied for the perturbation potential in (7) has been henceforth neglected for the sake of brevity.

One of the points of time on the loop (the beginning-end point) is free of manipulations like summation or contraction. Let us label it by 7 and attribute to state n. Consequently the points 1, 2, 3, 4, 5, and 6 on the same loop can be attributed respectively to, and u. Since point 7 represents a passive attitude in further calculations, we have in fact 6 points of time to our disposal as contraction points.

The partitions of 6 into components, beginning with the lowest terms is represented in Table 1, the number of partitions being equal to. In the 3rd column of Table 1 we give the number

The sum of 32 entering the table is.

which is a product of, where are the numbers entering a given partition and are obtained from the Formula (9) (is substituted for each number entering partition). A characteristic point is that a sum of for all partitions in Table 1 is equal to.

In order to obtain the energy terms, it can be noted that the component numbers entering partitions which are larger than 1 can be submitted to partitions they own. In fact it is of use to submit to partitions only the numbers

(15)

For example for we obtain 1 in (15), so only a single partition is present:

(16)

This result is associated with the first order perturbation term

(17)

which enters as a factor multiplying the result obtained from the main loop of time given in the form of the product of V and P enclosed within the brackets; see Tables 2-4.

On the other hand, for the partitions of the number

(18)

are

(19)

and

(20)

The energy terms multiplying the contribution coming from the bracket term given by the main loop of time are respectively:

(21)

for partition (19), and

(22)

for partition (20). Similar partitions can be done for

(23)

which come from presented in Table 1. The resulted energy terms are given in Tables 2-4.

A characteristic point is that the exponents of’s in Tables 2-4 change with partitions taken into account after the bracket terms. This is an effect of the change of the number of the terms which have to be taken into account as a result of partitions. This point is made more evident in Table 4 where the energy terms are correlated with partitions done in the case of a single number

(24)

Also the for partitions of the number 5 and their sum are given explicitly in this case.

A general rule for the exponents of and partitions is connected with the number of energy terms which are present after the bracket term. When only one energy term is present after the term, this means that only a single contraction of the time points has been done on the main loop. In effect of such contraction the exponent of―which is at place of the time point where contraction is present―changes (increases) its value by one giving

(a) The remaining four contractions are:, , and; (b) The remaining four contractions are:, , and.

(a) Other 13 contractions are:, , , , , , , , , , , ,; (b) Other 4 contractions are:, , ,; (c) Other 4 contractions are:, , ,.

(25)

in case of presence of the product of two energy terms after this exponent of increases by two:

(26)

etc. The maximum increase of the exponent is dictated by the number submitted to partition which is 5 in the examined case, so the exponent of is then

(27)

Let us note that in Table 4 we have the bracket term with only one P⁶ inside. This correlates with a single number which is taken into account in partitions of; see Table 1.

In Appendix the energy terms for and 6 are calculated in the same way as for above.

The sign of an energy term is dictated by the number of loops entering the diagram, or―which is perhaps more suitable to apply in case of the present paper―the number of factors entering the energy term:

(28)

More briefly, the term is taken with a positive sign for an odd, but enters with a negative sign for an even.

6. Summary

In the paper we presented a way of calculating the Schrödinger perturbation energy by a method which can be easily extended to large perturbation orders N. A non-degenerate quantum state and its perturbation by a time-independent potential are examined.

The method, in its original shape, has applied a circular scale of time with contractions of the time points present on the scale. By contraction of all time points on the scale (beyond the beginning-end point) in the way that no contraction lines drawn between the points can cross together, the number of kinds of the energy perturbation terms known from the Schrödinger theory, as well as simple formulae for calculating these terms, could be obtained [5] -[7] . In the present paper the same aim is accomplished in a more compact, namely algebraic way. In this case the partitions of the number

(29)

are of use. An advantage of the algebraic approach is that it can be readily extended to an arbitrary order N.

A similar time scale and algebraic method based on it have been applied before [11] in deriving the recurrence formulae for. A general view on the earlier approaches to the method is given in [12] .

References

Appendix: Terms of the Schrödinger Perturbation Energy Belonging to Orders from to

The perturbation energy of orders and can be represented by single terms which are

(A.1)

and

(A.2)

for notation see Section 1 of the main text.

The perturbation energy of order is composed of two terms corresponding to the following partitions of:

(A.3)

(A.4)

The terms are respectively

(A.5)

(A.6)

The perturbation energy of is a sum of the five terms coming from the following partitions of:

(A.7)

(A.8)

(A.9)

(A.10)

The terms are

(A.11)

(A.12)

(A.13)

(A.14)

It can be noted that partition (A.10) gives two terms entering (A.14). Henceforth the number of kinds of the perturbation terms represented by a given formula is indicated in brackets

For partitions of are of importance:

(A.15)

(A.16)

(A.17)

(A.18)

(A.19)

(A.20)

(A.21)

(A.22)

They give respectively

(A.23)

(A.24)

(A.25)

(A.26)

(A.27)

(A.28)

(A.29)

(A.30)

(A.31)

(A.32)

(A.33)

(A.34)

(A.35)

Partitions (A.19) and (A.20) give each two kinds of terms since, they are (A.27) and (A.28) for (A.19) and (A.29) and (A.30) for (A.20).

Partition (A.22) gives five kinds of terms since They are represented by (A.32) which contains two kinds of terms because has two components, and by (A.33), (A.34) and (A.35) any of which provides a single component to. This is so because. The corresponding to each kind of terms presented in (A.23)-(A.35) are given in brackets after the symbol of these terms.

A characteristic point concerning the numbers given in brackets from (A.23) to (A.35) is that their sum is equal to.

The calculation of is connected with partitions of. They are

(A.36)

(A.37)

(A.38)

(A.39)

(A.40)

(A.41)

(A.42)

(A.43)

(A.44)

(A.45)

(A.46)

(A.47)

(A.48)

(A.49)

(A.50)

(A.51)

The partitions provide us with which is a sum of the following kinds of terms:

(A.52)

(A.53)

(A.54)

(A.55)

(A.56)

(A.57)

(A.58)

(A.59)

(A.60)

(A.61)

(A.62)

(A.63)

(A.64)

(A.65)

(A.66)

(A.67)

(A.68)

(A.69)

(A.70)

(A.71)

(A.72)

(A.73)

(A.74)

(A.75)

(A.76)

(A.77)

(A.78)

(A.79)

(A.80)

(A.81)

(A.82)

(A.83)

(A.84)

(A.85)

Let us note that any partition having 3 as its component [(A.44)-(A.46) and (A.49), (A.50)] provides us with two kinds of terms, partition having 4 provides us with five kinds of terms, and partition equal to 5 gives 14 kinds of terms because. The same multiplicity concerns: the energy term having index corresponds to two kinds of perturbation terms and that having index corresponds to five kinds of perturbation terms. The sum of the given in brackets from (A.52) to (A.85) is equal to.

A characteristic point is that if some number is entering partition of, the indices of corresponding to the side loops obtained in effect of the presence of that satisfy the partitions of the number; see e.g. the set of in (A.78)-(A.85) due to the presence of partition (A.51). Evidently the largest will be that equal to; see (A.78).