Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:43825,10 pages DOI:10.4236/jqis.2014.41005
Super Quantum Discord and Inferior “Geometric Discord” Based on Weak Measurement in Noninertial Frames
Maohuai Xiang, Jiliang Jing*
Department of Physics, and Key Laboratory of Low Dimensional Quantum Structures and Quantum Control of Ministry of Education, Hunan Normal University, Changsha, China
Email: *jljing@hunnu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 January 2014; revised 16 February 2014; accepted 4 March 2014
ABSTRACT
Instead of projective measurement, we use weak measurement to define quantum and geometric discords, and compare them with the normal quantum and geometric discords based on the projective measurement in noninertial frames. We find that using weak measurement to define quantum discord we can capture more quantum correlations compared with the projective measurement, so calling it super quantum discord. However, we note that the geometric discord based on the weak measurements becomes smaller, so we name it inferior “geometric discord”. We also show that, although both the super quantum discord and the inferior “geometric discord” decrease with the increase of observer’s acceleration, the super quantum discord/inferior “geometric discord” increases/decreases as the measurements become weak. These differences reveal that the definitions of the quantum and geometric discords are not too concordant with each other.
Keywords:Weak Measurement; Super Quantum Discord; Inferior; Geometric Discord

1. Introduction
The integration of quantum information and another fundamental theory of modern physics—relativity theory creates the relativistic quantum information [1] [2] . Understanding quantum information in relativistic framework is crucial from fundamental perspective. What’s more, many experimental setups, to improve the experimental precision, require us to consider such effects coming from relativity in practice, so this field has been attracted much attentions [3] -[7] recently. Entanglement, one of the most general quantum resource for quantum information tasks, has been studied fruitfully in noninertial frame [4] -[7] . However, as we all know, the entanglement has no advantage in some quantum information tasks, since certain quantum information processing tasks can still be done without it [8] -[10] . Another quantum resource called quantum discord [11] -[13] , which represents the inaccessible information that cannot be extracted by measurements on one subsystem and is defined as the difference between the total and the classical correlation, is believed more practical and generalized than the entanglement. In this regard, Datta [14] calculated the quantum correlation between two relatively accelerated scalar modes, and showed that the quantum correlation that is measured by the quantum discord is greater and more robust than the entanglement. They claimed that the quantum discord, unlike the entanglement, still conserve a finite amount although in the limit of infinite acceleration. Wang et al. [15] studied the quantum discord and classical correlation sharing between modes of Dirac fields in the noninertial frame and discussed the relations between the quantum discord and the entanglement, and compared them with that for the Bosonic field. Besides, the geometric discord [16] [17] , which is considered to be the geometric version of the quantum discord and defined as (the square of) the Hilbert-Schmidt distance between the state in question and the nearest classical state, is also studied together with the relativistic effects [18] [19] . It should be pointed out that, although both the quantum and geometric discords can characterize the quantum correlations, some authors found that these two quantities are not too concordant with each other. M. Okrasa and Z. Walczak [20] pointed out that quantum discords do not give consistent results, namely quantum discord and the geometric discord do not necessarily imply the same ordering of two-qubit  -states, which means that
-states, which means that 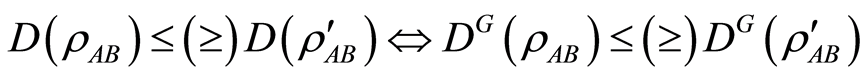 is not satisfied for arbitrary states
is not satisfied for arbitrary states 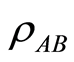 and
and . M. Piani [21] showed that the geometric discord has a problem that it can increase even under trivial local reversible operations of the party whose classicality or nonclassicality is not tested, while the quantum discord does not. Besides, E. G. Brown [18] even found that the geometric discord vanishes for Bosonic field in the infinite acceleration limit, but the quantum discord still exists, which shows the distinct different results between the quantum discord and the geometric discord.
. M. Piani [21] showed that the geometric discord has a problem that it can increase even under trivial local reversible operations of the party whose classicality or nonclassicality is not tested, while the quantum discord does not. Besides, E. G. Brown [18] even found that the geometric discord vanishes for Bosonic field in the infinite acceleration limit, but the quantum discord still exists, which shows the distinct different results between the quantum discord and the geometric discord.
It is well known that the quantum discord is measurement dependent, and an optimal measurement process should be considered during its calculations. Generally speaking, authors ordinarily use the projective measurement to define the quantum discord and the geometric discord. It is worthy to note that quantum states are fragile to quantum measurements, and they will lose all the coherence after the projective measurement. However, unlike the projective measurement, weak measurement, which was firstly proposed by Aharonov, Albert, and Vaidman (AAV) [22] in 1988, can induce only partial coherence of quantum states to be lost because it couples the system and the measuring device weakly, and then causes small change to quantum states. Let’s note that the weak measurement has been discussed universally in different fields [23] -[25] , such as geometric phase [26] . Especially, Uttam Singh and Arun Kumar Pati recently used the weak measurement to define quantum discord [27] instead of the projective measurement, and they surprisedly found that weak measurement can capture more quantum correlation, and the super quantum discord can be potentially a useful resource for quantum computation, quantum communication and general quantum information processing tasks. They also have proved that the super quantum discord in the post measured state is equal to the difference between the super quantum discord and the normal quantum discord in the original state, and therefore the weak measurement has the ability to resurrect the lost quantumness of any composite quantum state [28] . After their works, Y. Wang et al. [29] considered super quantum correlation and geometry for Bell-diagonal states with weak measurements. Besides, B. Li et al. [30] gave the necessary and sufficient condition for vanishing super discord. They also discussed the advantage of the weak measurement [31] and analysed the property of the weak measurement in quantum discord [32] .
The previous studies on quantum correlation are almost based on the projective measurements and confined in inertial frames. To find out how the measurements affect the quantum correlation and give a more complete frame to theoretically study it, in this paper we will define the quantum discord and its geometric version by using the weak measurement, and extend them to the noninertial frame. We will also discuss their reactions to the strength of measurements and the acceleration of observer and then compare them with the quantum correlation based on the projective measurement. Fortunately, we find some inconsistent results of the quantum and geometric discords from the perspective of the weak measurement.
The outline of the paper is as follows. In Section 2, we introduce the definitions for the quantum discord and geometric discord based on both projective and weak measurements. In Section 3, we analyse the entangled state of Dirac fields when the two observers relatively accelerates, and consider the quantum and geometric discords based on the weak measurement in noninertial frame and compare them with the normal versions. We summarize and discuss conclusions in the last section.
2. Definitions for Quantum Discords
To study the quantum and geometric discords based on the weak measurement and compare them with that based on the projective measurement, in this section, we introduce the definitions for the quantum discord and geometric discord based on these two different measurements.
2.1. Normal Quantum and Geometric Discords
For a bipartite quantum state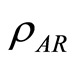 , the total correlation is defined by
, the total correlation is defined by
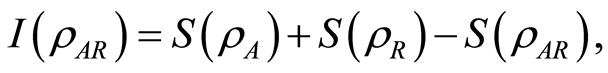 (1)
(1)
where  and
and 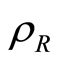 are the local density matrices of
are the local density matrices of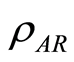 , and
, and 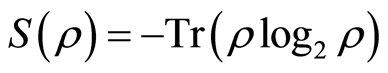 is the von Neumann entropy of a quantum state
is the von Neumann entropy of a quantum state . The classical correlation is [12]
. The classical correlation is [12]
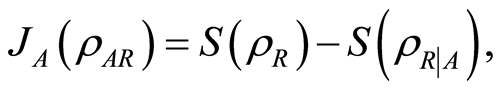 (2)
(2)
where the “quantum conditional entropy” 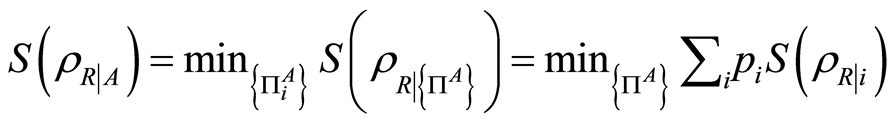 with the minimization being over all projection-valued measurements,
with the minimization being over all projection-valued measurements,  , performed on the subsystem
, performed on the subsystem . The probability for obtaining outcome
. The probability for obtaining outcome  is
is , and the corresponding postmeasurement state for the subsystem
, and the corresponding postmeasurement state for the subsystem  is
is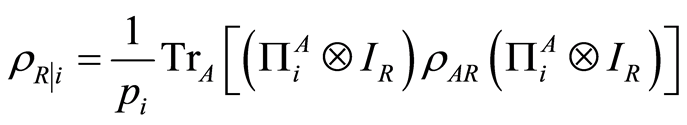 , where
, where 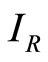 is the identity operator on the Hilbert space
is the identity operator on the Hilbert space .
.
The quantum discord, which aims at capturing all quantum correlations in a state, is the difference 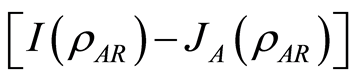 [11] . And for bipartite system with the projective measurement performed on the subsystem A the quantum discord is
[11] . And for bipartite system with the projective measurement performed on the subsystem A the quantum discord is
 (3)
(3)
where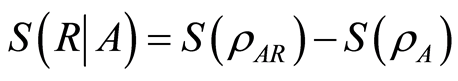 .
.
On the other hand, the geometric discord is a metric-based measure of quantum correlations, which is defined as the distance in state space from the original state to the nearest state with zero discord. Such zero-discord states are known as classical-quantum (quantum-classical) states when the measurement is performed on the subsystem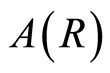 . The geometric discord [16] is given by
. The geometric discord [16] is given by
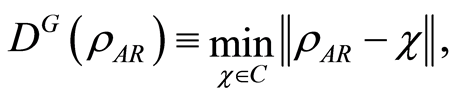 (4)
(4)
where  is the set of classical-quantum states and
is the set of classical-quantum states and 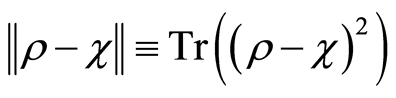 is the squared Hilbert-Schmidt norm. The geometric discord can be expressed as a somewhat more workable form [17]
is the squared Hilbert-Schmidt norm. The geometric discord can be expressed as a somewhat more workable form [17]
 (5)
(5)
where 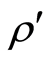 is the state after the projective measurement
is the state after the projective measurement  has been performed on subsystem A, which is given by
has been performed on subsystem A, which is given by 
2.2. Supper Quantum Discord and Inferior “Geometric Discord”
As introduced in Reference [23] , the weak measurement operators are defined as

 (6)
(6)
where  is the parameter that denotes the strength of the measurement process,
is the parameter that denotes the strength of the measurement process, 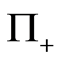 and
and 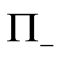 are two orthogonal projectors with
are two orthogonal projectors with 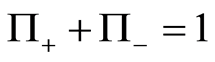 [8] [9] [11] [33] . The weak measurement operators satisfy: 1)
[8] [9] [11] [33] . The weak measurement operators satisfy: 1)
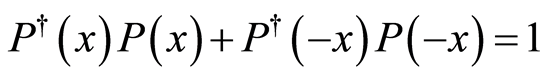 ; 2)
; 2)  results in no change to state; and 3) in the strong measurement limit we can obtain the projective measurement operators, i.e.,
results in no change to state; and 3) in the strong measurement limit we can obtain the projective measurement operators, i.e., 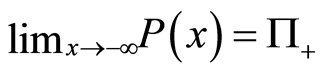 and
and 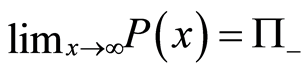 [23] [27] .
[23] [27] .
It is interesting to note that Singh and Pati use the weak measurement, instead of the projective measurement in Equation (3), to define the quantum discord, which they called the super quantum discord [27] due to this quantum discord is always bigger than the normal quantum discord. Doing like defining the normal quantum discord, they assumed that the weak measurement is performed on the subsystem 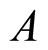 of a state
of a state , then the post-measurement state for the subsystem R is given by
, then the post-measurement state for the subsystem R is given by
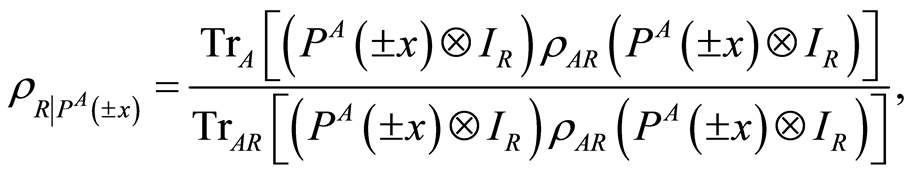 (7)
(7)
where  is weak measurement operators performed on the subsystem
is weak measurement operators performed on the subsystem , and the probability for which is
, and the probability for which is 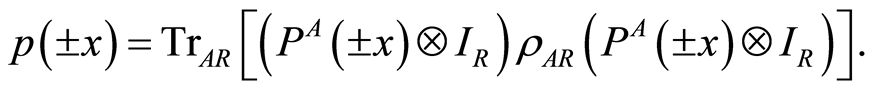
Finally, the super quantum discord is given by
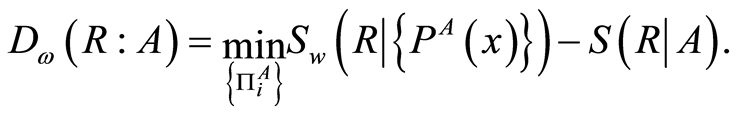 (8)
(8)
where the “weak quantum conditional entropy” is 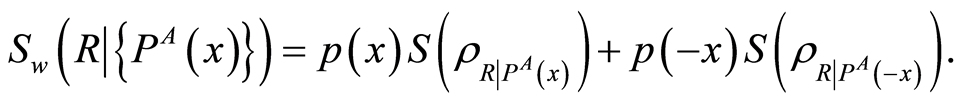
Similarly, we also can define the geometric discord by using the weak measurement to perform on the subsystem  of the state
of the state . After that, the post-measurement state is
. After that, the post-measurement state is
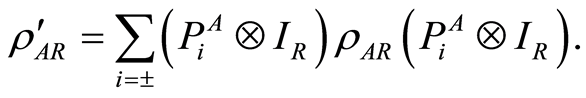 (9)
(9)
Then we can obtain the “geometric discord” based on the weak measurement, which can be expressed as
 (10)
(10)
In the following, we will show this “geometric discord” is always smaller than the normal geometric discord (5), so we call it the inferior “geometric discord”.
3. Quantum Correlations under Weak Measurement in Noninertial Frame
Now, we discuss the super quantum discord and the inferior “geometric discord” in noninertial frame. In order to do that, we first introduce our model that allows us to study the relativistic quantum information.
3.1. Correlated State Shared by Two Relatively Accelerated Observers
We consider that two modes,  and
and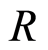 , of a free Dirac field in Minkowski spacetime, are maximally entangled from an inertial perspective, i.e., the quantum field is in a state
, of a free Dirac field in Minkowski spacetime, are maximally entangled from an inertial perspective, i.e., the quantum field is in a state
 (11)
(11)
where  and
and 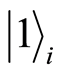 are the vacuum and single particle excitation sates of the mode
are the vacuum and single particle excitation sates of the mode 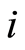 in Minkowski spacetime. We assume that Alice and Rob keep still at the same point in flat Minkowski spacetime at beginning. Then Alice stays stationary while Rob moves with uniform acceleration. Here it is needed to note that Alice has a detector which sensitive only to mode
in Minkowski spacetime. We assume that Alice and Rob keep still at the same point in flat Minkowski spacetime at beginning. Then Alice stays stationary while Rob moves with uniform acceleration. Here it is needed to note that Alice has a detector which sensitive only to mode 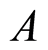 and Rob has a detector sensitive only to mode
and Rob has a detector sensitive only to mode . To correctly describe what Rob sees, mode
. To correctly describe what Rob sees, mode  must be specified in the Rindler coordinates. According to Referece [6] , the Minkowski vacuum
must be specified in the Rindler coordinates. According to Referece [6] , the Minkowski vacuum 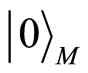 and the one particle state
and the one particle state 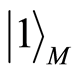 can express with the Rindler basis as follows
can express with the Rindler basis as follows
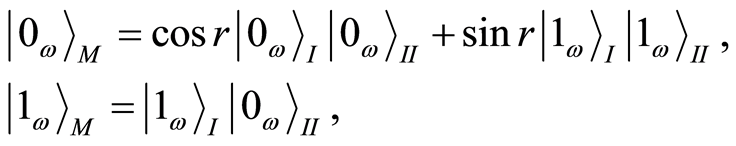 (12)
(12)
where the subscripts  and
and  represent Rindler regions
represent Rindler regions  and
and ,
, 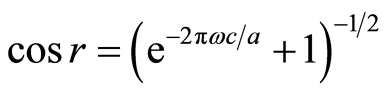 ,
, 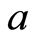 is Rob’s acceleration,
is Rob’s acceleration,  is the frequency of the Dirac particle, and
is the frequency of the Dirac particle, and 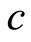 is the speed of light in vacuum. In this regard, let’s note that this model is commonly taken in the literature on relativistic quantum information [3] -[6] [34] [35] .
is the speed of light in vacuum. In this regard, let’s note that this model is commonly taken in the literature on relativistic quantum information [3] -[6] [34] [35] .
Using Equation (12), the state (11) can be rewritten in terms of Minkowski modes for Alice and Rindler modes for Rob. Because the regions 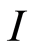 and
and  of Rindler spacetime are causally disconnected, and our accelerated observer Rob is assumed to be in region
of Rindler spacetime are causally disconnected, and our accelerated observer Rob is assumed to be in region , we must trace over the modes in region
, we must trace over the modes in region  where he can’t access. After doing that, the state turns to be
where he can’t access. After doing that, the state turns to be
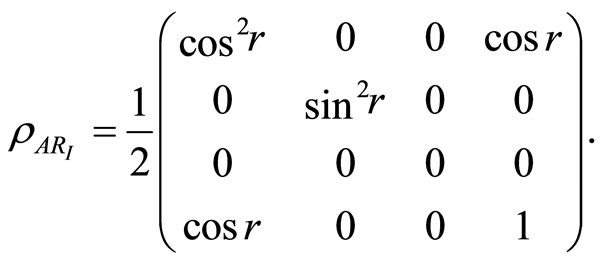 (13)
(13)
Then the von Neumann entropy of the state between Alice and Rob is
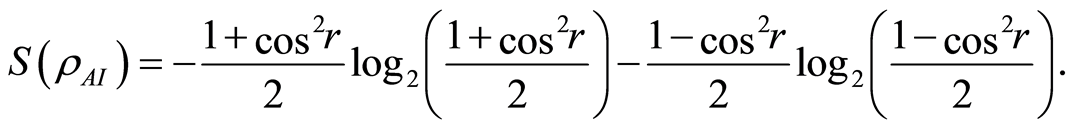 (14)
(14)
And similarly, we can obtain the entropy  for the reduced density matrix
for the reduced density matrix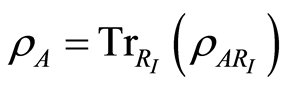 .
.
3.2. Super Quantum Discord
In order to obtain the super quantum discord, the conditional entropy is the key from Equation (8). So, according to Equations (13), the post-measurement state for the subsystem , after the weak measurement
, after the weak measurement 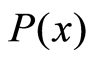 on subsystem
on subsystem  of state (13), is given by
of state (13), is given by
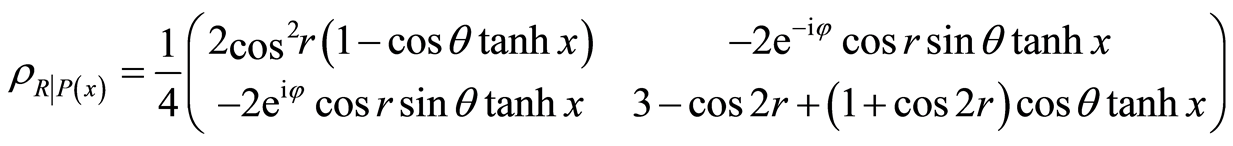 (15)
(15)
with the probability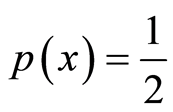 . Similarly, when we change
. Similarly, when we change  to
to  in Equation (15), we can obtain the post-measurement state
in Equation (15), we can obtain the post-measurement state  for the weak measurement
for the weak measurement 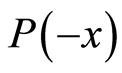 with the probability
with the probability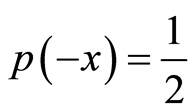 . It is easy to calculate the eigenvalues of the post-measurement states
. It is easy to calculate the eigenvalues of the post-measurement states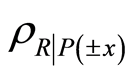 , and then the condition entropy can be obtained. After some calculations, finally the super quantum discord is given by
, and then the condition entropy can be obtained. After some calculations, finally the super quantum discord is given by
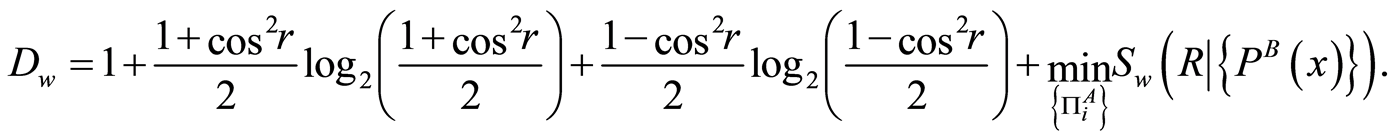 (16)
(16)
We plot the super quantum discord in Figures 1 and 2. From Figure 1 we know that the super quantum discord monotonously decreases as the acceleration increases. And it is the same that with the growing of the measurement strength the super quantum discord decreases monotonously. Besides, the differences between the maximum and the minimum of super quantum discord under the same acceleration become smaller and smaller with the measurement strength increasing. Figure 2 shows that whatever the acceleration is, the super quantum

Figure 1. The super quantum discord (SQD) as a function of the acceleration parameter 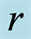 and the parameter of the measurement strength
and the parameter of the measurement strength .
.
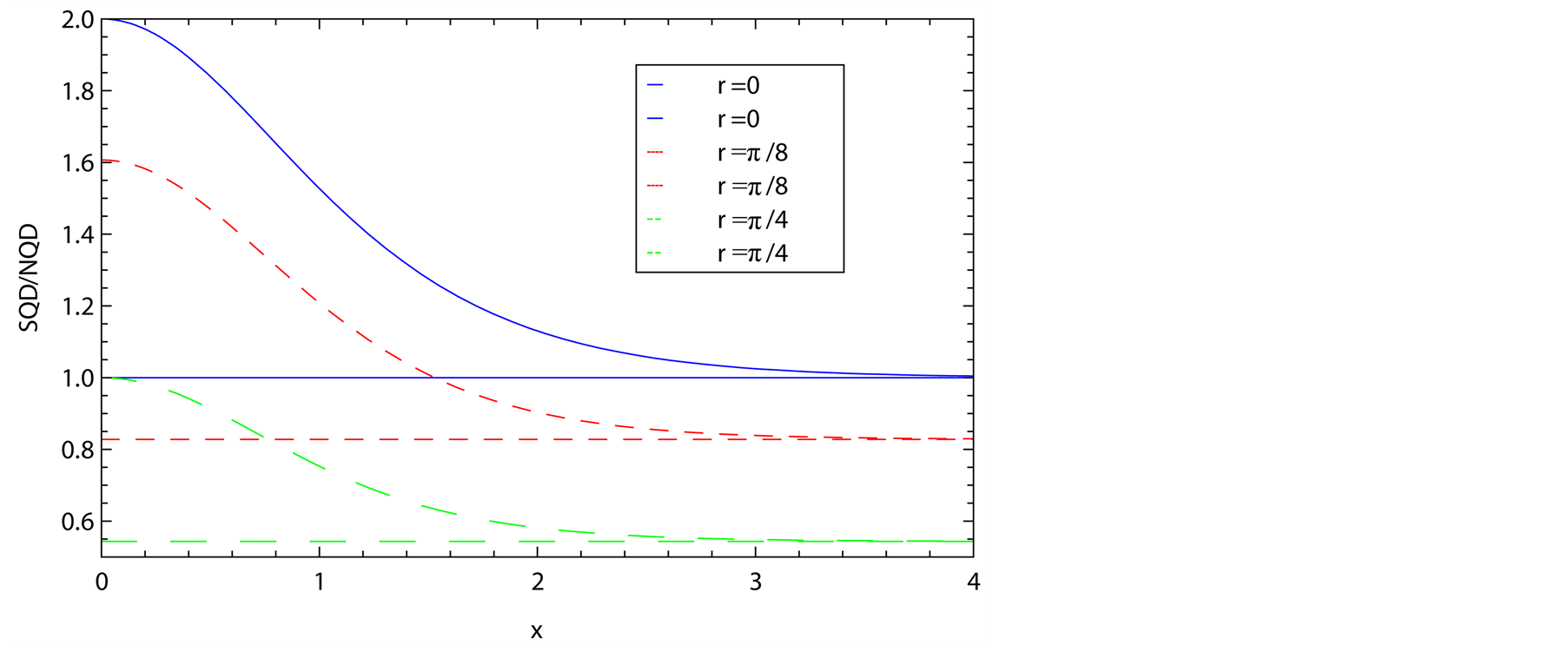
Figure 2. The three curves are the super quantum discords (SQD) as a function of  with some fixed acceleration parameters
with some fixed acceleration parameters  (blue curve),
(blue curve),  (red curve) and
(red curve) and 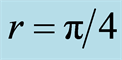 (green curve), and the three straight lines are the normal quantum discords (NQD) as a function of
(green curve), and the three straight lines are the normal quantum discords (NQD) as a function of 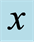 with some fixed acceleration parameters
with some fixed acceleration parameters 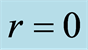 (blue line),
(blue line),  (red line) and
(red line) and 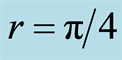 (green line).
(green line).
discord is larger than the normal quantum discord for the weak measurement, but when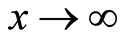 , the super quantum discord approaches to the normal quantum discord. On the other hand, by changing the acceleration, we can not change the trend that the super quantum discord decreases with the measurement strength increasing, but just decay the values of the super quantum discord and the difference between the maximum and the minimum of super quantum discord.
, the super quantum discord approaches to the normal quantum discord. On the other hand, by changing the acceleration, we can not change the trend that the super quantum discord decreases with the measurement strength increasing, but just decay the values of the super quantum discord and the difference between the maximum and the minimum of super quantum discord.
3.3. Inferior “Geometric Discord”
Let’s consider the “geometric discord” based on the weak measurement of the sate (13) shared by Alice and the accelerated Rob. The state after the weak measurement performed on the subsystem  can be calculated by using Equation (9) as
can be calculated by using Equation (9) as
 (17)
(17)
where

Then, according to Equation (10), after some calculations we can finally obtain the “geometric discord” based on the weak measurement as following
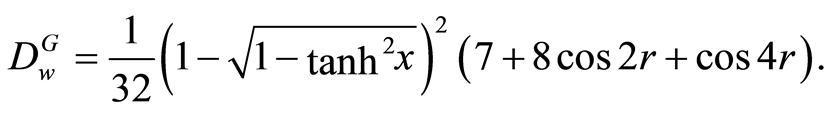 (18)
(18)
Obviously, Equation (18) will go back to the normal geometric discord [18] when 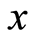 approaches to the infinite, i.e.,
approaches to the infinite, i.e.,
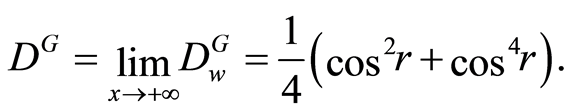 (19)
(19)
It is interesting to note that the “geometric discord” based on the weak measurement is always smaller than or equal to the normal geometric discord. This property of the inferior “geometric discord” is distinctly different from that of the super quantum discord, so this may be an evidence to prove that the definitions of the quantum discord and geometric discord are not too concordant with each other [21] .
We plot the inferior “geometric discord” as a function of the parameterized acceleration 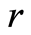 and measurement strength
and measurement strength 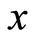 in Figures 3 and 4. From Figure 3, we know that the inferior “geometric discord” decreases with the acceleration increasing, but it increases as the measurement strength increases. Furthermore, the inferior “geometric discord” vanishes when
in Figures 3 and 4. From Figure 3, we know that the inferior “geometric discord” decreases with the acceleration increasing, but it increases as the measurement strength increases. Furthermore, the inferior “geometric discord” vanishes when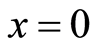 . It is shown in Figure 4 that the inferior “geometric discord” grows with the increase of the measurement strength, and it is always smaller than the normal geometric discord when the parameter of the measurement strength
. It is shown in Figure 4 that the inferior “geometric discord” grows with the increase of the measurement strength, and it is always smaller than the normal geometric discord when the parameter of the measurement strength 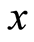 is not equal to
is not equal to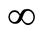 .
.

Figure 3. The inferior “geometric discords” (IGD) as a function of the acceleration parameter  and the parameter of the measurement strength
and the parameter of the measurement strength .
.

Figure 4. The three curves are the inferior “geometric discords” (IGD) as a function of 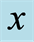 with some fixed acceleration parameters
with some fixed acceleration parameters  (blue curve),
(blue curve),  (red curve) and
(red curve) and  (green curve), and the three straight lines are the normal geometric discords (NGD) as a function of
(green curve), and the three straight lines are the normal geometric discords (NGD) as a function of 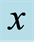 with some fixed acceleration parameters
with some fixed acceleration parameters  (blue line),
(blue line),  (red line) and
(red line) and  (green line).
(green line).
4. Summary and Discussions
By investigating the quantum correlations based on the weak measurement in noninertial frame we study the properties and inconsistence of the quantum discord and geometric discord. We find that: 1) using the weak measurement to define the quantum discord we can capture more quantum correlations and obtain a super quantum discord. However, using the weak measurement to define the geometric discord we note that the quantity becomes smaller and results in a inferior “geometric discord”; 2) with the increase of the observer’s acceleration, both the super quantum discord and the inferior “geometric discord” decrease monotonously; and 3) as the measurement strength increases, the super quantum discord decreases monotonously, and finally goes back to the normal quantum discord when the strength parameter, 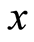 , approaches to the infinity. However, the inferior “geometric discord” increases with the increase of the measurement strength, also goes back to the normal geometric discord when
, approaches to the infinity. However, the inferior “geometric discord” increases with the increase of the measurement strength, also goes back to the normal geometric discord when . Different properties of the quantum and the geometric discords based on the weak measurement show us that these two “discords” have completely different reactions to the change of the measurement strength. So, in some sense, we can say that these differences are the evidences to prove the inconsistence between the quantum discord and the geometric discord.
. Different properties of the quantum and the geometric discords based on the weak measurement show us that these two “discords” have completely different reactions to the change of the measurement strength. So, in some sense, we can say that these differences are the evidences to prove the inconsistence between the quantum discord and the geometric discord.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11175065, 10935013; the National Basic Research of China under Grant No. 2010CB833004; the SRFDP under Grant No. 20114306110003; the Hunan Provincial Natural Science Foundation of China under Grant No 11JJ7001; and Construct Program of the National Key Discipline.
References
- Peres, A. and Terno, D.R. (2004) Quantum Information and Relativity Theory. Reviews of Modern Physics, 76, 93- 123. http://dx.doi.org/10.1103/RevModPhys.76.93
- Bouwmeester, D., Ekert, A. and Zeilinger, A. (2000) The Physics of Quantum Information. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-04209-0
- Alsing, P.M. and Milburn, G.J. (2003) Teleportation with a Uniformly Accelerated Partner. Physical Review Letters, 91, Article ID: 180404. http://dx.doi.org/10.1103/PhysRevLett.91.180404
- Fuentes-Schuller, I. and Mann, R.B. (2005) Alice Falls into a Black Hole: Entanglement in Noninertial Frames. Physical Review Letters, 95, Article ID: 120404. http://dx.doi.org/10.1103/PhysRevLett.95.120404
- Pan, Q. and Jing, J. (2008) Degradation of Nonmaximal Entanglement of Scalar and Dirac Fields in Noninertial Frames. Physical Review A, 77, Article ID: 024302.
- Alsing, P.M., Fuentes-Schuller, I., Mann, R.B. and Tessier, T.E. (2006) Entanglement of Dirac Fields in Noninertial Frames. Physical Review A, 74, Article ID: 032326. http://dx.doi.org/10.1103/PhysRevA.74.032326
- Bruschi, D.E., Louko, J., Martn-Martnez, E., Dragan, A. and Fuentes, I. (2010) Unruh Effect in Quantum Information beyond the Single-Mode Approximation. Physical Review A, 82, Article ID: 042332. http://dx.doi.org/10.1103/PhysRevA.82.042332
- Datta, A., Flammia, S.T. and Caves, C.M. (2005) Entanglement and the Power of One Qubit. Physical Review A, 72, Article ID: 042316. http://dx.doi.org/10.1103/PhysRevA.72.042316
- Datta, A., Shaji, A. and Caves, C.M. (2008) Quantum Discord and the Power of One Qubit. Physical Review Letters, 100, Article ID: 050502. http://dx.doi.org/10.1103/PhysRevLett.100.050502
- Lanyon, B.P., Barbieri, M., Almeida, M.P. and White, A.G. (2008) Experimental Quantum Computing without Entanglement. Physical Review Letters, 101, Article ID: 200501. http://dx.doi.org/10.1103/PhysRevLett.101.200501
- Ollivier, H. and Zurek, W.H. (2001) Quantum Discord: A Measure of the Quantumness of Correlations. Physical Review Letters, 88, Article ID: 017901. http://dx.doi.org/10.1103/PhysRevLett.88.017901
- Henderson, L. and Vedral, V. (2001) Classical, Quantum and Total Correlations. Journal of Physics A: Mathematical and General, 34, 6899. http://dx.doi.org/10.1088/0305-4470/34/35/315
- Zurek, W.H. (2003) Quantum Discord and Maxwell’s Demons. Physical Review A, 67, Article ID: 012320. http://dx.doi.org/10.1103/PhysRevA.67.012320
- Datta, A. (2009) Quantum Discord between Relatively Accelerated Observers. Physical Review A, 80, Article ID: 052304. http://dx.doi.org/10.1103/PhysRevA.80.052304
- Wang, J., Deng, J. and Jing, J. (2010) Classical Correlation and Quantum Discord Sharing of Dirac Fields in Noninertial Frames. Physical Review A, 81, Article ID: 052120. http://dx.doi.org/10.1103/PhysRevA.81.052120
- Dakić, B., Vedral, V. andBrukner, C. (2010) Necessary and Sufficient Condition for Nonzero Quantum Discord. Physical Review Letters, 105, Article ID: 190502. http://dx.doi.org/10.1103/PhysRevLett.105.190502
- Luo, S. and Fu, S. (2010) Geometric Measure of Quantum Discord. Physical Review A, 82, Article ID: 034302. http://dx.doi.org/10.1103/PhysRevA.82.034302
- Brown, E.G., Cormier, K., Martin-Martinez, E. and Mann, R.B. (2012) Vanishing Geometric Discord in Noninertial Frames. Physical Review A, 86, Article ID: 032108. http://dx.doi.org/10.1103/PhysRevA.86.032108
- Tian, Z. and Jing, J. (2013) Measurement-Induced-Nonlocality via the Unruh Effect. Annals of Physics, 333, 76. http://dx.doi.org/10.1016/j.aop.2013.02.001
- Okrasa, M. and Walczak, Z. (2012) On Two-Qubit States Ordering with Quantum Discords. EPL (Europhysics Letters), 98, 40003. http://dx.doi.org/10.1209/0295-5075/98/40003
- Piani, M. (2012) Problem with Geometric Discord. Physical Review A, 86, Article ID: 034101. http://dx.doi.org/10.1103/PhysRevA.86.034101
- Aharonov, Y., Albert, D.Z. and Vaidman, L. (1988) How the Result of a Measurement of a Component of the Spin of a Spin-1/2 Particle Can Turn out to Be 100. Physical Review Letters, 60, 1351. http://dx.doi.org/10.1103/PhysRevLett.60.1351
- Oreshkov, O. and Brun, T.A. (2005) Weak Measurements Are Universal. Physical Review Letters, 95, Article ID: 110409. http://dx.doi.org/10.1103/PhysRevLett.95.110409
- Hosten, O. and Kwiat, P. (2008) Observation of the Spin Hall Effect of Light via Weak Measurements. Science, 319, 787. http://dx.doi.org/10.1126/science.1152697
- Lundeen, J.S., Sutherland, B., Patel, A., Stewart, C. and Bamber, C. (2011) Direct Measurement of the Quantum Wavefunction. Nature, 474, 188. http://dx.doi.org/10.1038/nature10120
- Sjöqvist, E. (2006) Geometric Phase in Weak Measurements. Physics Letters A, 359, 187-189. http://dx.doi.org/10.1016/j.physleta.2006.06.028
- Singh, U. and Pati, A. (2012) Super Quantum Discord with Weak Measurements. arXiv:1211.0939
- Singh, U. and Pati, A. (2013) Weak Measurement Induced Super Discord Can Resurrect Lost Quantumness. arXiv:1305.4393
- Wang, Y., Ma, T., Fan, H., Fei, S. and Wang, Z. (2014) Super-Quantum Correlation and Geometry for Bell-Diagonal States with Weak Measurements. Quantum Information Process, 13, 283.
- Li, B., Chen, L., Fan, H., Fei, S.M. and Wang, Z.X. (2013) Necessary and Sufficient Condition for Vanishing Super Discord. arXiv:1301.7500
- Huai, L., Li, B., Gu, M., Qu, S. and Fan, H. (2013) Quantum Advantage by Weak Measurements. arXiv:1305.6366
- Hu, M., Fan, H. and Tian, D. (2013) Dual Role of Weak Measurements for Quantum Correlation. arXiv:1304.5074
- Wang, J., Deng, J. and Jing, J. (2010) Classical Correlation and Quantum Discord Sharing of Dirac Fields in Noninertial Frames. Physical Review A, 81, Article ID: 052120. http://dx.doi.org/10.1103/PhysRevA.81.052120
- Martin-Martinez, E., Garay, L.J. and Leon, J. (2010) Unveiling Quantum Entanglement Degradation near a Schwarzschild Black Hole. Physical Review D, 82, Article ID: 064006.
NOTES

*Corresponding author.

